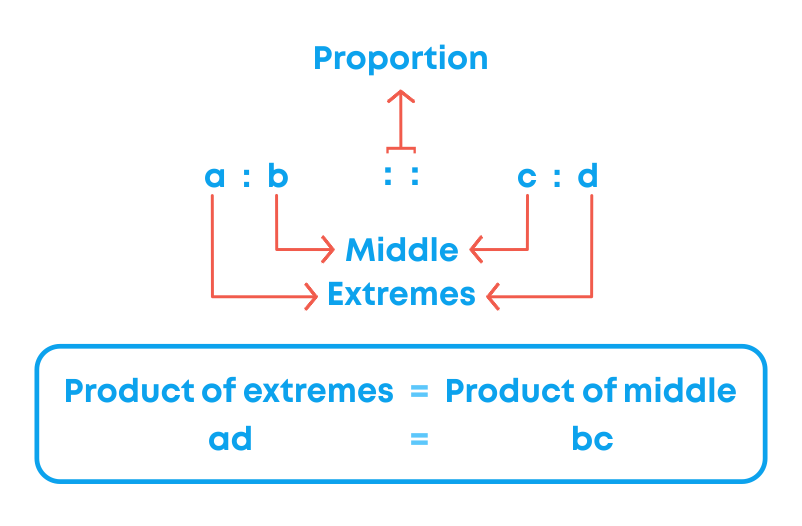
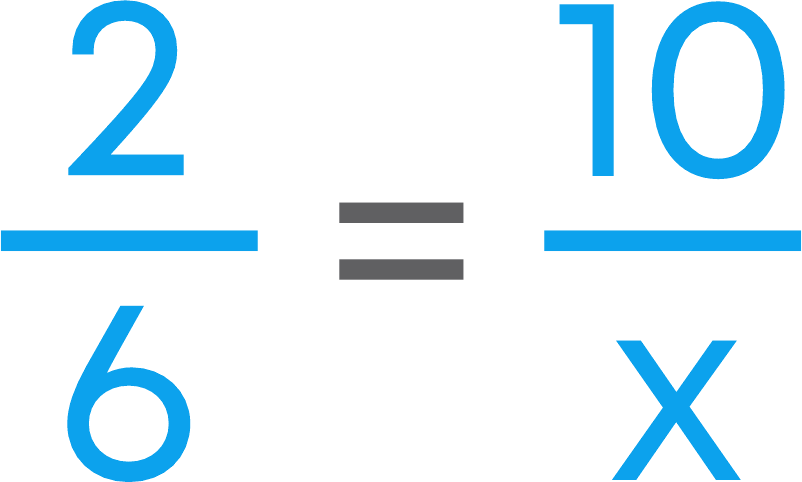Introduction

We all come across various shapes in our life, which includes rectangles, squares, triangles, and a lot more. But a very important question arises that how do we measure these shapes? What are their lengths, width, and what area do they occupy?

Watch the video below to know more.

What have we learned from the video?

Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.

The idea of perimeter is used in daily lives when:

  • A farmer wants to fence his field.
  • An engineer plans to build a compound wall on all sides of his house.
  • A person is preparing a track to conduct sports.

The amount of surface enclosed by a closed figure is called its area.

We often find the area of:

  • Our room floor to determine the size of the carpet to be bought.
  • Our floor to buy tiles for the room.
  • The wall to paint or put a wallpaper.

Can you think of some activities that you have done where you used mensuration? Think of the times you required to know the total perimeter or surface areas of objects.

When painting a wall or even a large sheet of paper, you roughly calculate how much paint you require by finding out the surface area to be covered. Or, when gardening, you notice that the gardener will measure how much soil is to be filled in a hole by finding out the volume of the hole which is dug up.

Concepts

The chapter ‘Mensuration’ covers the following concepts:

Perimeter Area

Perimeter

Perimeter is the total length or total distance covered along the boundary of a closed shape. Let us take an example:

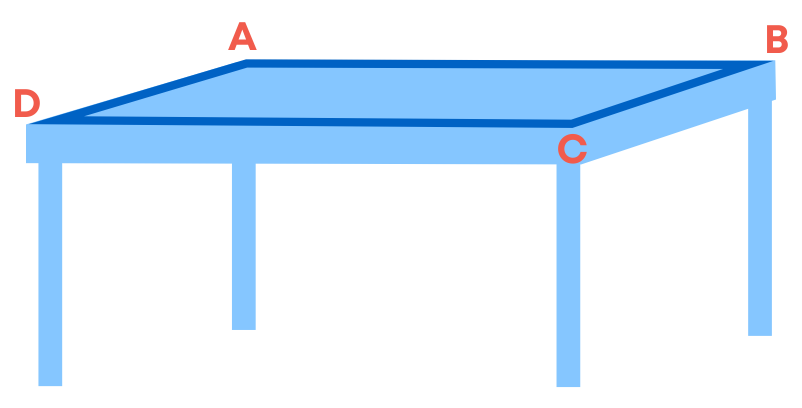
The perimeter of the top of the table will be the distance covered along the boundary, that is the sum of the length of four sides. So, how will you find the perimeter of any closed figure made up entirely of line segments? Simply find the sum of the lengths of all the sides (which are line segments).

If a figure is made up of only line segments, we can find its perimeter by adding the length of all the sides of the given figure.

Perimeter of a closed figure = sum of the lengths of all sides

Since the perimeter is the length or distance, the unit of measurement is inch, feet, mile, centimetre, metre, kilometre etc. If all the measurements are in centimetre, the units of measurement for the perimeter of shapes will also be in centimetre. Similarly, if the measurements of all sides are in metres, the units of measurement for the perimeter of different shapes will also be in metres.

In general, two main systems of measurements are used:

  • Metric system
  • Imperial units

To measure smaller lengths such as the height of a person, the length of a pencil etc., we use centimetre, foot, or inch.

To measure the length of a room or length of a backyard we use metre or yard.

To measure large distances such distance between two cities we use kilometre.

You know that a rectangle is a four-sided polygon in which the opposite sides are parallel and equal to each other.

Perimeter of the rectangle = 2 × (length + breadth)

To solve real-life problems using the perimeter of a rectangle, follow the steps as given below:

  • Analyse the question to find what is given and what is to be found..
  • Write down the formula of the perimeter of the rectangle.
  • Substitute the given values and find the perimeter.
  • Make sure the units used are the same for all the dimensions.

You can also find the length/ breadth of a rectangle when the perimeter is given.

Length = perimeter / 2 - Breadth

Breadth = perimeter / 2 - Length

Rahul travels 5 km daily to go to school and from the school he travels 8 km to go to his tuition class. He then finally travels 6 km to reach his home. Let us map his route:

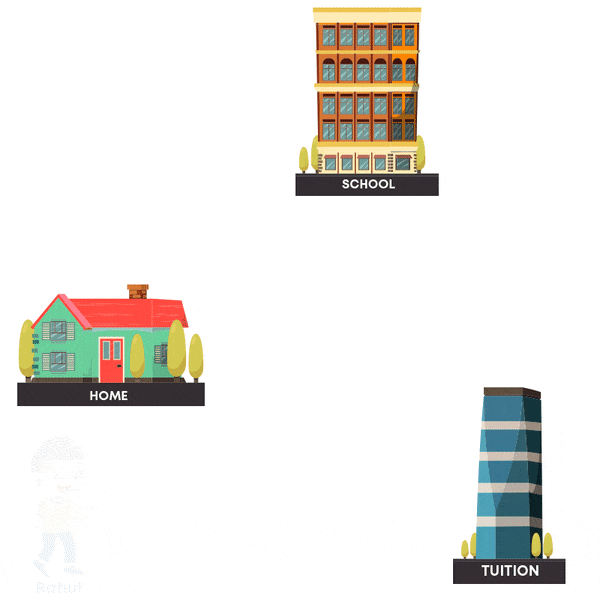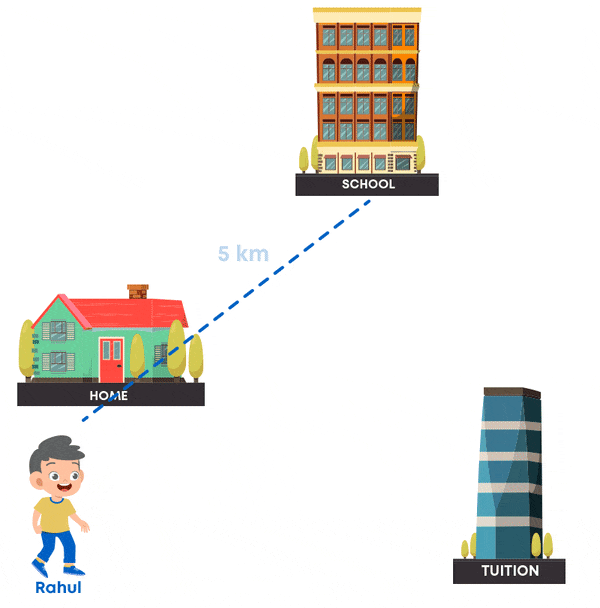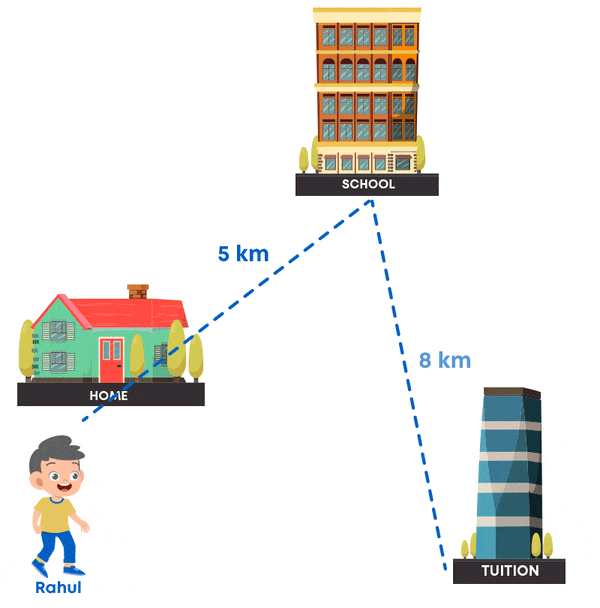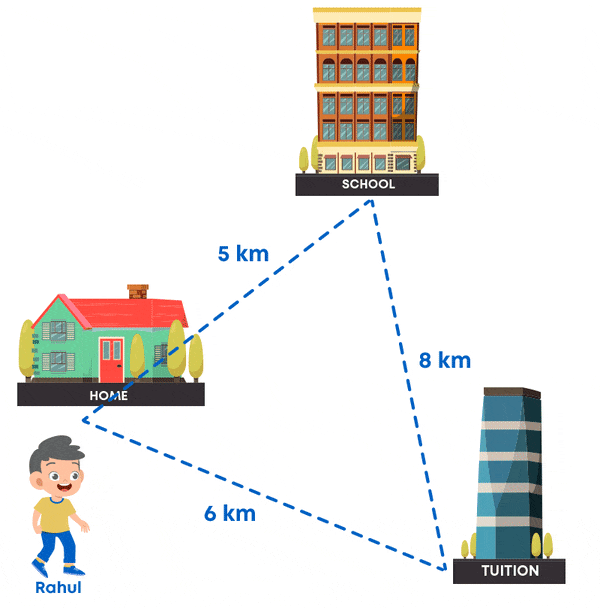
How much has he travelled in total? For this, we must add 5 km, 8 km and 6 km, which is nothing but the perimeter of a triangle. So, Rahul has travelled 19 km in total.

If the length of the sides of a triangle are ‘a’, ‘b’ and ‘c’ units, it’s perimeter will be:

Side + side + side = (a + b + c) units

​

An isosceles triangle has two sides equal, hence, its perimeter = sum of two equal sides + unequal side.

If the perimeter and two sides of a triangle are given, then the missing side can be calculated by subtracting the sum of the two sides from the perimeter.

A polygon that does not have all sides equal and all angles equal is known as 'Irregular Polygon'.

A regular polygon is one where all the sides are equal, and all the angles are equal.

For a regular polygon, the perimeter of the polygon will be the product of the length of its side and the number of sides.

Perimeter of a regular polygon = length of one side x number of sides

  • Perimeter of an equilateral triangle = 3 × length of a side
  • Perimeter of a square = 4 × length of a side
  • Perimeter of a regular pentagon = 5 × length of a side
  • Perimeter of a regular hexagon = 6 × length of a side

Gaurav wants to buy wood to put a frame around his photograph. Each side of his photo is 20 cm. What is the length of wood frame he should buy?

Here, we must calculate the total length of the photograph. Hence, we will need to calculate the perimeter of the shape.

Perimeter = 4 × length of one side

= 4 × 20 cm

= 80 cm

Hence, Gaurav should buy 80 cm of wood frame.

We know that the perimeter of a regular polygon = number of sides × length of one side

Therefore, the length of one side = perimeter ÷ number of sides

Area

You know that the amount of surface enclosed by a closed figure is called its area. A square is used as a unit of measurement of area. When we compare areas, we need to measure all the figures with squares of the same size. Generally, a unit square is used as a unit of measurement for measuring area. For e.g., sq. m and sq. cm.

All closed figures, such as circles, triangles, squares, rectangles, have an area. For every closed figure, there are two regions, the interior and exterior region.

The term ‘area’ refers to the measure of the total interior region.

On a graph paper or squared paper, the area of one full square is taken as 1 sq. unit. If it is a centimetre square sheet, then the area of one full square will be 1 sq. cm. Ignore portions of the area that are less than half a square. If more than half of a square is in a region, just count it as one square. ​If exactly half the square is counted, take its area as 12 sq. unit.

​Observe this rectangle with length 4 cm and breadth 3 cm.

The rectangle covers 12 squares completely. The area of the rectangle = 12 sq. cm, which can be written as 4 × 3 sq. cm. i.e. (length × breadth).

What do we infer from this?

Area of a rectangle = (length × breadth)

Now, try solving this real-life problem:

What is the cost of tiling a rectangular plot of land which is 500 m long and 200 m wide at the rate of ₹10 per hundred sq. m.?

Area of the land = length × breadth
= 500 m × 200 m
= 1,00,000 sq. m
∴ Cost of tiling 1,00,000 sq. m of land
= (10 × 1,00,000) ÷ 100
= ₹10,000

Therefore, the total cost of tiling the plot will be ₹10,000.

Remember, cost of levelling/tiling = area × cost per unit square

We can also find length or breadth of a rectangle when area and one side is given.

Breadth of a rectangle = area of rectang / lelength of rectangle

Length of a rectangle = area of rectangle / breadth of rectangle

Similarly, area of a square = side × side

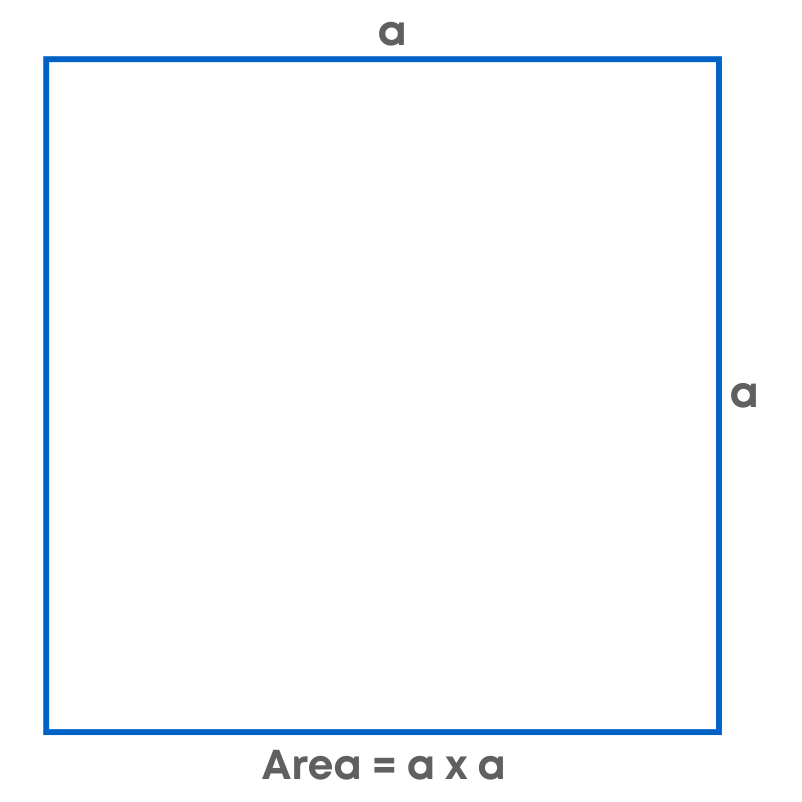
When area is given, think of a number which when multiplied twice to it gives the same number. E.g., if the area is 16 sq. m, then the side of the square will be 4 m, because 4 × 4 = 16.

We have seen certain figures which are a combination of shapes, such as squares and rectangles. To find the area by splitting the figure into squares:

  • Step 1: Split the shapes into squares.
  • Step 2: Write the measurements for each square.
  • Step 3: Find the area of each square.
  • Step 4: Add the areas of all the squares. The sum of the areas of all the squares gives the area of the figure.

Follow the same process for rectangle figures. For example, by splitting the following figure into rectangles, find its area (The measures are given in centimetres).

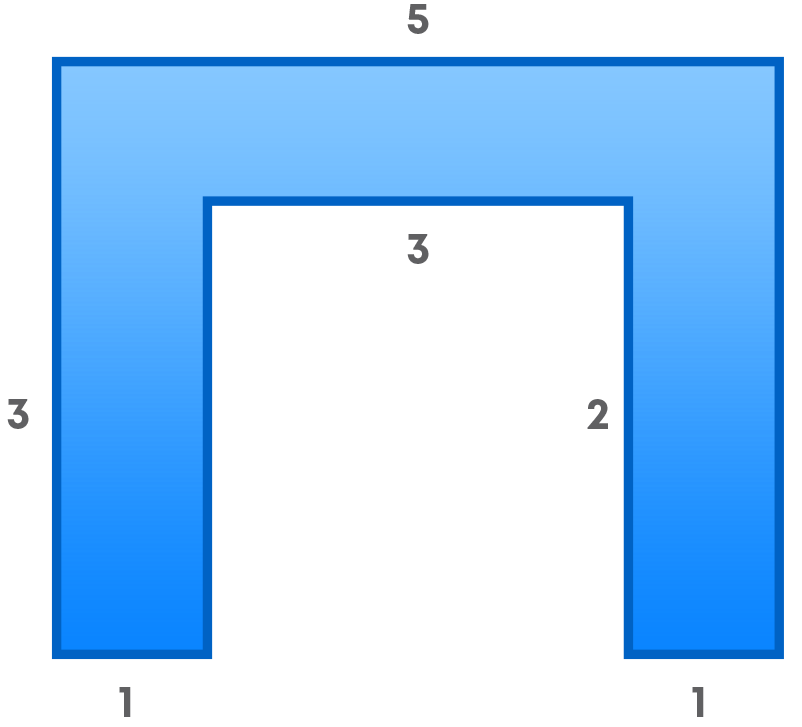
We can split the following figure into 3 rectangles as shown below:

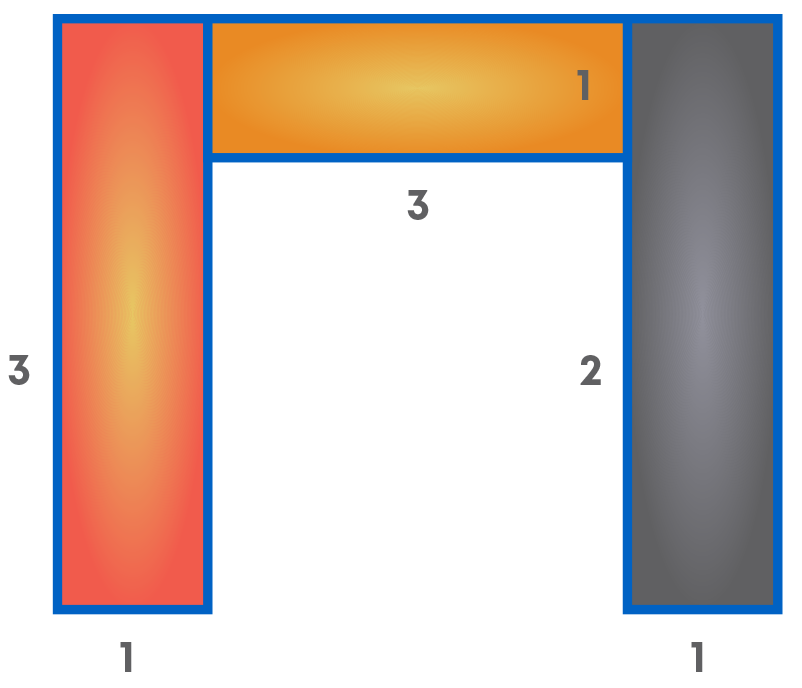
Area of the yellow rectangle = 3 × 1

= 3 sq. cm.

Area of the orange rectangle = 3 × 1

= 3 sq. cm.

Area of the black rectangle = 3 × 1

= 3 sq. cm.

Total area = 3 + 3 + 3

= 9 sq. cm.

Therefore, the total area is 9 sq. cm.

Common Errors

The following are the topics in which students make common mistakes when dealing with mensuration:

  • 1.Difference between perimeter and area
  • 2.Context where we calculate perimeter and area
  • 3.Remember the units
  • 4.Check the units

Difference Between Perimeter And Area

Sometimes we get confused between perimeter and area. We may think of the area as perimeter and perimeter as area. But remember,

Perimeter refers to the length of the outline of the enclosed figure and area refers to the surface of the enclosed figure.

Context Where We Calculate Perimeter And Area

Let us see situations where we use perimeter and area in daily life.

What did you observe in the examples above?

  • The cost of framing or fencing a land is calculated by finding its perimeter.
  • The cost of painting a surface depends on the area of the surface.

Remember The Units

Observe the examples given below:

  • Find the perimeter of the given figure.

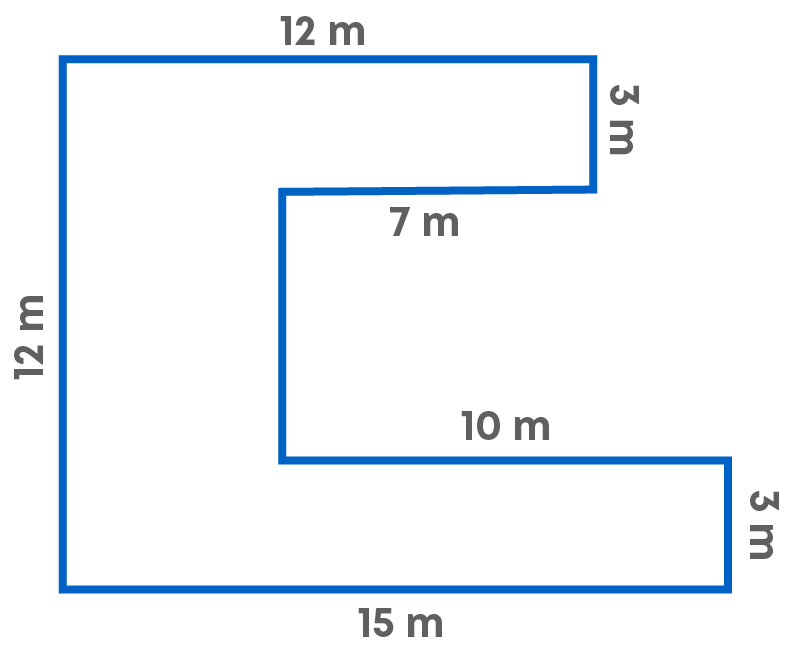
Response 1:

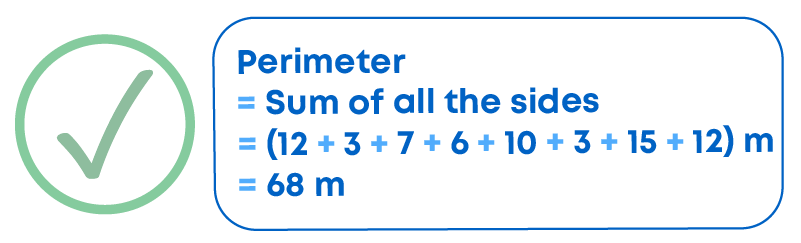
Response 2:

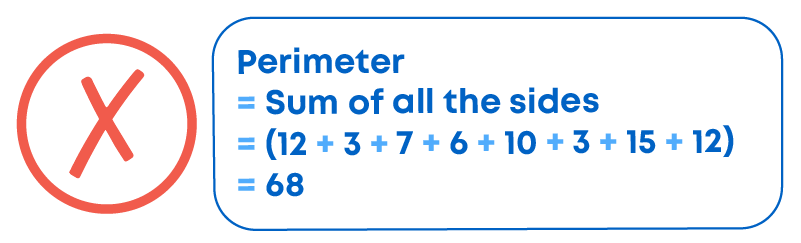
Why is the second response wrong?

Because while writing the perimeter, the unit ‘metre’ was missed. Always remember to write the units at the end, which should be the same for all given sides.

  • Find the area of a rectangle whose length and breadth are 20 cm and 12 cm respectively.

Response 1:

Response 2:

Did you notice the difference between the two responses? Yes! In the first response, the unit is cm2 whereas in the second response, the unit is cm.

Remember: Area is always measured in square units.

Check The Units

Observe the examples given below:

Find the area of a rectangular field whose length is 3 m and breadth is 250 cm respectively.

Response 1:

Response 2:

Did you notice the difference between the two responses? Yes! In the first response, the unit is different whereas in the second response, we first converted cm to m so that units of both dimensions are same.

Remember: Always check that the given dimensions have the same units. If not, convert either one.

Conclusion

You have learnt how to solve real-life problems based on shapes and their perimeter and area. What can you say about the given rectangles?

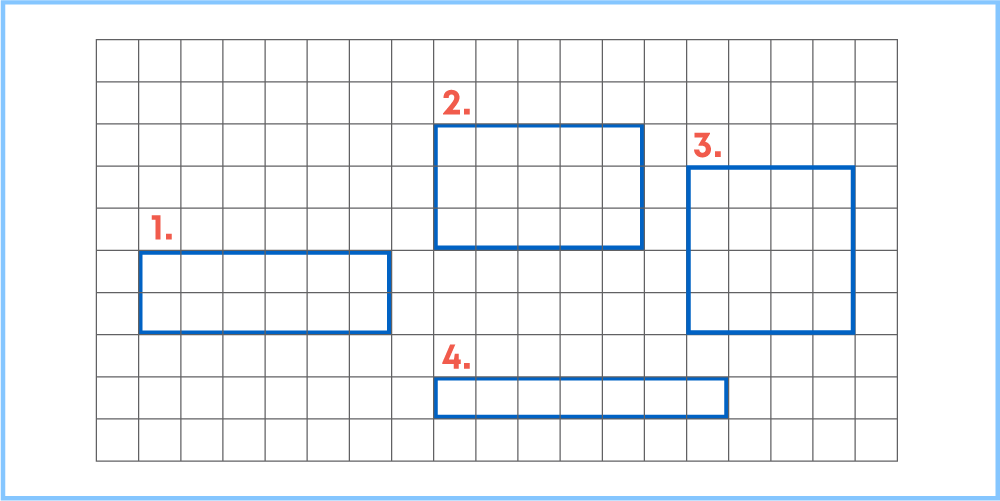
Options:

  • 1. All rectangles have same perimeter but different area
  • 2. All rectangles have same area but different perimeter
  • 3. All rectangles have same area and same perimeter
  • 4. All rectangles have different area and different perimeter

Jyothi

Author

A math enthusiast and an educationist, Jyothi has a strong academic background and has demonstrated an impressive history of working in the education industry. Jyothi is skilled in developing and reviewing lesson plans, learning content, assessments, and video story boards and scripts.