Introduction
We find symmetry in many objects around us. Let us watch this video to know more about symmetry and its applications.
Symmetry is found everywhere and in nature we find abundant symmetry.


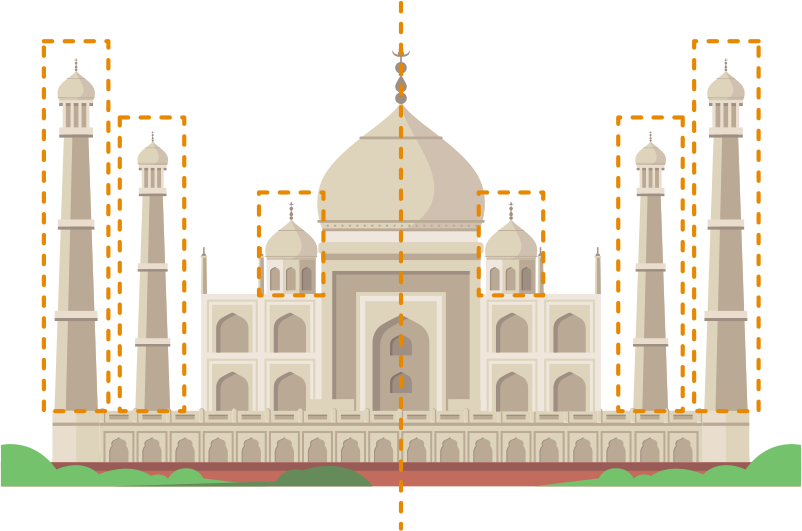
Symmetry is also commonly used in architecture by architects to build complex designs. A famous example of symmetry in architecture is the Taj Mahal.

Do you notice that the left side of the image is the same as the right side? This is because the Taj Mahal was built keeping symmetry in mind.
Concepts
The chapter ‘Symmetry’ covers the following concepts:
Lines of Symmetry for Regular Polygons
Observe the shapes given below:


Let us divide these shapes into two halves.
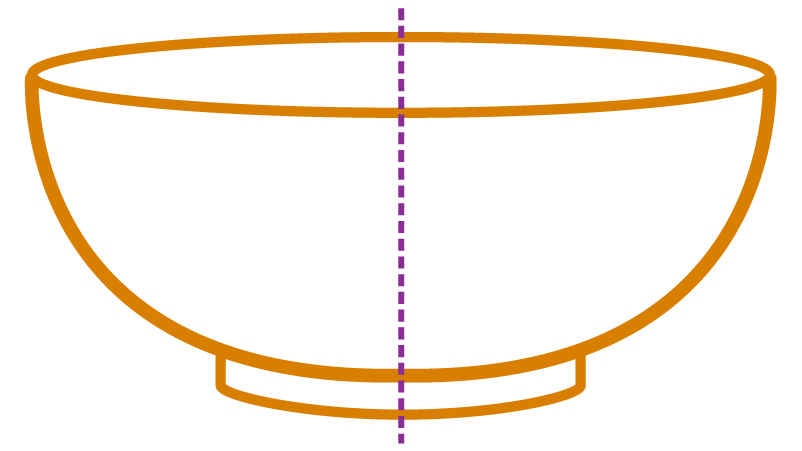

Are the two halves exactly the same? Can we say they are symmetrical? Yes, the shapes you see here are symmetrical. Why? When you fold them along the dotted line, each point of the first half will coincide exactly with each point of the second half.

This dotted line is called the line of symmetry. Line of symmetry is also called the axis of symmetry.
Line of symmetry is a line which divides an object or figure into two halves such that the first half will coincide with the second half.
Observe the following objects:


These objects can be divided into half, vertically in such a way that the two halves match exactly.
So, these objects have a line of symmetry.

Figures/ objects having line/lines of symmetry are called symmetric figures/objects.
Now look at the following objects:


These objects can be divided into half but the two halves do not match exactly.
So, these objects do not have any line of symmetry.

Figures/objects having no line of symmetry are called asymmetric figures/objects.
Observe the dotted lines shown below for the same object:

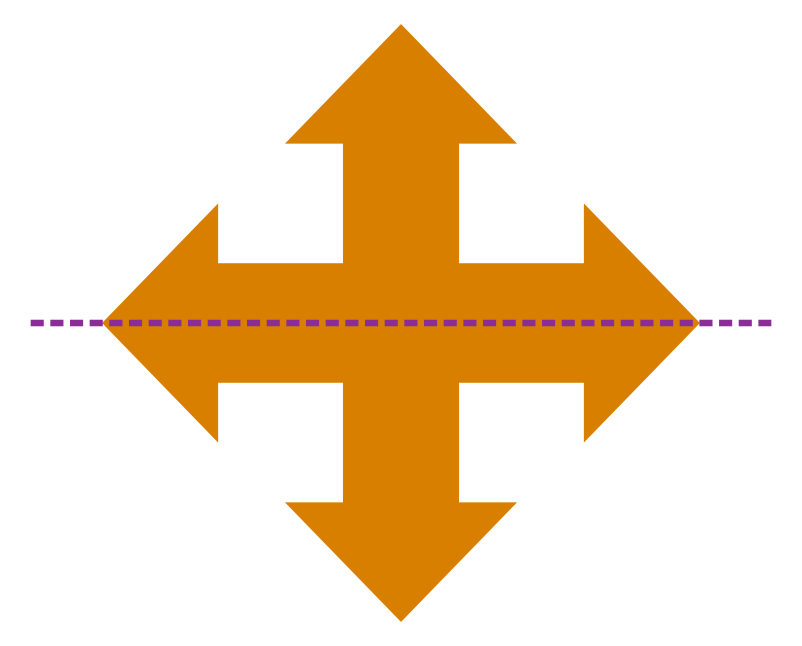
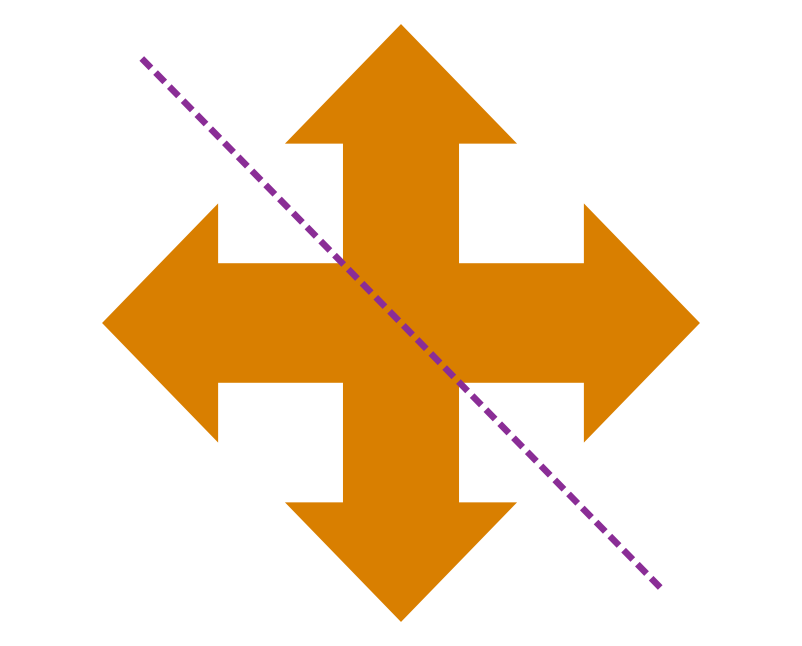

We can say that each of these dotted lines divides the object into two halves such that first half coincides with the second half. So, the number of lines of symmetry for this object is 4.
Hence, an object can have more than one line of symmetry.
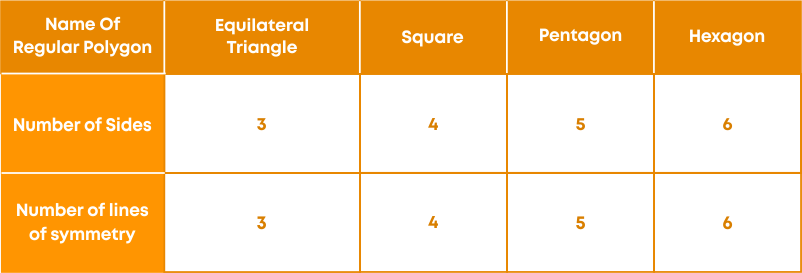
A polygon is a closed figure made of several line segments. A polygon is said to be regular if all its sides are of equal lengths and all its angles are of equal measure. Let us see the different types of polygons:
A regular polygon of three sides is an equilateral triangle.

A regular polygon of four sides is a square.

A regular polygon of five sides is a regular pentagon.

A regular polygon of six sides is a regular hexagon.

Observe the figures given below:
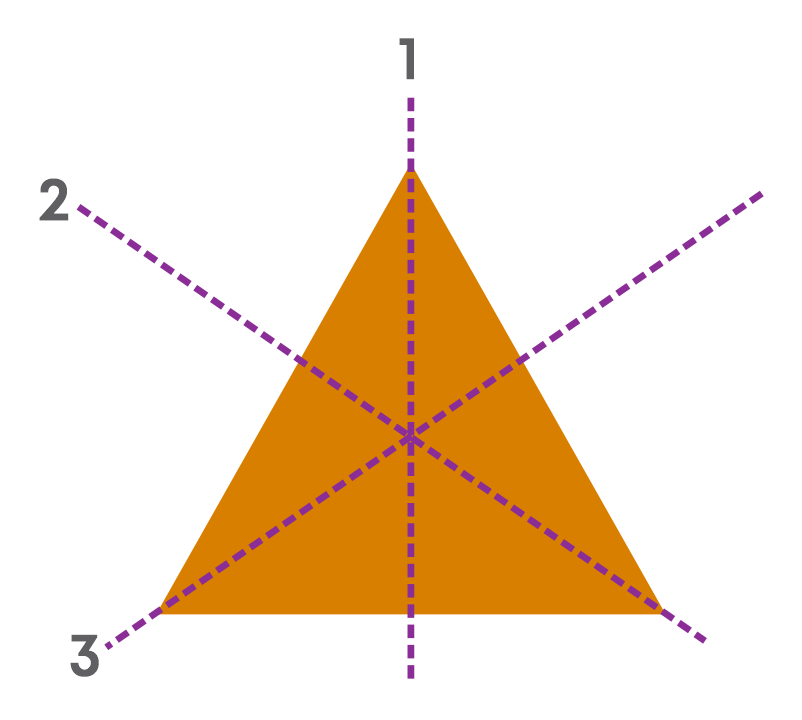
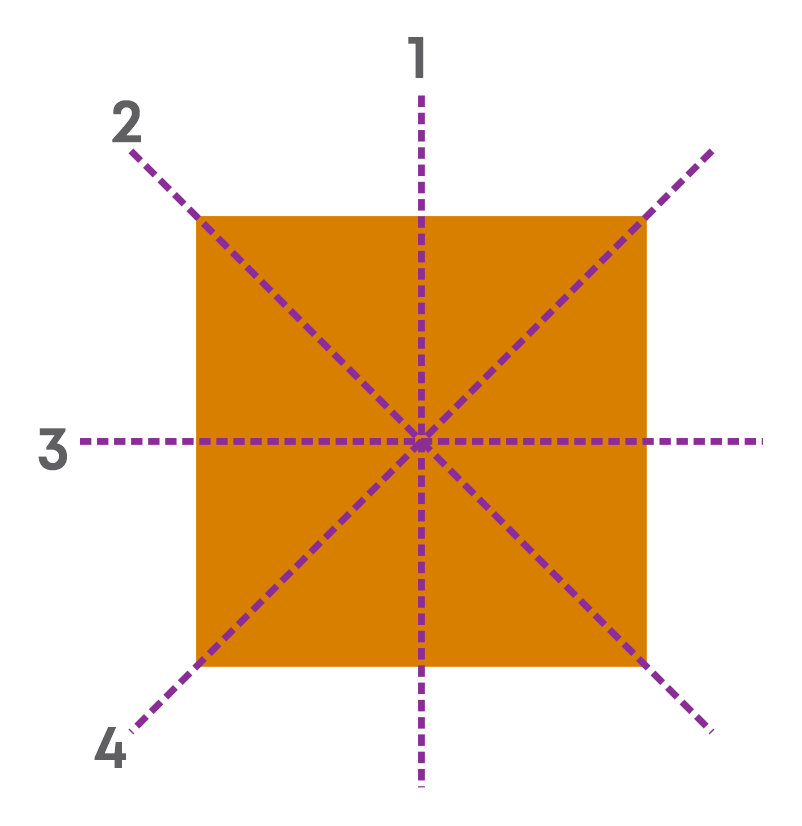
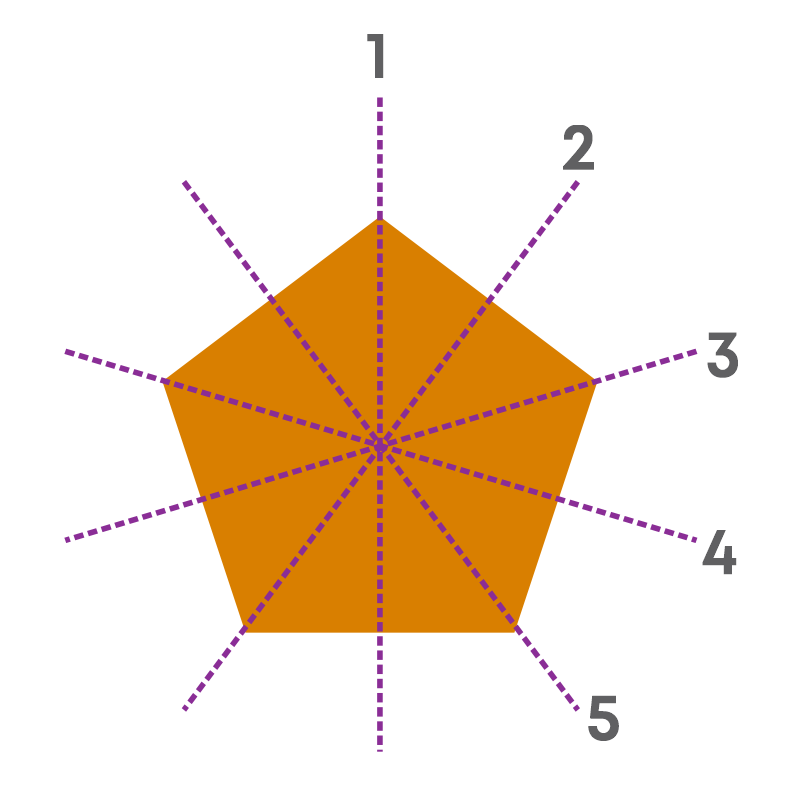
Now, we know that a square is a regular polygon and is symmetric. But, if we punch few holes into it as shown here, will it be still symmetric?

Let us now try to draw the lines of symmetry for the given regular polygon such that the punched holes are symmetric about the line.
We draw a vertical line, a horizontal line, and a slant line along a diagonal of the square and check whether we get the four holes about the lines symmetrically.

If we fold this figure at the slant and the vertical lines, we do not get the four holes symmetrically about the fold.
Hence, they are not lines of symmetry. If we fold this figure at the horizontal line, we get the four holes about the fold symmetrically.
Hence, it is a line of symmetry. Thus, we can draw only one line of symmetry for this figure.
Now, let us find the other hole so that the dotted line is the line of symmetry:

We measure the distance of the hole from the line of symmetry and then find the other hole.
Hence, in this way, we can find the other hole so that the dotted line is the line of symmetry.
Let us complete the polygon.
Step 1:
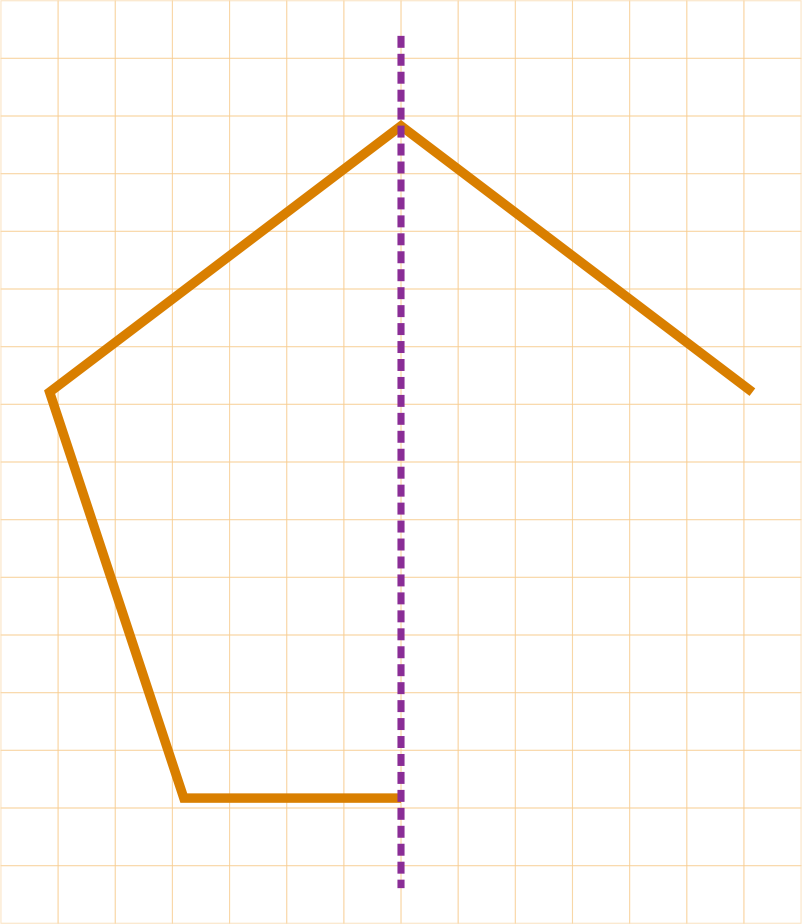
Step 2:
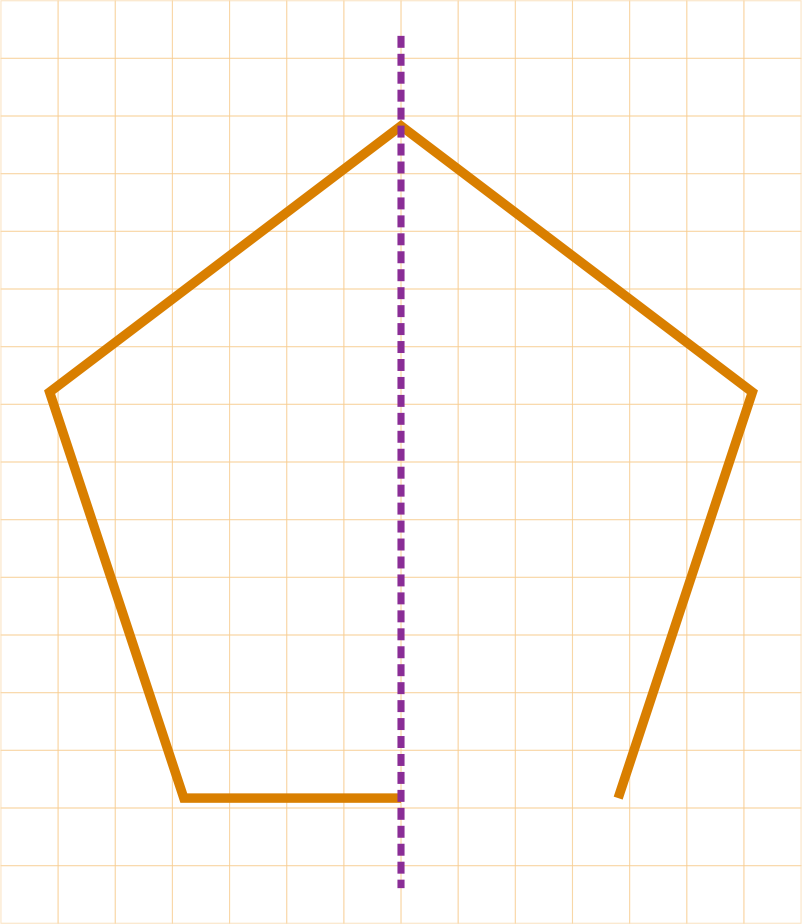
Step 3:
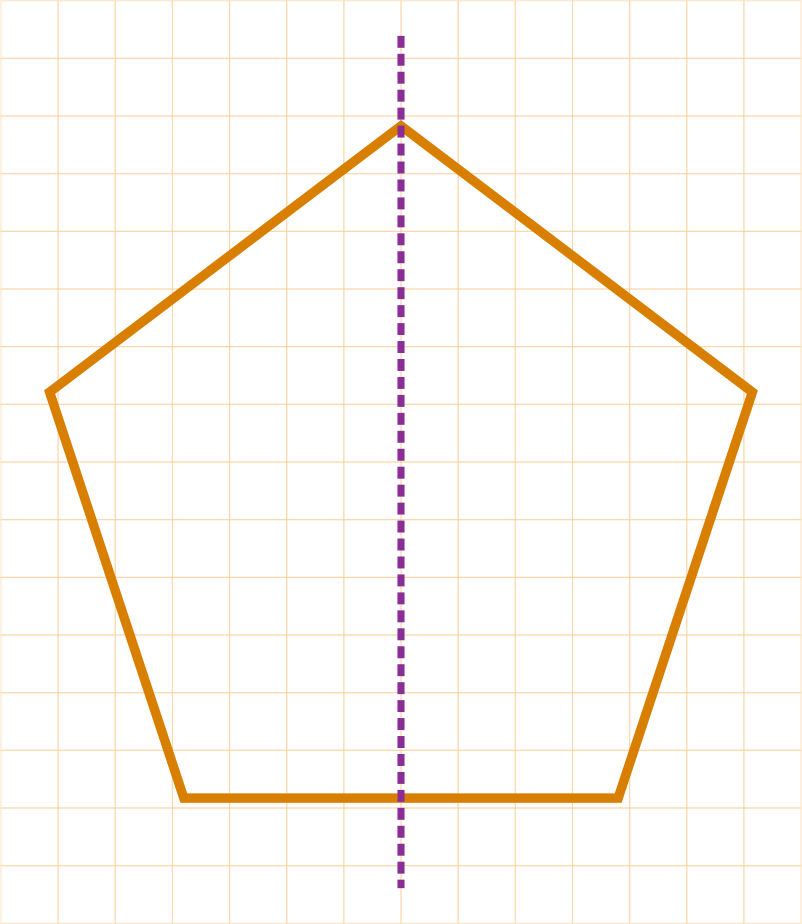
Rotational Symmetry
Look at the movement of the spinning bicycle wheel shown below.
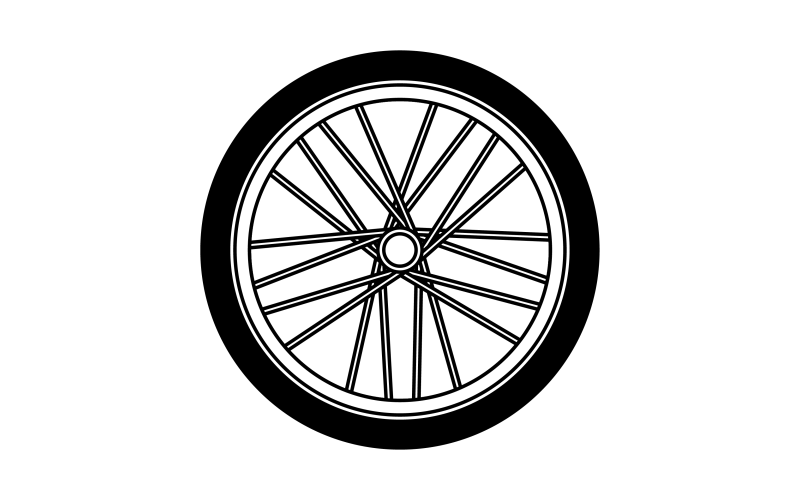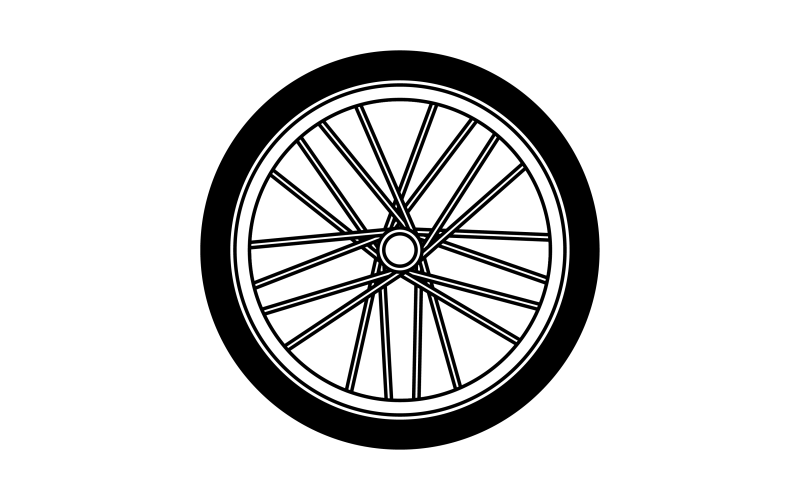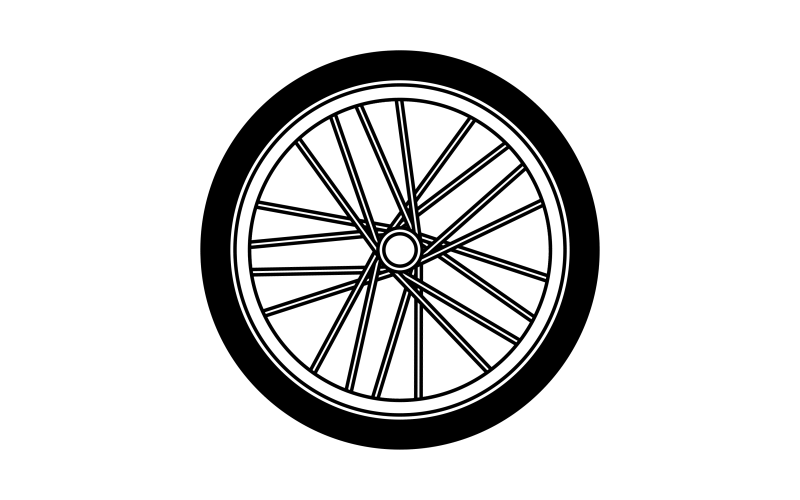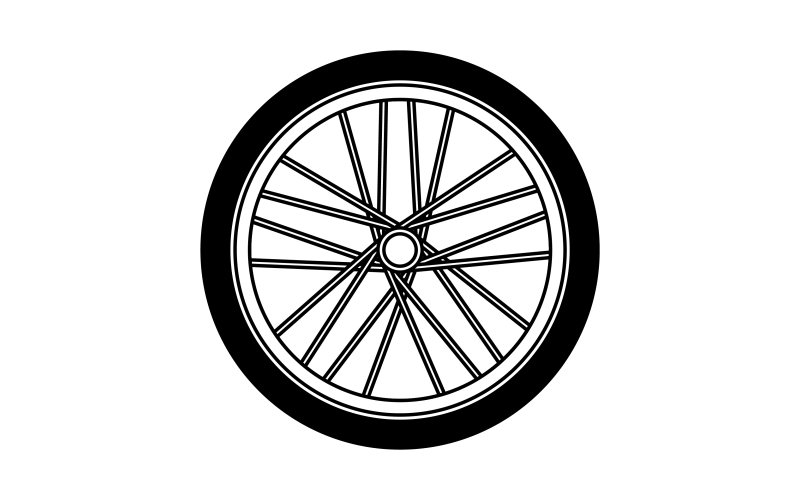
We say that the spikes of the wheel rotate.
The rotation of the hands of a clock is called the clockwise rotation whereas the opposite of clockwise rotation is called anticlockwise rotation.
Now look at the rotation of the wheel given below:

The spikes of the wheel rotate in an anticlockwise direction.
Some objects or shapes, when rotated about a particular point, will look exactly the same as the original figure. This is called rotational symmetry. Some objects or shapes can be rotated through a certain angle.
An object or shape has rotational symmetry if it looks exactly like the original object or shape after some rotation less than one turn or after one turn.
For the rotation of the design shown below, we say that it rotates about the fixed point marked by a star sign at the centre of the square.
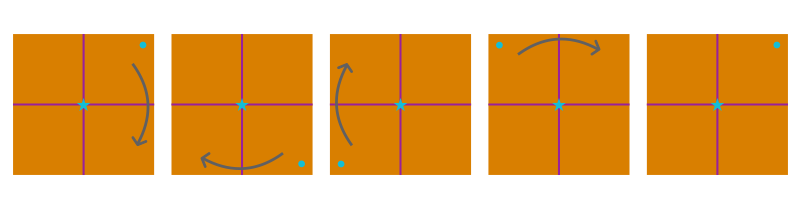
Also, rotation does not change the shape and size of the object.
- A full turn means rotation by 360⁰.
- A half turn means rotation by 180⁰.
- A quarter turn means rotation by 90⁰.
Let us consider the figure shown below:

Does this figure show rotational symmetry about a fixed point at the centre? If yes, then what is this fixed point called?
This fixed point is the centre of rotation.
- The angle through which the figure rotates is the angle of rotation.
- The number of times the figure looks exactly the same as the original figure in a full turn is the order of rotational symmetry.
The centre of rotation of an object is the fixed point around which the rotation occurs. For the rotating object shown below, the point at the centre is the centre of rotation.

Observe the given figure. When it is rotated clockwise through a quarter, what is the angle it covers?

It covers 90⁰.
When the figure is rotated clockwise through the next quarter, what is the angle through which it has rotated?

It is 180⁰.
When the figure is rotated clockwise again through the next quarter, what is the angle through which it has rotated?

It is 270⁰.
Rotating the figure again through the next quarter, what is the angle through which it has rotated now?

It is 360⁰.
Consider the object shown below:
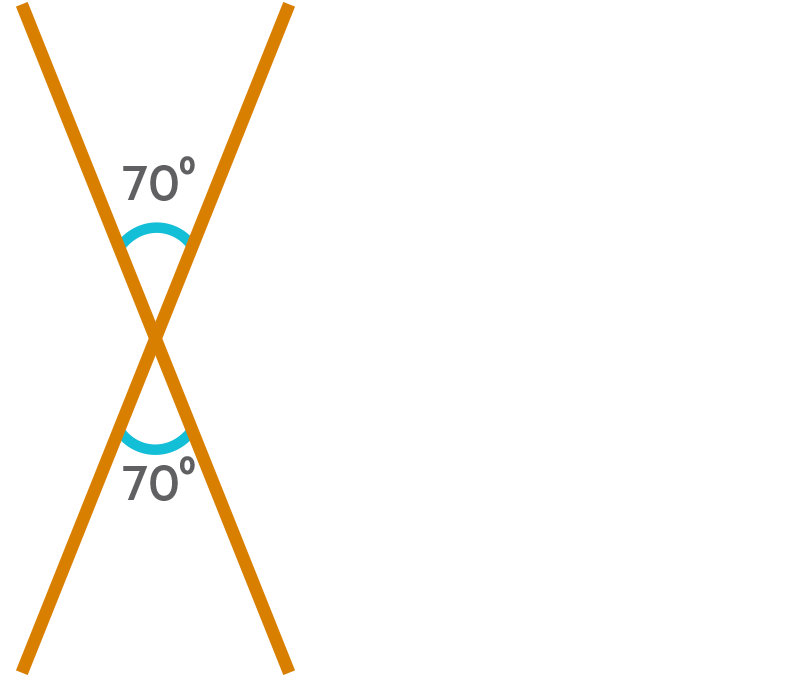
Let us rotate the object by 180⁰ clockwise.
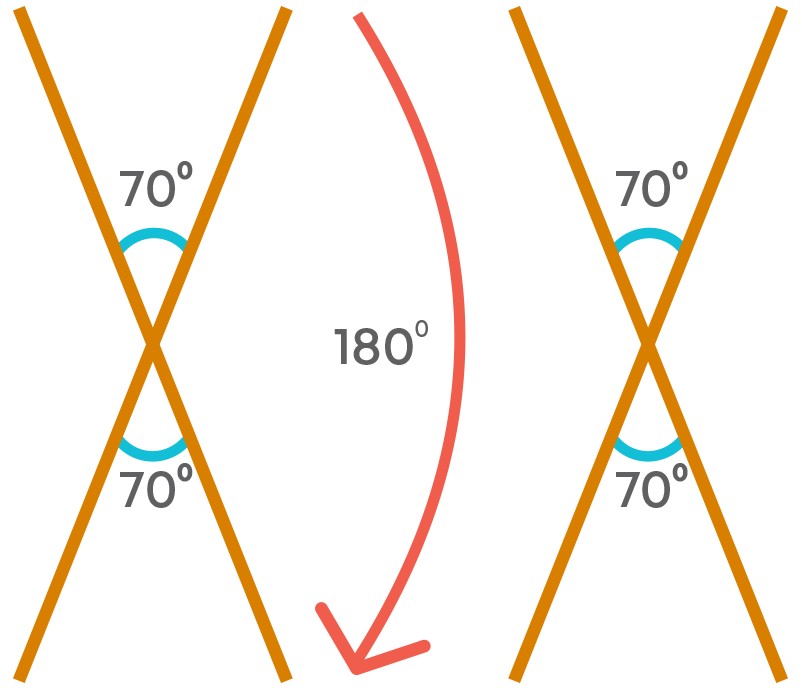
Now let us again rotate the object by 180⁰ clockwise.
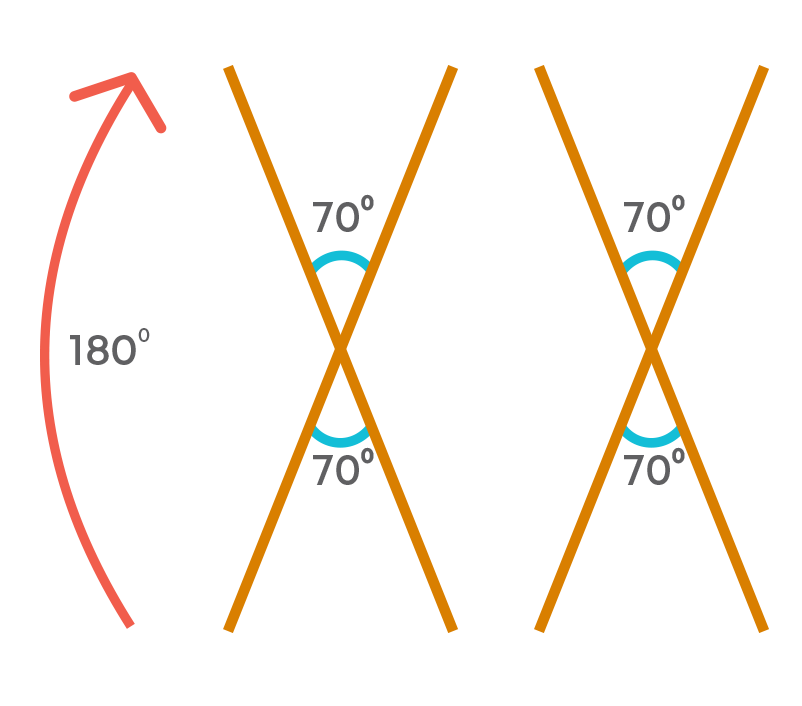
Hence, there are two times when the object looks exactly the same during the rotation.
So, the order of rotational symmetry is 2.
- If an object has ‘n’ positions when it looks exactly the same in a full turn, the object has rotational symmetry of order ‘n’.
- Every object has rotational symmetry of order 1 or more.
Consider the rotation of the circle shown below.

The centre of rotation is the centre of the circle. It looks the same during rotation through any angle. So, the circle has rotational symmetry.
Consider the isosceles triangle shown below:
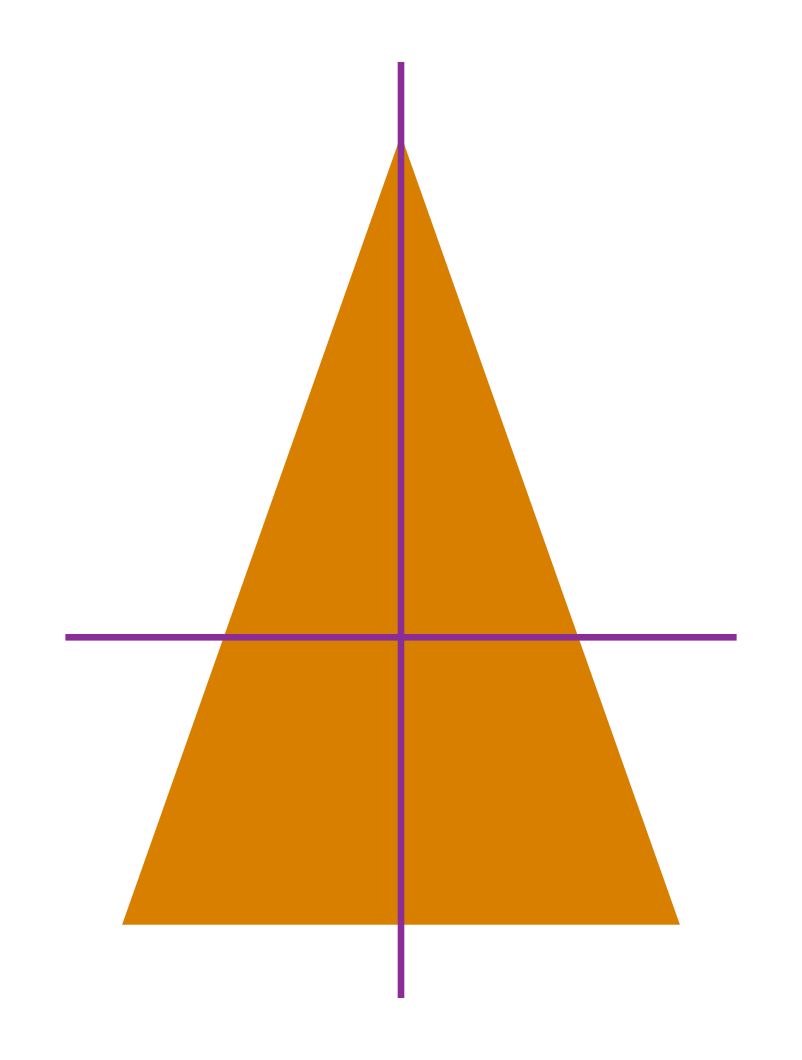
Let us rotate it by 90⁰ clockwise.

The triangle obtained is not exactly the same as the original, so let us rotate it again by 90⁰ clockwise.
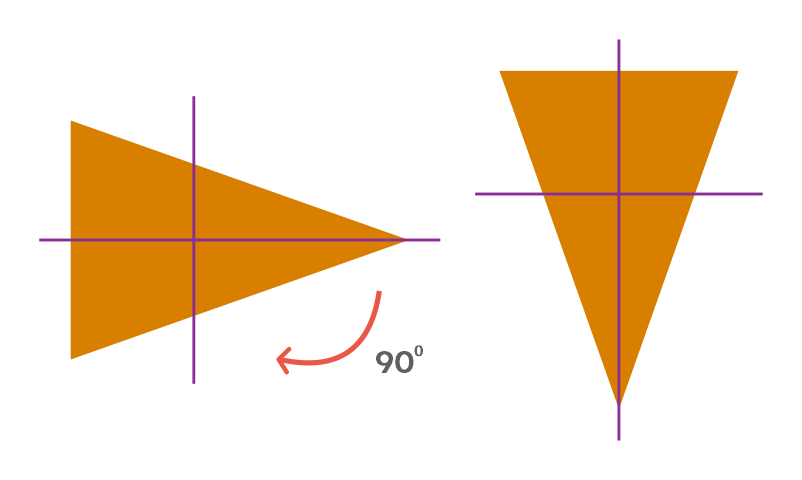
Still, the triangle obtained is not exactly the same as the original, so let us rotate it again by 90⁰ clockwise.
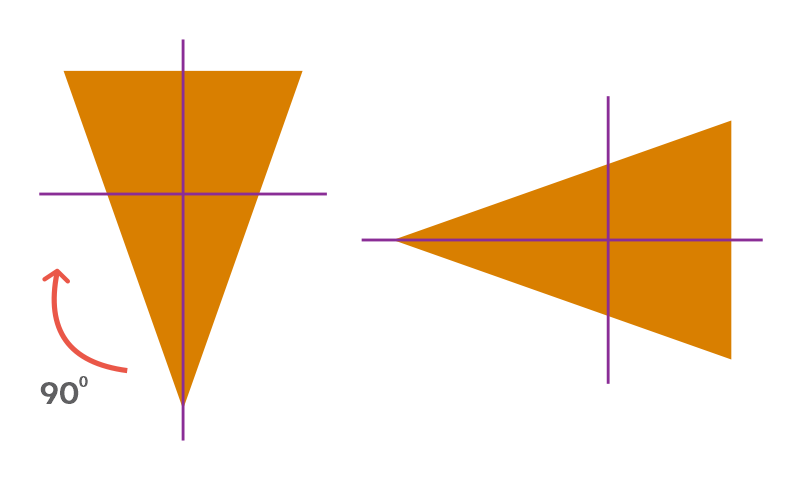
This time as well, the triangle obtained is not exactly the same as the original. So, let us rotate it again by 90⁰ clockwise.
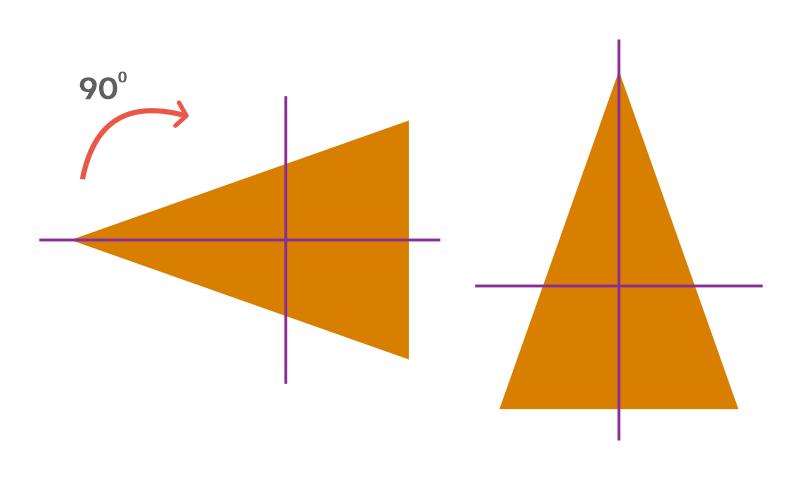
In a complete turn of 360⁰, the number of times an object looks exactly the same is one.
The isosceles triangle looks exactly like the original only once in a full rotation of 360⁰.
So, it has rotational symmetry of order 1.
Consider the rotation of the objects shown below:

For every object here, the centre of rotation is the centre of the objects.
Consider the letter given below.

The centre of rotation is marked by ‘+’ sign.
Now let us see how the letter looks after rotating it by 45⁰ clockwise.

If the letter is rotated by 90⁰ clockwise we get:

If the letter is rotated by 180⁰ clockwise we get:

Line Symmetry and Rotational Symmetry
The circle is a special case, having both line symmetry and rotational symmetry. Consider the rotation of the circle shown below:

The centre of rotation is the centre of the circle. It looks the same during rotation through any angle. So, a circle has rotational symmetry. Also, it has infinitely many lines of symmetry.
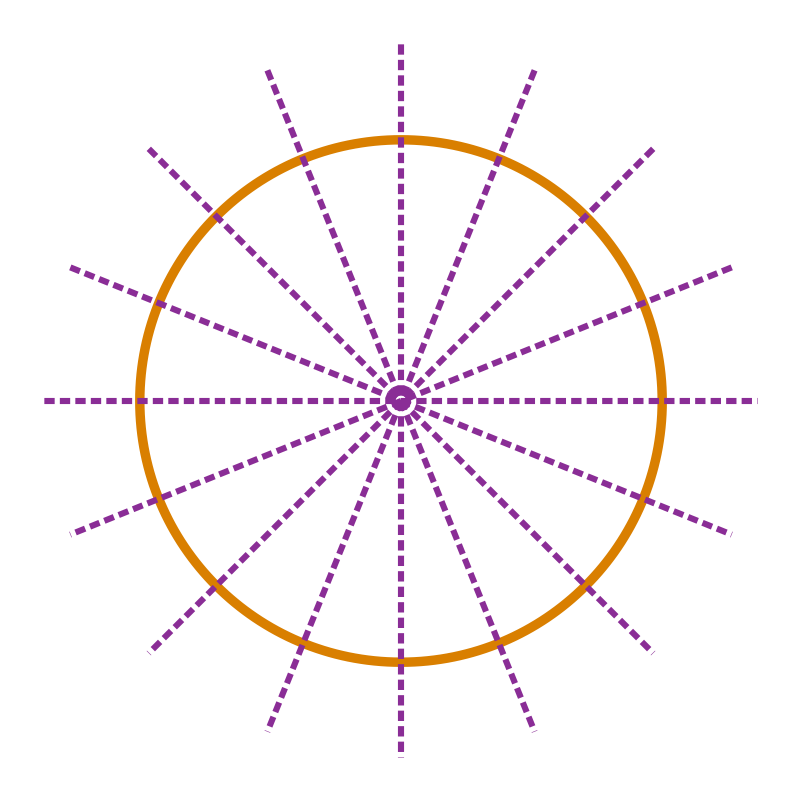
So, a circle has both line symmetry and rotational symmetry.
Consider the isosceles triangle shown below:
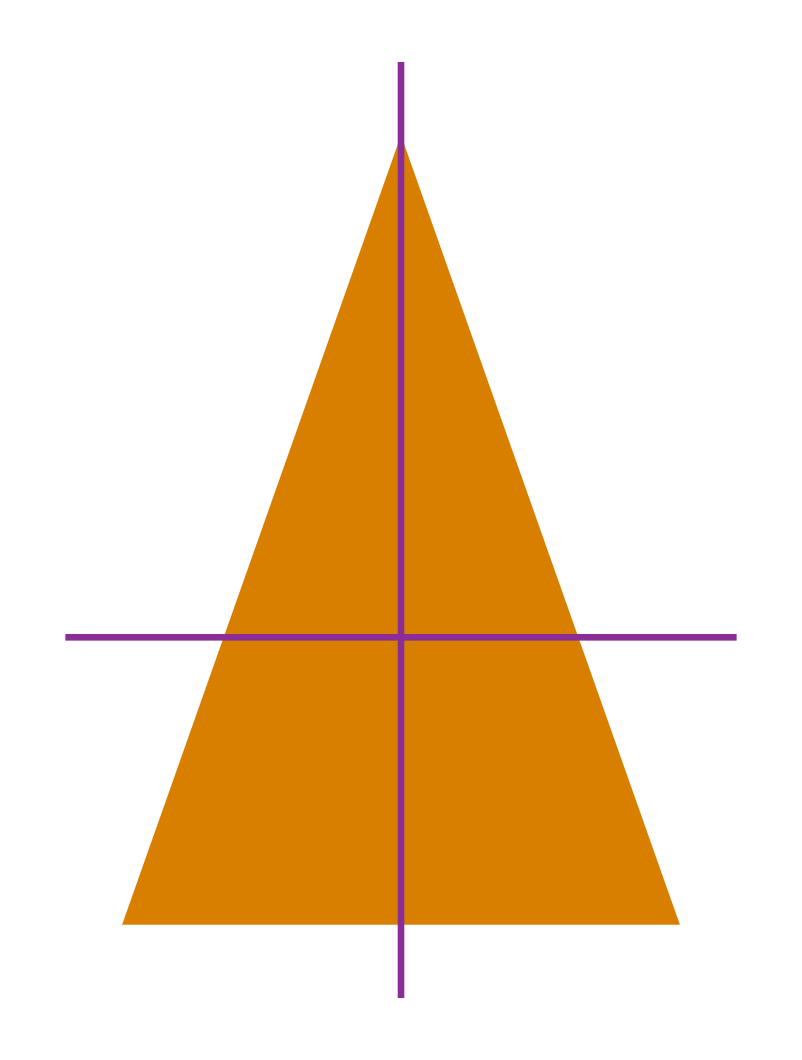
This triangle has a vertical line as the line of symmetry. So, it has line symmetry. In a complete turn of 360⁰, the number of times an object looks exactly the same is one.
So, it has rotational symmetry of order 1. Hence, some figures have line symmetry but no rotational symmetry of order more than 1.
Let us draw letters of the English alphabet having a line symmetry and rotational symmetry of order 2.
Consider the letter given below:

Clearly, this letter has two lines of symmetry. So, it has line symmetry.
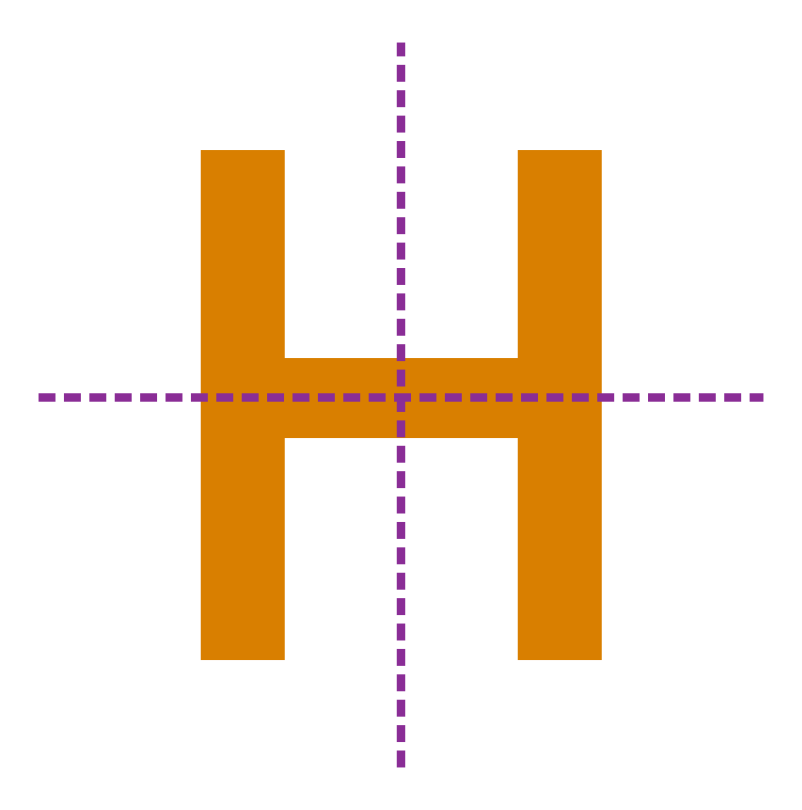
Also, it has rotational symmetry of order 2 as in a complete rotation of 360⁰, the number of times it takes the same position as the initial position is 2.
The dot in the figure is only for reference to trace the rotation. Do not consider it to be a part of the figure.

Consider the figure shown below:

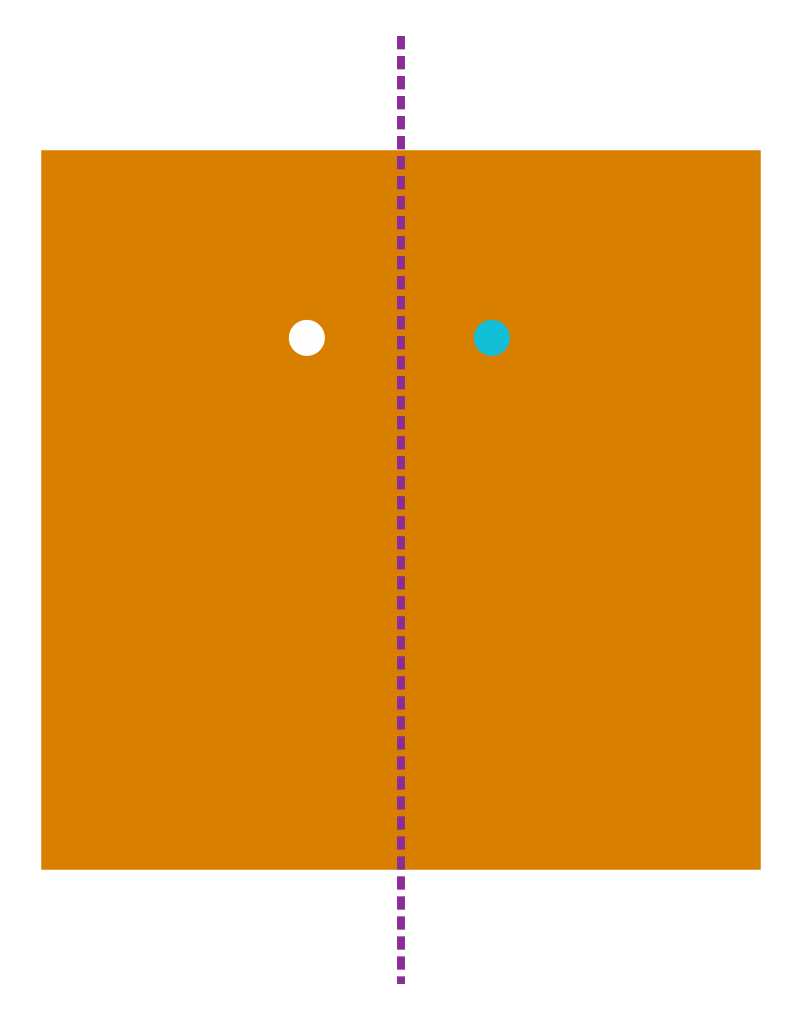
A parallelogram has no line of symmetry as no line divides it into two symmetrical halves.
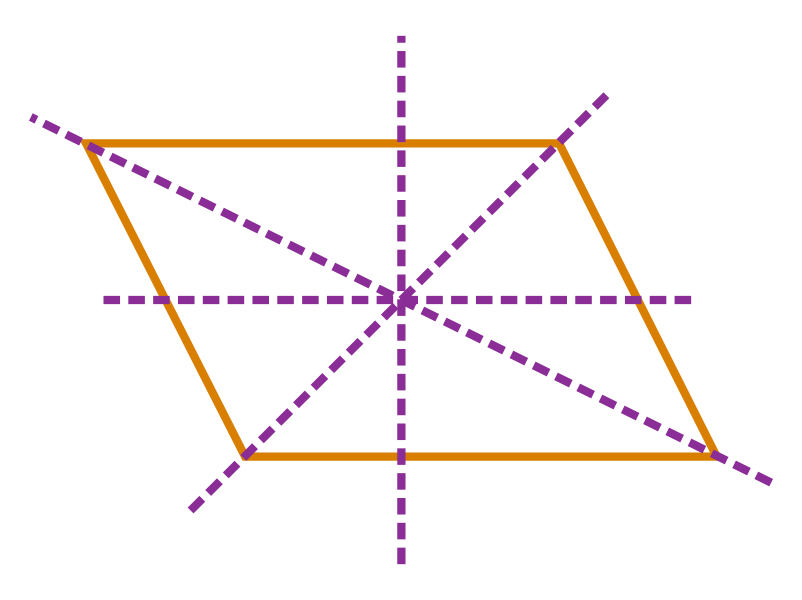
So, it has no line symmetry. In a complete turn of 360⁰, the number of times the parallelogram looks exactly the same is 2.

So, it has rotational symmetry. Hence, some figures have rotational symmetry but no line symmetry.
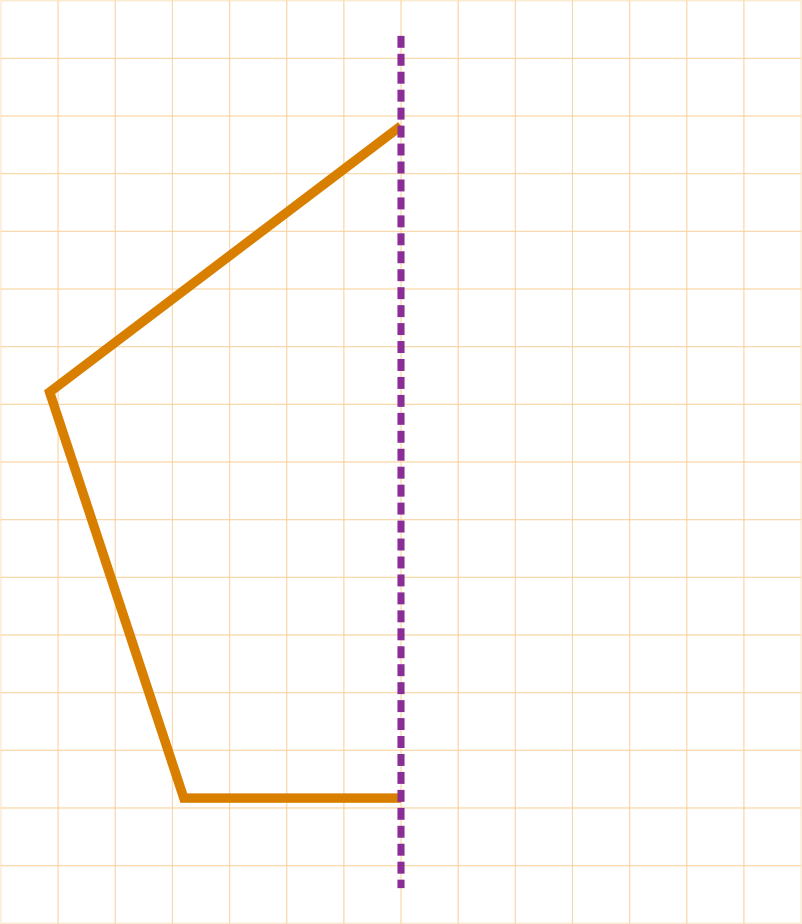
Let us draw a quadrilateral having line symmetry but no rotational symmetry of order more than 1.
Consider the quadrilateral given below:

Clearly, this quadrilateral has one line of symmetry, so it has line symmetry.
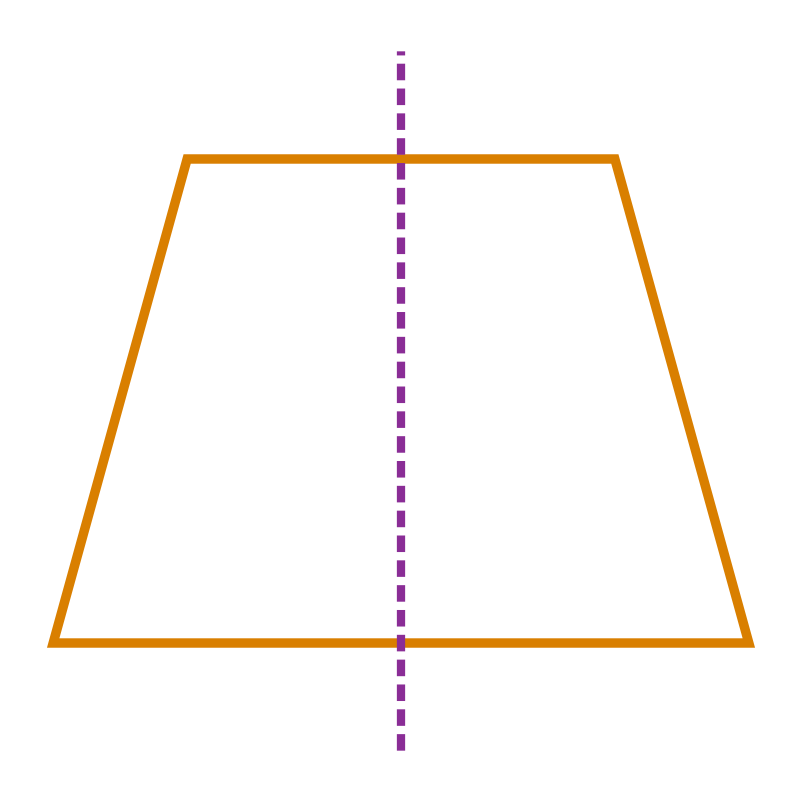
Also, it has no rotational symmetry of order more than 1 as in a complete rotation of 360⁰. So the number of times it takes the same position as the initial position is 1.

Common Errors
The following are topics in which students make common mistakes when dealing with symmetry:
- 1. A figure can be either symmetric or asymmetric
- 2. Line of symmetry is not always a horizontal line
- 3. Number of lines of symmetry for a regular polygon
- 4. Rotational symmetry is not the same as line symmetry
- 5. It is order of rotational symmetry for an object, not order of rotation
- 6. Every object has rotational symmetry
A Figure Can Be Either Symmetric Or Asymmetric
A figure can be either symmetric or asymmetric but cannot be both.
Figures having line/lines of symmetry are symmetric. Figures having no line/lines of symmetry are asymmetric.

Line Of Symmetry Is Not Always A Horizontal Line
The line of symmetry may be vertical or horizontal or slant. The given letter has both vertical and horizontal lines of symmetry.


Number Of Lines Of Symmetry For A Regular Polygon
We don’t need to draw lines of symmetry to find the number of lines of symmetry for regular polygons.
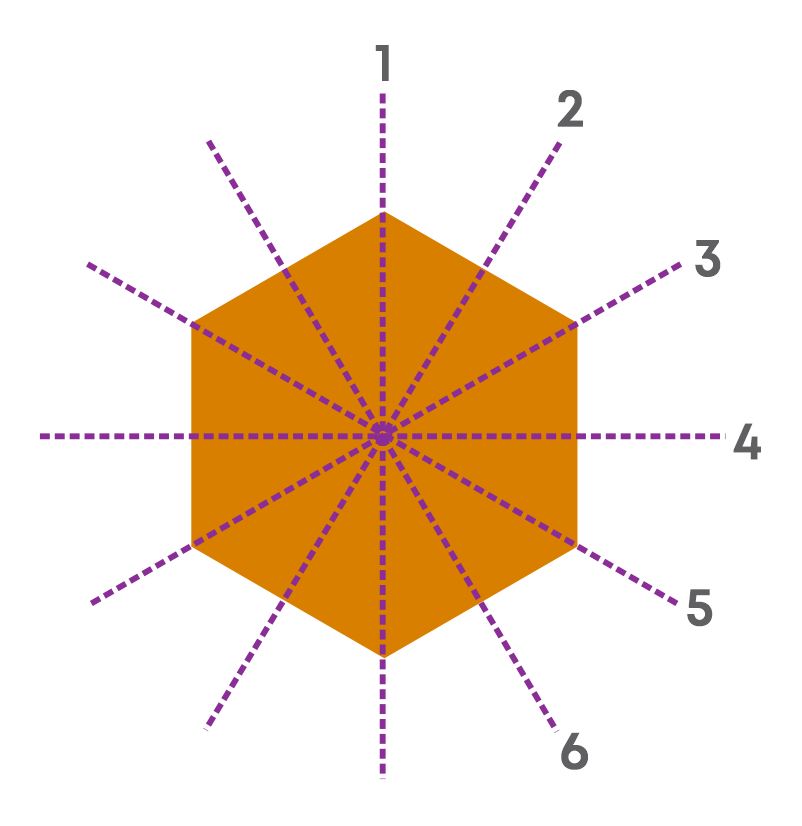
Remember! Each regular polygon has as many lines of symmetry as its sides.
The number of lines of symmetry for a regular hexagon is 6.
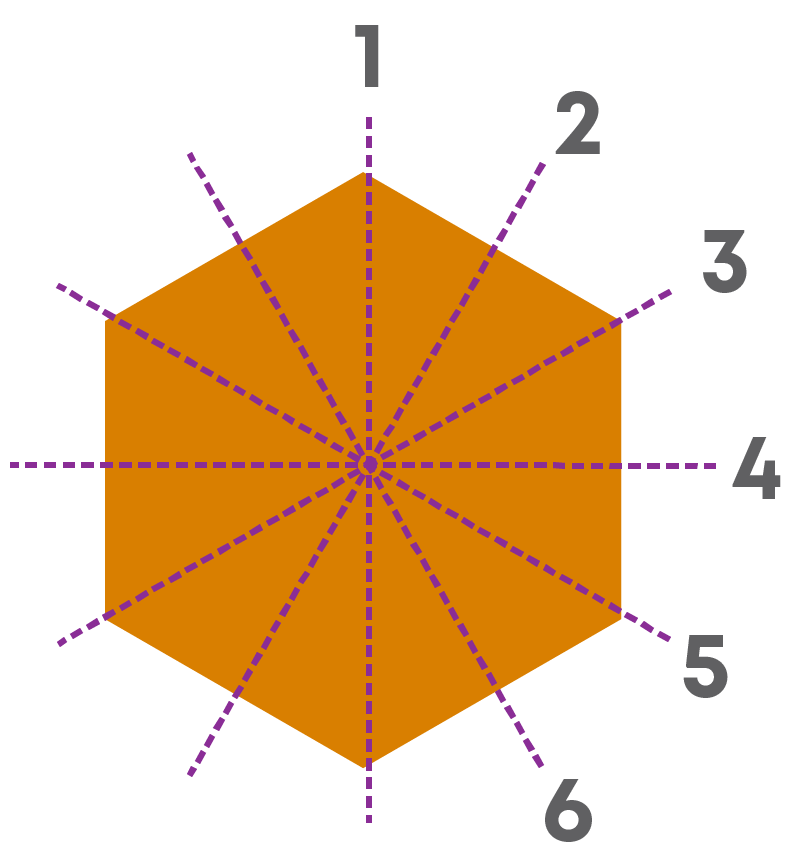
Rotational Symmetry Is Not The Same As Line Symmetry
An object or shape has rotational symmetry if it looks exactly the same as the original object or shape after some rotation less than one turn or after one turn.
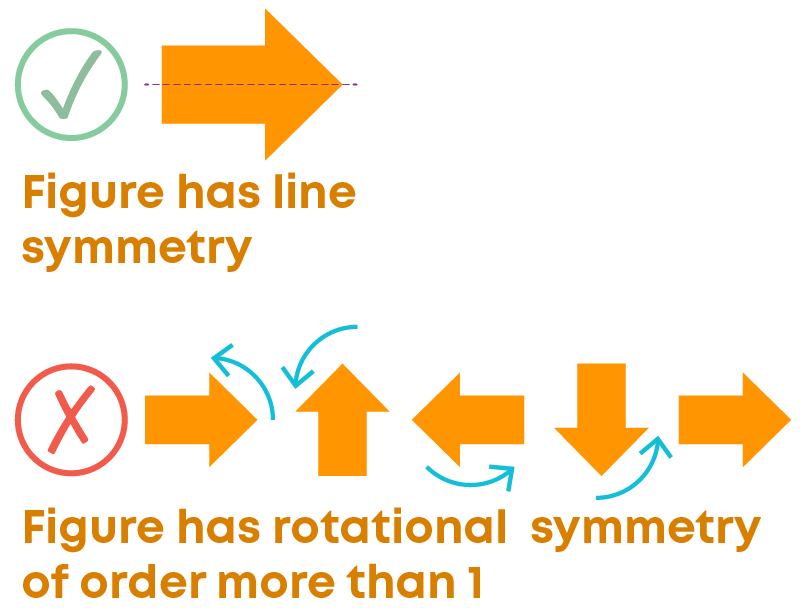
An object having a line/ lines of symmetry is said to have line symmetry. So, rotational symmetry is not the same as line symmetry.

The figure has one line of symmetry so it has line symmetry. Also, only after one turn, it looks the same as the original or takes the same position as the original one, so the order of rotational symmetry is 1. Hence, this figure has line symmetry but no rotational symmetry of order more than 1.
It Is Order Of Rotational Symmetry For An Object, Not Order Of Rotation
In a complete turn of 360⁰, the number of times an object looks exactly the same as the original object is called the order of rotational symmetry for the object, not the order of rotation of the object.
Every Object Has Rotational Symmetry
In a complete turn of 360⁰, the number of times an object looks exactly the same as the original object is called the order of rotational symmetry for the object.
As in a complete turn of 360⁰, every object looks exactly the same as the original at least once, i.e., after one complete turn; so every object has rotational symmetry of at least order 1.
So, every object has rotational symmetry.
Conclusion
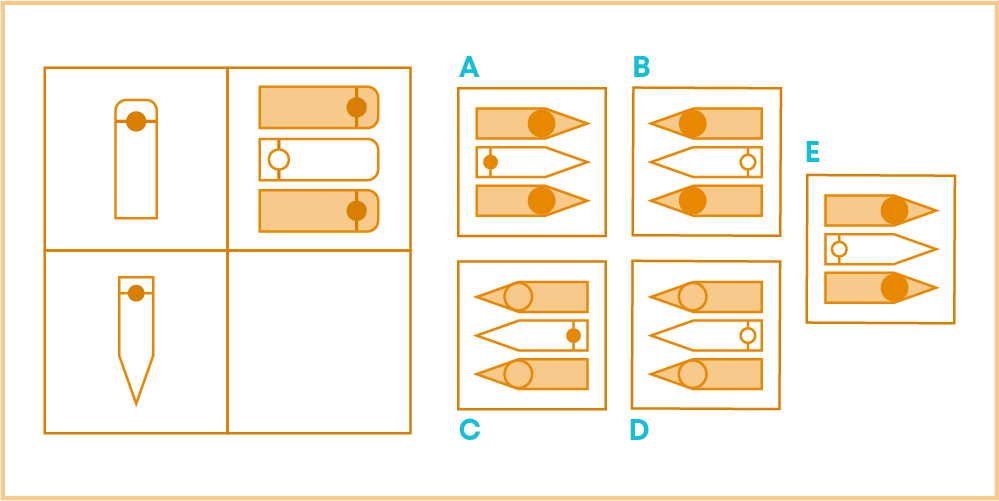
You have learnt all about symmetry in this blog. Can you solve this riddle?
Choose the option which will complete the pattern drawn on the left side: