Introduction
Perimeter is the total length or total distance covered along the boundary of a closed shape. It can also be defined as the length of the outline of a shape.
We know that perimeter of a closed figure is the distance around it and the area is the part of the plane or region occupied by the closed figure. Watch the video to explore more about perimeter and area.
If you live in an apartment, you will notice that the apartment has a main gate and outer walls which form the ‘fence’ of the building. Similarly, an independent house has fencing all around it to separate it from others. In both the cases, the length of the fence around the building is the perimeter of the outer area.

Concepts
The chapter ‘Perimeter and Area’ covers the following concepts:
Squares and Rectangles
TA square has all its sides equal in length and a rectangle has its opposite sides equal. A square is a special kind of a rectangle whose all sides are equal in length. Now, let us have a look at the two rectangles below: one is vertical, and the other is horizontal.
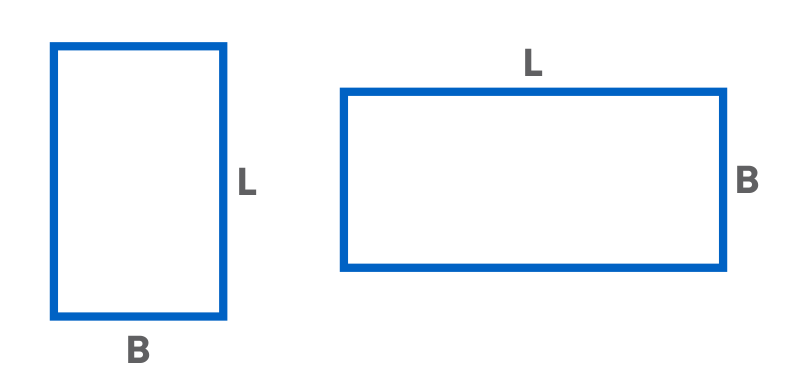
What can you see? We can see that in the first figure, the length is the longest side and in the second figure breadth is the longest side. Is there any special rule to decide as to which side will be the length and breadth? No! there is no such rule.
Also, instead of saying length and breadth, we can say side 1 and side 2 or adjacent sides.

So, the perimeter of a rectangle = 2 (Side 1 + Side 2)
Or in other words,
the perimeter of a rectangle = 2 × the sum of adjacent sides
Area of a rectangle = Side 1 x Side 2
Or in other words,
Area of a rectangle = the product of adjacent sides
The amount of surface enclosed by a closed figure is called its area. Now let us consider the two rectangles below:
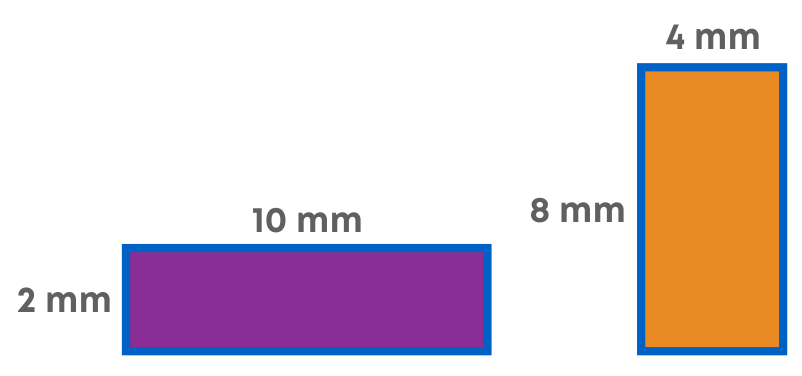
What is the perimeter of the two rectangles? The orange rectangle has a perimeter of 24 mm and the purple rectangle also has a perimeter of 24 mm. What about their areas? Do they have the same area?
Area of the orange rectangle = 33 mm
Area of the purple rectangle = 20 mm2
They do not have the same area. So, rectangles with the same perimeter can have different areas. Rectangles having the same area can have different perimeters.
Observe the shapes 1, 2, 3 and 4 in the figure.
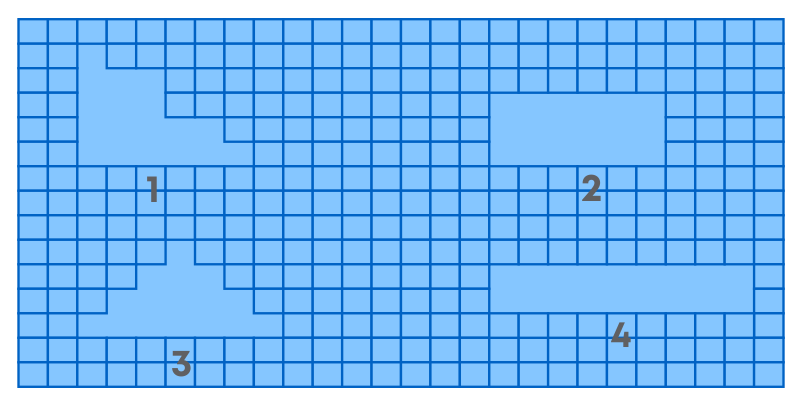
How do we find the perimeter of any figure? Perimeter is the length of the boundary of any shape. Here each shape is made of squares of 1 unit. Hence, if the sides of a shape are made of 12 sides of squares, then its perimeter will be 12 units. How about the area?
We know that area is the total space occupied inside a shape. Hence, we must count the number of squares inside the shape. So, if a shape has 12 squares in total, then its area is 12 sq. units.
Area of a square = side × side

Area of a rectangle = length × breadth
Perimeter of a rectangle = 2 × (length + breadth)
Perimeter of a square = 4 × length of one side
Remember, to find the area between two rectangles:
Area of the remaining part of the rectangle = Area of the big rectangle – Area of the small rectangle
When the area and a side of a rectangle are given, find the missing side by using the formula of the area of a rectangle and then find the perimeter.
When the perimeter and a side are given, find the missing side by using the formula of the perimeter of a rectangle and then find the area.
Consider this example: Manoj walks around a rectangular park with area 920 m2 and length 40 m. Manoj wants to know how long he walks once around the park. Let us help Manoj to find the distance he walks once around the park.
To find the distance around the park we must first find the breadth of the park.
We know that area of a rectangle = length × breadth
920 m2 = 40 m × breadth
Breadth = 920 40
= 23 m
We know that the perimeter of the rectangular park is the total distance around the park. To find the distance covered by Manoj in one round, we need to find the perimeter of the park.
Perimeter = 2 × (40 m + 23 m)
= 2 × 63 m
= 126 m
Hence, Manoj covers 126 m by walking once around the park.
Rectangles
A rectangle can be divided into congruent parts. Figures having the same shape and size are known as congruent figures.
To check whether the parts are congruent or not, superimpose one part onto the other, if they match, they are said to be congruent. Congruent parts have the same size and area.

If we superimpose one figure over the other and they fit onto each other, then they are said to be congruent shapes. They will have the same shape and size.
Consider the triangles ABC and PQR.

Both have the same size and shape and hence, they are congruent. So, this can be expressed as
∆ABC ≅ ∆PQR
Take a rectangle and cut the rectangle along its diagonal to get two triangles. Superimpose one triangle onto the other.
Note: To superimpose, we will have to rotate the other triangle.
Are they exactly the same in size?


We can see that after superimposing, both triangles fit perfectly which implies that they are congruent to each other. Therefore, these two triangles have the same shape and size.
A rectangle of length 5 cm and breadth 4 cm is divided into two parts as shown below. Trace the rectangle on a sheet of paper and cut the rectangle along the line shown below to divide it into two parts.
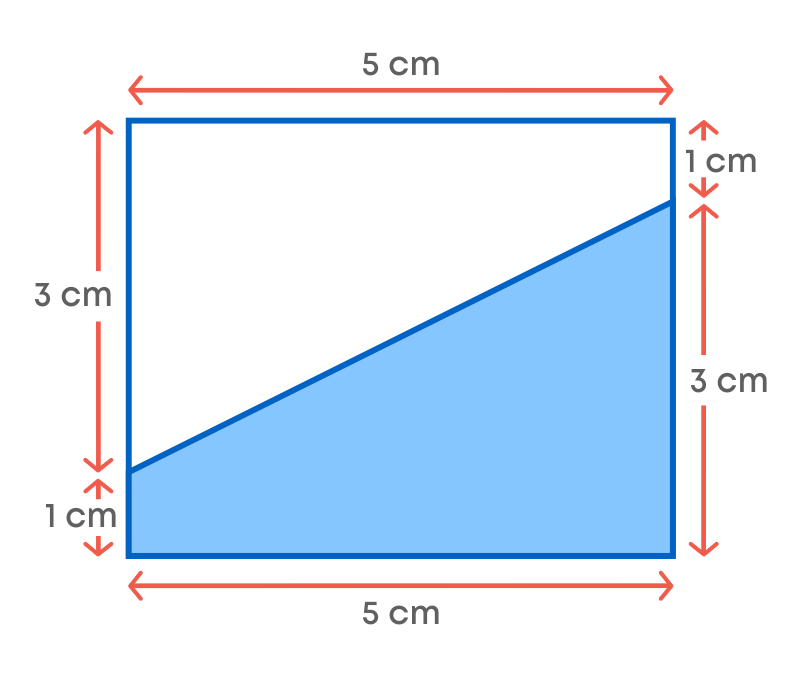
Superimpose one part on the other, see if they match. (You may have to rotate one of them)
Are they congruent? Yes! The two parts are congruent to each other.
Now, take a rectangle and cut the rectangle along its diagonal to get two triangles. Superimpose one triangle on the other. Are they exactly the same in size?


We can see that after superimposing both the triangles fit perfectly which implies that they are congruent to each other. Therefore, these two triangles have the same shape and size. Since two parts of the triangles are congruent, they have the same area.
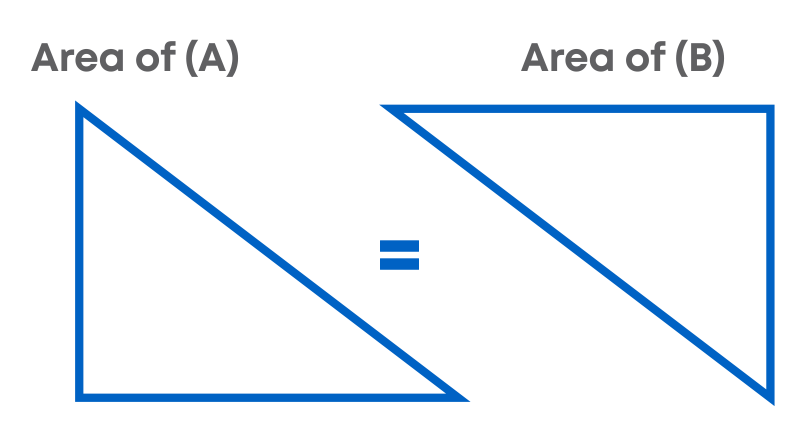
Together these two triangles form a rectangle.
We can also write this as,
Area of triangle(A) + Area of triangle(B)
= Area of rectangle
The triangular parts have the same area so,
Area of rectangle
= 2 × area of triangle (A)
We can also write it as,
Area of each triangle
= 1 2 × area of triangle
We can also cut the same rectangle in some other shapes which are congruent to each other.

A rectangle of length 6 cm and breadth 4 cm is divided into two parts. Trace the rectangle on another paper and cut off the rectangle along EF to divide it into two parts. Superimpose one part onto the other, see if they match. (You may have to rotate them)

Are they congruent? Yes!
The two parts are congruent to each other. So, the area of one part is equal to the area of the other part.
Therefore, the area of each congruent part
= 1 2 × the area of the triangle
= 1 2 × (6 × 4) cm2
= 12 cm2
Parallelograms
To calculate the area of the parallelogram we use the formula:
Area of a parallelogram = base × height

The area of the given parallelogram
= DC × AE
The parallelogram shown below has an area of 80 units2.
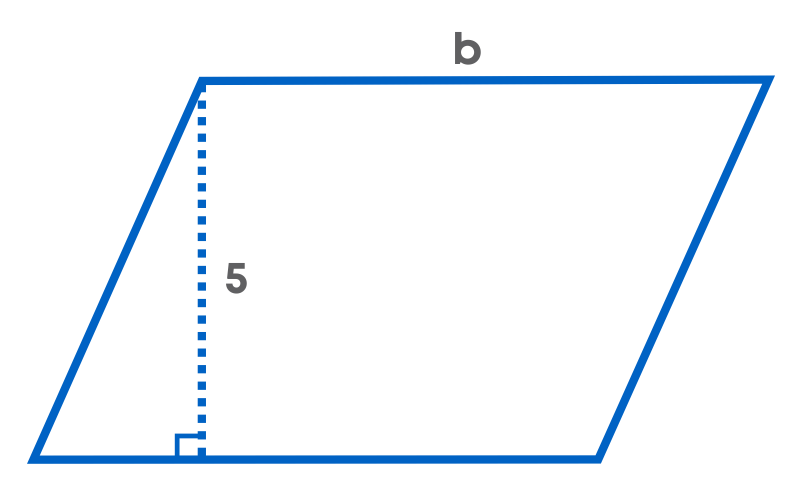
Find the missing base. How do we find the missing base? We know that the perimeter of a parallelogram = base × height
80 = base × height
80 = b × height
Hence, base (b) = 80 5 = 16 units.
Base of a parallelogram = area of the parallelogram height of the parallelogram
Height of a parallelogram = area of the parallelogram height of the parallelogram
Finding the missing dimensions in parallelograms requires us to work backwards.
We can figure out a missing dimension if we have been given the area and another measurement, such as the area and the height or the area and the base.
The area of a parallelogram is determined by multiplying the base and the height.
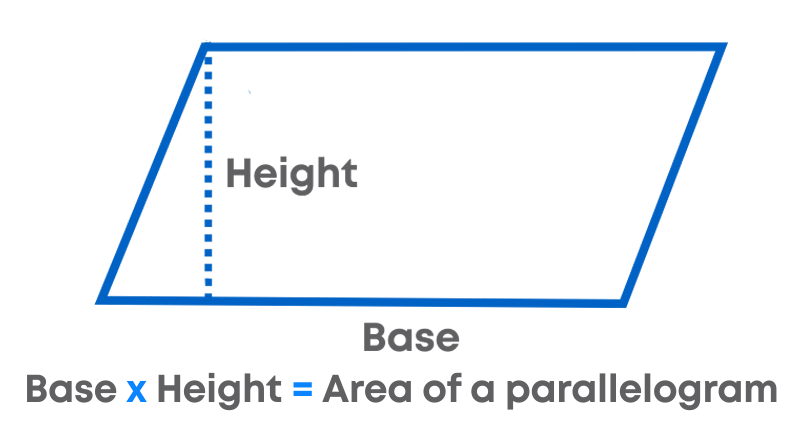
If you know the area and the base or the area and height, you can use this formula to find the missing dimension.
Triangle
Observe the given triangles. What do you notice?
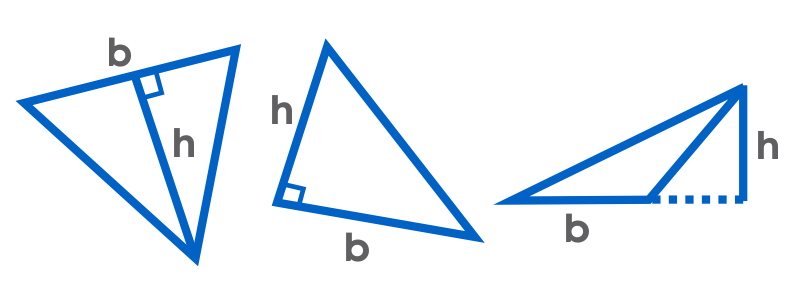
Any side of a triangle can be the base. The diagrams above show the length of the base (b) and the height (h) of the triangles.

We can see that both ∆ ABC and ∆ DEF are congruent to each other.
Now, place both the triangles in such a way that their corresponding sides AB and ED are joined as shown below.

The new figure thus formed is a parallelogram. Compare the area of each of the triangles to the area of the parallelogram. The base and the height of the triangles are the same as the base and the height of the parallelogram, respectively.
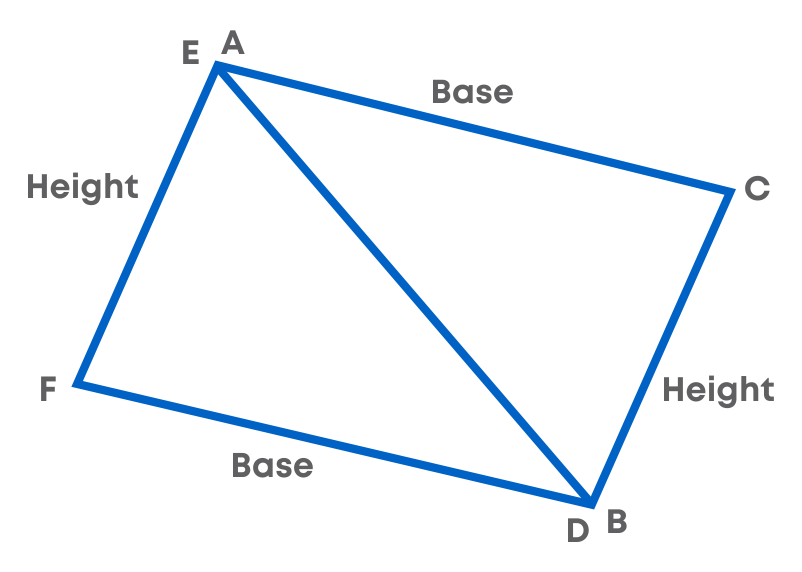
The parallelogram is made of two equal triangles.
We have,
Area of parallelogram = base x height
Therefore,
Area of each triangle
= 1 2 × (Area of the parallelogram)
= 1 2 × (base x height)
= 1 2 × (b x h)
Observe the figure given below:
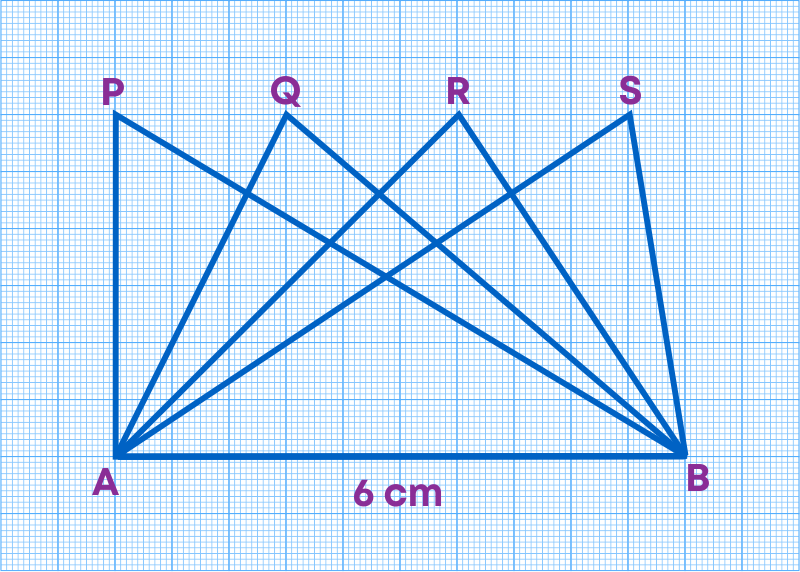
The triangles are on the base AB = 6 cm. What can you say about the height of each of the triangles corresponding to the base AB?
From the given figure, we can see that all triangles have the same base and the same altitude. Hence, they are equal in area.
All congruent triangles are equal in area but the triangles equal in area need not be congruent.
A gardener wants to know the cost of covering the whole of a triangular garden with grass.

We know that area is the total surface enclosed by a closed figure. In this case, we need to know the area of the triangular region.
Find the area of right - angled triangle ABC right angled at B, with one leg of length 20 cm and hypotenuse as 29 cm. Let us find the area of right - angled triangle ABC.
We are given,
- Height/Perpendicular (AB) = 20 cm
- Hypotenuse (AC) = 29 cm
- Base (BC) = ?
Let us use Pythagoras theorem to find the base (BC),
According to Pythagoras theorem, hypotenuse2 = perpendicular2 + base2
Base2 = hypotenuse2 - perpendicular2
(BC)2 = (AC)2 – (AB)2
(BC)2 = 292 – 202
(BC)2 = 841 – 400
(BC)2 = 441
BC = √441 = 21
So, the base BC is 21 cm.
We know that,
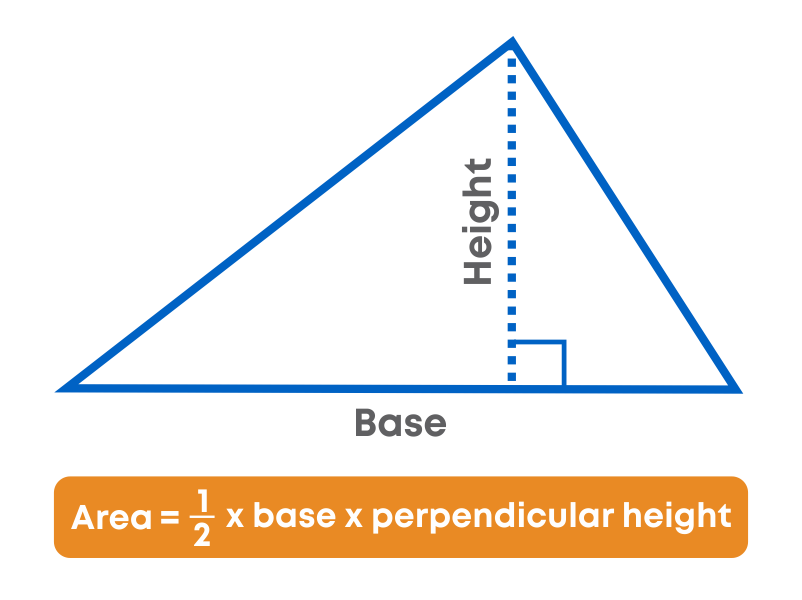
Area of a triangle = 1 2 × (base x height)
Area of right - angled triangle ABC = 1 2 × (BC × AB)
= 1 2 × (20 × 21)
= 210 cm2
Hence, the area of the right - angled triangle ABC is 210 cm2.
A triangular base of a prism has height 10 cm and base 15 cm; what will be the area of the triangular base? We know that,
Area of a triangle = 1 2 × (base x height)
Area of a triangular base = 1 2 × (20 × 15)
= 1 2300
= 150 cm2
Hence, the area of a triangular base of a prism is 150 cm2.
Remember, altitude of a triangle is the perpendicular drawn from a vertex of the triangle to its opposite side (this side is the base of the triangle). Also, the altitude, which is known as the height of the triangle, makes a right angle with the base. The picture below shows an altitude of a triangle.
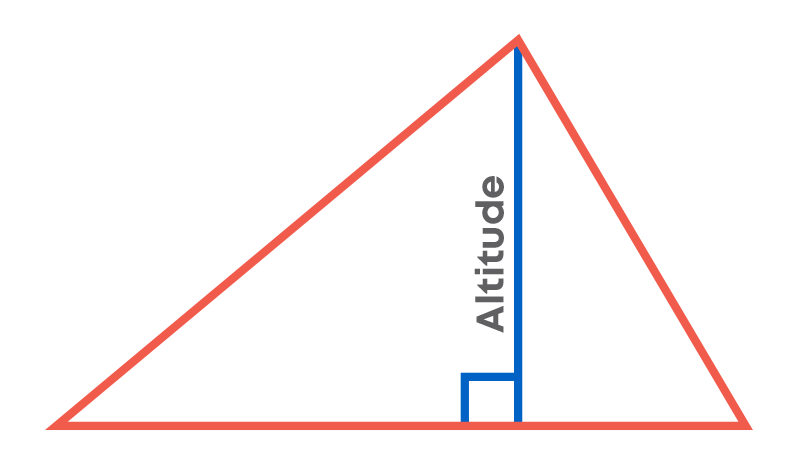
When a triangle is a right triangle, the altitude or the height is one of the legs if the other leg is the base. If the triangle is obtuse, then an altitude may be outside the triangle. If the triangle is acute, then every altitude will be inside the triangle. The red lines below are all altitudes.

There are 2 types of problems in finding the missing dimensions of a triangle.
Type 1: To find the altitude of a triangle when the area and base of the triangle are given, use the following formula:
Altitude of a triangle = Area × 2 Base
Type 2: To find the base of a triangle when the area and altitude of the triangle are given, use the following formula:
Base of a triangle = Area × 2 Base
Circles
The distance from one point on a circle through the centre to another point on the circle is called the diameter. It is also the longest distance across the circle and is twice the radius.
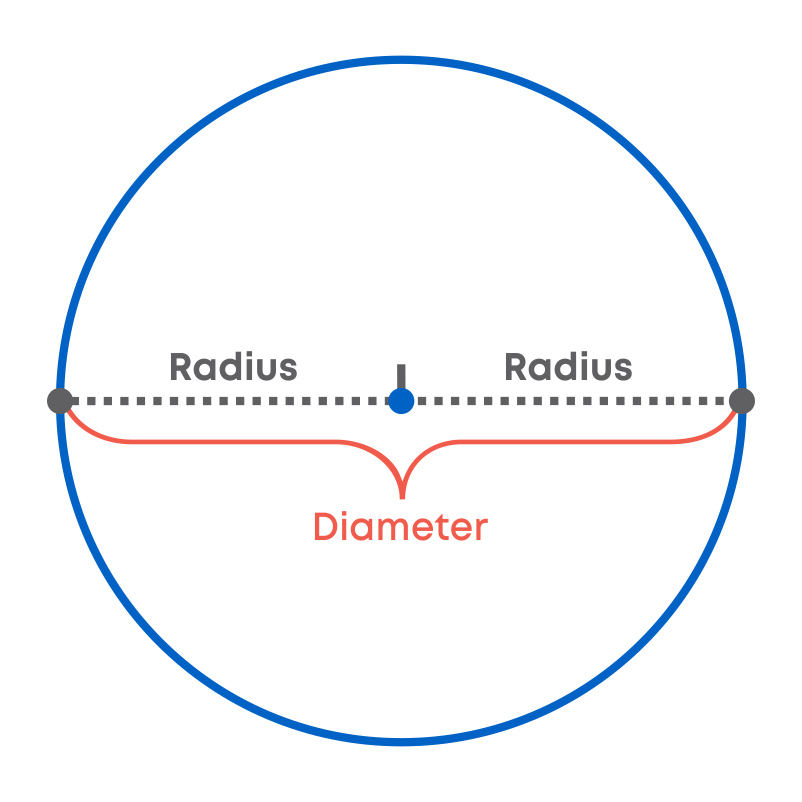
We know that a circle is a closed figure. The length of the boundary or the perimeter of a circle is called the circumference. To calculate the circumference of the circle we need to know the value of a special number π (pi). The ratio of the circumference of any circle to its diameter is always a constant value, 22 7, which is the value of pi.
For convenience in calculation, we round off the value of ‘pi’ to 3.14.
Circumference of the circle is the length of the boundary of the circle. If we cut open the circle and straighten it, the length of the boundary will be the measure of the circumference of the circle.
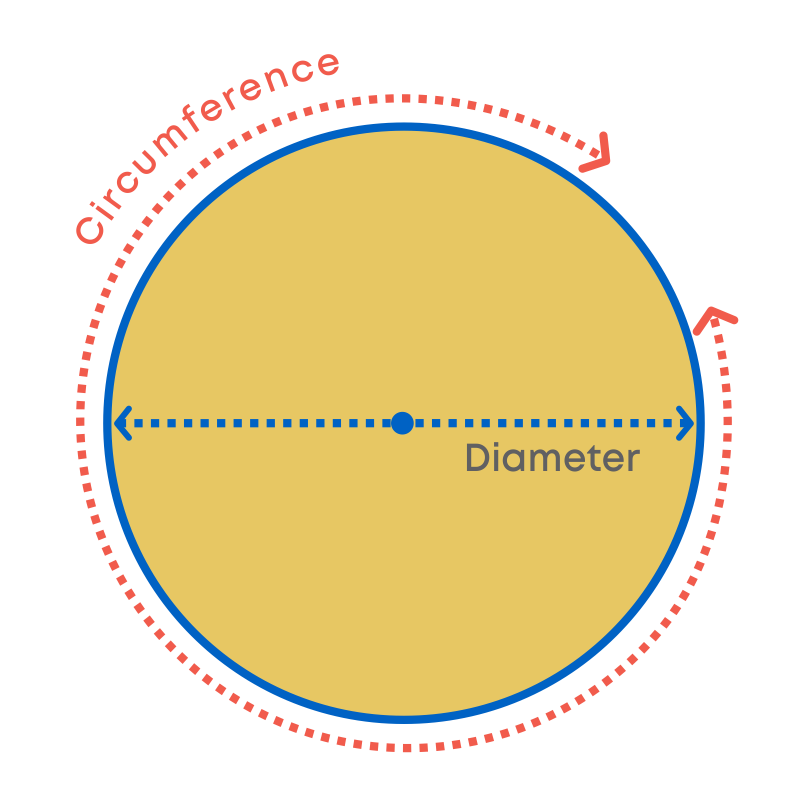
Consider the following table. We are given the radius, diameter, circumference and the ratio of circumference to diameter for 4 different circles.

We know that π = 22 7 = 3.14
So, we can say that c d = π, where ‘C’ represents the circumference of the circle and ‘d’
represents its diameter. Or we can write it as C = π × d.
We know that diameter (d) of a circle is twice the radius (r), i.e., d = 2 × r.
So, C = π × d
C = π × 2r or C = 2πr
We can conclude that:
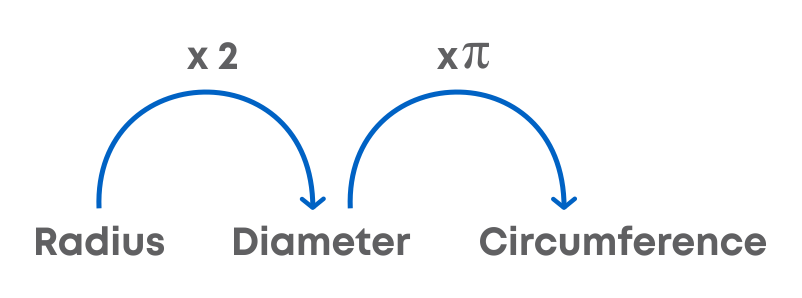
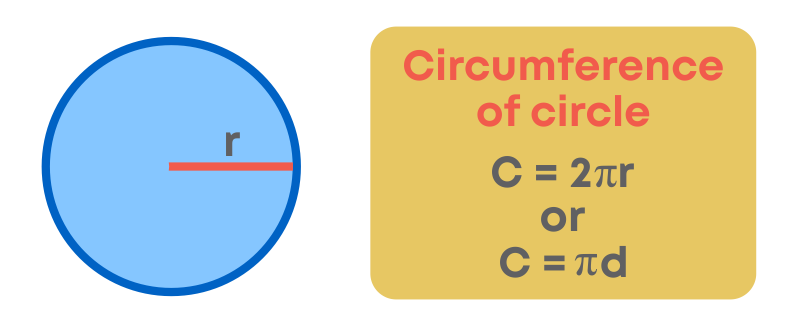
The perimeter of any shape is the total length of all its sides. Since a circle has no sides, its perimeter (also known as its circumference) is the length of the boundary of the circle.
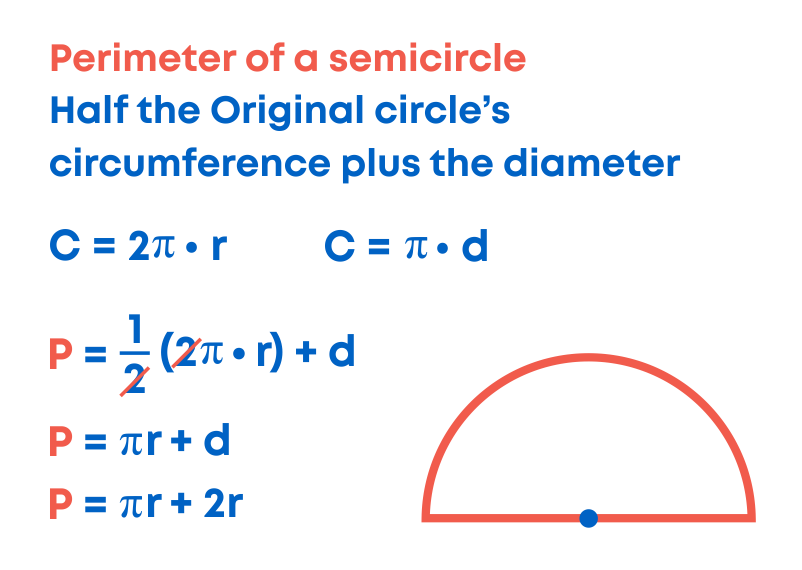
A semicircle is half a circle, so we'll need to divide the formula for the circumference of a circle by two.
The circumference of a circle is 2πr or πd. So, the circumference of a semicircle is 1 2 × πd or πr, where ‘r’ is the radius.

But if we divide the circumference of the circle by two, we get the measure of only the curved part of the boundary of the semicircle. The measure of the straight part of the boundary is not included in that.

Since a semicircle, unlike a circle, has a straight side, we need to consider that if we are going to find its total perimeter.
That side is its diameter. So, we just need to add the diameter to the formula we have already determined. So, perimeter of the semicircle is given by πr + 2r or πr + d.
We know how to calculate the circumference of a circle if radius or diameter is given. But how to calculate the radius/diameter when the circumference is given? We know that circumference of a circle is:
C = 2πr when the radius is given, and C = πd when the diameter is given.
Hence, we can write r = C 2π or d = C π
Where C = circumference, r = radius, d = diameter
A farmer digs a flower bed of radius 2 m at the centre of a field. He needs to purchase fertiliser. If 1 kg of fertiliser is required for 1 square metre area, how much fertiliser should he purchase?

What will be the cost of polishing a circular table-top of radius 3 m at the rate of ₹10 per square metre?
In such cases, we need to find the area of the circular region.
Let us find the area of a circle, using a graph paper. Draw a circle of radius 4 cm on a graph paper. Find the area by counting the number of squares enclosed.

As the edges are not straight, we get a rough estimate of the area of the circle by this method. The amount of space inside the circle is called the area of the circle.
We calculate the area of the circle using the formula:
Area of circle = πr2
where ‘r’ is the radius of the circle and π = 22 7
This formula is useful for measuring the space occupied by a circular field or a plot. Suppose you have to buy a table cloth, then with the formula you can calculate how much cloth is required to be bought.
Let us consider a problem.
If the circumference of a circular sheet is 154 m, find its radius. Also, find the area of the sheet.
How to calculate the radius or diameter?
We use the following formula to calculate the circumference of a circle:
C = 2πr when the radius is given, and C = πd when the diameter is given.
Hence, we can write r = C 2π or d = C π
Where C = circumference, r = radius, d = diameter
When we know the radius of the circle, we can use the formula A = πr2 to calculate the area of the circle.
What is a ring and how does it look?

A ring is a circular disk with a circular hole in it. The outer and inner circles that define the ring are concentric which means that they share a common centre.
The dimensions R1 and R2 are the radii of the outer circle and the inner circle respectively. The area of a circular ring can be found by subtracting the area of the smaller (inner) circle from that of the larger (outer) circle.
Area of a ring
= Area of the larger circle – Area of the smaller circle
= πR12 – πR22
= π(R12 – R22)
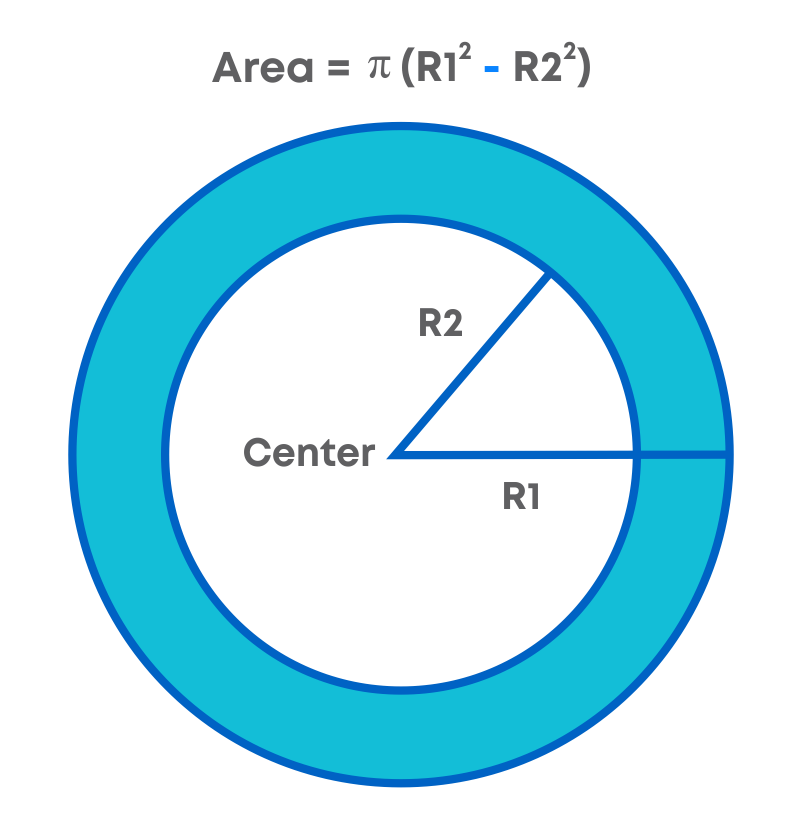
Where R1 = outer radius and R2 = inner radius.
To solve problems on finding the area of the path between 2 circles, follow the strategy given below.
- Identify or find the radius of the outer and inner circles.
- Calculate the area of the inner circle and the outer circle.
- Subtract the area of the inner circle from the area of the outer circle to find the area between the 2 circles.
To compare the area of a circle and the area of a rectangle when the circumference of the circle is equal to the perimeter of the rectangle:

- To find the area of the circle: Using the circumference calculate the radius and then find the area
- To find the area of the rectangle: Using the perimeter and the given one side, calculate the other side and then find the area.
Perimeter and Area
Let us learn how to convert units to other units while measuring areas.

You can find that this square of side 1 cm can be divided into 100 squares, each side 1 mm.
Area of a square of side 1 cm = Area of 100 squares of each side 1mm.
Therefore, 1 cm2 = 100 × 1 mm2 or
1 cm2 = 100 mm2
Similarly, 1 m2 = 1 m × 1 m
= 100 cm × 100 cm (As 1 m = 100 cm)
= 1000 cm2
In the metric system, areas of land are also measured in hectares [written “ha” in short]. A square of side 100 m has an area of 1 hectare.
So, 1 hectare = 100 × 100 m2
= 10,000 m2
You must have observed that quite often, in gardens or parks, some space is left all around in the form of a path or in between as cross paths.
A framed picture also has some space left all around it.

We need to find the areas of such pathways or borders when we want to find the cost of making them.
To solve problems on finding the area between 2 rectangles follow the given strategy
- Find the area of the outer rectangle and the inner rectangle
- Subtract the area of the inner rectangle from the area of the outer rectangle to find the area between them.
Common Errors
The following are topics in which students make common mistakes when dealing with perimeter and area:
- 1. Area of a triangle
- 2. Area of a triangle
- 3. Use the value of pi as directed in the question
- 4. Calculate the area of the shaded portion
Area Of A Triangle
Consider the given triangle. What is its area?
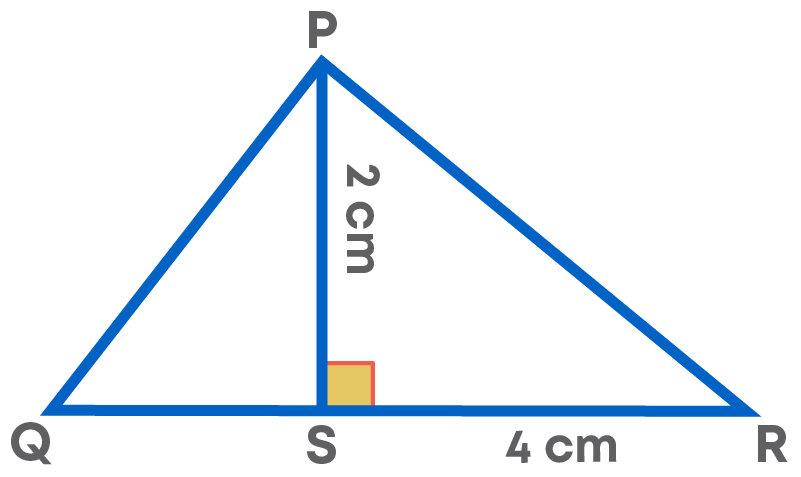
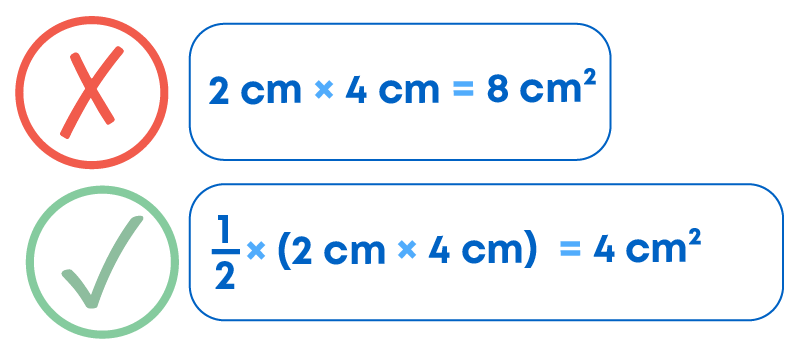
Sometimes, while calculating the area of a triangle we forget to multiply by half.
Remember:
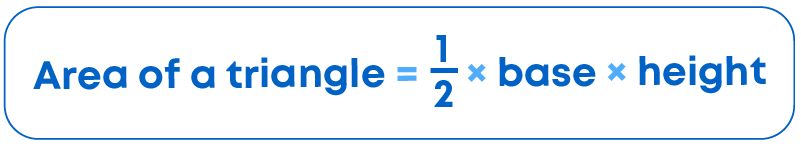
Area Of A Triangle
Identify the correct base and height pair in a triangle. Consider the given figure. Calculate the area of the triangle ABC.
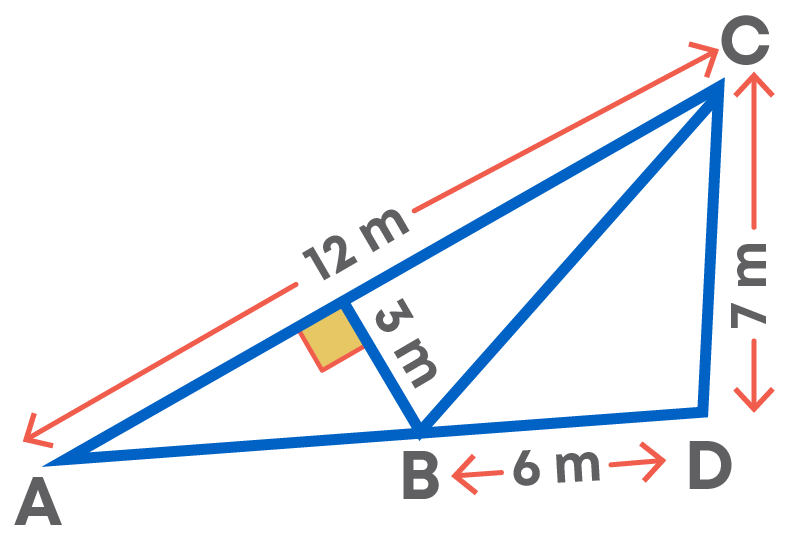
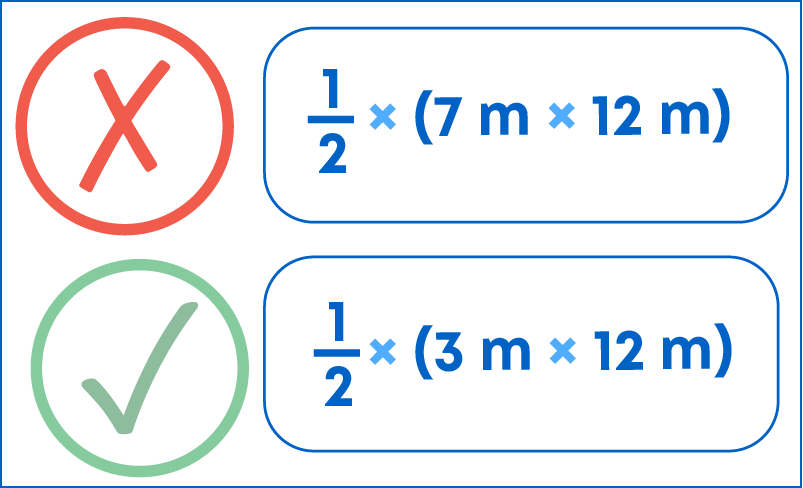
Here for triangle ABC, the correct pair of height and base,
- Base = 12 m
- Height = 3 m
Use The Value Of Pi As Directed In The Question
Usually, we take 4 values of pi,
- 3.14
- In terms of π
- Calculator value
- 22 2
However, in some questions, the value of pi to be considered is given:
1 .The radius of a circular pipe is 10 cm. What length of tape is required to wrap once around the pipe (π = 3.14)?
2. Find the perimeter of the given shape. (Take π = 22 7)
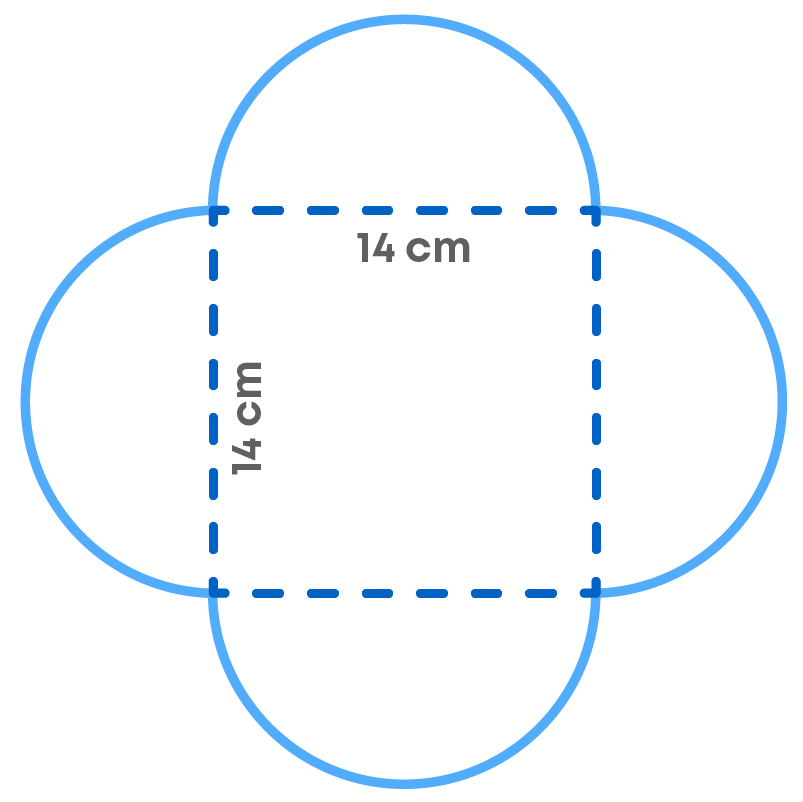
In the first question, we will use the value of π as 3.14 and in the second question, we use pi as 22/7. Why so? Because it is given in the question for easier calculation. Hence, be very careful while solving such questions.
Remark: So, we must use the value of π as mentioned in the question.
Calculate The Area Of The Shaded Portion
Observe the given question:
Two crossroads, each of width 5 m, run at right angles through the centre of a rectangular park of length 70 m and breadth 45 m, and parallel to its sides. Find the area of the roads.
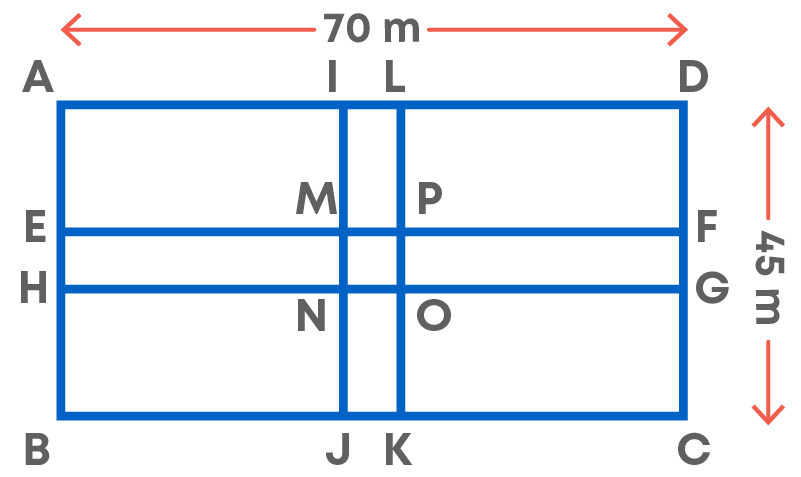

While solving such questions make sure that we subtract the area which is common in both the shapes.
Conclusion
The following table gives the length, breadth, and perimeter of some rectangles.
Fill in the blanks to find A, B, C, D, and E.





















































