Introduction
Fraction is a number representing equal parts of a whole. The whole may be a single object or a group of objects.

A pizza is cut into 8 equal pieces. You eat 3 pieces. The fraction of pizza that you ate can be represented by the fraction 3/8.
Let us look around and understand where we use fractions in real life. Watch the video below:
Now you have seen that fractions are used in many places around us. Can you think of some everyday activities in which you use the principles of fractions? If you are following a recipe you will come across measurements such as 14 tablespoon, 13 teaspoon, or ‘half a cup’. These are all fraction numbers, and it is important to know how to work with them. Further, if you want to make amends to the recipe, you will need to learn fractions.
For example, if a recipe for two people calls for 12 cup sugar but you are cooking for 4 people, you will have to double each ingredient, which means you will require 2 × 12 cup sugar.

Concepts
The chapter ‘Algebra’ covers the following concepts:
Fractions And Its Types

For example, look at this square. It is divided into 3 equal parts.

The fraction of the square that is coloured purple is 2/3. The fraction 23 has two parts - Numerator and Denominator.
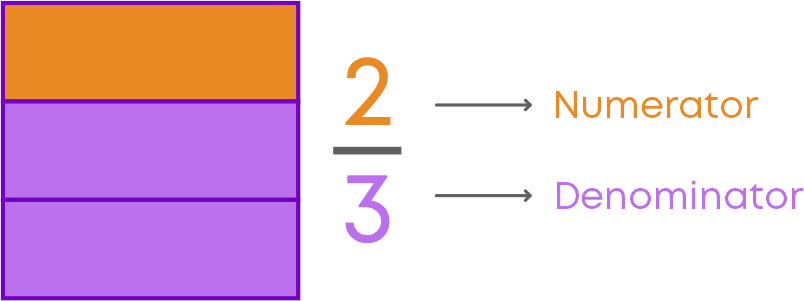
The numerator tells us the number of parts considered. In the example above, it is the number of parts that are purple in colour.
The denominator tells us the total number of equal parts in the whole. This is the total number of parts the square is divided into.
We can identify fractions represented in the form of figures. Consider the figure given below:
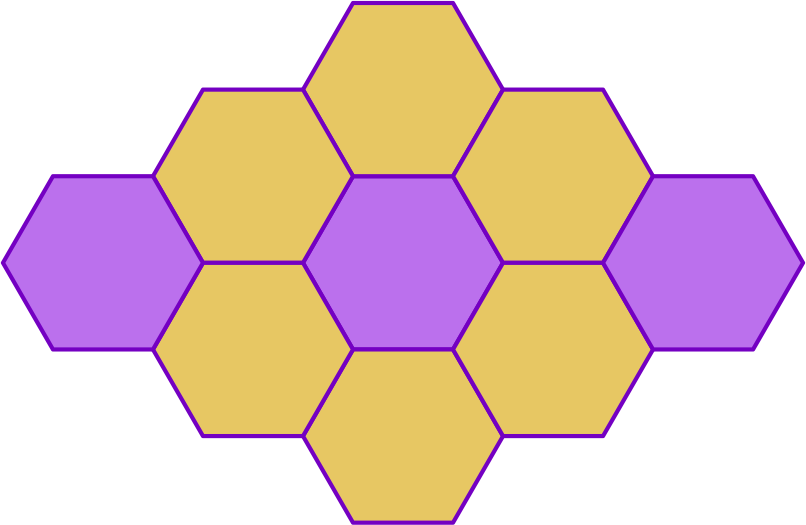
You can see that a pattern is made using hexagons of the same size. There are 9 hexagons in total. This forms the denominator of the fraction. Out of 9 hexagons, 3 are coloured as purple and 6 are coloured as yellow. This forms the numerator of the fractions. Let us try to identify the fraction of each colour.
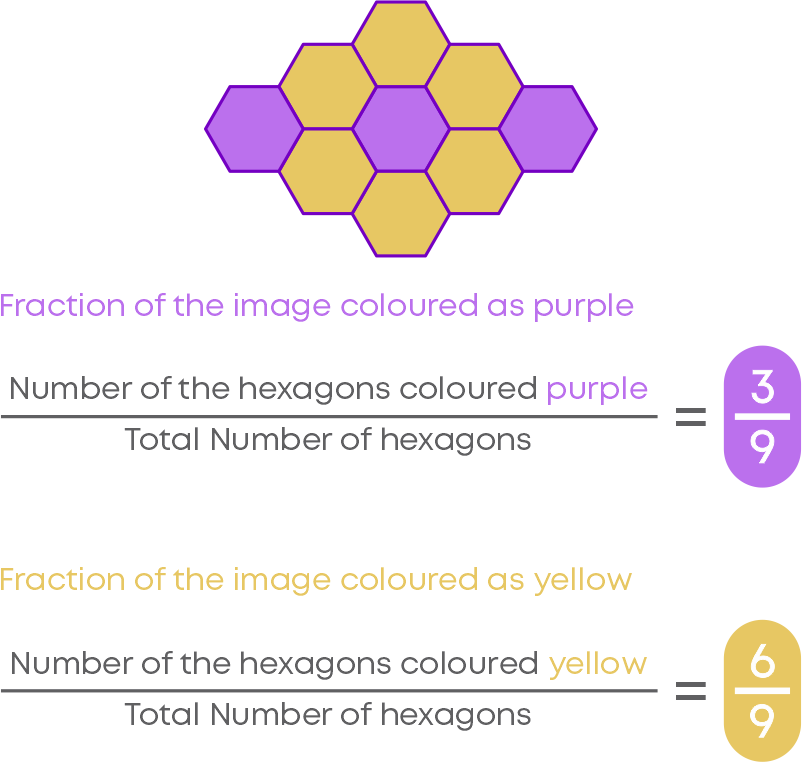
Hence, we can identify the fractions represented by the shaded portion of any figure as follows:
The total number of equal parts of the figure gives the denominator of the fraction. The number of shaded parts gives the numerator of the fraction.
We can also identify fractions from real-life situations by finding the total number of parts and finding the number of parts considered. Then, write the required fraction as number of parts considered / total number of parts
While representing fractions through geometric figures, the strategy is to choose the right figure as a whole. Choosing the right geometric figure helps to divide the whole into equal parts easily. Care should be taken that the figure is divided into equal parts.
- Square and rectangles can be used for any denominators.
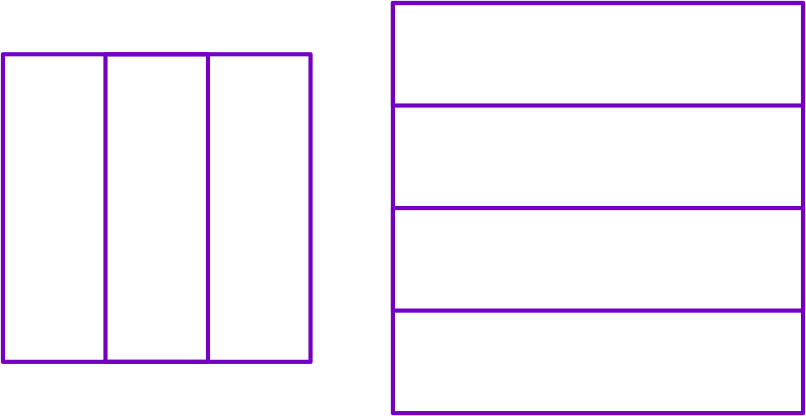
- If the denominator is 5, 7 etc., you may choose the whole as a polygon.
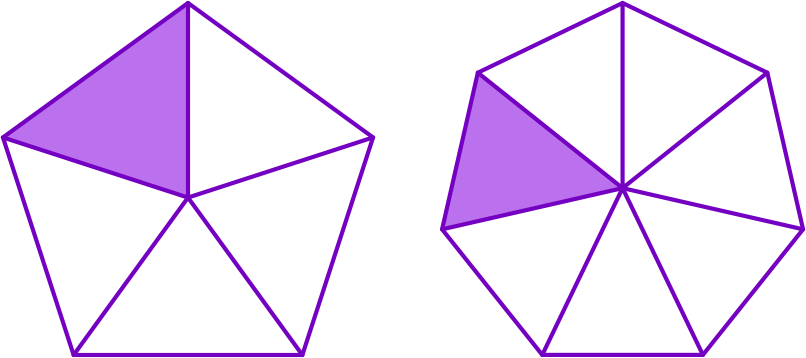
- For rectangular numbers like 8, 15 etc., choose the whole as a rectangle.
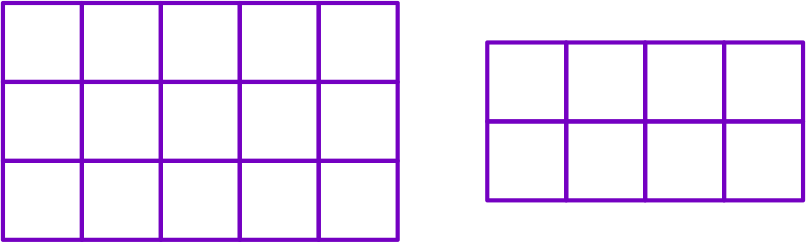
Once you have your chosen geometric shape to represent a fraction, divide it into the number of equal parts as in the denominator. Then, shade the number of parts as in the numerator. For example, 2/5 can be represented as

You know how to write fractions from real-life situations. Let us now understand how to express a given verbal expression as fractions. First, find the number of parts considered. Required fraction = number of parts considered / total number of parts.
Then, look out for keywords like ‘remaining’, ‘left’, ‘twice,’ etc.
Left means
- ‘Remaining’
- ‘The less that is available’
For example, due to heavy rains, most of the children were absent, so there were a few children left in the class.
Example: Radhika has a chocolate bar with 12 pieces. She ate 3 pieces. Her sister ate 5 pieces. What fraction of chocolate was left?
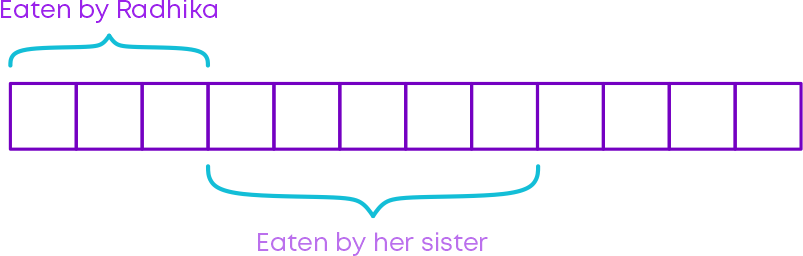
Number of pieces left = 12 – (3 + 5)
= 12 – 8
= 4
Hence, the fraction of chocolate left = 4 / 12.
Let us learn some other terms used in fractions:
Twice means
- ‘Double’
- ‘Multiplied by two’
For example, when the answer was wrong, the teacher asked Raju to write the answers twice in his notebook.
As much as means
- The same amount
- An equal amount
Let us now try to identify fractions on the number line. Consider the number line given below.

We can see that the length between ‘0’ and ‘1’ is divided into three equal parts. The first division represents the fraction 1/3. The second division represents the fraction 2/3. Also, note that ‘0’ represents the fraction 0/3 and'1'is the third division, hence, it represents the fraction3/3.
To identify fractions on a number line,
- Find how many equal parts is the length between ‘0’ and '1' divided into. This forms the denominator of the fraction.
- Identify the part where the fraction lies. This forms the numerator of the fraction.
Remember, between ‘0’ and '1' there are infinite number of fractions.
You know how to identify fractions from a given number line. Let us now see how to represent fractions on the number line. Let us represent the fraction 15 on the number line following these steps:
- 1. Draw the number line.
- 2. 1/5 is greater than ‘0’ and less than 1. Also 1/5 means 1 part out of 5 equal parts. Hence, divide the length between ‘0’ and 1 into 5 equal parts.
- 3. Mark the 1st division as 1/5.
- 4. Mark the subsequent divisions as 2/5, 3/5, and 4/5.
The fractions marked on the number line is as follows.
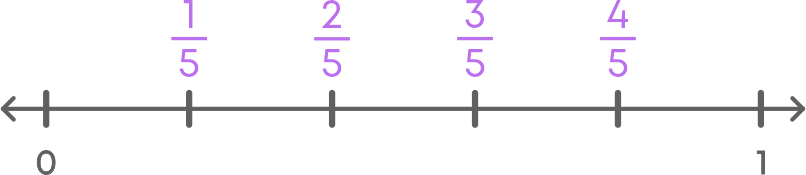
Let us now learn about the different types of fractions.
A fraction whose numerator is less than the denominator is called a proper fraction. All proper fractions are less than 1. For example, 7/8, 3/4, and 1/6 are proper fractions and they are less than 1.
A fraction whose numerator is greater than the denominator is called an improper fraction. All improper fractions are greater than 1. For example, 5/4, 10/7, and 11/6 are improper fractions and they are greater than 1.
A mixed fraction has a combination of a whole and a part. All mixed fractions are greater than 1. For example, 1 1/3, 2 3/5, and 11 5/6 are mixed fractions and they are greater than 1.
Fractions having the same denominators are called like fractions. Example, 1/8, 2/8, 3/8, 4/8, etc.
Fractions having different denominators are called unlike fractions. Example, 1/3, 2/5, 3/4, 4/8, etc.
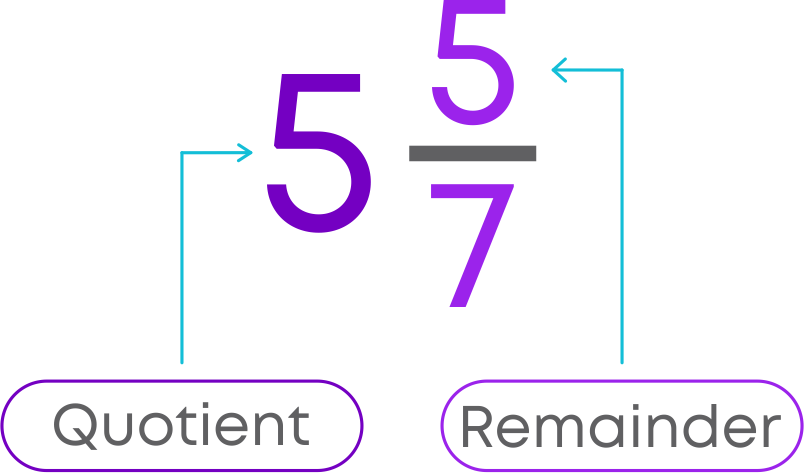
Let us understand how to convert improper fractions to mixed fractions. Let us convert the improper fraction 65/9 to a mixed fraction.
First, perform long division method to divide 65 by 9. Identify the quotient and the remainder.

As you know mixed fraction is a combination of a whole number and a fraction.
- Write the quotient as the whole number.
- Write remainder / denominator as the fraction.
Mixed fraction = Quotien tremainder / denominator
Hence, mixed fraction of 65/9 is 7 2/9.
Let us see how to convert mixed fractions to improper fractions. Let us find the improper fraction of 5 5/7.
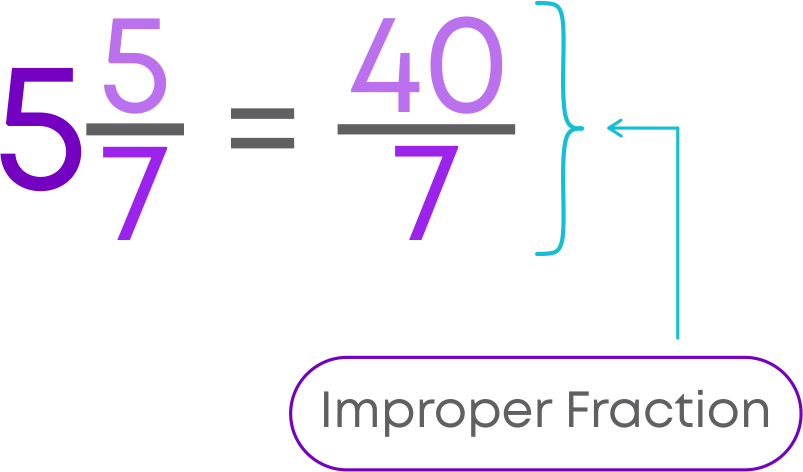
To convert mixed fractions to improper fractions, follow these steps:

Equivalent Fractions
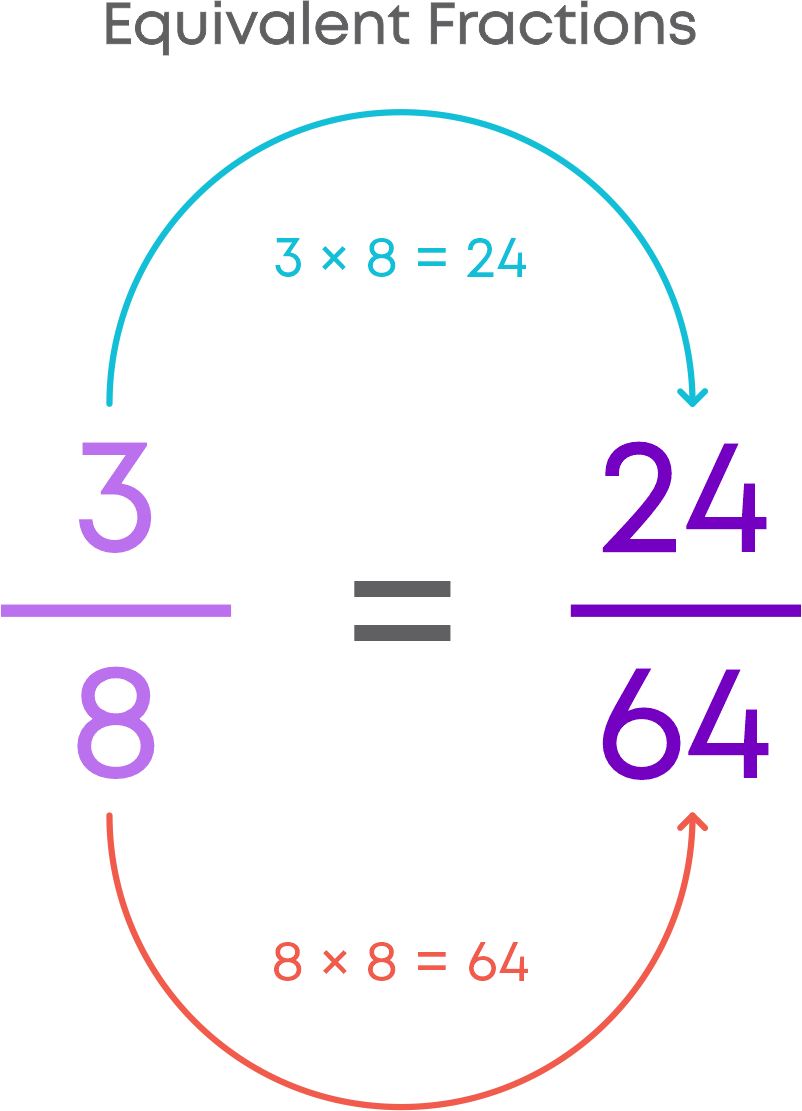
Equivalent fractions are fractions with different numerators and denominators but represent the same value or proportion of the whole. For example, 1/3, 2/6, 3/9 are equivalent fractions. We will now learn how to find equivalent fractions of a given fraction by multiplication. Let us find the equivalent fraction of 2/3.
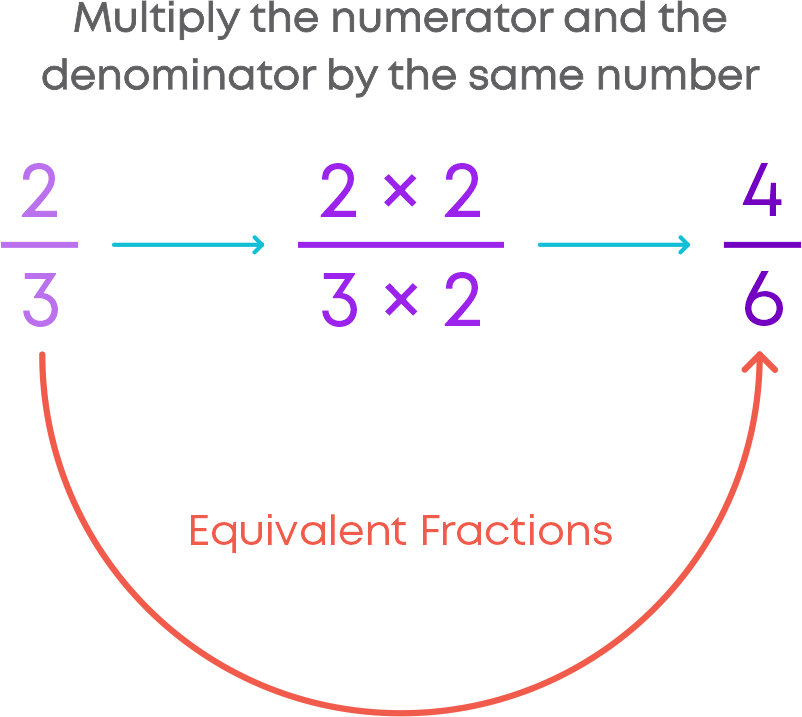
To find the equivalent fraction of a given fraction, multiply both the numerator and the denominator of the given fraction by the same number.
We can also find equivalent fractions using the division method. Consider 1830.

To find the equivalent fraction of a given fraction, divide both the numerator and the denominator of the given fraction by the same number.
We can find an infinite number of equivalent fractions for a given fraction. Remember to multiply or divide the numerator and the denominator by the same number.
For equivalent fractions, the product of the numerator of the first fraction and the denominator of the second fraction is equal to the product of the denominator of the first fraction and the numerator of the second fraction. These products are called cross-products.
To check if the given pair of fractions are equivalent, follow these steps.
- Find the cross-products.
- If the cross-products are equal, then the fractions are equivalent.
- If the cross-products are not equal, then the fractions are not equivalent.

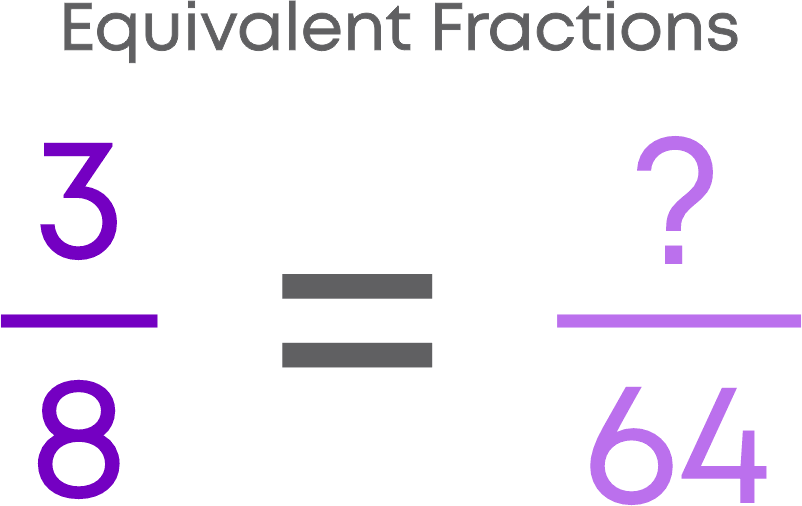
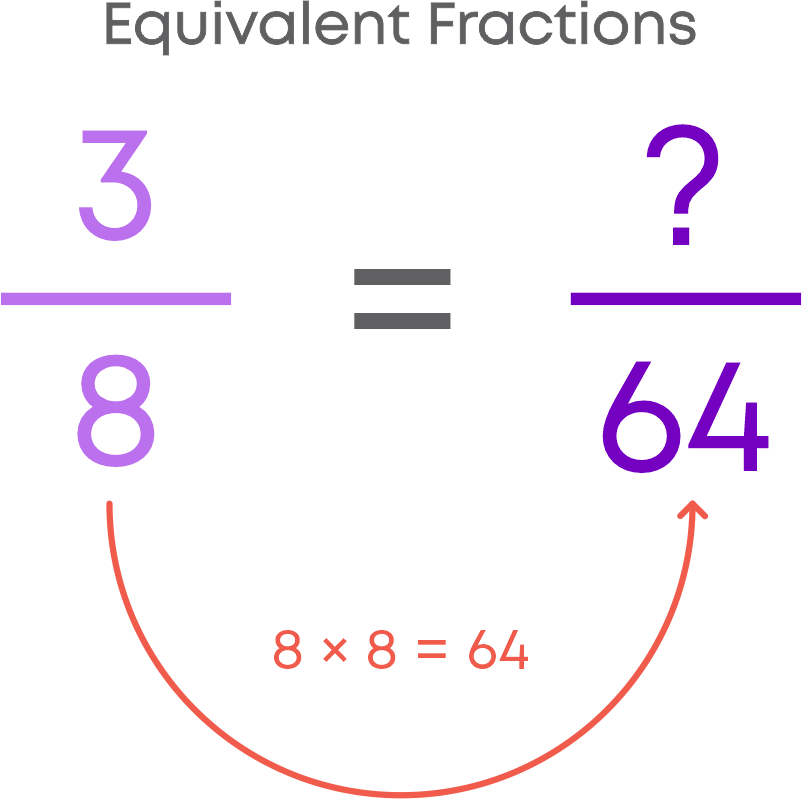
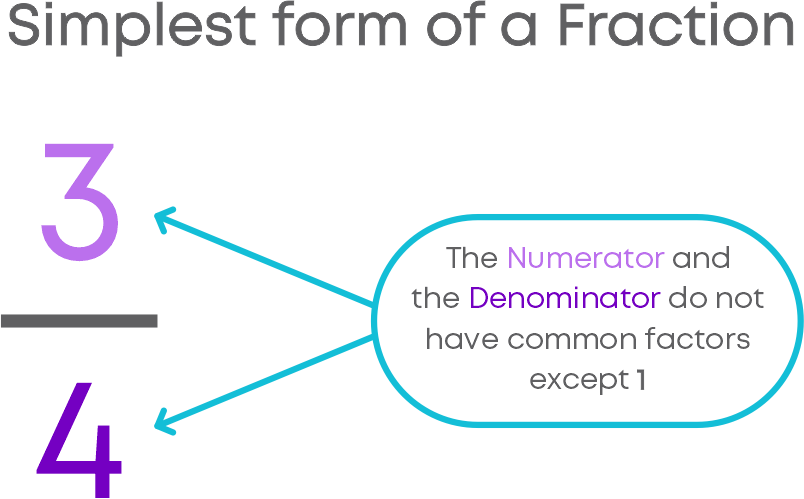
Simplest Form Of A Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1.
To convert a fraction (for e.g., 24 / 36) to its simplest form, follow these steps:
-
Find the HCF of the numerator and denominator.
24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3 × 3
HCF of 24 and 36 is 2 × 2 × 3 = 12 - Divide the numerator and denominator by the HCF.
24 ÷12 / 36 ÷12 = 23
Hence, the simplest form of 2436 is 23.
Comparing And Ordering Fractions
To compare like fractions,
- Identify the numerators of the like fractions.
- For two fractions with the same denominator, the fraction with the greater numerator is greater.
Consider these fractions:

In both the fractions, the whole is divided into 10 equal parts. For 710 and 910 we take 7 and 9 parts respectively out of the 10 equal parts.
Since 9 > 7, 9 / 10 > 7 / 10
As you know, ordering fractions means arranging them in ascending or descending order. Let us learn how to order like fractions.

The same fractions in descending order:

Now, to compare unlike fractions, follow these steps:
- Find the LCM of the denominators.
- Convert each fraction to an equivalent fraction with denominator as the LCM obtained.
- Compare the numerators of the like fractions obtained.
To arrange unlike fractions in ascending or descending order, start again by taking the LCM of the denominators, converting each fraction to an equivalent fraction with denominator as the LCM obtained, and then comparing and ordering the numerators of the like fractions obtained.
Operations On Fractions
We can add like fractions by representing them using figures. To add like fractions, add the numerators and retain the common denominator. To add two unlike fractions we follow these steps:
Consider 5 / 9 and 7 / 12.
LCM of 9 and 12 is 36. The equivalent fraction of 5 / 9 with denominator 36 is 5 ×4 / 9 ×4 = 20 / 36.
The equivalent fraction of 7 / 12 with denominator 36 is 7 × 3 / 12 ×3 = 21 / 36.
20 / 36 + 21 / 36 = 41 / 36 = 1 5 /36
Hence, the sum of 5 / 9 and 7 / 12 is 1 5 / 36.
Now, consider that Santosh has 9/12 of a pizza. He gave 5/12 of the pizza to his children. What is the fraction of pizza left with him?

We must subtract 9 / 12 – 5 / 12
= 4 / 12
To subtract two unlike fractions, follow the same steps as before, by finding the LCM of the denominators and converting the fractions to like fractions to subtract.
We can find the missing fractions in addition or subtraction statements. For example:
1 / 3 + __ = 5/6
Here, the missing fraction is 5/6 – 1/3 = 5-2 / 6 = 3/6 = 1/2
We can use addition and subtraction of fractions to solve different types of problems.
- To find the fraction to be added or subtracted to get a required sum, we must subtract the smaller fraction from the larger fraction.
- To find the third fraction in the sum of three fractions, we must subtract the sum of the two fractions from resultant fraction.
While solving word problems on addition and subtraction on fractions, look out for the keywords.
If the question has keywords like ‘total’, ‘altogether’, ‘in all,’ then perform addition.
If the question has keywords like ‘left’, ‘remaining’, ‘how much more/less,’ then perform subtraction.
Common Errors
The following are the topics in which students make common mistakes when dealing with fractions
- 1. Convert Mixed Fractions to Improper Fractions
- 2. Convert the Given Fraction to its Simplest Form
- 3. Comparing Unlike Fractions
- 4. Addition of Like Fractions
- 5. Addition of unlike fractions
- 6. Subtraction of Fractions
Convert Mixed Fractions to Improper Fractions
To convert mixed fractions to improper fractions, we follow this formula.

For example, let us convert the mixed fraction 4 3/5.
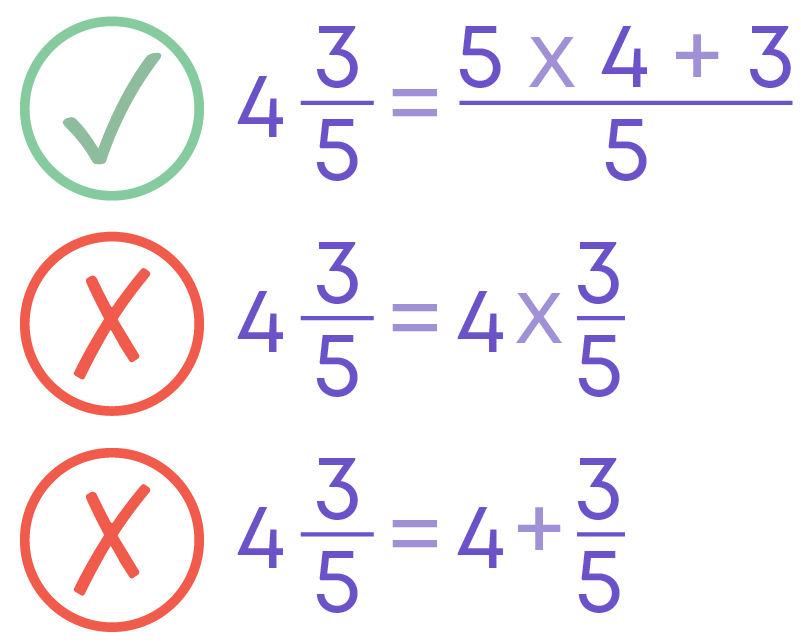
Convert the Given Fraction to its Simplest Form
To convert the given fraction to its simplest form we follow these steps:
- Find the HCF of the numerator and the denominator.
- Divide the numerator and the denominator by the HCF.
- The resultant fraction is the simplest form of the given fraction.
For example, et us find the simplest form of the fraction 36 / 96.
HCF of 36 and 96 is 12. 36 / 96 = 36 ÷ 12 / 96 ÷12 = 3/8
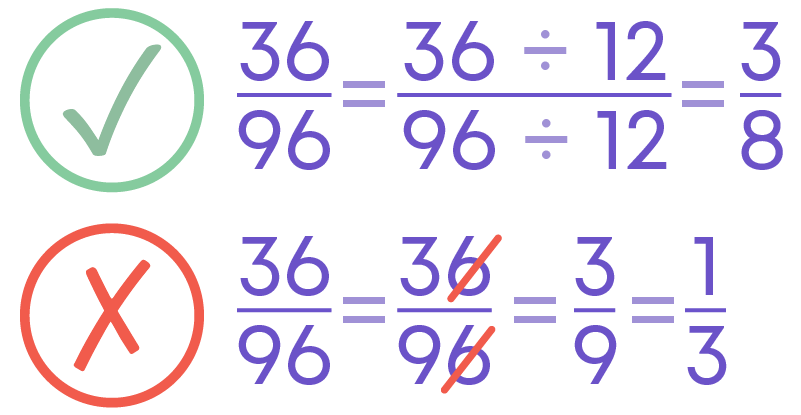
Comparing Unlike Fractions
To compare the unlike fractions, we follow these steps:
- Find the LCM of the denominators of both fractions.
- Convert each of the fractions as an equivalent fraction with the denominator as the LCM.
- Compare the numerators of the equivalent fractions.
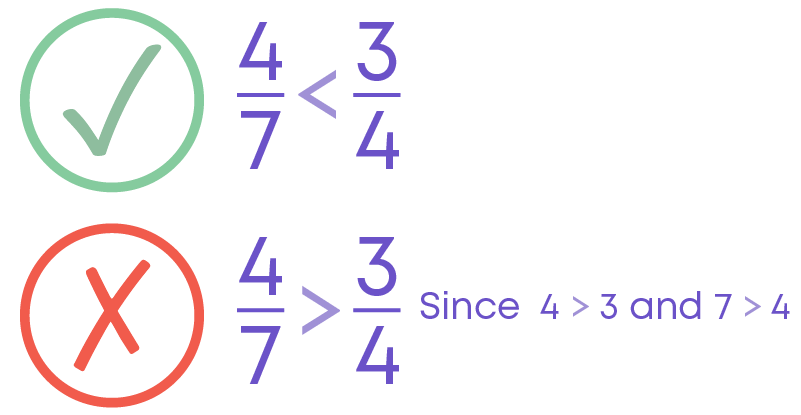
Addition of Like Fractions
To add like fractions,
- Add the numerators and retain the common denominator.
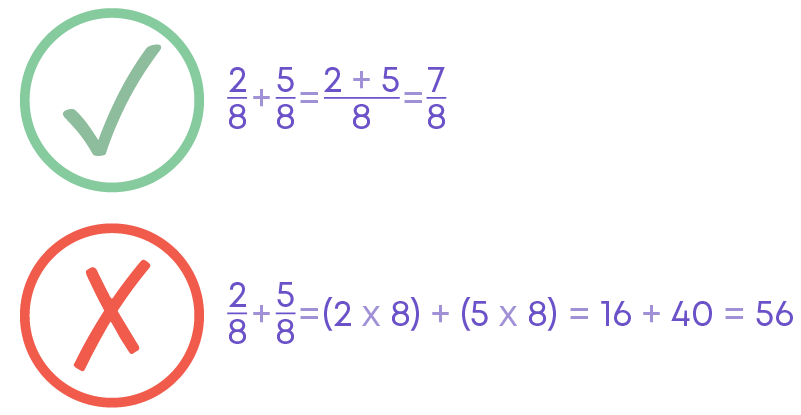
Addition of unlike fractions
To add unlike fractions,
- Find the LCM of the denominators.
- Convert each fraction into an equivalent fraction with the denominator as the LCM obtained.
- Add the numerators and retain the common denominator.
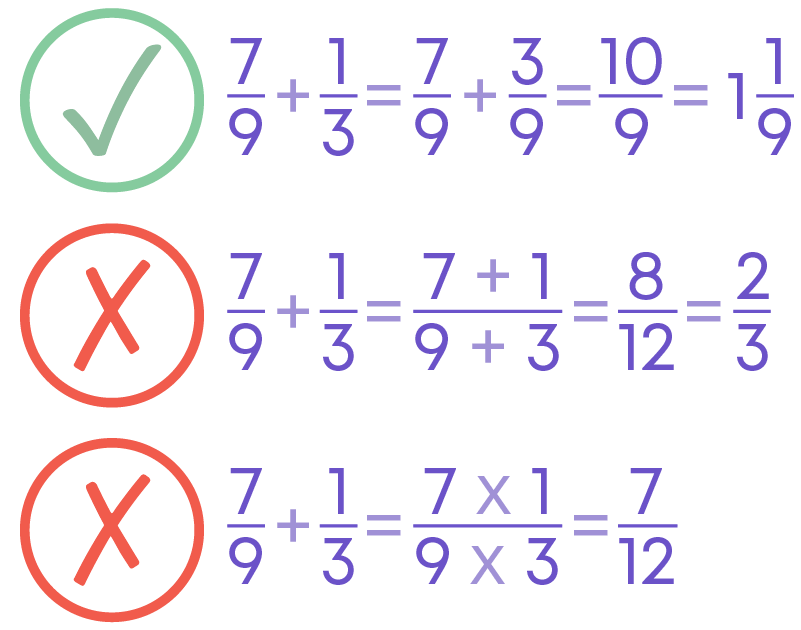
Subtraction of Fractions
To subtract fractions:
- Find the LCM of the denominators.
- Convert each fraction to an equivalent fraction with the denominator as the LCM obtained.
- Subtract the numerators and retain the common denominator.
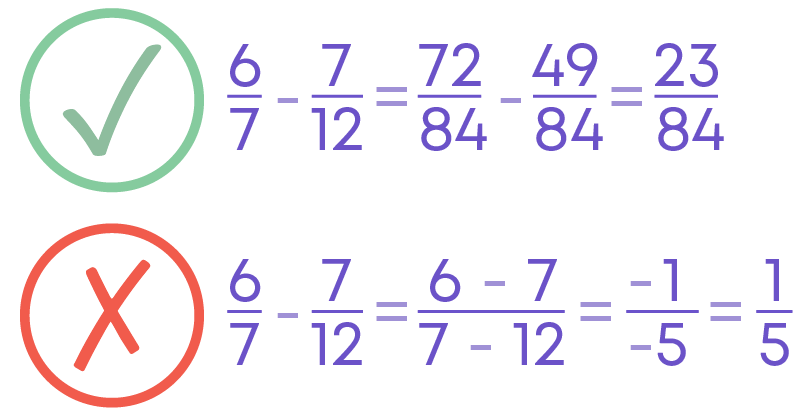
Conclusion
Fractions are an interesting and significant part of maths. Try to solve this riddle based on fractions below:
I am a city. I am 2/7 of a chicken, 2/3 of a hen, ¼ of a newt, and 2/3 of the air. Guess who I am.




















































