Introduction
We use the concept of lines and angles in nearly every aspect of our daily lives. We see lines on zebra crossing, windowpanes, doors, railway tracks, etc.

Angles used in building constructions make the difference of whether the building is safe or not, whether it stands upright and allows rainwater to run off the roof or not, etc.
So, architects and contractors need to calculate the angles very precisely.

Also, lines and angles are inter-connected with subjects like physics, chemistry etc.
What are the properties of angles formed when two lines intersect each other, or a line intersects two or more parallel lines at distinct points? Why it is very important to learn about lines and angles?
Let us watch this video to know about these.
Now, you know why we should learn lines and angles.
In this blog, we will learn more about the properties of the angles formed when two lines intersect each other, and the properties of the angles formed by a line intersecting two or more parallel lines at distinct points.
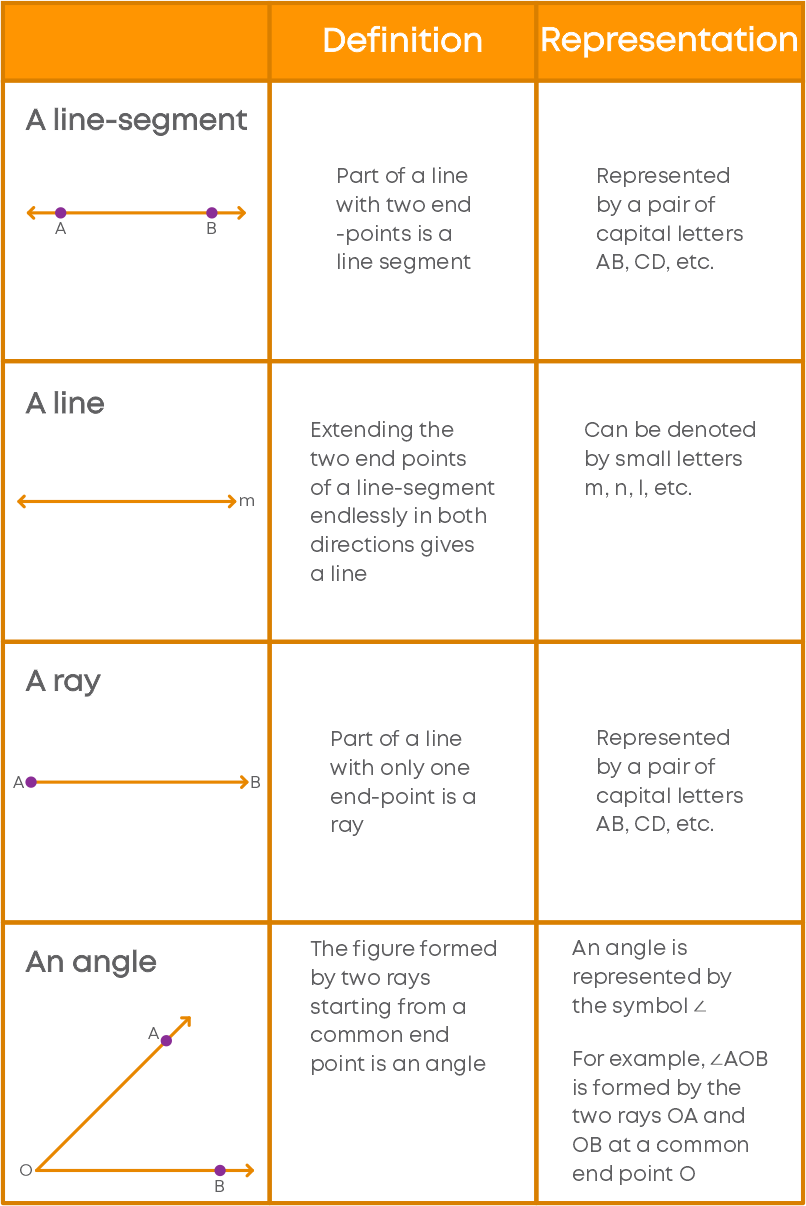
Now let us see the definitions of some basic geometrical shapes:
Let us see the types of angles based on their measures.

The following are the pair of angles that you know so far:
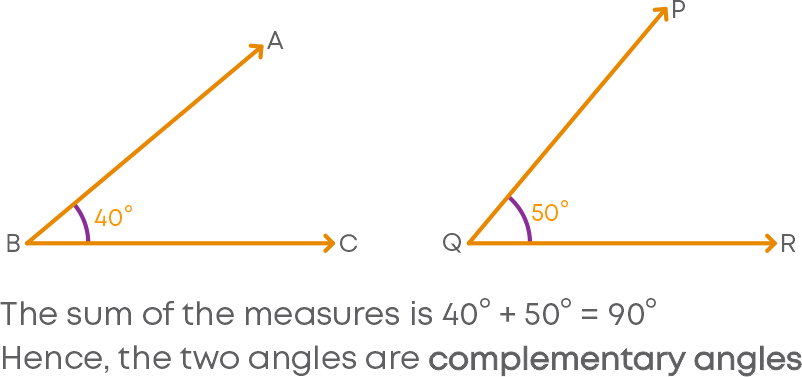
1. Complementary angles
Property of angles: Pair of angles whose sum is 90⁰. Example:
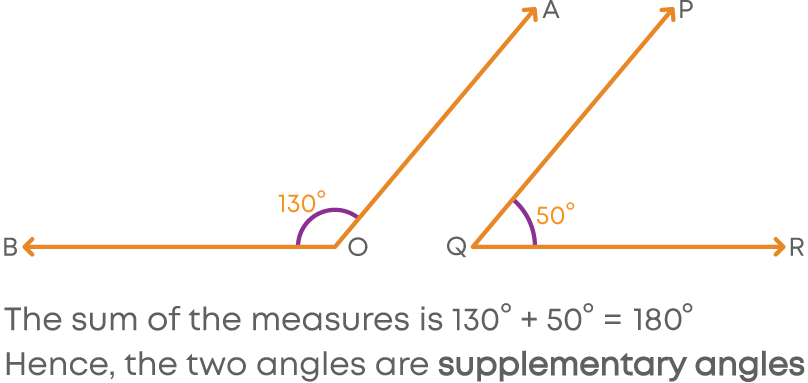
2. Supplementary angles
Property of angles: Pair of angles whose sum is 180⁰. Example:
3. Adjacent angles
Property of angles: Pair of angles having a common vertex and a common arm. Example:
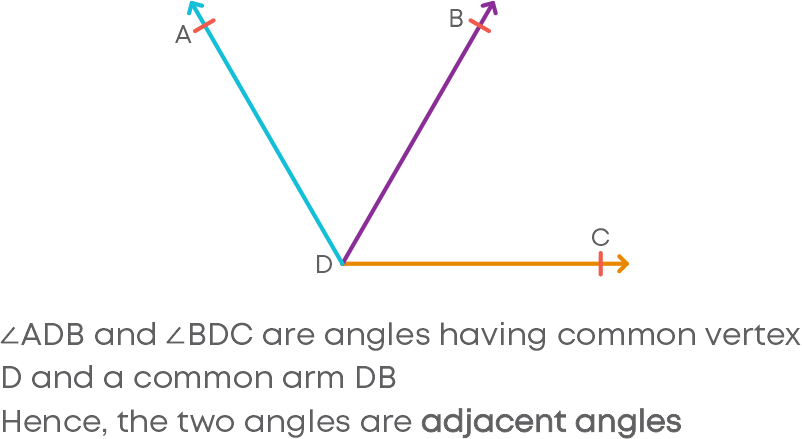
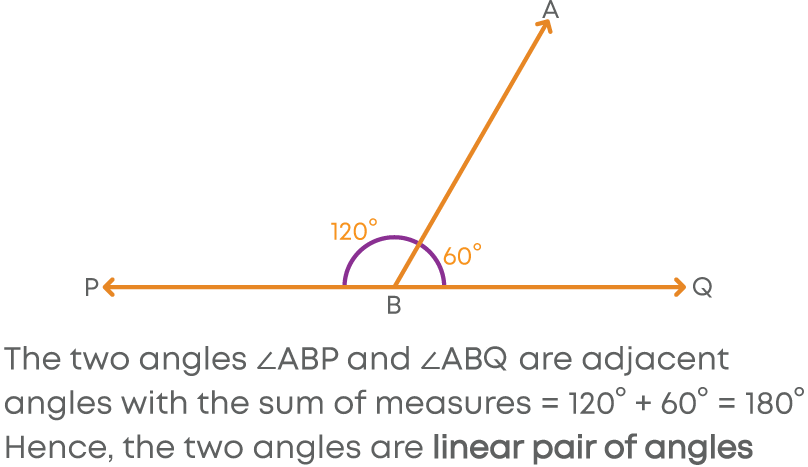
4. Linear pair of angles
Property of angles: Adjacent angles whose sum is 180⁰. Example:
5. Vertically Opposite angles
Property of angles: Opposite angles formed when two lines intersect each other. Example:
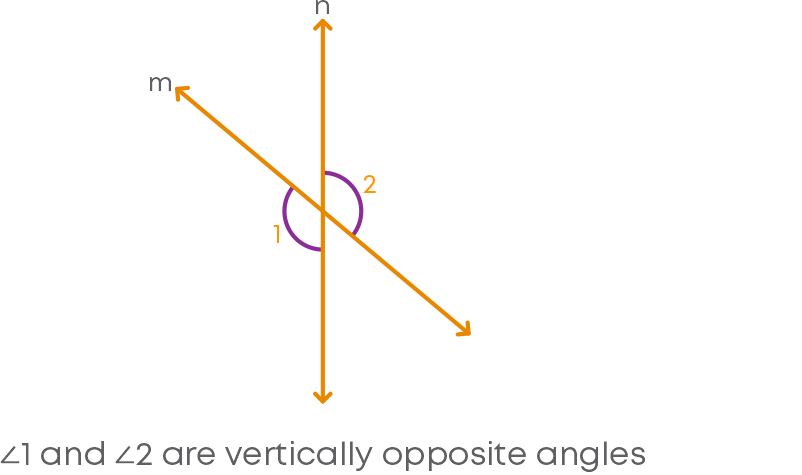
Let us look at the relation between some of these pairs of angles.
- Adjacent angles can be complementary angles.
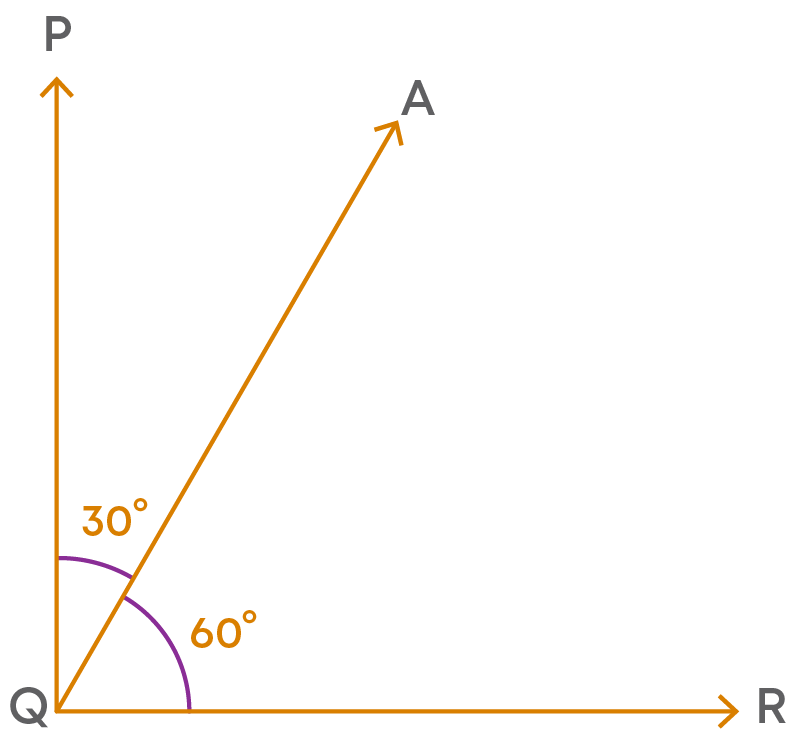
Here, ∠PQA and ∠AQR are adjacent angles as they have a common vertex Q and common arm QA. Also, the sum of the measures of these angles is
∠PQA + ∠AQR = 30⁰ + 60⁰ = 90⁰
So, they are complementary angles.
- Adjacent angles can be supplementary.
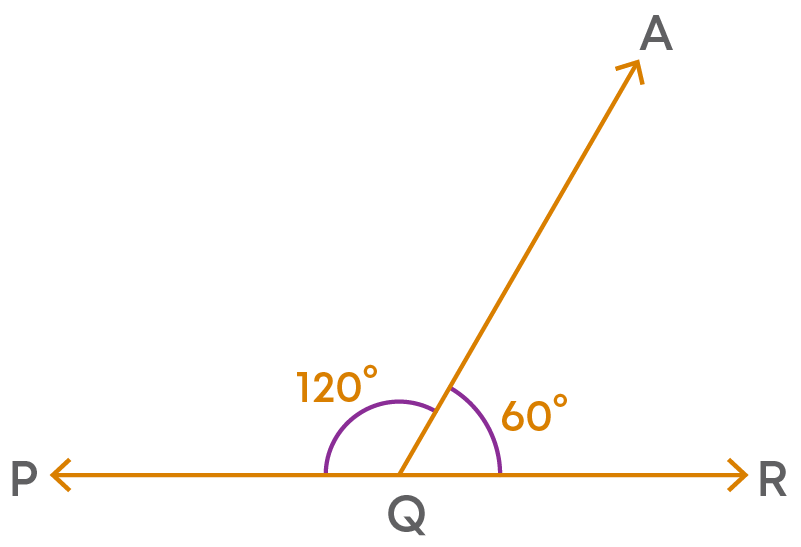
Here, ∠PQA and ∠AQR are adjacent angles as they have a common vertex Q and common arm QA. Also, the sum of the measures of these angles is
∠PQA + ∠AQR = 120⁰ + 60⁰ = 180⁰
So, they are supplementary angles.
Concepts
The chapter ‘Lines and Angles’ covers the following concepts:
Pairs of Angles
Consider:
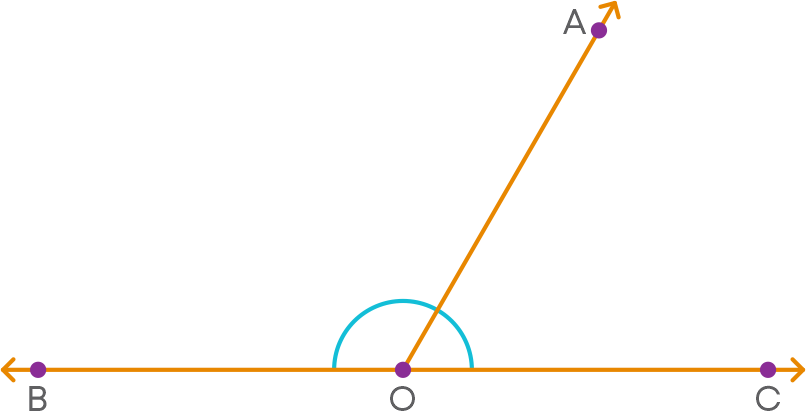
Here, ray OA stands on the line BC. This means ∠AOB and ∠AOC are adjacent angles such that ∠AOB + ∠AOC = 180⁰.
Hence, we can say that if a ray stands on a line, the sum of two adjacent angles so formed is 180⁰. This is axiom 1.
If the sum of two adjacent angles is 180⁰, what can we conclude about the non-common arms of these angles?
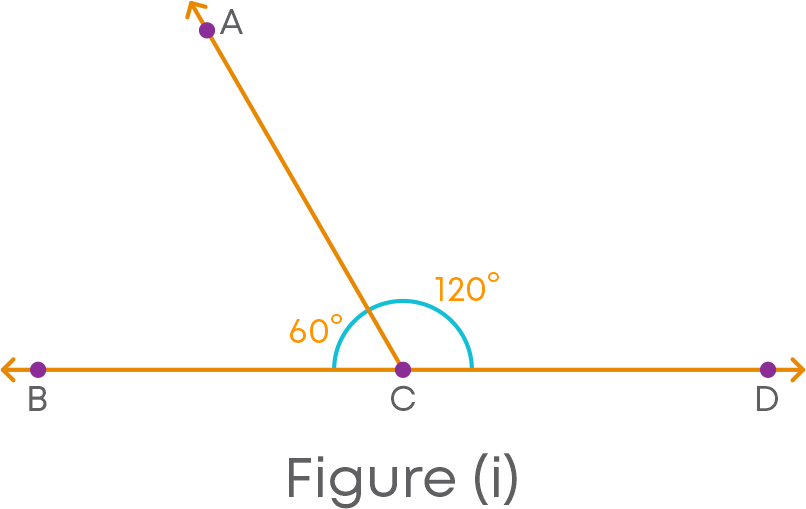
Here, we see that in figure (i), sum of the adjacent angles ∠ACB and ∠ACD is 180⁰.
i.e., ∠ACB + ∠ACD is 180⁰
We can see that the non-common arms CB and CD of the angles ∠ACB and ∠ACD form a straight line BD.
Also, points B, C and D lie on the same line BD and ray CA stands on it.
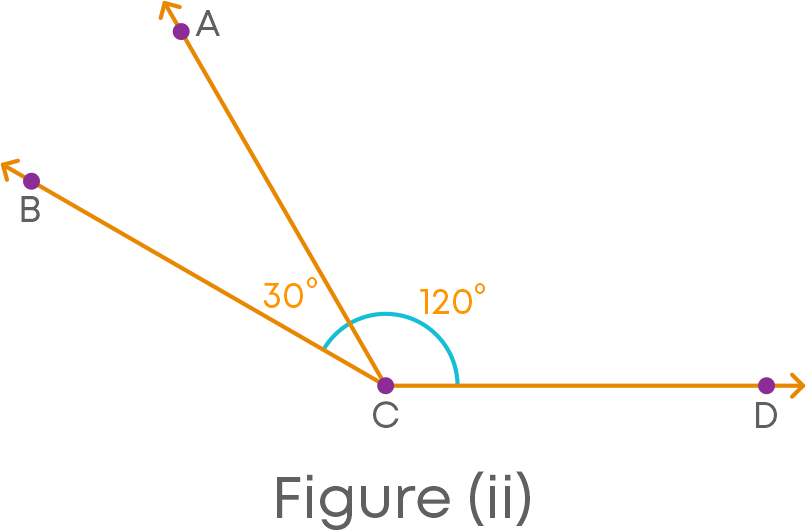
But, for figure (ii), sum of adjacent angles ∠ACB and ∠ACD is not 180⁰. ∠ACB + ∠ACD = 30 + 120 = 150⁰.
We can see that the non-common arms CB and CD of the angles ∠ACB and ∠ACD do not form a straight line.
So, we can say that the converse of the axiom ‘If a ray stands on a line, then the sum of two adjacent angles so formed is 180⁰’ is true.
Axiom 2: if the sum of two adjacent angles is 180⁰, then the non-common arms of the angles form a line.
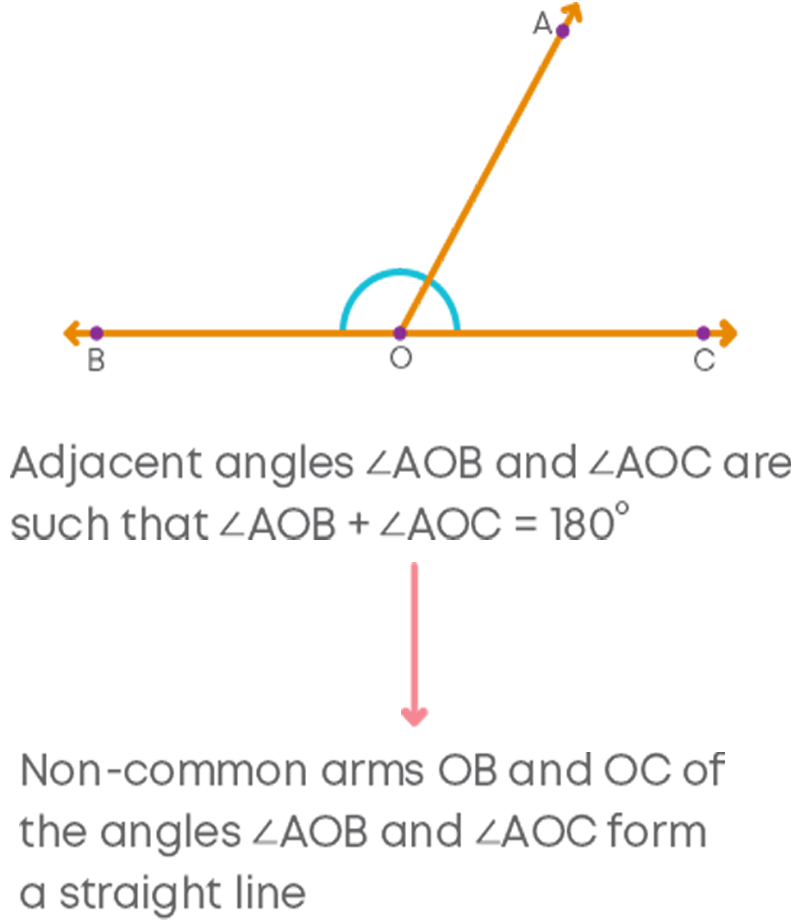
The two axioms above are together called as linear pair axiom.
The angles addition postulate states that when two or more angles have common arms, then the measure of the greatest angle is the sum of the measures of smaller angles.
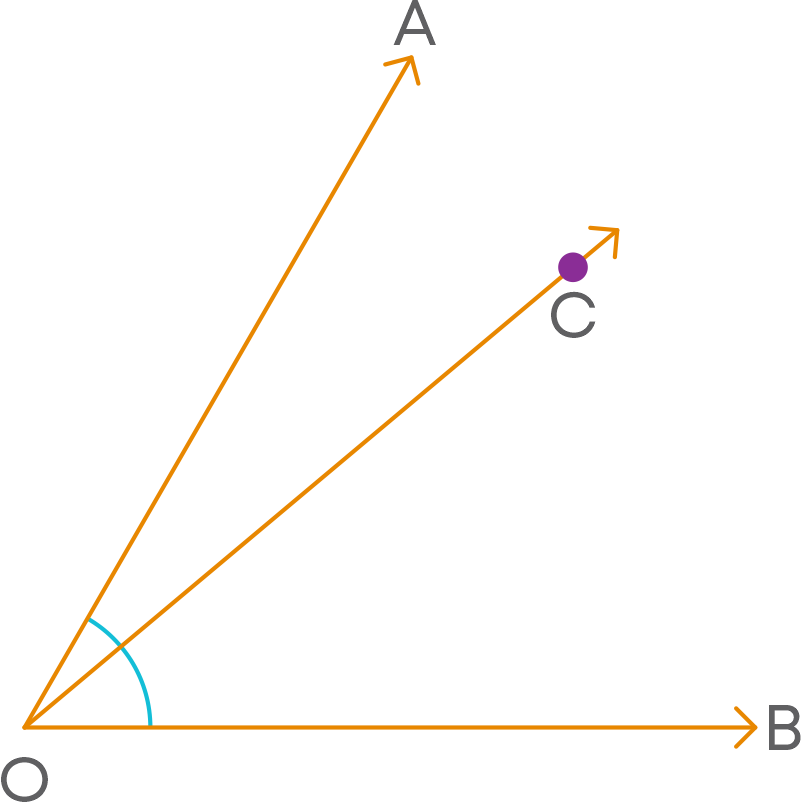
∠AOB = ∠AOC + ∠COB
We know that ‘If a ray stands on a line, then the sum of two adjacent angles so formed is 180⁰’. But what will happen if there is more than one ray?
Let us consider the figure below:
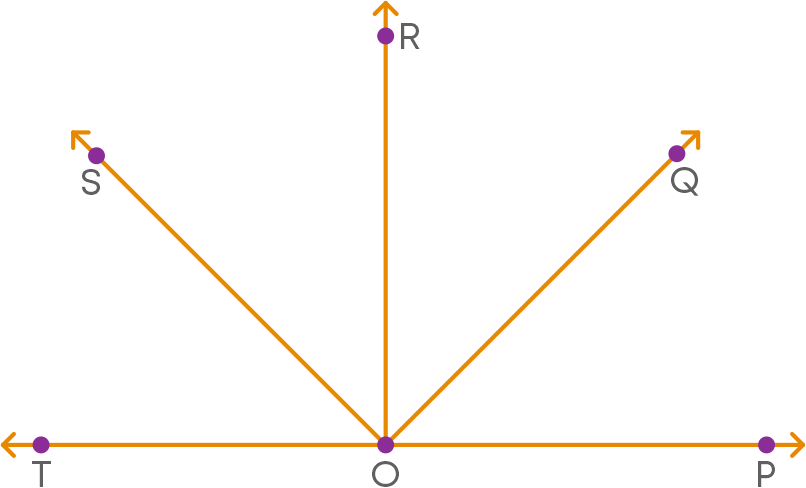
Here, the rays OS, OR, and OQ stand on straight line PT. What can you say about the sum of the angles ∠TOS, ∠SOR, ∠ROQ, and ∠QOP?
The sum of the angles ∠TOS, ∠SOR, ∠ROQ, and ∠QOP is 180⁰.
Theorem:
Sum of the angles on the same side of a line at a given point on the line is 180⁰.
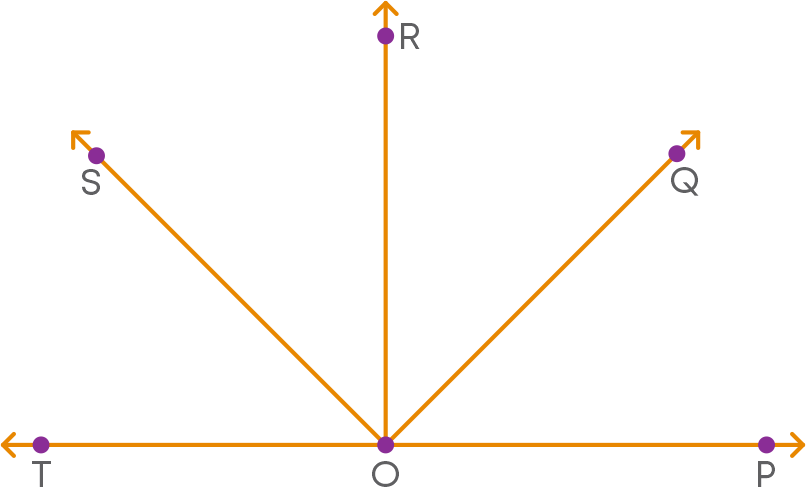
TOP is a straight line and rays OS, OR and OQ stand on it, forming ∠TOS, ∠SOR, ∠ROQ, and ∠QOP.
Ray OS stands on the line TP, hence, using linear pair axiom,
‘If a ray stands on a line, the sum of two adjacent angles so formed is 180 degrees’, we have
∠TOS + ∠SOP = 180⁰ -------- (i)
But ∠SOP = ∠SOR + ∠ROQ + ∠QOP
Substituting the above in the statement (i)
∠TOS + (∠SOR + ∠ROQ + ∠QOP) = 180⁰
The angles ∠TOS, ∠SOR, ∠ROQ, and ∠QOP are all angles at the point O and their sum is 180⁰.
Hence, it is proved that the sum of the angles on the same side of a line at a given point is 180⁰.


The sum of all angles around a point is 360⁰. Let us prove this with an example:
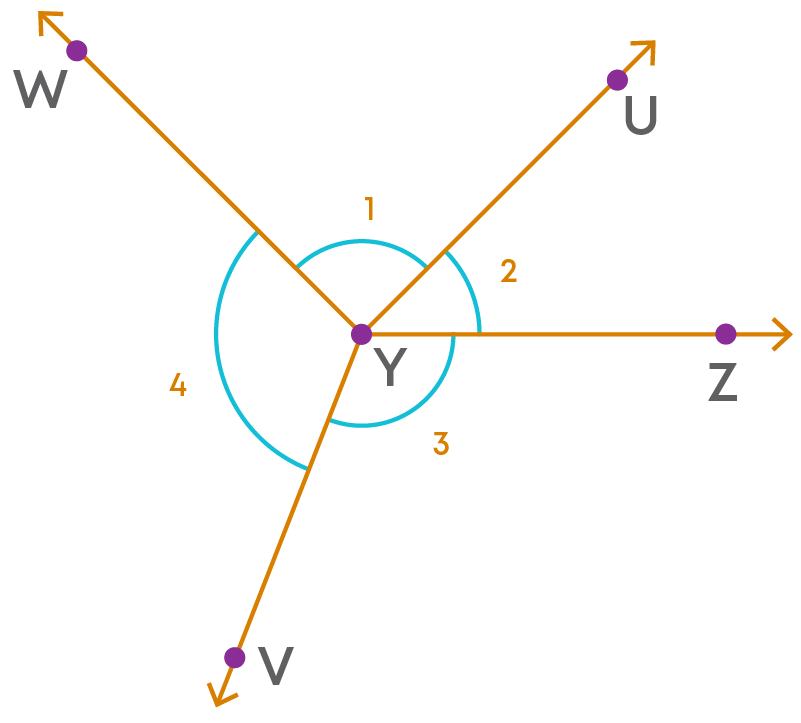
We are given a point Y and the rays YW, YU, YZ and YV make angles around the point Y.
First, produce ray YZ backwards to a point X such that XYZ is a straight line.
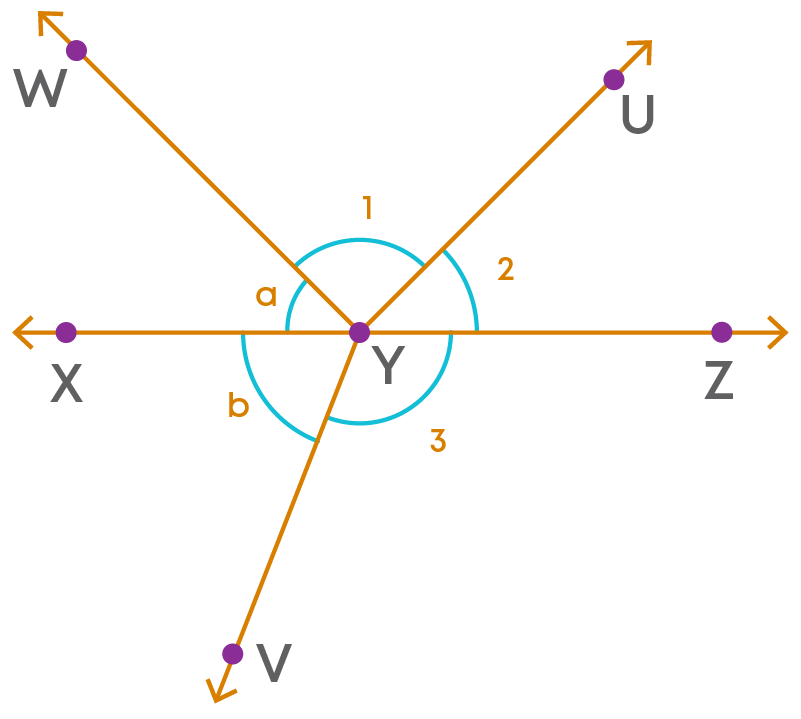
From the figure, we see that XYZ is a straight line. ∠a, ∠1 and ∠2 are on the same side of line XZ and formed at the point Y, hence, using the below theorem,
‘Sum of the angles on the same side of a line at a given point on the line is 180⁰.
We have ∠a + ∠1 + ∠2 = 180⁰ ------- (i)
Ray YV stands on the line XZ, hence, using the linear pair axiom,
‘If a ray stands on a line, the sum of two adjacent angles so formed is 180⁰.’
We have ∠b + ∠3 = 180⁰ ------- (ii)
Adding the corresponding sides of (i) and (ii), we get
∠a + ∠1 + ∠2 + ∠b + ∠3 = 360⁰
(∠a + ∠b) + ∠1 + ∠2 + ∠3 = 360⁰
∠4 + 1 + ∠2 + ∠3 = 360⁰
The angles ∠1, ∠2, ∠3, and ∠4 are all angles around the point Y and their sum is 360⁰.
Hence, the sum of all angles around a point is 360⁰.
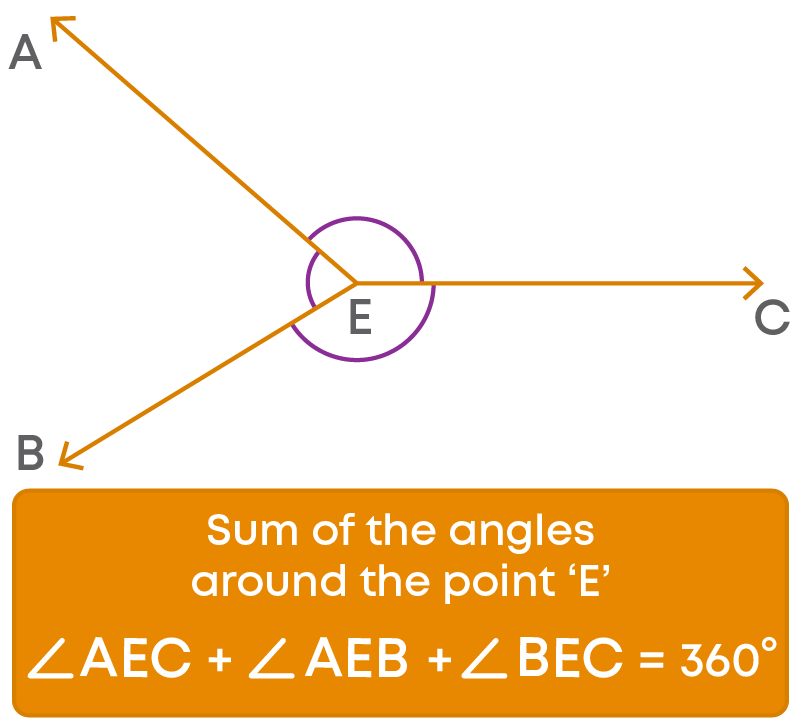

Let us look at an application of the linear pair axiom.
Let PQ be the surface of a mirror.
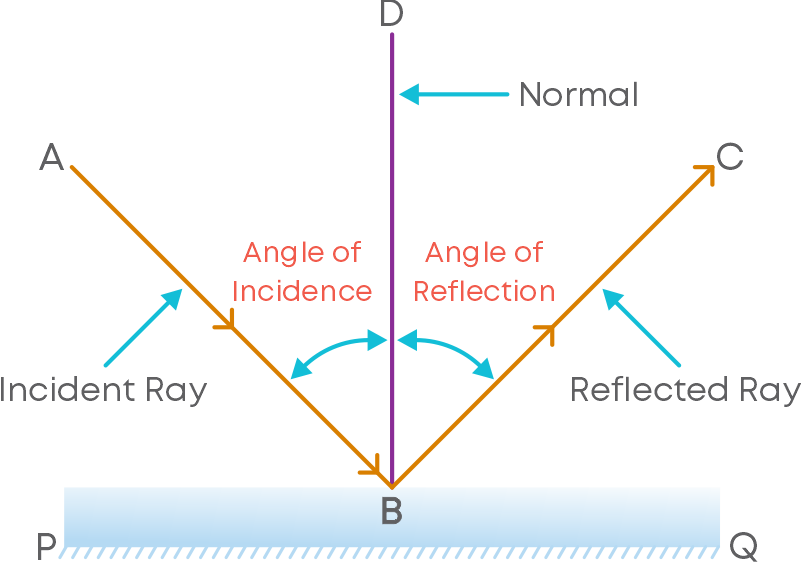
- The normal line DB is the line perpendicular to mirror PQ that divides the angle between the incident ray AB and the reflected ray BC into two equal angles
- The angle between the incident ray and the normal is known as the angle of incidence.
- The angle between the reflected ray and the normal is known as the angle of reflection.
- Angle of incidence = Angle of reflection
∠ABD = ∠DBC
Also, ∠DBP = ∠DBQ = 90⁰
We can apply Linear Pair Axiom to solve various problems. The strategy to apply the theorems and solve is as follows:
- Observe the given figure carefully.
- Identify the angles and the relation between them.
- Apply the appropriate theorem to find the unknown angles.
Vertically Opposite Angles
In the figure given below, rays YW, and the opposite ray YV stand on the line OZ. What does this mean?
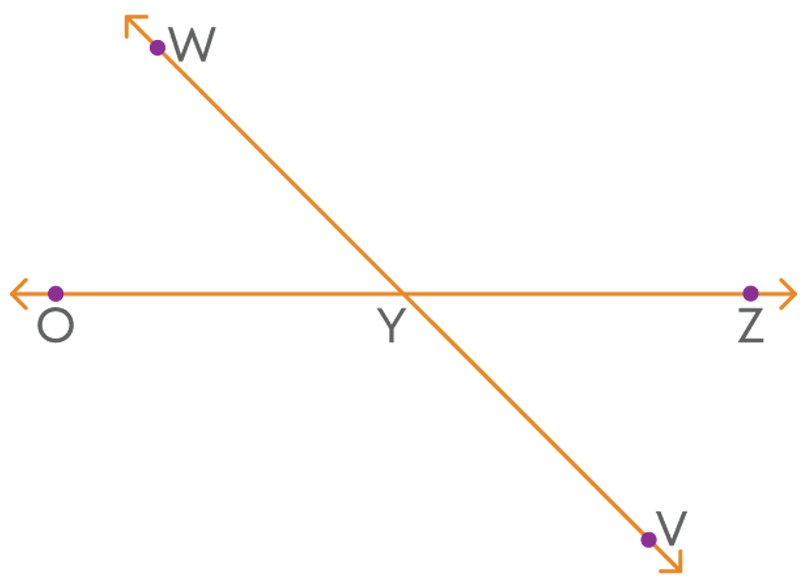
This means that lines OZ and WV are intersecting lines and the vertically opposite angles formed are:
∠WYO and ∠VYZ
∠WYZ and ∠OYV
What can you say about the relation between these angles? Let us see one theorem to know more.
THEOREM
If two lines intersect each other, then the vertically opposite angles are equal.
Consider this: Two lines AB and CD intersect each other at point O.
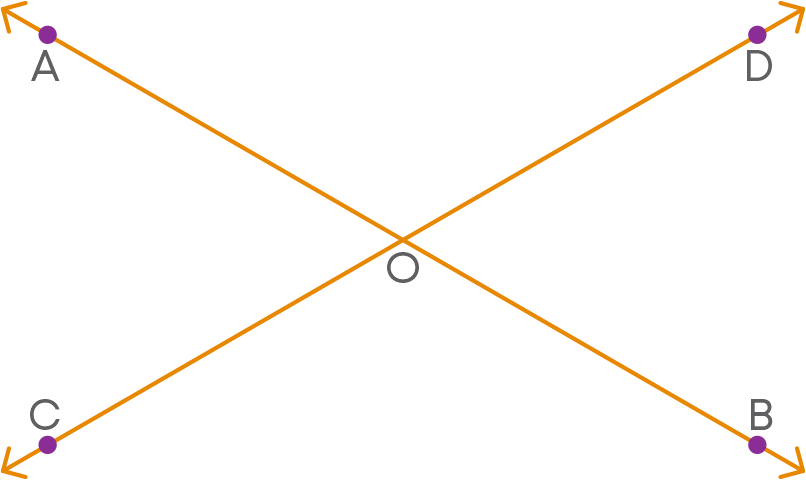
Prove that:
- 1. ∠AOC = ∠BOD
- 2. ∠AOD = ∠BOC
Proof:
Since ray OA stands on the line CD, we have
∠AOC + ∠AOD = 180⁰ ------ (1)
Again, ray OD stands on the line AB, we have
∠AOD + ∠BOD = 180⁰ ------ (2)
From (1) and (2),
∠AOC + ∠AOD = ∠AOD + ∠BOD
∠AOC = ∠BOD
Similarly, ∠AOD = ∠BOC
Hence, ‘Pair of vertically opposite angles are equal when two lines intersect at a point’.
Now let us consider two intersecting lines shown below.

Let us draw the bisectors of the angles AOC and BOD.
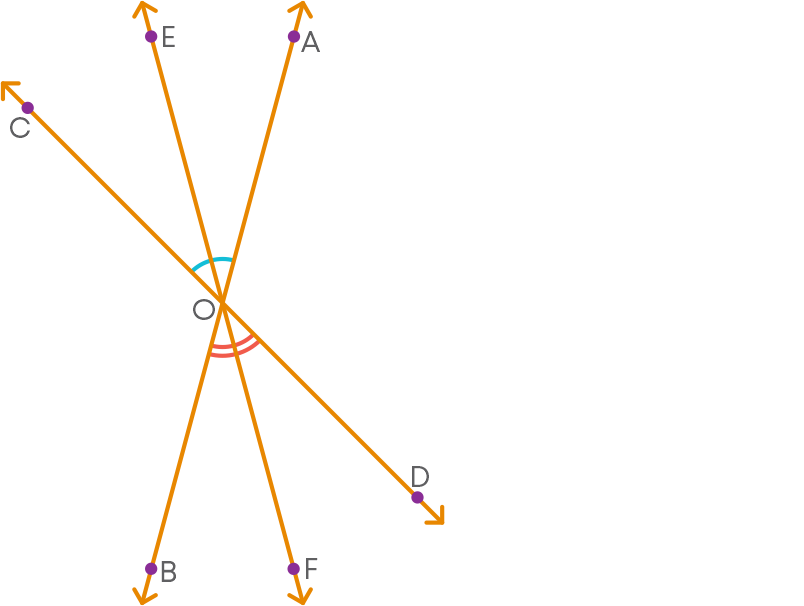
We observe that
- 1. OE and OF are on the same straight line
- 2. The bisectors result in two more pairs of vertically opposite angles
Justification:
Since the sum of all the angles around a point is 360⁰, we have
∠AOC + ∠BOD + ∠COB + ∠AOD
= 360⁰
But ∠COB = ∠AOD as they are vertically opposite angles.
So,
∠AOC + ∠BOD + ∠AOD + ∠AOD
= 360⁰
Also, ∠AOC = 2∠AOE and ∠BOD = 2∠DOF
Since ∠AOC + ∠BOD + ∠AOD + ∠AOD = 360⁰
2∠AOE + 2∠DOF + 2∠AOD = 360⁰
2(∠AOE + ∠DOF + ∠AOD) = 360⁰
∠AOE + ∠DOF + ∠AOD = 180⁰
∠EOF is a straight angle. Hence, EOF is a straight line.
This means that OE and OF are parts of the same straight line.


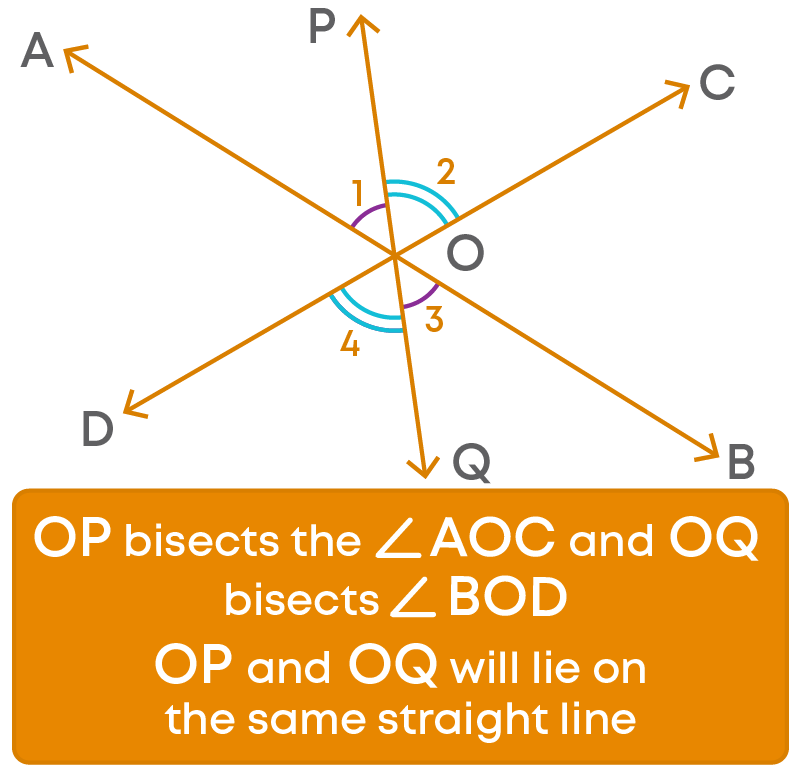
Property of bisectors of vertically opposite angles:
- Bisectors of vertically opposite angles are on the same straight line.
- The bisectors result in two more pairs of vertically opposite angles.

We can solve various problems based on vertically opposite angles using related theorems The strategy to apply the theorems and solve is as follows:
- 1. Observe the given figure carefully.
- 2. Identify the angles and the relation between them.
- 3. Apply the appropriate theorem to find the unknown angles..
Parallel Lines and Transversal
In the figure, 'p' is the transversal to the two parallel lines 'q' and 'r'.
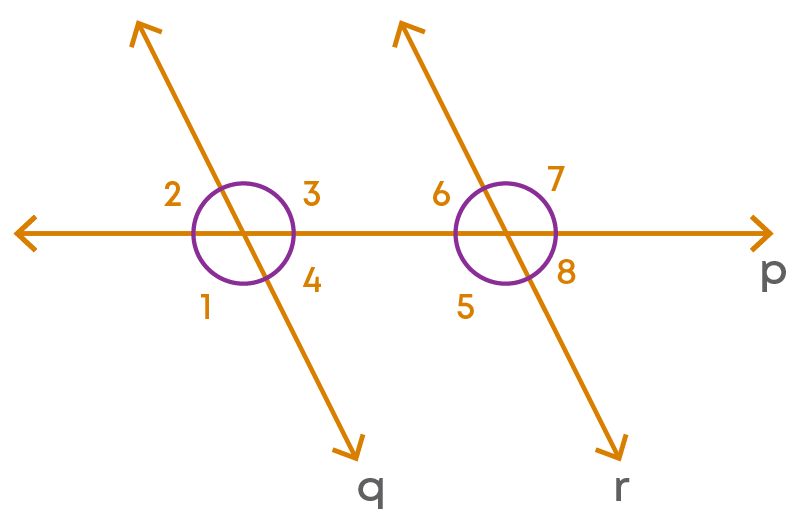
The corresponding angles are:
- ∠1 and ∠5
- ∠4 and ∠8
- ∠2 and ∠6
- ∠3 and ∠7
Now let us cut the line p at a point between the lines 'r' and 'q' and place the line ‘r’ on the line ‘q’.

So, we observe that the following pairs of angles coincide exactly:
- ∠1 and ∠5
- ∠4 and ∠8
- ∠2 and ∠6
- ∠3 and ∠7
So, we can say that each pair of corresponding angles are equal. Hence, if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. This is called corresponding angles axiom.
If a transversal cuts two lines, making a pair of corresponding angles equal, then are the lines parallel? Let us see an example:
Consider the figure.
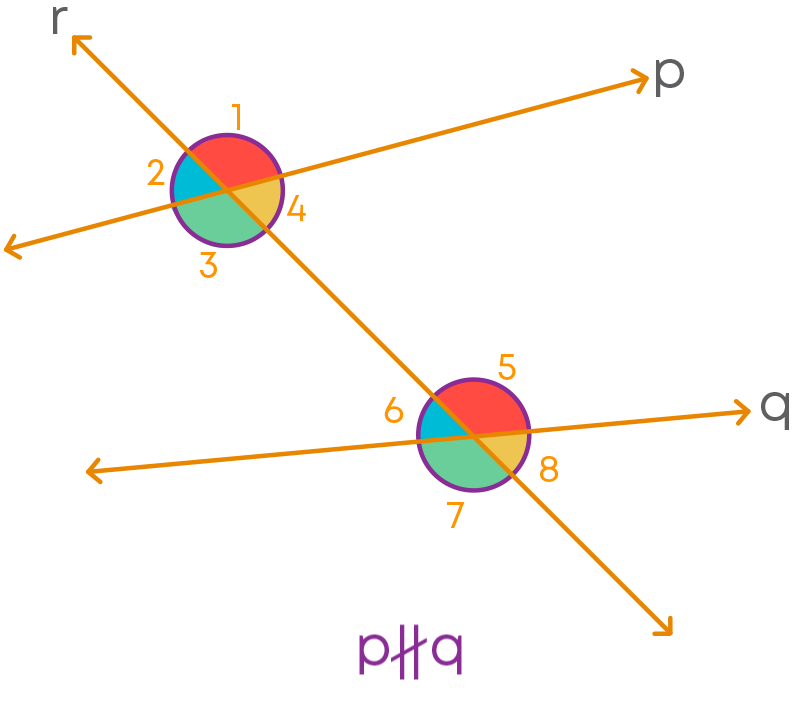
The corresponding angles are:
- ∠2 and ∠6
- ∠3 and ∠7
- ∠1 and ∠5
- ∠4 and ∠8

Clearly these angles are not equal. Also, p ∦ q.
Consider the figure, transversal 'c' cuts two lines 'a' and 'b'.

The corresponding angles are such that:
- ∠2 and ∠6
- ∠3 and ∠7
- ∠1 and ∠5
- ∠4 and ∠8
Hence, a∥b. So, if a transversal cuts two lines, making a pair of corresponding angles equal, then the lines are parallel. This is nothing but the converse of corresponding angles axiom.

Now let us explore the relation between each pair of alternate interior angles when a transversal intersects two parallel lines.
If a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.
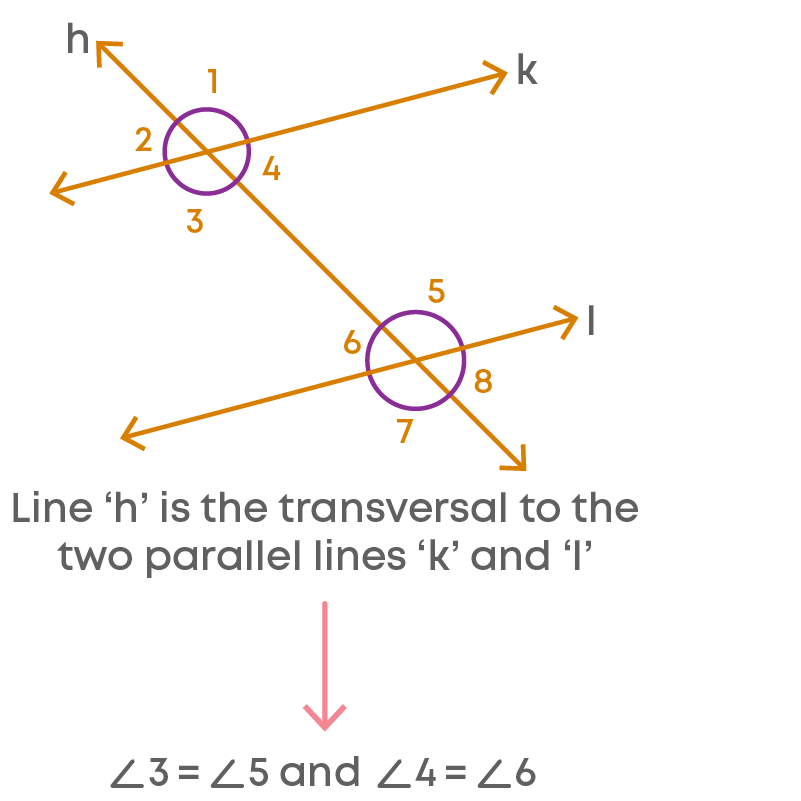

Also, if a transversal intersects in such a way that a pair of alternate interior angles are equal, then the two lines are parallel.
Example: A transversal ‘m’ cuts AB at E and CD at F such that ∠3 = ∠6.
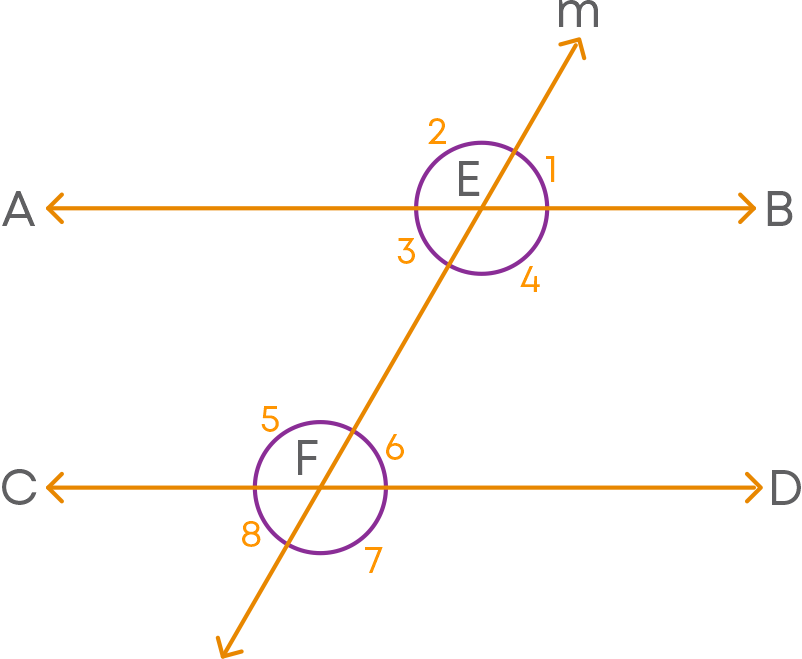
We must prove that AB ∥ CD. We already know that ∠3 = ∠6. Since ∠3 and ∠1 are vertically opposite angles, ∠3 = ∠1. Therefore, ∠1 and ∠6.
But these are corresponding angles. So, by the converse of corresponding angles axiom, AB ∥ CD.
Hence, proved.

Now let us explore the relation between each pair of interior angles on the same side of the transversal intersecting two parallel lines.
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
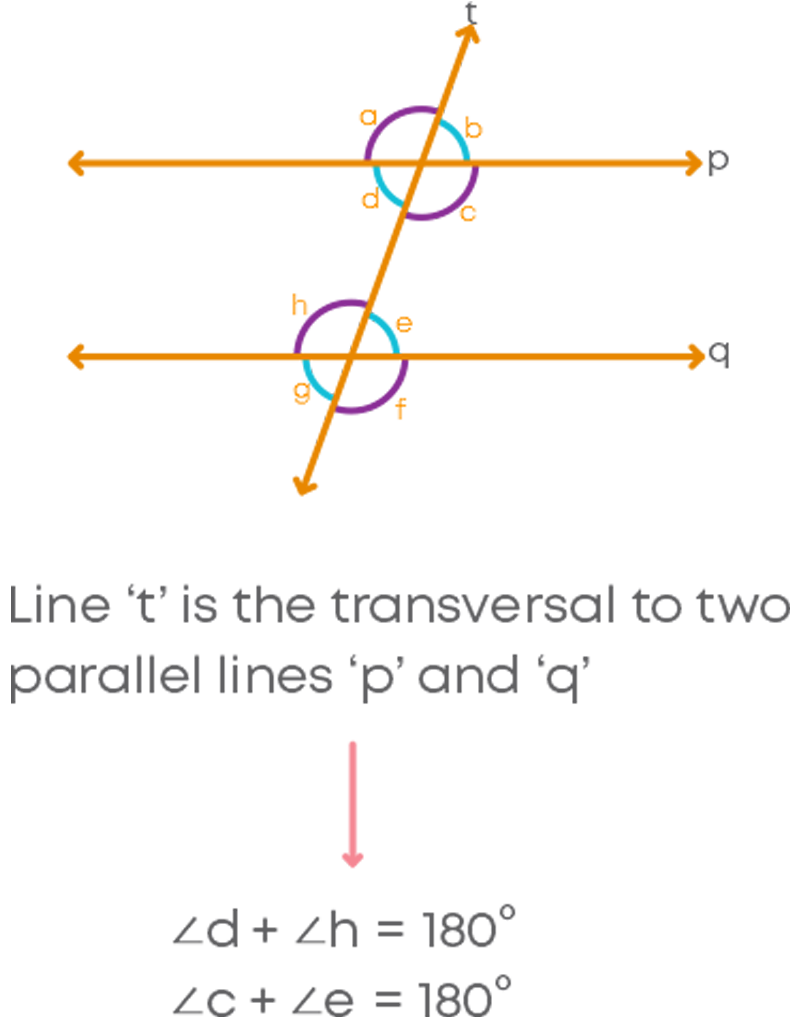
Remember: interior angles on the same side of a transversal are called consecutive interior angles or co-interior angles.
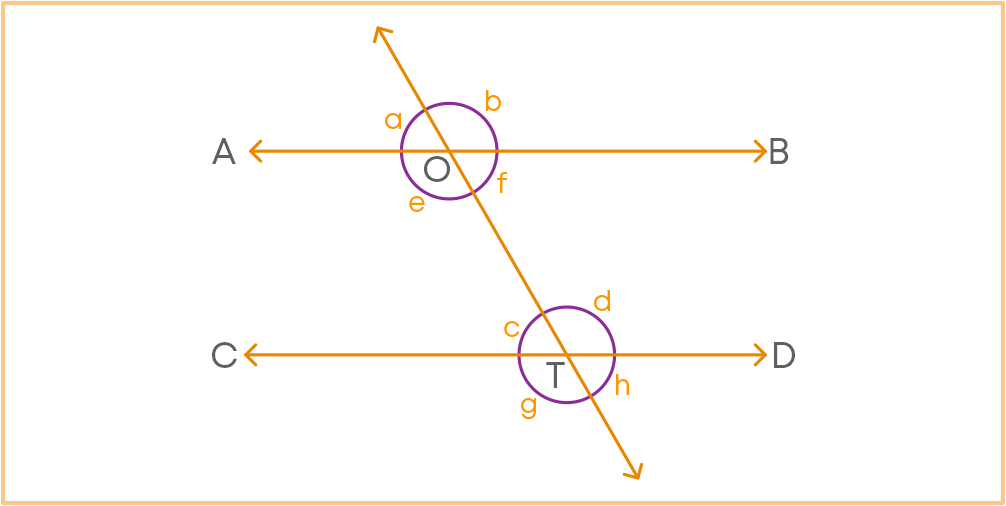
The interior angles that are on the same side of the transversal are ∠e and ∠c, and ∠f and ∠d.
Also:

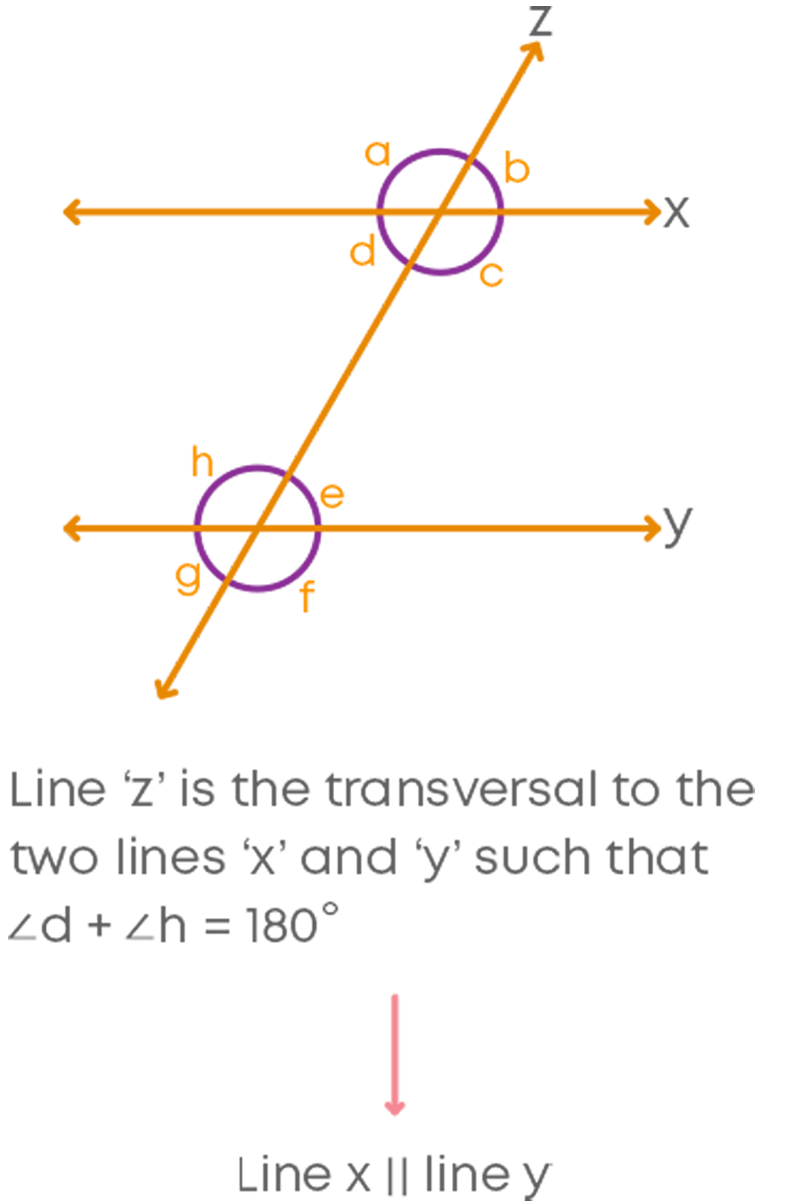
Remember another theorem: Two lines perpendicular to the same line are parallel to each other. Consider:
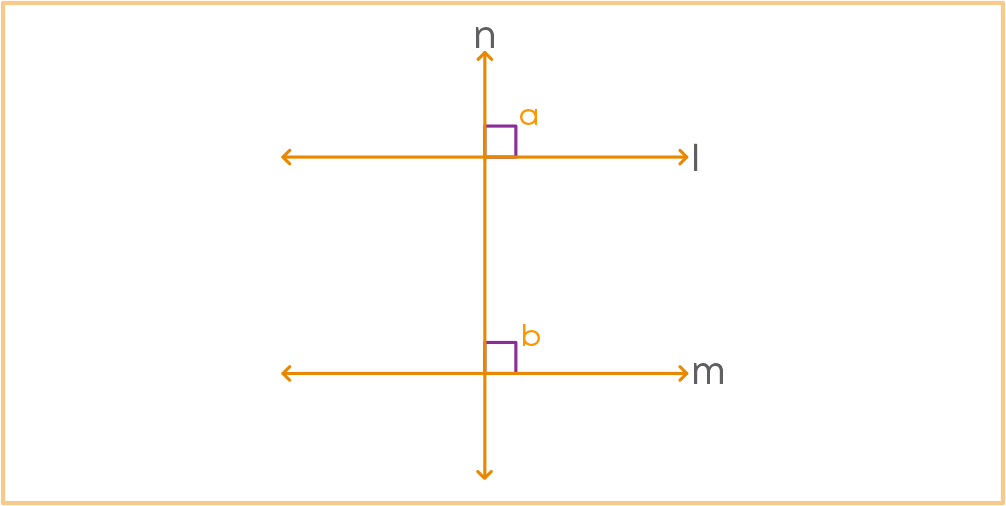
In this figure, l∥m.
Lines Parallel to The Same Line
We see that lines which are parallel to the same line are also parallel.
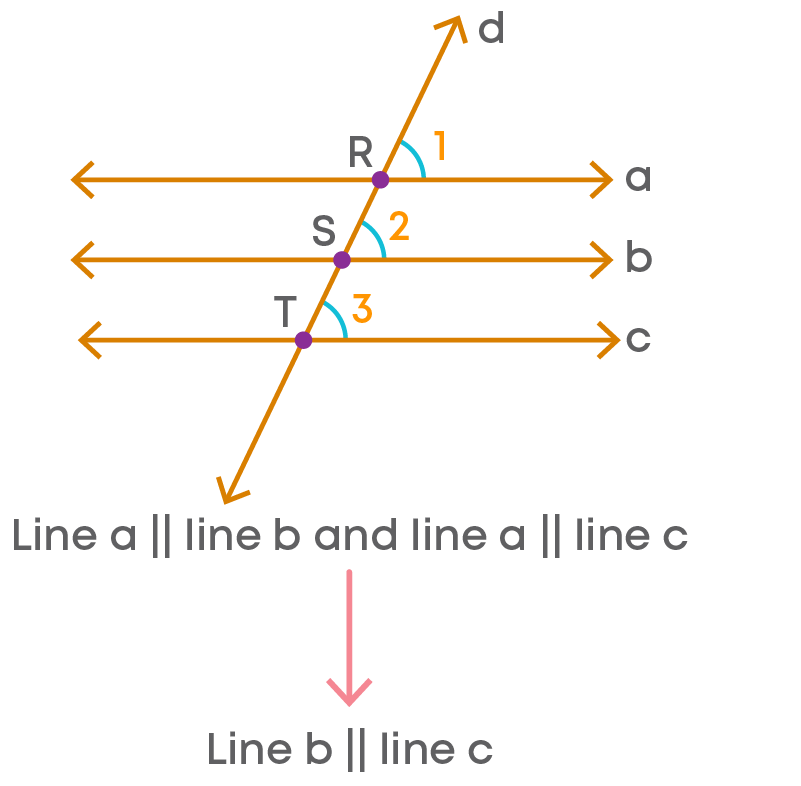
This can be written as a∥b∥c.
This property can be extended to more than two lines.
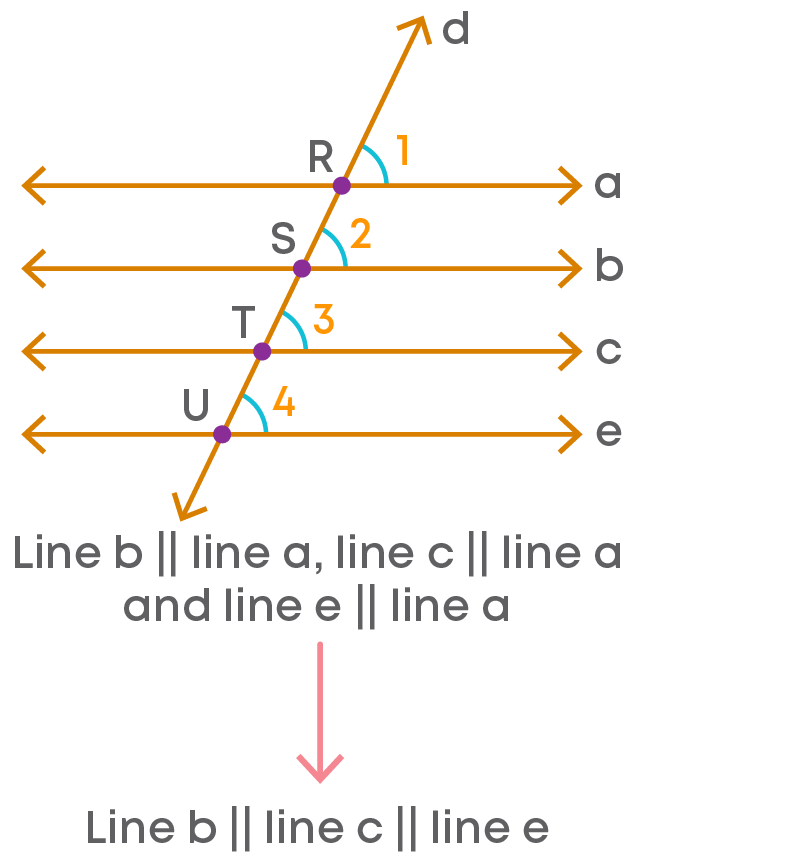
This can be written as a∥b∥c ∥ e.
Angle Properties of a Triangle
We see that the sum of the angles of a triangle is 180⁰.
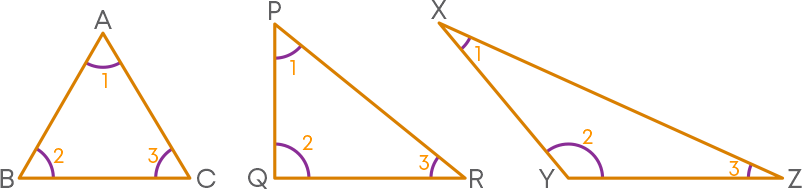
This property is true for all types of triangles. To prove this property, consider:
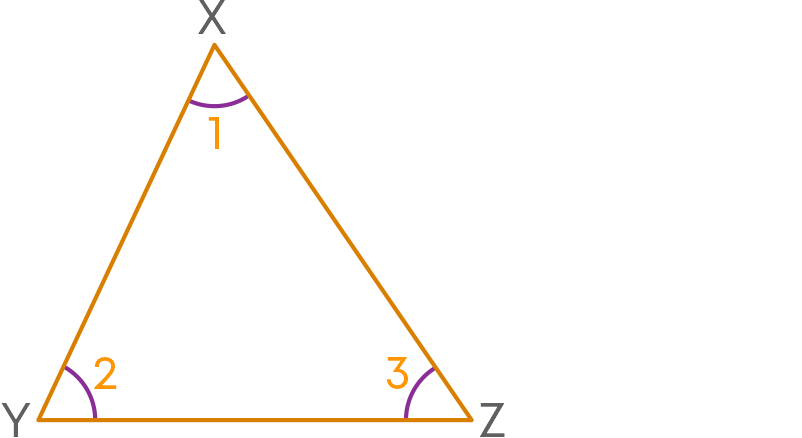
Through vertex X, draw a line PXQ∥YZ.
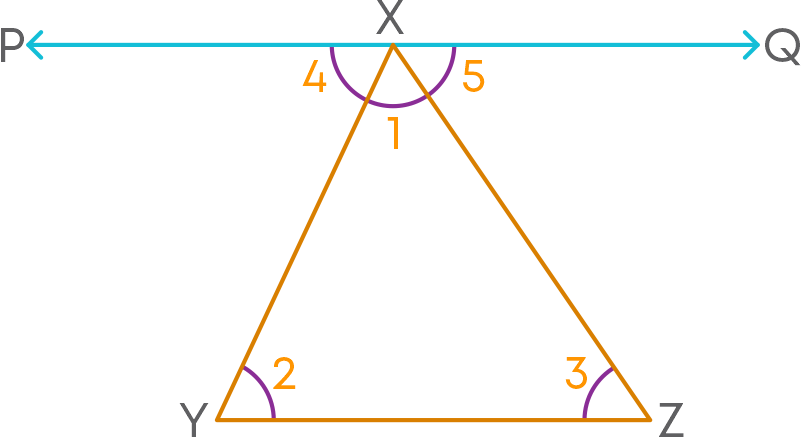
PXQ∥YZ and XY is a transversal.
∠4 = ∠2 -------(i) as they form a pair of alternate interior angles.
PXQ∥YZ and XZ is a transversal.
∠5 = ∠3 -------(ii) as they form a pair of alternate interior angles
Now, ∠4, ∠1, and ∠5 are angles on the same side of line XY, so ∠4 + ∠5 + ∠1 = 180⁰.
Substitute ∠4 = ∠2 and ∠5 = ∠3 from equations (i) and (ii)
∠2 + ∠3 + ∠1 = 180⁰.
Hence, proved.


Consequences of the angle sum property of a triangle:

Now consider triangle ABC.

Now, extend the side BC of triangle ABC.

By extending the side BC, we can see that angle ACD is formed. Does ∠ACD lie on the exterior of triangle ABC? Yes, we can see that ∠ACD lies on the exterior of triangle ABC.
We call this angle as an exterior angle of triangle ABC.
An exterior angle if a triangle is an angle formed by one side of the triangle and the extended side adjacent to this side.
Also, the angle which is adjacent to the exterior angle is known as the interior adjacent angle. For example,
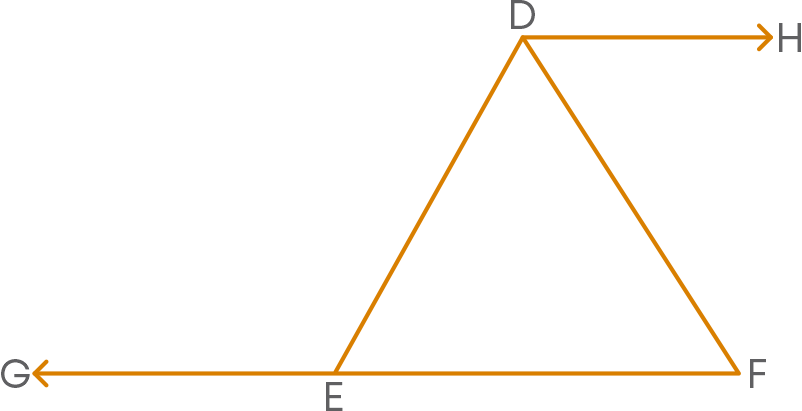
Here we call ∠DEF as an interior adjacent angle. Let us understand what an interior opposite angle in a triangle is.
Consider triangle PQR with ∠PRS as an exterior angle.
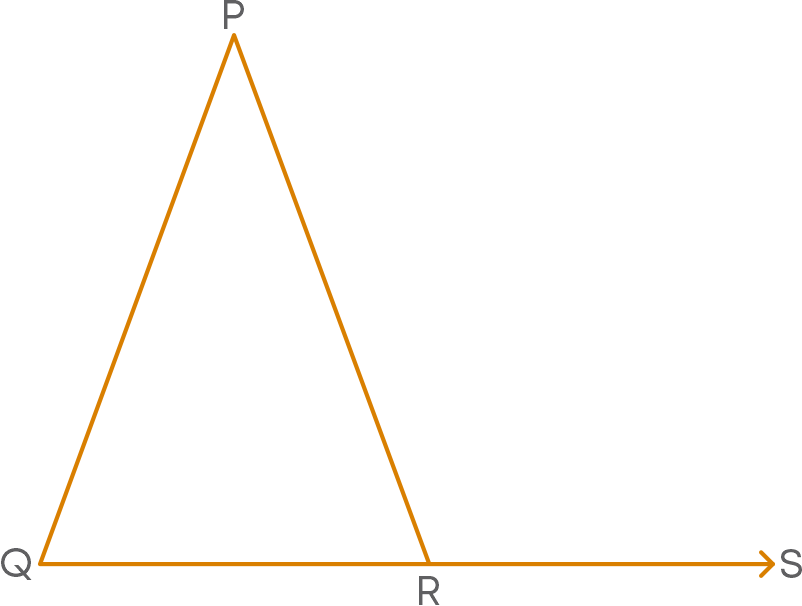
Here ∠PRQ is the interior adjacent angle for the exterior ∠PRS. The remaining two angles inside the triangle namely ∠PQR and ∠QPR are known as interior opposite angles.

Interior opposite angles of an exterior angle of a triangle are the angles other than the interior angle which is adjacent to the exterior angle.
Now, we know about an exterior angle of a triangle and its interior opposite angles; let us see a theorem to see the relation between them.
Theorem: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

Common Errors
The following are topics in which students make common mistakes when dealing with lines and angles:
- 1. Vertically Opposite Angles
- 2. Corresponding Angles
- 3. Co-Interior Angles
- 4. The Exterior Angle Property Of A Triangle
Vertically Opposite Angles
Vertically opposite angles are formed when two lines intersect each other.
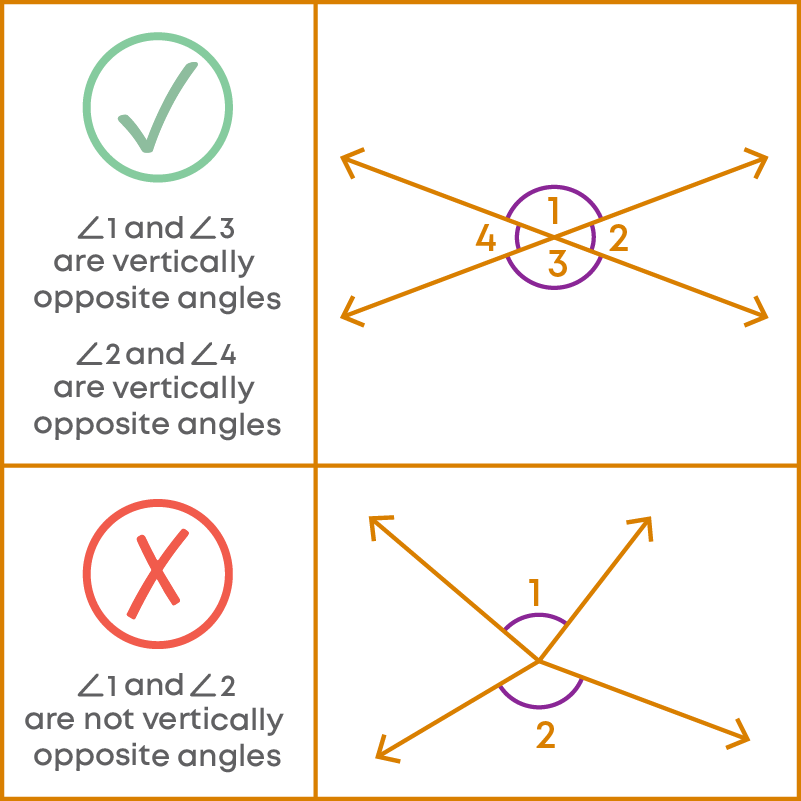
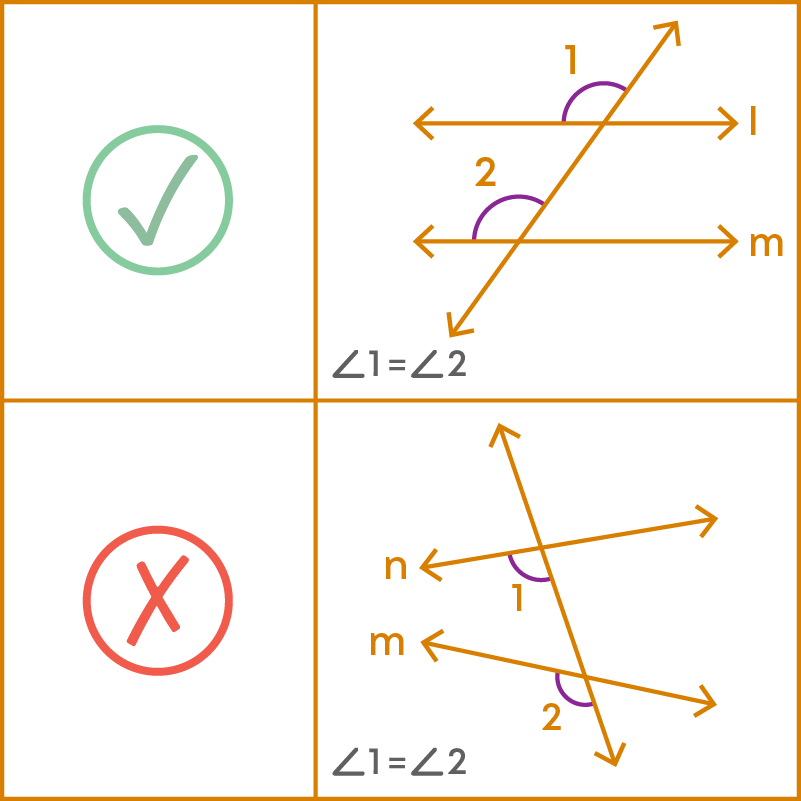
Corresponding Angles
If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
Corresponding angles are equal only when the lines are parallel. The same condition holds good for alternate angles also.
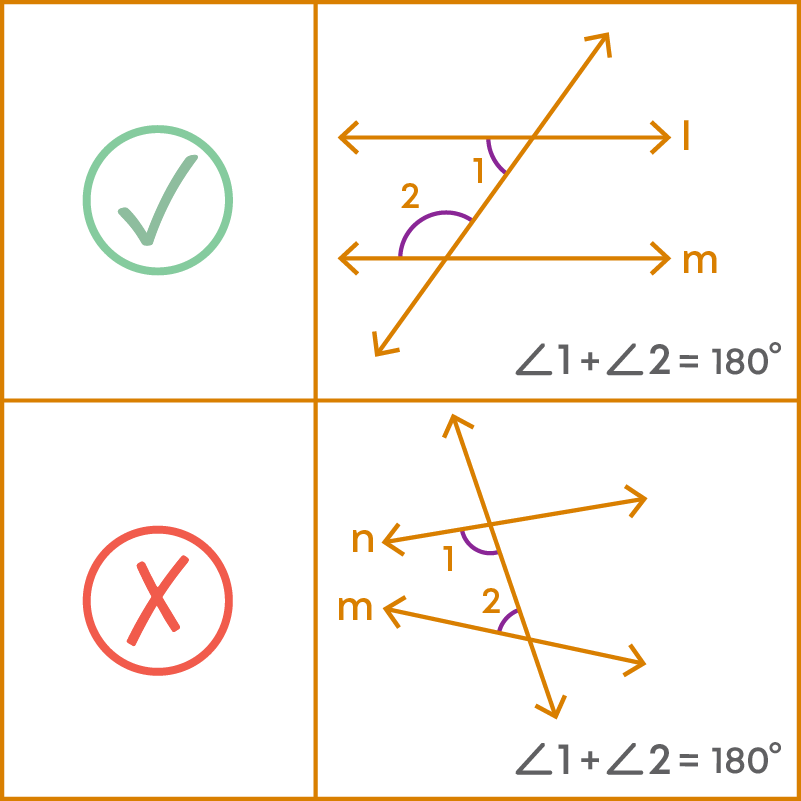
Co-interior Angles
If a transversal intersects two parallel lines, then each pair of co-interior angles are supplementary.
Co-interior angles are supplementary only when the lines are parallel.
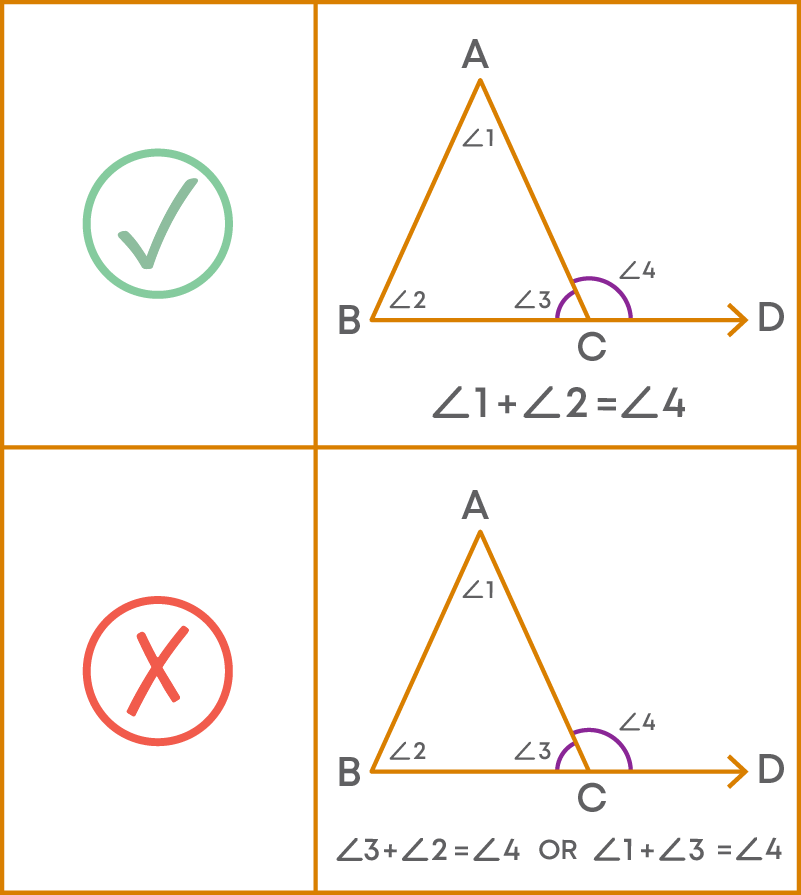
The Exterior Angle Property Of A Triangle
If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
Conclusion
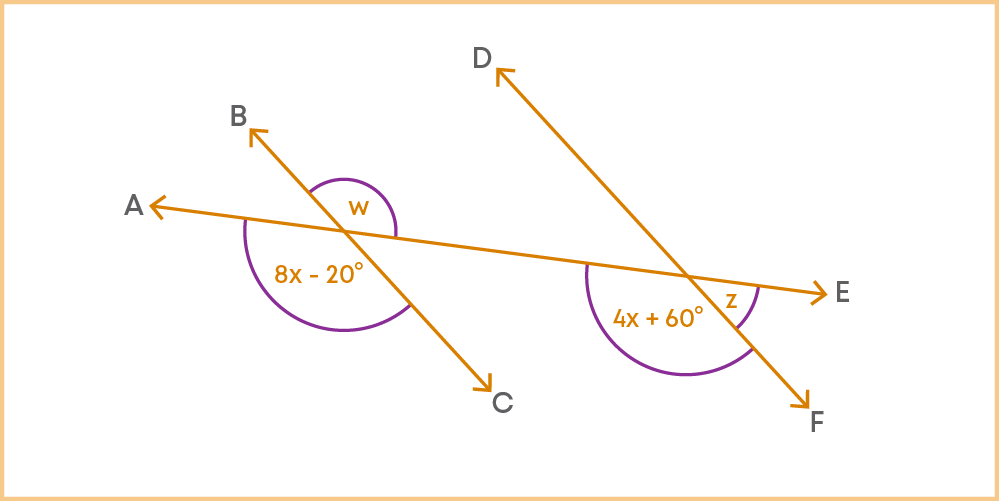
Lines and angles are all around us, hence, it is important to learn about their properties. Can you solve this riddle based on lines and angles?
AE, BC, and DF are straight lines. Janvi assumes that BC and DF are parallel. Help her find angle z: