Introduction
Consider a pack of cards:

Both the cards have the same shape and size. If you take any other card from the pack, will it be of the same shape and size as the cards we took out previously? Yes. Such objects are called congruent objects.
Two figures are said to be congruent if they have the same shape and size. For example, consider these two figures,

- Figure F1 is congruent to figure F2
- This can be represented as F1 ≅ F2
Let us watch the video and understand some real-life examples of congruent figures.
Now you know that there are many applications of congruent figures in real life around us.
Concepts
The chapter ‘Triangles’ covers the following concepts:
Criteria For Congruence of Triangles
You know that the six elements of a triangle are its three sides and three angles. If six elements of one triangle are equal to the corresponding six elements of another triangle, then the two triangles are congruent.
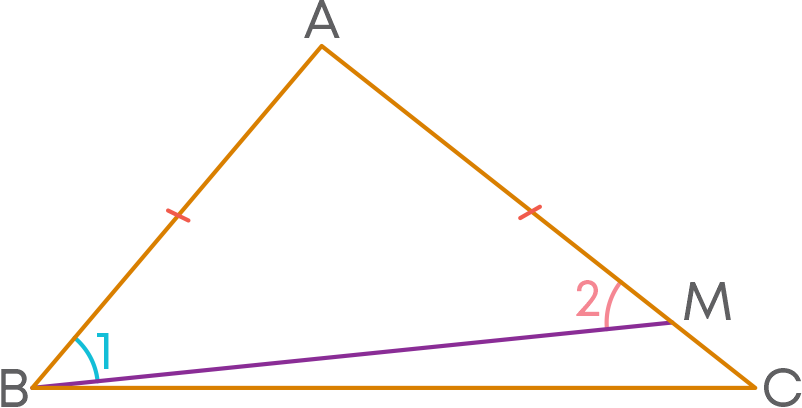
Consider these triangles, ∆MNO and ∆PQR.
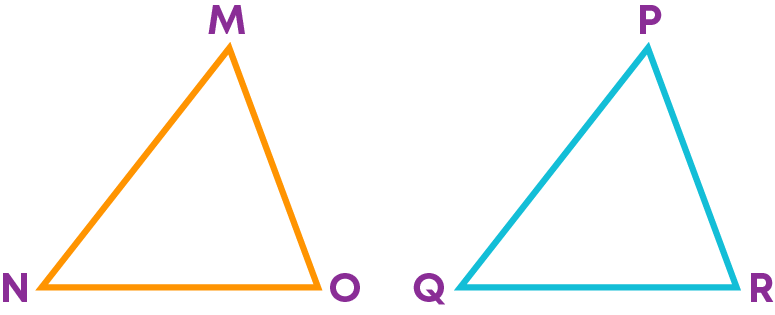
Let us use the method of superposition and check if the triangles are congruent.

The triangles overlap each other exactly on superpose. When we superposed ∆MNO and ∆PQR, the triangles overlapped exactly because:
- ∠P falls on ∠M
- ∠Q falls on ∠N
- ∠R falls on ∠O
- Side PQ falls along Side MN.
- Side PR falls along Side MO.
- Side QR falls along Side NO.
Hence, ∆MNO and ∆PQR are congruent. This can be written as ∆MNO ≅ ∆PQR.
Remember: Arcs are used to show which angles are equal. Slash marks are used to show which sides are equal.
Correspondence is denoted by ‘↔’ and congruence is denoted by ‘≅’.
If a triangle can be translated, rotated, or reflected onto another triangle so that all the vertices correspond, the triangles are congruent triangles. The parts of congruent triangles that ‘match’ are called corresponding parts.
Now, what are the required conditions to check the congruence of two triangles? Let us see!
We have different criteria which help us prove that two triangles are congruent. Each criterion has a different combination of corresponding parts, which should be equal.
The different criteria are as follows:
- Side - Angle - Side (SAS)
- Side - Side - Side (SSS)
- Angle - Side - Angle (ASA)
- Angle - Angle - Side (AAS)
- Right angle – Hypotenuse – Side (RHS)
In two triangles, if one of these conditions satisfy, then the given triangles are congruent.
SAS Congruence
If two sides and the included angle of a triangle are equal to two corresponding sides and the included angle of another triangle, then the triangles are congruent. Let us prove this.
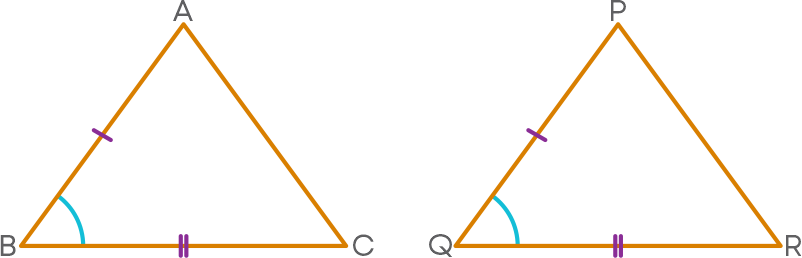
Consider the ∆ABC and ∆PQR.
It is given that ∠B = ∠Q, AB = PQ, and BC = QR. Let us superpose ∆ABC and ∆PQR such that ∠B falls on ∠Q, side AB falls along PQ, and side BC falls along QR.

When we superimposed ∆ABC and ∆PQR, the triangles overlapped exactly because:
- ∠A falls on ∠P
- ∠Q falls on ∠B
- ∠C falls on ∠R
- Side AB falls along side PQ
- Side BC falls along side QR
- Side CA falls along side RP
In ∆ABC and ∆PQR,
∠A = ∠P (by superimposition)
∠B = ∠Q (given)
∠C = ∠R (by superimposition)
AB = PQ (given)
BC = QR (given)
CA = RP (by superimposition)
Hence, ∆ABC and ∆PQR are congruent, or ∆ABC ≅ ∆PQR.
If two sides and the included angle of a triangle are equal to two corresponding sides and the included angle of another triangle, then the triangles are congruent. This is the Side-Angle-Side criterion or SAS congruence criterion.
Remember, for two triangles to be congruent, two pair of corresponding sides and the included angles must be equal.
From the SAS congruence criterion, we get the following theorem:
Theorem: Angles opposite to equal sides of an isosceles triangle are equal.

Here ∠B = ∠C.
Theorem: If the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles.
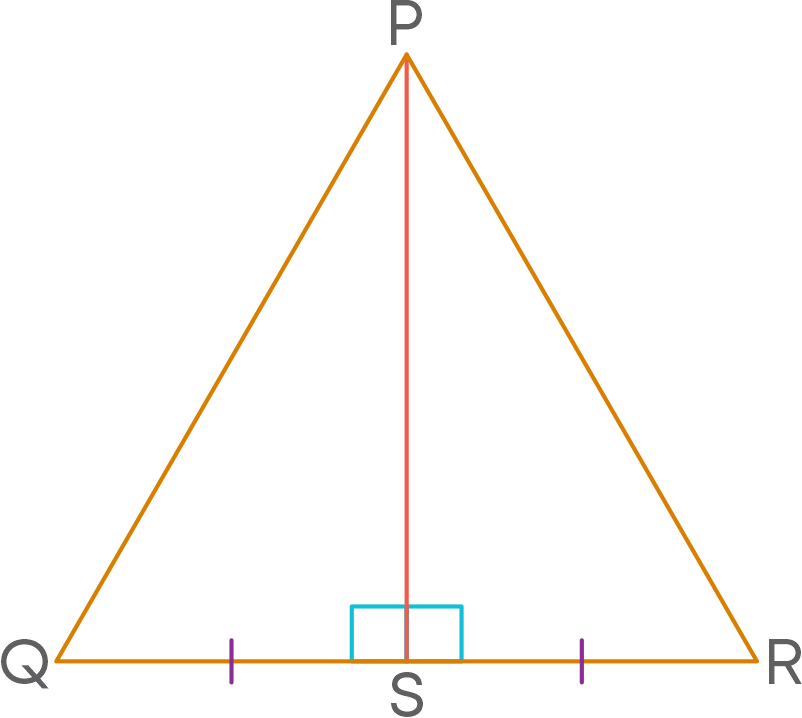
Here we can prove that ∆PQS ≅ ∆PRS using SAS congruence criterion. Therefore, we can say that PQ = PR (CPCT). Hence, triangle PQR is an isosceles triangle.
To solve problems based on SAS congruence criterion,
- Analyse the question by identifying what is given and what we are asked to find or prove.
- Identify the triangles which we must prove are congruent.
- In the given set of triangles, identify the corresponding parts which are equal.
- Check if the SAS congruence can be applied to prove that the given set of triangles are congruent.
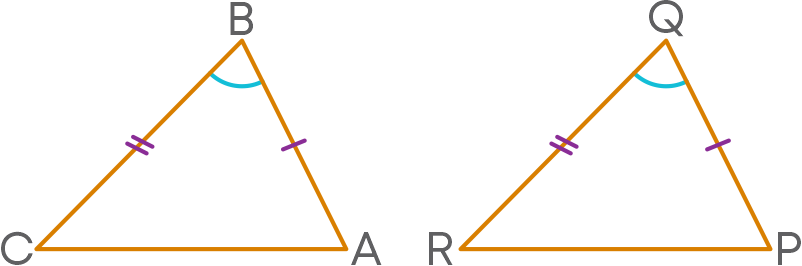
SSS Congruence
If under a given correspondence, the three sides of one triangle are equal to the three corresponding sides of another triangle, then the triangles are congruent. This is known as side-side-side or SSS congruence.
How do we prove this? Consider:
It is given that AB = PQ, BC = QR, and AC = PR.
Suppose BC is the longest side. Draw QS such that ∠RQS = ∠ABC and QS = AB. Join R and S.
In ∆ABC and ∆SQR,
BC = QR (given)
∠RQS = ∠ABC (by construction)
QS = AB (by construction)
Therefore, by SAS congruence criteria, ∆ABC ≅ ∆SQR.
∠A = ∠G and AC = SR
Now, AB = QS and AB = PQ.
Hence, PQ = QS ---- (1)
Similarly,
AC = PR and AC = SR
Hence, PR = SR ---- (2)
In ∆PSR, PR = SR (from 2)
∠RPS = ∠SRP (Angles opposite to equal sides of a triangle are equal) ------ (3)
In ∆PSQ, PQ = QS (from 1)
∠QPS = ∠QSP (Angles opposite to equal sides of a triangle are equal) ------ (4)
From 3 and 4,
∠RPS + ∠QPS = ∠SRP + ∠QSP
∠P = ∠S
∠S = ∠A (proved above)
So ∠P = ∠A ----- (5)
Thus, in ∆ABC and ∆PQR,
AB = PQ (given)
∠P = ∠A (from 5)
AC = PR (given)
Therefore, by SAS congruence criteria we obtain, ∆ABC ≅ ∆PQR.
ASA Congruence
If under some correspondence, two angles and the included side of a triangle are equal to two corresponding angles and included side of another triangle, then the triangles are congruent.
Let us consider two triangles ABC and PQR such that ∠A = ∠P, ∠B = ∠Q, and BC = QR.
We need to prove that ∆ABC ≅ ∆PQR. To prove the congruence of the two triangles, three cases arise.
Case (i) Let AB = PQ
In this case we have, AB = PQ
∠B = ∠Q (given)
And BC = QR (given)
So, by SAS criteria of congruence, we obtain ∆ABC ≅ ∆PQR.
Case (ii) When AB is less than PQ
In this case, take a point M such that AB = MQ. Join MR.
Now in ∆ABC and ∆MQR, we have
AB = MQ (by supposition)
∠B = ∠Q (given)
And BC = QR (given)
So, by SAS criteria of congruence, we obtain ∆ABC ≅ ∆MQR.
∠C = ∠MRQ (cpct)
But ∠C = ∠PRQ (given)
This is possible when ray MR coincides with PR or M coincides with P. Therefore, AB must equal to PQ. Thus, in ∆ABC and ∆PQR, we have
AB = PQ (as proven above)
∠B = ∠Q (given)
And BC = QR (given)
So, by SAS criterion of congruent, we obtain, ∆ABC ≅ ∆PQR.
Case (iii) When AB is greater than PR
In this case, take a point M on PQ produced such that AB = MQ
Now, proceeding exactly on the same lines as in case (ii), we can prove that,
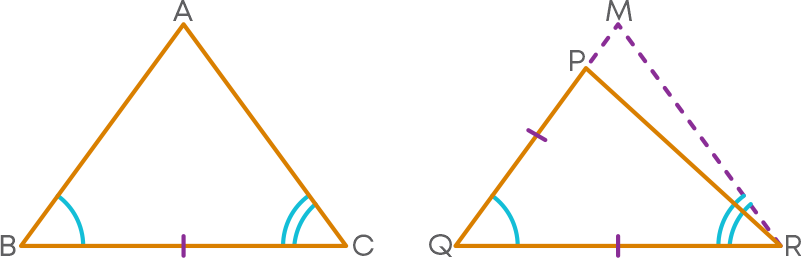
∆ABC ≅ ∆PQR
Hence, in all three cases we obtain ∆ABC ≅ ∆PQR.
Also, angles opposite to equal sides of an isosceles triangle are equal. For example,
ABC is an isosceles triangle in which AB = AC.
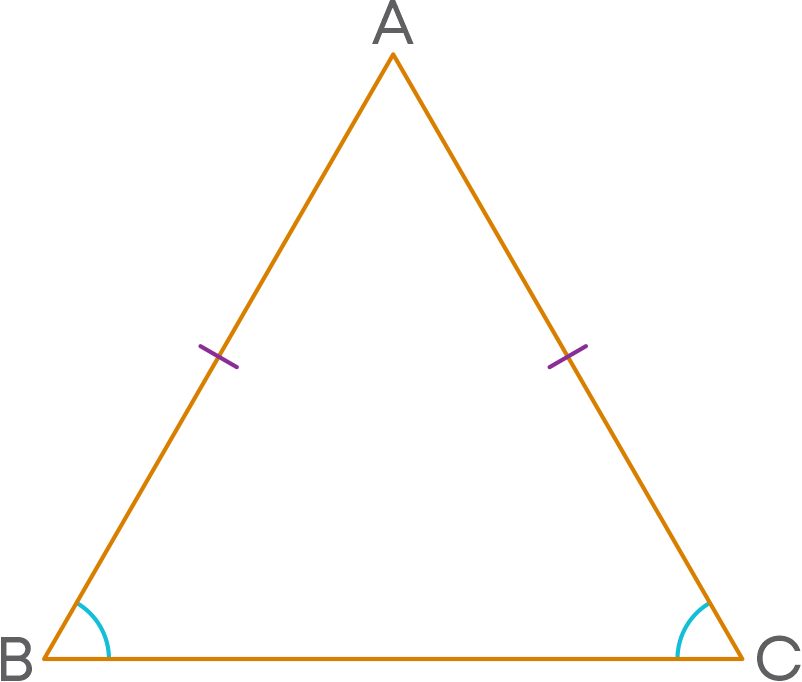
The angle opposite to AB is ∠C and the angle opposite to AC is ∠B.
Hence, ∠B = ∠C.
AAS Congruence
If under some correspondence, two angles and non-included side of one triangle are equal to the corresponding angles and side of the other triangle then the triangles are congruent. Example:
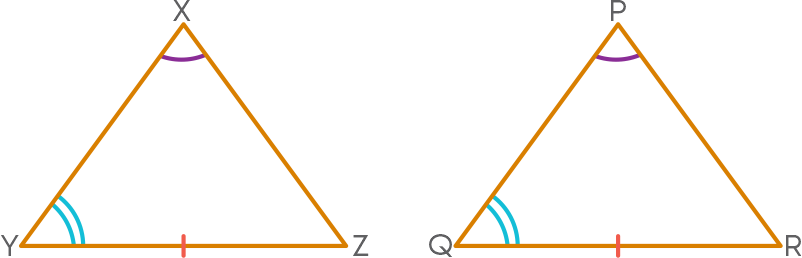
It is given that ∠X = ∠P, ∠Y = ∠Q, and YZ = QR. To prove that ∆XYZ ≅ ∆PQR:
We know that ∠X = ∠P, ∠Y = ∠Q
∠X + ∠Y = ∠P + ∠Q
180⁰ - ∠Z = 180⁰ - ∠R
∠Z = ∠R ------- (1)
Thus, in ∆XYZ and ∆PQR we have,
∠Y = ∠Q (given)
YZ = QR (given)
∠Z = ∠R (from 1)
Hence, by ASA congruence rule, we obtain, ∆XYZ ≅ ∆PQR.
Hence, if two angles and non-included side of one triangle are equal to the corresponding angles and side of the other triangle, then the two triangles are congruent.
For example, in ∆XYZ and ∆PQR,

∠X = ∠P
∠Y = ∠Q
YZ = QR
Hence, ∆XYZ ≅ ∆PQR by AAS congruence criterion.
Remember these points:
- The sides opposite to equal angles of a triangle are equal.
- In an isosceles triangle, the altitude from the vertex bisects the base.
RHS Congruence
If under the correspondence, the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle, then the triangles are congruent.
How do we prove this? Consider:
Two right angles triangles ABC and DEF in which ∠B = ∠E = 90⁰, and AC = DF, BC = EF.
To prove that ∆ABC ≅ ∆DEF:
Construct:
Produce DE to G so that, EG = AB. Join G and F.
In ∆ABC and ∆GEF,
AB = GE (by construction)
∠B = ∠FEG = 90⁰ (∠DEF = 90⁰ and ∠DEF and ∠FEG are linear pair of angles)
BC = EF (given)
So, by SAS congruence of criterion we obtain ∆ABC ≅ ∆GEF
∠A = ∠G (CPCT) ----- (1)
AC = GF (CPCT) ------- (2)
Now AC = GF (from 2)
AC = DF (given)
So, DF = GF
∠D = ∠G (Angles opposite to equal sides in a triangle (∆DGF) are equal) ------(3)
From 1 and 3 we get, ∠A = ∠D ------- (4)
Thus in ∆ABC and ∆DEF, we have
∠A = ∠D (from 4)
∠B = ∠E (given)
∠A + ∠B = ∠D + ∠E
180⁰ - ∠C = 180⁰ - ∠F
∠C = ∠F ---- (5)
Now, in ∆ABC and ∆DEF, we have
BC = EF (given)
∠C = ∠F (from 5)
AC = DF (given)
So, by SAS congruence of criterion we obtain ∆ABC ≅ ∆DEF.
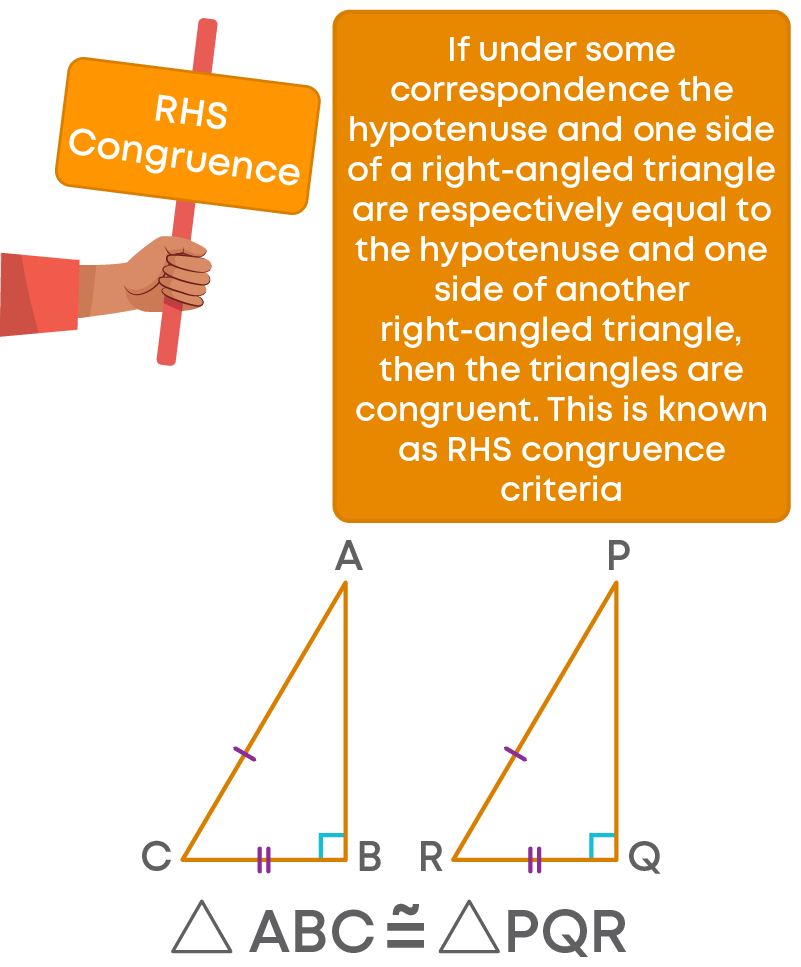
∠B = ∠Q = 90⁰
Hypotenuse AC = PR
Side BC = QR
Hence, ∆ABC ≅ ∆PQR.
Inequalities In A Triangle
In general, if two sides of a triangle are unequal then the angle opposite to the longer side is larger or greater. How do we prove this?
Theorem: If two sides of a triangle are unequal then the angle opposite to the longer side is greater.
Let us represent the given theorem in a figure.
We see that AC > AB. We must prove that ∠ABC > ∠BCA, i.e., ∠B > ∠C.
Now, mark the point M on AC such that AM = AB. Join B and M.
We know that in a triangle, the angles opposite to the equal sides are equal. So, in ∆ABM, AB = AM.
Hence, ∠1 = ∠2 --------- (1)
Now consider the ∆BCM. We find that ∠BMA is the exterior angle of ∆BMC. We know that, an exterior angle is always greater than the interior opposite angle.
∠2 > ∠MCB
∠2 > ∠ACB (since ∠ACB = ∠MCB) --------- (2)
From 1 and 2, we have
∠1 = ∠2 and ∠2 > ∠ACB
∠1 > ∠ACB --------- (3)
But ∠1 is part of ∠ABC. Therefore, ∠ABC > ∠1 --------- (4)
From 3 and 4, we get,
∠ABC > ∠ACB
That is, ∠B > ∠C
Hence, if two sides of a triangle are unequal then the angle opposite to the longer side is greater.
Remember,


Now, let us prove another theorem.
Theorem: In any triangle, the side opposite to the greatest angle is the longest.
We must prove that AC > AB, given that ∠B > ∠C.
In ∆ABC, we have three possibilities.
- 1) AC = AB
- 2) AC < AB
- 3) AC > AB
∠B = ∠C (Angle opposite to equal sides are equal)
But it is given that ∠B > ∠C
Hence, AC ≠ AB
CASE 2: When AC < AB
∠B < ∠C (Angle opposite to longest side is greater)
This also contradicts the given condition ∠B > ∠C. Hence, AC cannot be longer than AB.
CASE 2: When AC > AB
∠B > ∠C (Angle opposite to longest side is greater)
Hence, this case is true.
Theorem: the sum of the lengths of the two sides of a triangle is greater than the third side.
To prove this consider:
We must prove that AB + AC > BC, AB + BC > AC, and BC + AC > AB.
To do this:
Produce side BA to M such that AM = AC. Join CM.
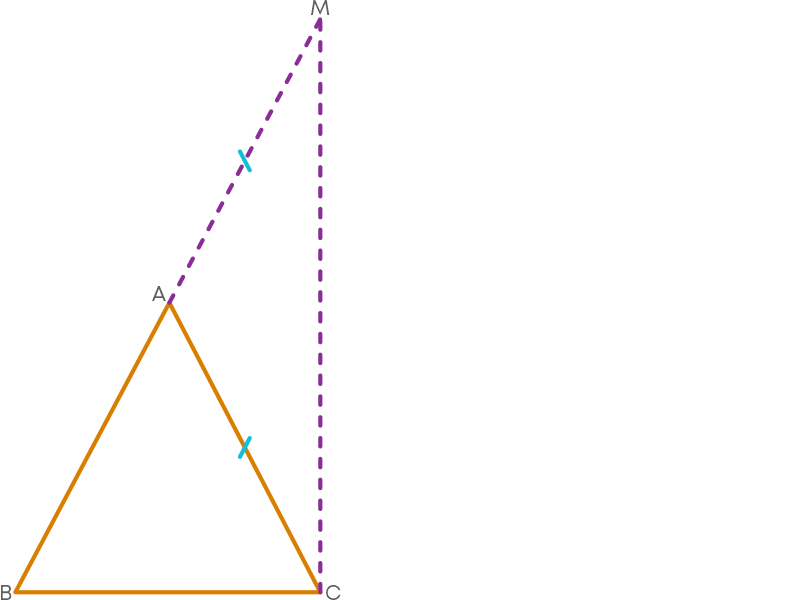
Now, ∠AMC = ∠ACM (Angles opposite to equal sides of a triangle are equal)
So, ∠ACM = ∠AMC
∠ACB + ∠ACM > ∠AMC
∠BCM > ∠AMC (Since ∠ACB + ∠ACM = ∠BCM)
∠BCM > ∠BMC (since ∠AMC = ∠BMC)
BM > BC (Sides opposite to greater angle is larger)
BA + AM > BC
BA + AC > BC (By construction AM = AC)
AB + AC > BC
Hence, AB + AC > BC
Similarly, AB + BC > AC and BC + AC > AB.
If a set of three lengths are given, then the sum of the two lengths should be greater than the third length. Only then can the lengths form a triangle, otherwise the lengths cannot form a triangle.
To solve problems based on the theorems of inequality in a triangle:
- Analyse the question by identifying what is given and what we are asked to find or proof.
- Identify the angles, sides, and the relation between them.
- Apply the appropriate theorem of inequality in a triangle and prove the required.
Common Errors
The following are topics in which students make common mistakes when dealing with triangles:
- 1. AAA congruence
- 2. Importance of included angles in SAS congruence criterion
- 3. Symbolic representation of congruence
- 4. To prove two right angled triangles congruent, using only RHS and ignoring the other congruence
AAA Congruence
There are 2 triangles, ∆ABC and ∆PQR.
∠A = ∠P = 80⁰
∠B = ∠Q = 60⁰
∠C = ∠R = 40⁰
Can you say that ∆ABC ≅ ∆PQR by AAA congruence criterion? No!
Even though the triangles have corresponding angles of the same measure, their sides need not be the same. Hence, they need not be congruent.
Importance Of Included Angles In SAS Congruence Criterion
Consider 2 triangles, ∆ABC and ∆PQR.
∠A = ∠P
AB = PQ
BC = QR
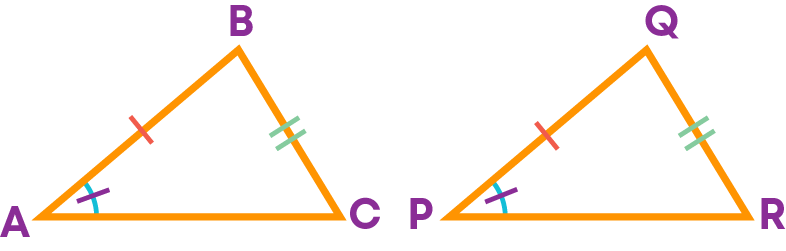
Can you say that the given triangles are congruent? No! We cannot conclude that the given triangles are congruent since equal angles are not included.
Hence, while proving that two triangles are congruent using the SAS congruence criterion, make sure that the angle is included between the sides.
Symbolic Representation Of Congruence
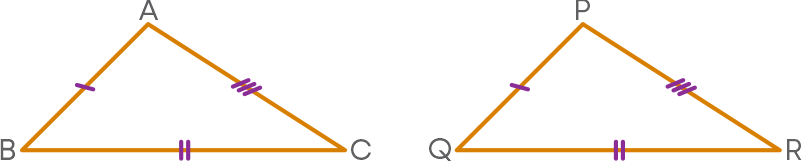
You know that the two triangles ABC and PQR, shown below are congruent by the SSS congruence criterion.
To represent their congruence relation symbolically, you should know the corresponding vertices. From the given figure, it is clear that,
- A <--> Q
- B <--> P
- C <--> R
Hence, ∆ABC ≅ ∆PQR

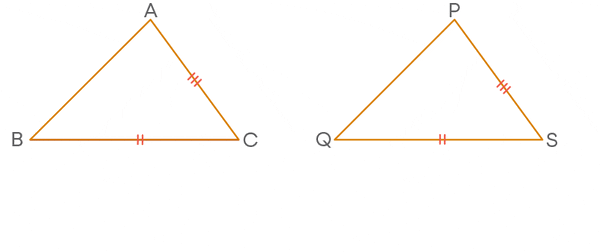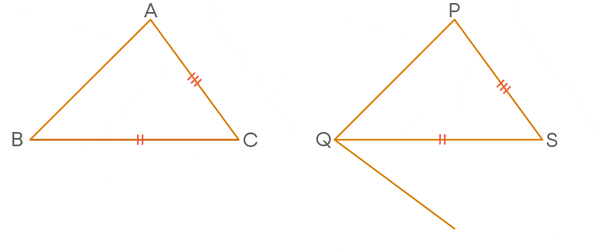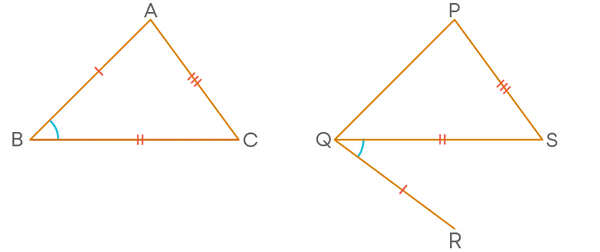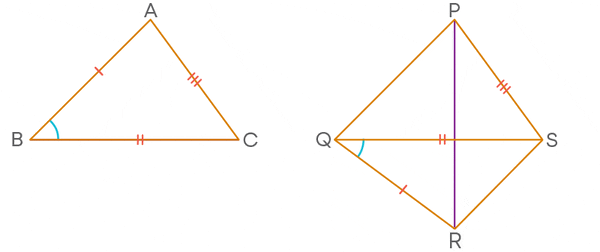
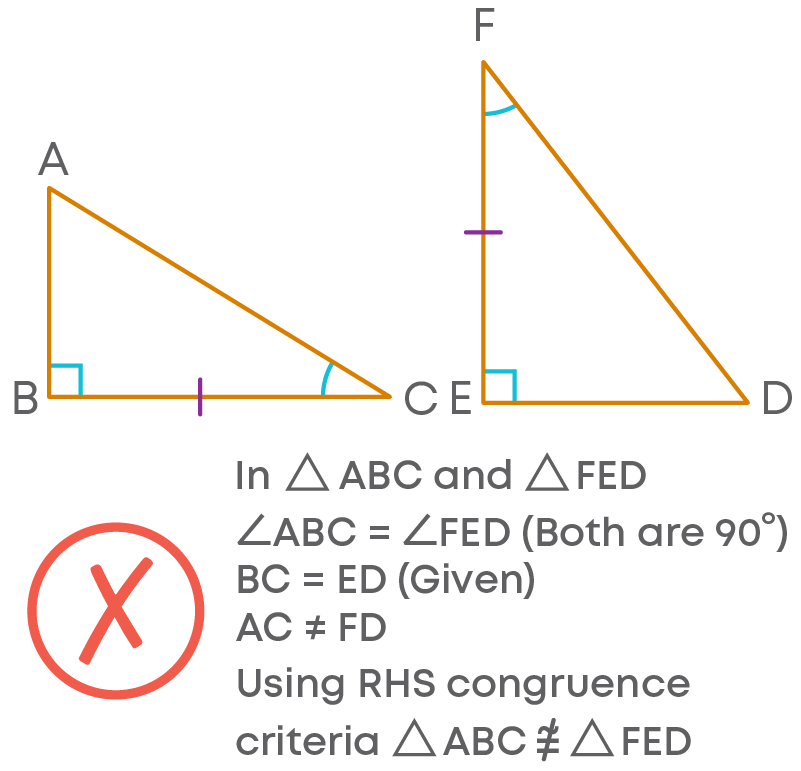
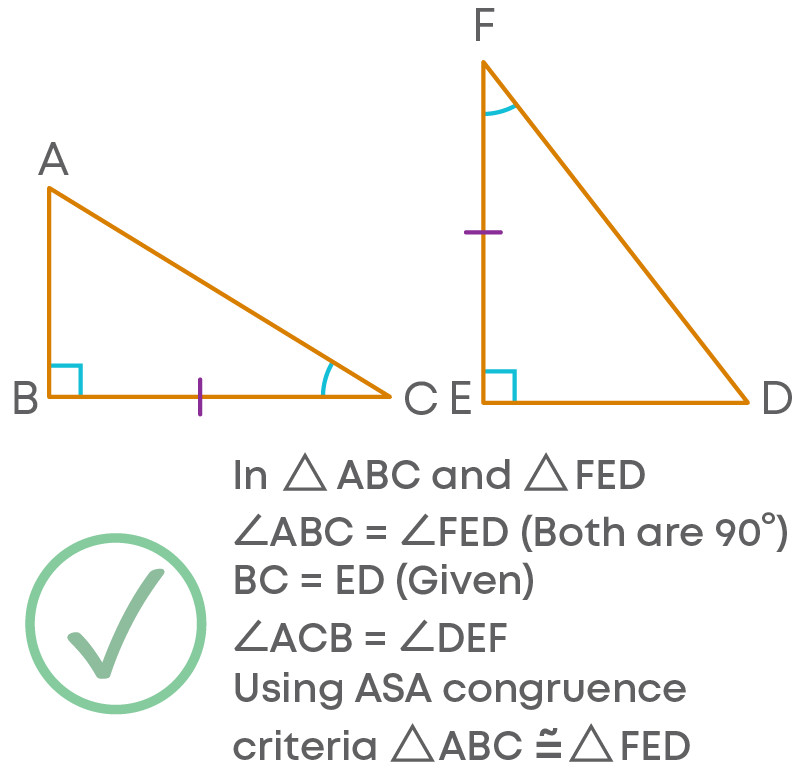
To Prove Two Right Angled Triangles Congruent, Using Only RHS And Ignoring The Other Congruence
In the select congruence criterion, you may make these mistakes. Let us look at an example:
To prove that ∆ABC and ∆FED are congruent. Can we use RHS congruence? No. Here we can use ASA congruence criteria.
Conclusion
By now you have learnt about triangles and other geometric shapes being all around us, but did you know certain properties of triangles can also be found in our daily lives?
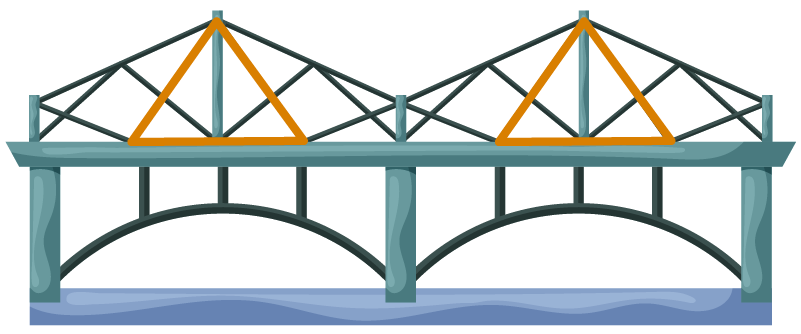
- Congruent triangles are used in constructions which helps structures to have a strong reinforced foundation and remain stable. Due to this property, the structure will not bend or buckle under load or during strong winds. A common sight of congruent triangles is in the construction of bridges.
- In the images below you can see the different criteria of congruence of a triangle being demonstrated through real-world examples:
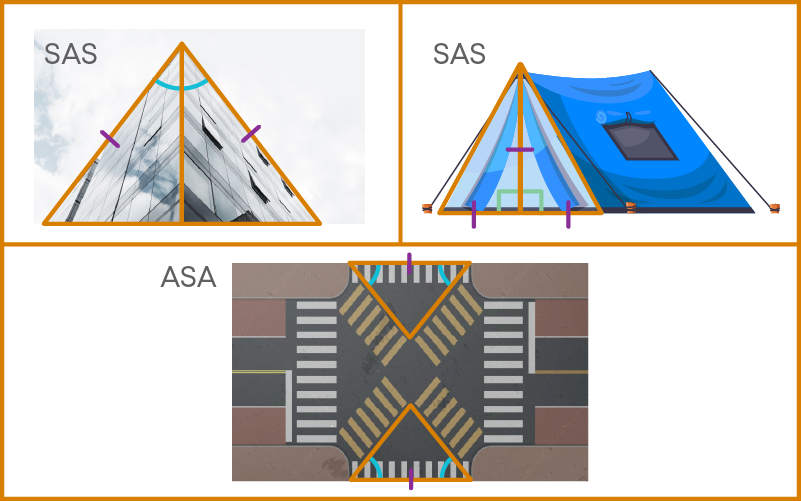
SAS – two symmetric buildings with two sides equal and one angle equal.
SAS – a tent which has a common perpendicular bisector, resulting in two equal sides and one equal angle.
ASA – the overview of an intersection made of congruent triangles with two equal angles and one equal side.




















































