Introduction
Consider a pack of cards; take any two cards from the pack and examine them.

Both the cards have the same shape and size. If you take any other card from the pack, will it be of the same shape and size as the cards above? Yes. Such objects are called congruent objects.
Let us watch the video and understand some real-life examples of congruent figures.
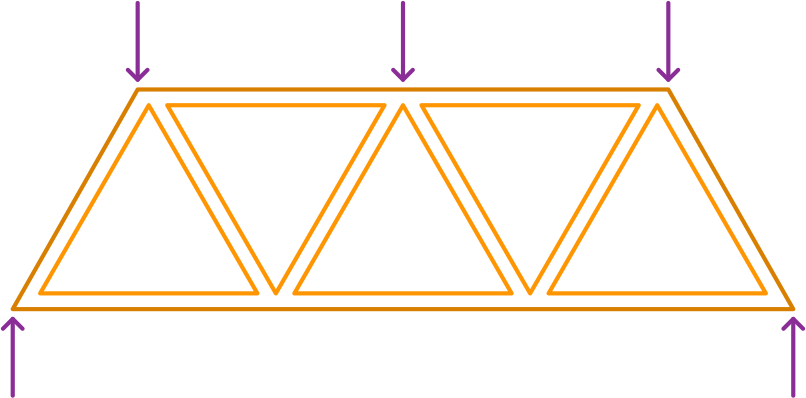
Did you know, the congruency property of triangles is used to build strong, stable structures such as bridges?
Congruent triangles form strong bases which reinforce the structure, and they do not bend or buckle under load, which is why bridges are commonly constructed using congruent triangles.
Triangles also evenly distribute the weight without changing their proportions.
Concepts
The chapter ‘Congruence of Triangles’ covers the following concepts:
Congruence of Plane Figures
Two figures are said to be congruent if they have the same shape and size.
For example, consider these two figures,

Figure F1 is congruent to figure F2. This can be symbolized as F1 ≅ F2.
Congruent figures are exact copies of one another. They have the same shape and size. The method of superposition examines the congruence of plane figures.
Rahul, Diya, and Pooja are making greeting cards for Teacher’s Day. They cut out craft papers into pieces of same size and shape. Diya cut the pieces as follows.

Pooja cut the pieces as follows.

Do you think the pieces are congruent? Let us find by superposition.

When you directly keep one over the other, it may seem that the pieces do not overlap each other exactly. But consider rotating and then overlapping.

Now you can see that the pieces overlap each other exactly. Hence, they are congruent. Now, Rahul cut the pieces as follows.

Let us check if it is congruent with what Diya cut.

Can you say that they are congruent? No.
We cannot change the shape and size of the figure by elongation to check if they are congruent.
You can slide, flip, or rotate one of the figures, and they will remain congruent. For example:

All the three pentagons given above are congruent as they have the same size and shape. Upon rotation and superposition, they overlap each other exactly.
Congruence of Line Segments and Angles
Let us explore line segments and understand the conditions under which two line segments are congruent. Consider these line segments.
Let us use the method of superimposing to identify congruent pairs. If the orientation of the line segment is different, we rotate and superimpose.

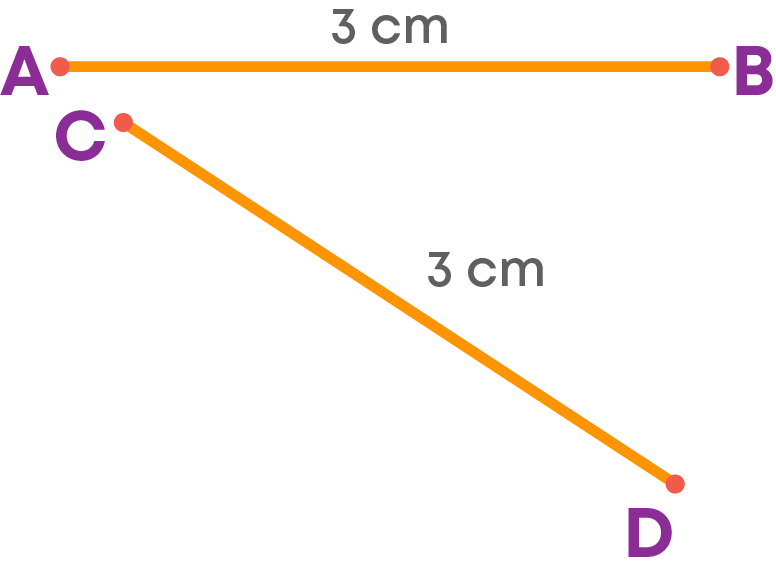
A line segment has only one dimension – length. So even though the line segments are oriented differently, they will be congruent if they have the same length.
If two line segments have the same (i.e., equal) length, then they are congruent. Also, if two line segments are congruent, then they will have the same length. For example, AB and CD are congruent, since they have the same length.
Consider line segments AB, CD, and EF. Let AB = 4 cm, CD = 4 cm, and EF = 5 cm. Let us use the method of superimposing and identify congruent line segments.

We have learnt how to identify congruent line segments, let us now understand the conditions in which two angles are said to be congruent. Consider these angles.
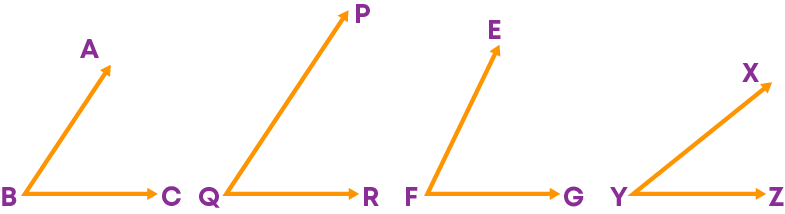
Let us use the method of superimposing to identify congruent pairs of angles. If the orientation of the angle is different, we rotate and superimpose.

Note that while superimposing, the length of the arms of the angle does not matter.
We should check the overlapping of the angle formed by the two arms.
If two angles have the same measure, they are congruent. Also, if two angles are congruent, their measures are same.
For example, angles A, B and C are congruent, since they have the same measure.
Symbolically, ∠A ≅ ∠B ≅ ∠C
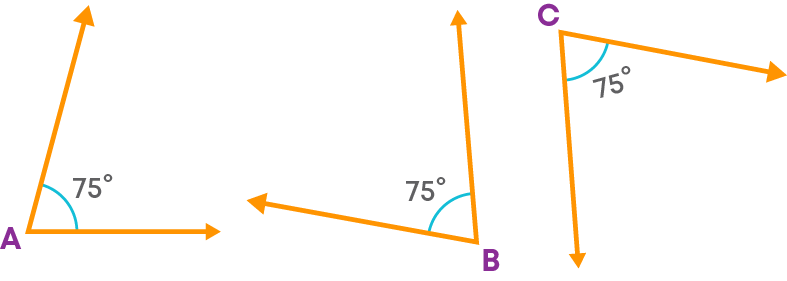
Rishi drew three angles of the following measures:
∠ABC = 75⁰
∠MNO = 75⁰
∠XYZ = 60⁰
He used the method of superimposing to find out congruent angles.

Congruence of Triangles
You know the conditions under which two line segments and two angles are congruent. Also, you know that the six elements of a triangle are its three sides and three angles.
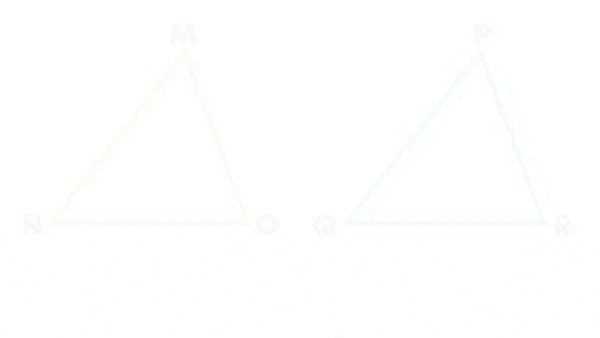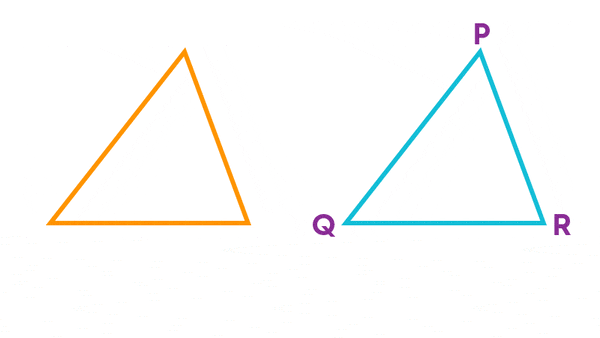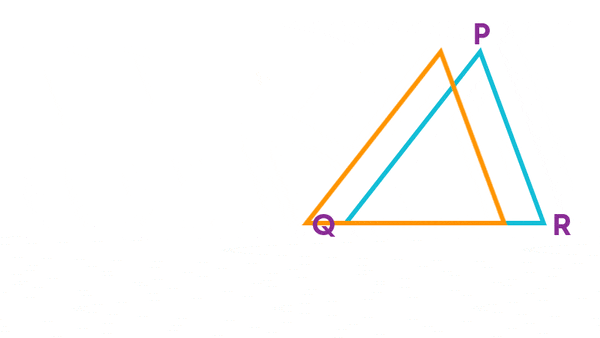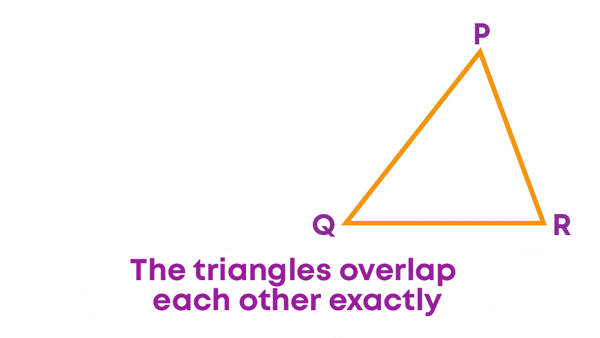
Using this knowledge, let us explore the congruency of triangles. Consider these triangles, ∆MNO and ∆PQR.
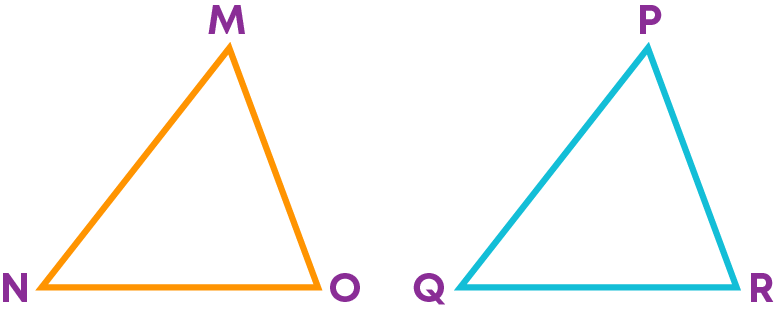
Let us use the method of superposition and check if the triangles are congruent.
From the previous example, you saw that ∆MNO and ∆PQR are congruent. We can write this as ∆MNO ≅ ∆PQR.
When we superimposed ∆MNO and ∆PQR, the triangles overlapped exactly because:
- Vertex P falls on vertex M.
- Vertex Q falls on vertex N.
- Vertex R falls on vertex O.
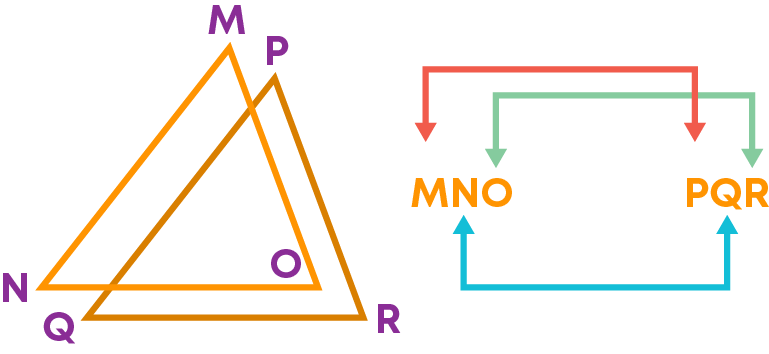
From the above we can see that when ∆MNO ≅ ∆PQR, the vertices that match one another on superimposing are
- M and P
- N and Q
- O and R
Matching vertices are called corresponding vertices.
The sides that match one another on superimposing are
- MN and PQ
- NO and QR
- OM and RP
Matching sides are called corresponding sides.
Similarly, the angles that match one another are
- ∠M and ∠P
- ∠N and ∠Q
- ∠O and ∠R
Matching angles are called corresponding angles.
If two triangles are congruent, then all their corresponding parts are equal in measure. If all the corresponding parts of two triangles are equal, then the triangles are congruent.
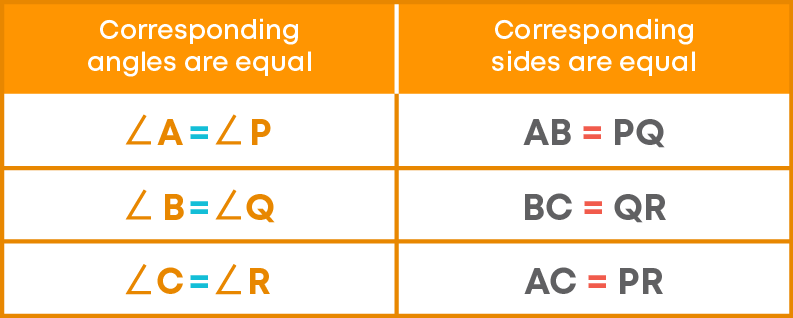
For example, if ∆ABC ≅ ∆PQR, then:
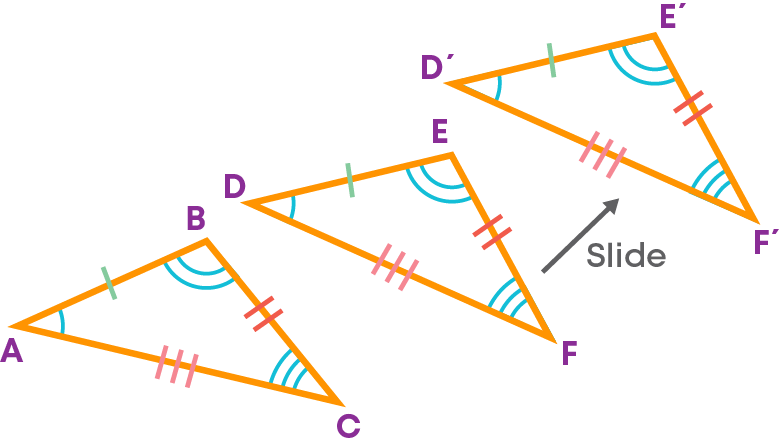
Let us examine congruent triangles ABC and DEF. If you slide ∆DEF up and to right, ∆DEF is still congruent to ∆ABC.
The congruency does not change whether you turn ∆DEF or flip ∆DEF. ∆ABC is still congruent to ∆DEF.
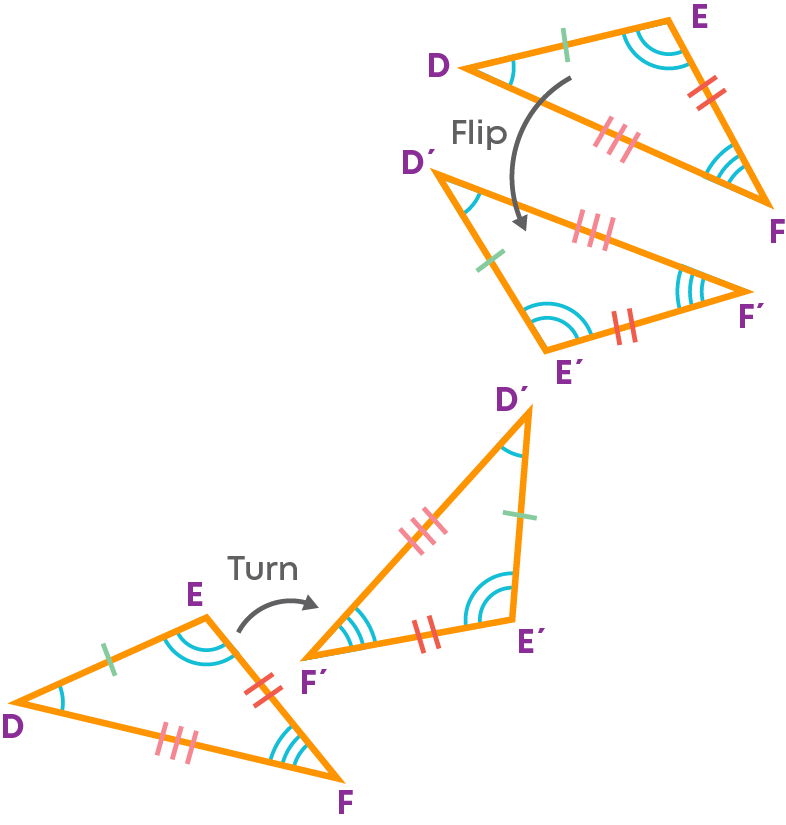
If you slide, flip, or turn a triangle, the size and shape do not change.
Consider two windows.

We must check if the windows are of the same shape and size. Or in other words, are the windows congruent? Can we overlap the windows by superimposing? No! This is not practically possible. We may need to measure the sides of the windows and check whether they are equal or not. Hence, the equality of corresponding sides is important for congruence of two shapes.
Consider these triangles:
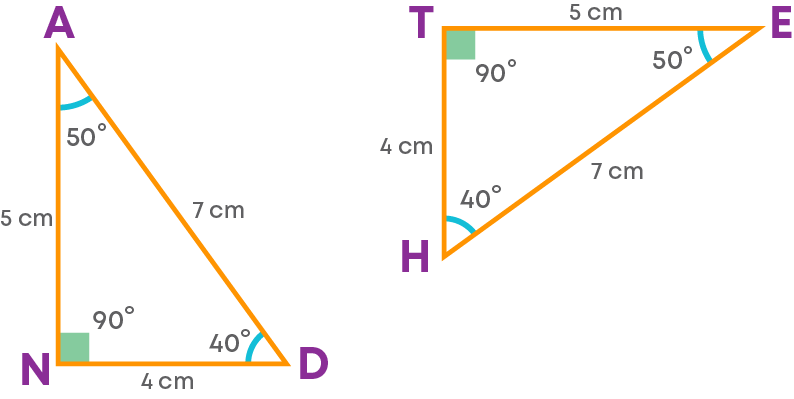
Let us check if these triangles are congruent by the method of superimposing.
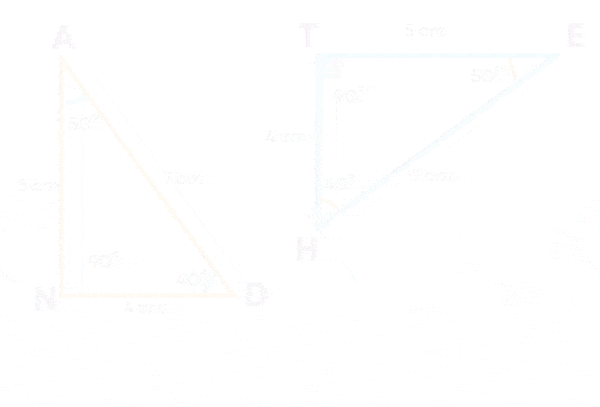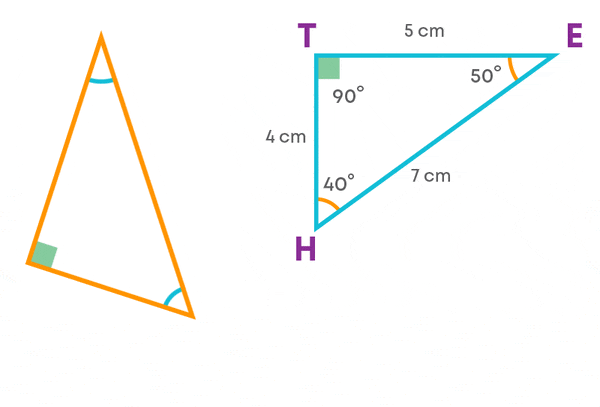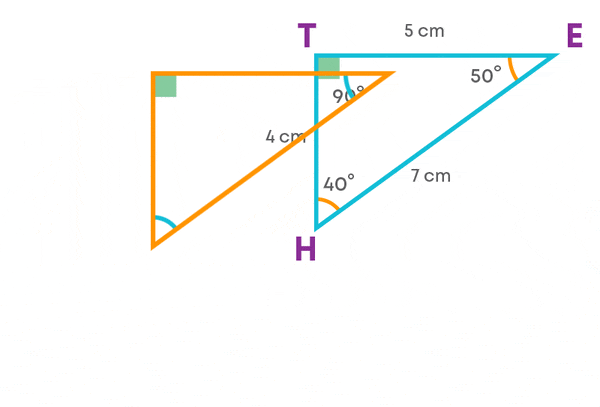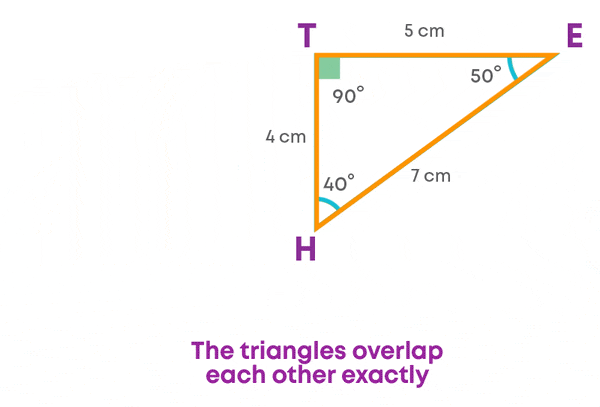
What do you notice? The triangles are congruent. While superimposing, we rotated the triangle so that the corresponding parts match.
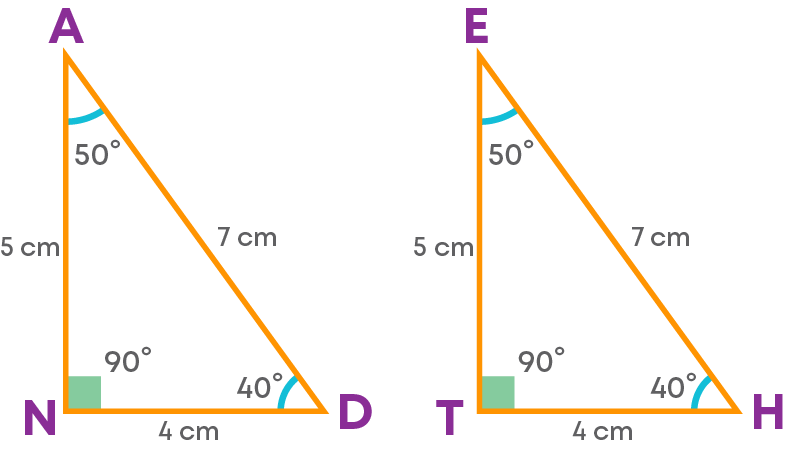
Do you think the triangles will overlap exactly if you do not rotate? No.
This is because while talking about congruence of triangles, not only the measures of angles and lengths of sides matter, but also the matching of vertices. This matching is called correspondence. It is denoted by the symbol ‘↔’
We can say that the triangles are congruent under the correspondence AND ↔ ETH.
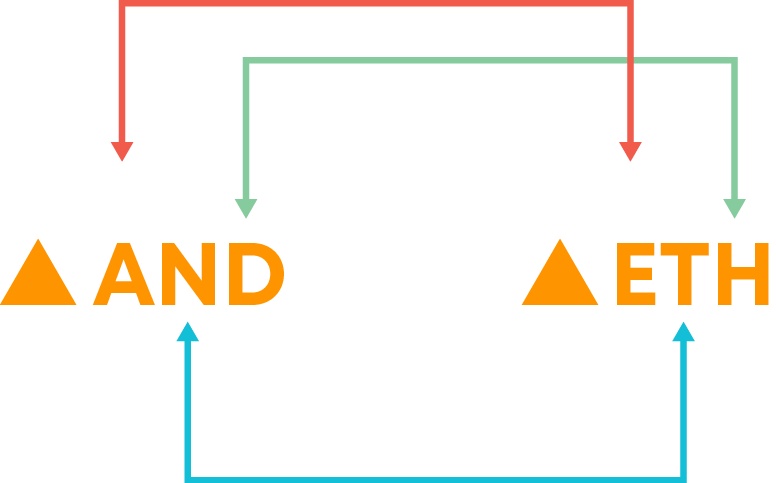
Let us list the corresponding parts.
The corresponding vertices are:
- A ↔E
- N ↔T
- D ↔H
The corresponding sides are
- AN ↔ TE (= 5cm )
- ND ↔ TH (= 4 cm)
- AD ↔ EH (= 7 cm)
The corresponding angles are
- ∠A ↔ ∠E (= 50°)
- ∠N ↔∠T (= 90°)
- ∠D ↔ ∠H(=40° )
If a triangle can be translated, rotated, or reflected onto another triangle so that all the vertices correspond, the triangles ae congruent triangles. The parts of congruent triangles that “match” are called corresponding parts.
Remember!
- Arcs are used to show which angles are equal. Slash marks are used to show which sides are equal.
- Correspondence is denoted by ‘↔’
- Congruence is denoted by ≅
Congruence Criteria
A triangle has three sides and three angles. For two triangles to be congruent, there should be equality of these six elements. The congruence criterion gives a short-cut method to check for congruence with any three elements. Let us explore more such congruence criterion.

For example,
AB = PQ, BC = QR, AC = PR
Hence, ∆ABC ≅ ∆PQR
The order of the letters in the names of congruent triangles displays the corresponding relationships. For example:

When you write ∆MNO ≅ ∆PQR, you know that:
- M lies on P
- N on Q
- O on R
- MN along PQ
- MO along PR
- MO along QR
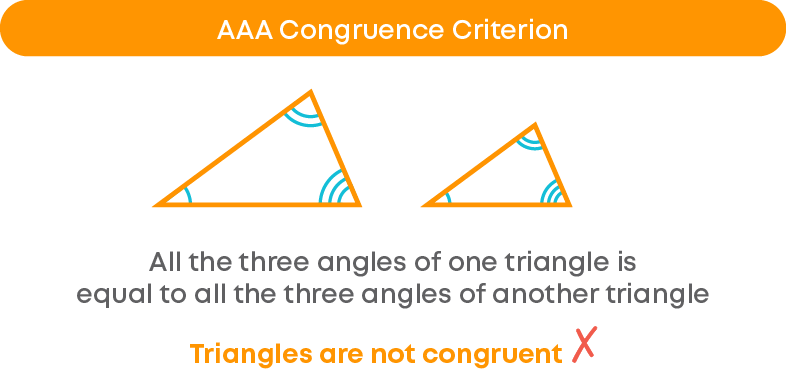
Remember, there does not exist AAA congruence criterion. Even though all the three angles of one triangle is equal to all the three angles of another triangle, the triangles need not be congruent as the length of the sides may be different.
The next criterion is called Side-Angle-Side criterion or SAS congruence criterion.

For example,
RP = US, PQ = ST, ∠P = ∠S
Hence, ∆RPQ ≅ ∆UST
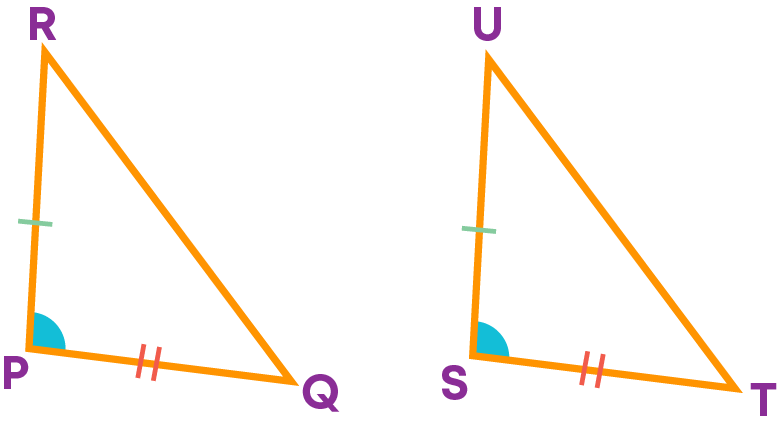
Consider these triangles, ∆ABC and ∆PQR.
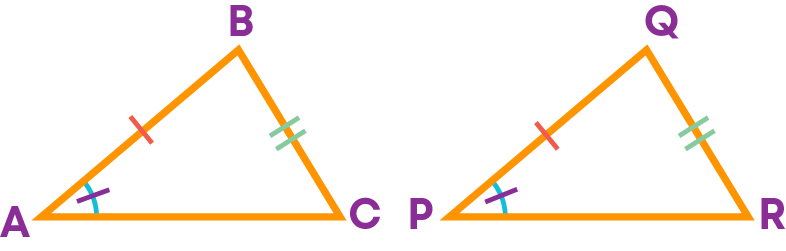
Can you say that these triangles are congruent? No. It is given that AB = PQ, BC = QR, and the non-included angle A = angle P. Do you think that given two sides and a non-included angle is enough to prove congruence?
There is another pair of triangles possible with the same measure. Observe these triangles:
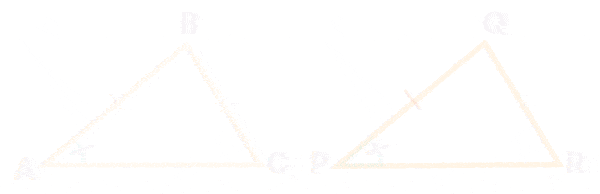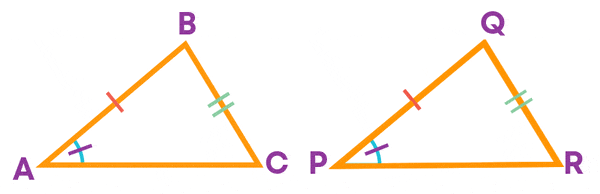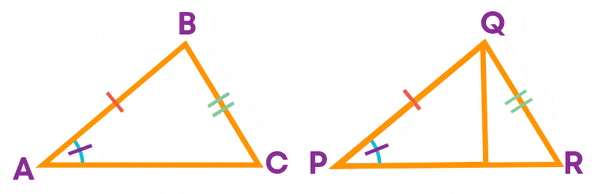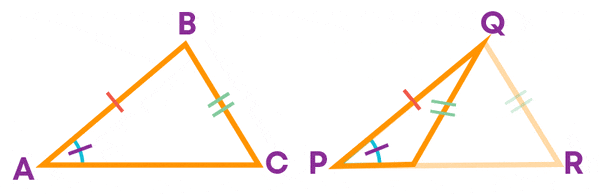
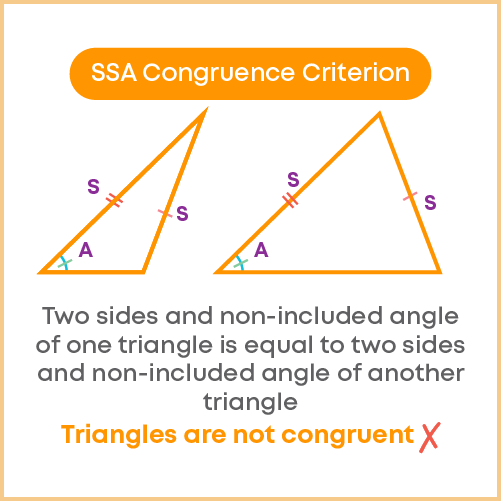
Beware! There is no SSA congruence criterion.
The angle (A) should be an included angle for two triangles to be congruent.
So, for two triangles to be congruent, two pair of corresponding sides and the included angle must be equal.
The next criterion is called Angle-Side-Angle criterion or ASA congruence criterion.
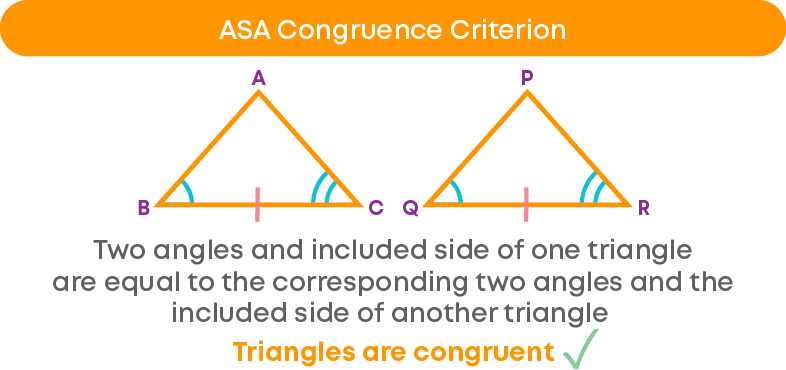
For example,
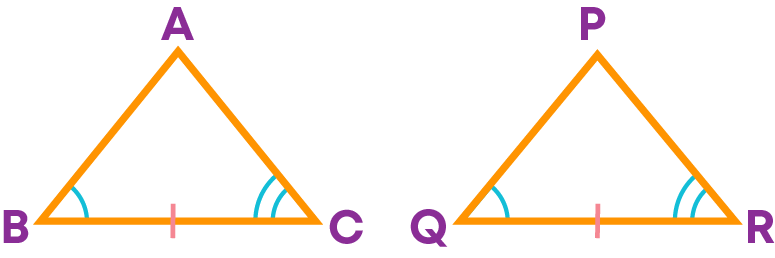
∠B = ∠Q, BC = QR, ∠C = ∠R
Hence, ∆ABC ≅ ∆PQR
Now observe the triangles.

We can use ASA congruence criterion and say that the triangles OPQ and IJK are congruent.
Given two angles of a triangle, you can always find the third angle of the triangle.
So, whenever, two angles and one side of one triangle are equal to the corresponding two angles and one side of another triangle, you may convert it into ‘two angles and the included side’ form of congruence and then apply the ASA congruence rule.
In other words, we can say that AAS congruence criterion exists.

The next criterion is called Right angle -Hypotenuse-Side criterion or RHS congruence criterion.
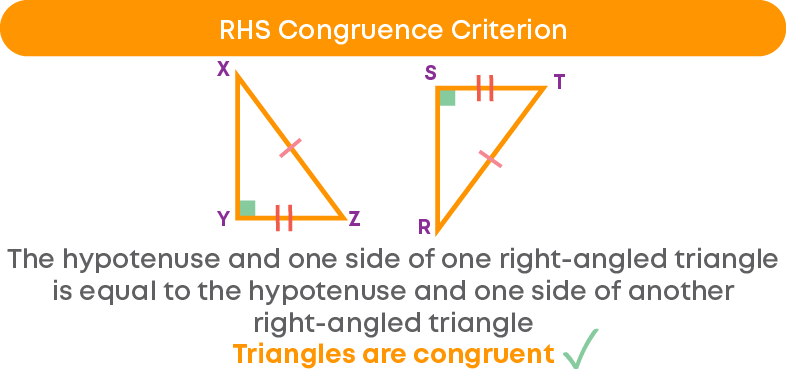
For example,

∠B = ∠Q = 90⁰
Hypotenuse AC = PR
Side BC = QR
Hence, ∆ABC ≅ ∆PQR
Common Errors
The following are topics in which students make common mistakes when dealing with congruence of triangles:
- 1. AAA congruence
- 2. Importance of included angles in SAS congruence criterion
- 3. Symbolic representation of congruence
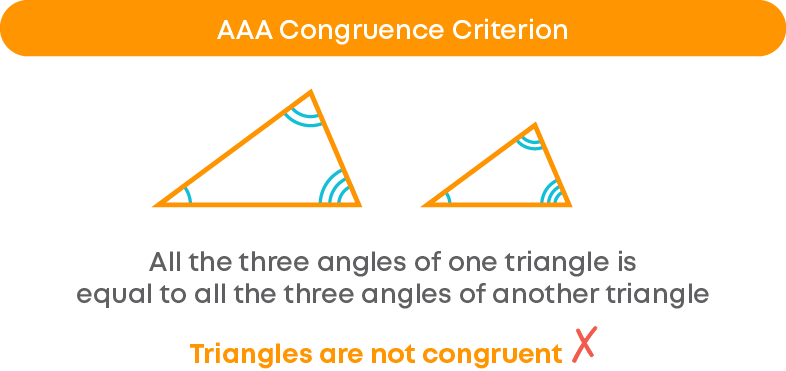
AAA Congruence
There are 2 triangles, ∆ABC and ∆PQR.
∠A = ∠P = 80°.
∠B = ∠Q = 60°.
∠C = ∠R = 40°.
Can you say that ∆ABC ≅ ∆PQR by AAA congruence criterion? No! Even though the triangles have the same angles of the same measure, their sides need not be the same, hence, they need not be congruent.
Importance Of Included Angles In SAS Congruence Criterion
Consider 2 triangles, ∆ABC and ∆PQR.
∠A = ∠P
AB = PQ
BC = QR
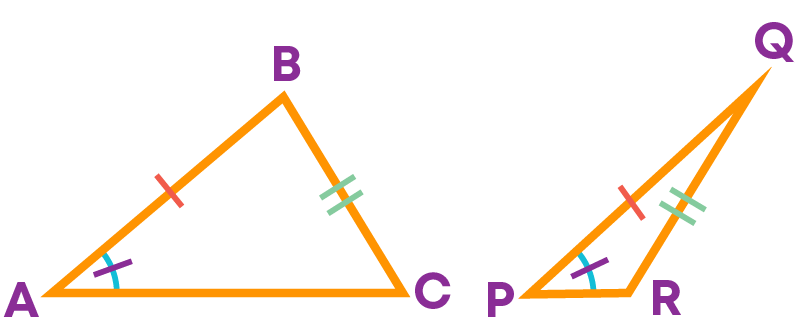
Can you say that the given triangles are congruent? No! We cannot conclude that the given triangles are congruent since equal angles are not included.
Hence, while proving that two triangles are congruent using the SAS congruence criterion, make sure that the angle is included between the sides.
Symbolic Representation Of Congruence
You know that the two triangles ABC and PQR shown below are congruent by the SSS congruence criterion.
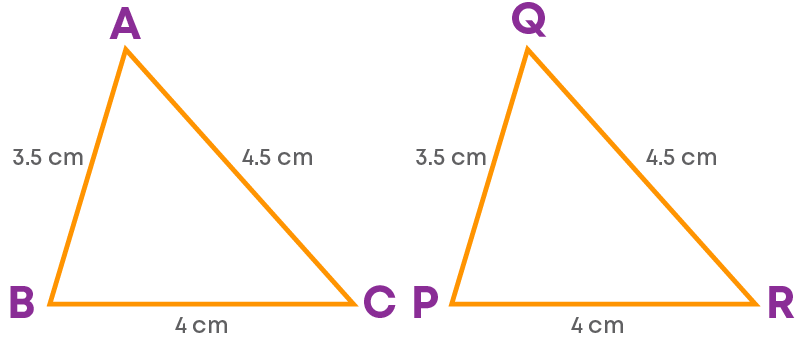
To represent their congruence relation symbolically, you should know the corresponding vertices.
From the given figure, it is clear that,
- A ↔ Q
- B ↔ P
- C ↔ R
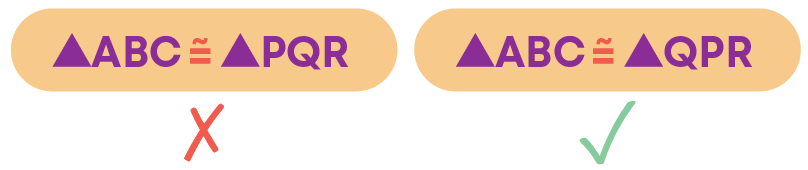
Hence, ∆ABC ≅ ∆QPR.
Conclusion
Now that you understood congruence, can you identify which of the following patterns are made up of congruent shapes?
A

B

C

D





















































