Introduction
We see that if length ‘l’ or breadth ‘b’ of any geometrical figure is taken as meter (m) or centimeter (cm) , then
- The unit of measurement for its area is taken as square meter (m2) or square centimeter (cm2)
- The unit of measurement for its perimeter is taken as meter (m) or centimeter (cm)
Suppose we have a huge triangular garden, and we want to put a fence around it using barbed wire. What will help us to find the length of the barbed wire required? Is it the perimeter of the triangular garden? Yes.
Now, if a gardener wants to redo the garden by putting down new, fresh grass on the land, we need to find the area of the triangular garden.

We know that if ‘b’ is the base and ‘h’ is the height of a triangle then the area of the triangle is 1 2 × b × h
Now, what if we do not know the height but know the three sides of this triangular garden? Can we still find its area? Let us watch a video to understand this.
From the video, we understand that we can find the area of any triangle even if its height is unknown but three of its sides are known. This can be done using Heron’s formula.
We can find the area of a triangle when we know:
- 1. The lengths of a side and its corresponding altitude
- 2. The lengths of the three sides
To find the area when we know the length of a side and its corresponding altitude, we use the formula:
Area = 1 2 × base × height
When we know the lengths of three sides, we use Heron’s formula to find the area.
Concepts
The chapter ‘Heron’s Formula’ covers the following concepts:
Area of Triangles
We can find the area of a triangle using the area of a rectangle. Consider:
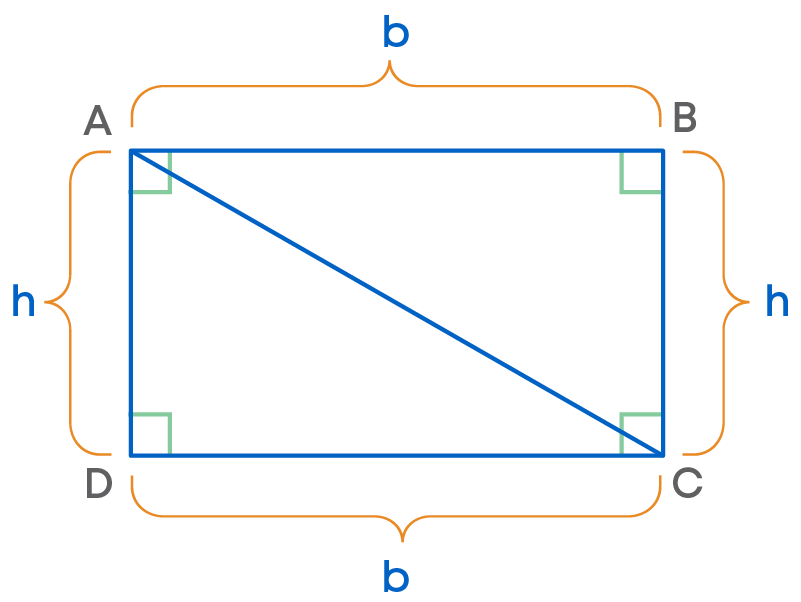
We see that if AC is the diagonal of rectangle ABCD having area b × h, then
Area of ∆ABC = ∆ADC = 1 2 × b × h
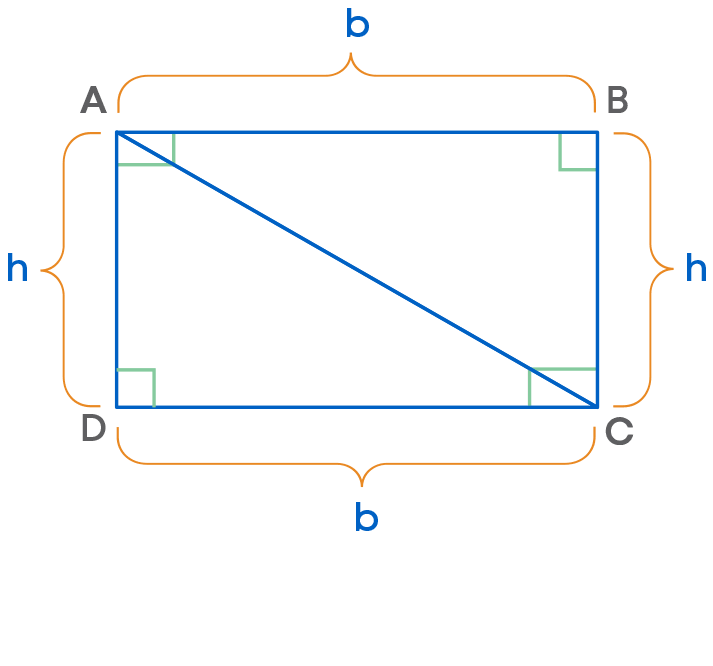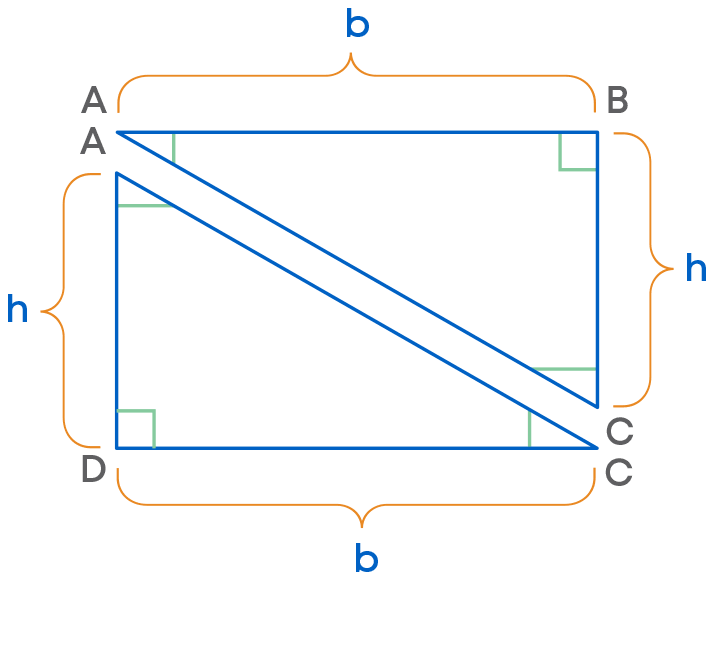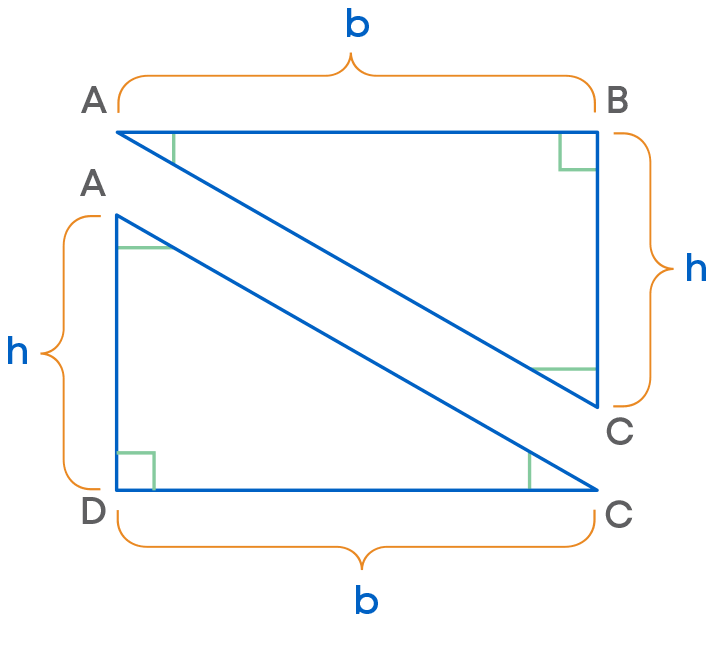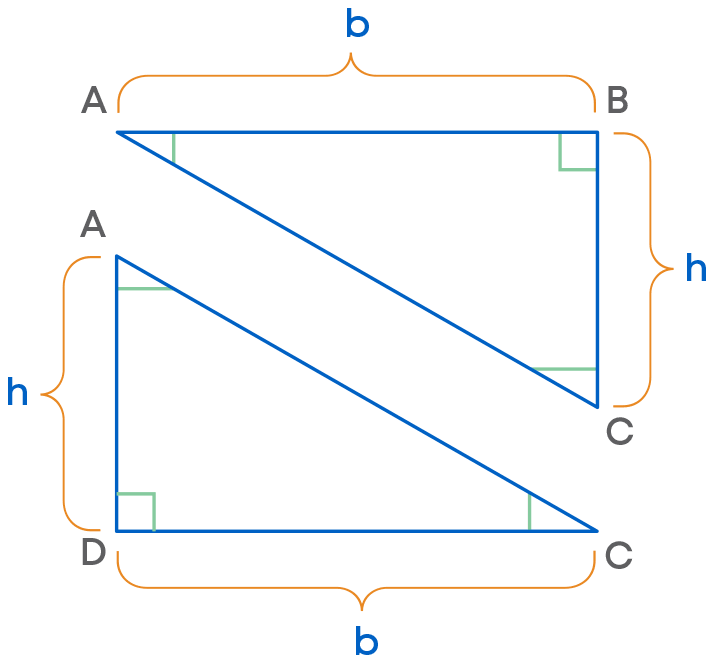
If base = b and height = h in ∆ABC, then area of ∆ABC = 1 2 × b × h
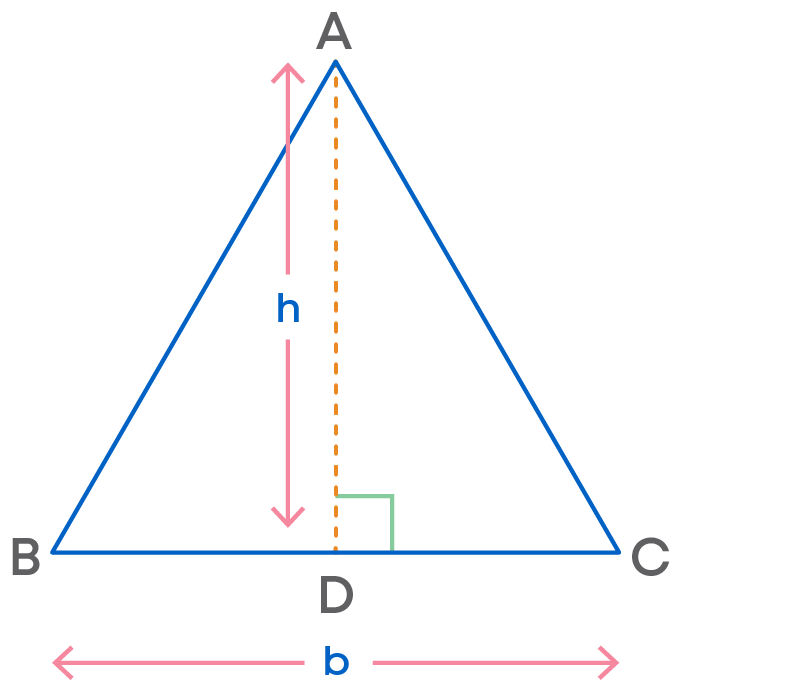
Let us apply this formula to solve some problems. Suppose Sara is sitting in a right triangular garden and wants to find its area.
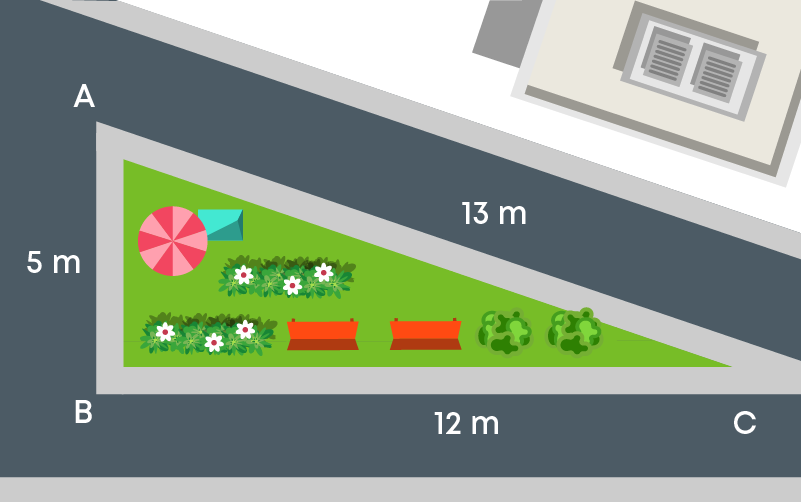
In this case, one of the two sides containing the right angle can be taken as base and the other as the height.
Suppose she takes base = b = 12 m and height = h = 5 m.
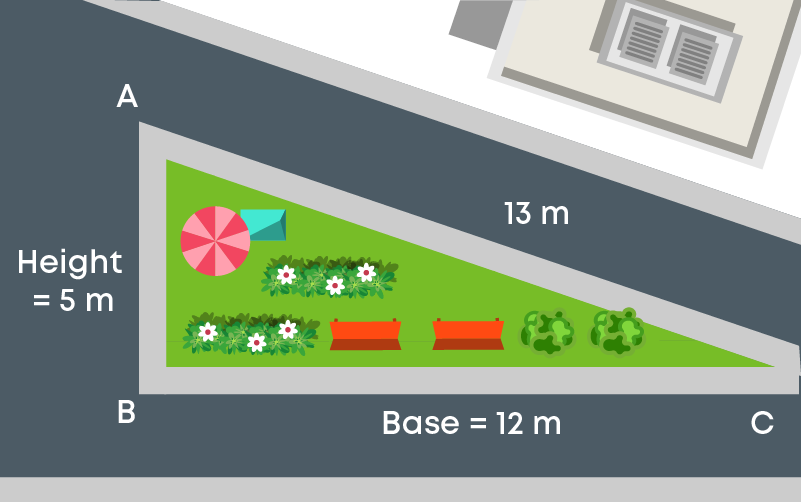
Therefore, area of right-triangular garden = area of ∆ABC
= 1 2 × b × h = 1 2 × 12 m × 5 m = 30 m2
Note that she could also take 5 m as the base and 12 m as height.

Suppose Sara has a triangular sheet of paper having sides 6 cm, 6 cm, and 10 cm.
(AB = 6 cm, BC = 10 cm, and AC = 6 cm)
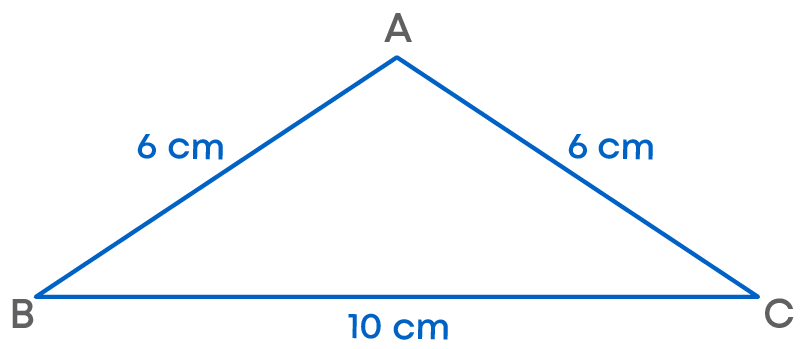
To find its area, she needs its base and height. Clearly, she can take the largest side as its base.
To solve this problem, first construct AD⊥BC.
Since ABC is an isosceles triangle with AB = AC, D is the midpoint of side BC .

As D is the midpoint of side BC, BD = 5 cm ------ (1)
As AD⊥BC, ∆ABD and ∆ACD are right-angled triangles.

By Pythagoras theorem for ∆ABD,
AB2 = BD2 + AD2 ------ (2)

So, height of ∆ABC = AD
= √AB2 – BD2 (from 2)
= √62 – 52
= √36 – 25
= √11 cm
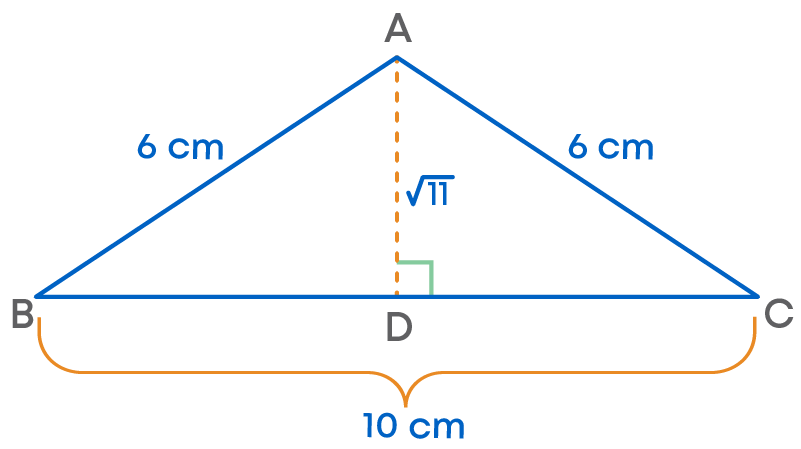
So, area of ∆ABC = 1 2 × b × h = 1 2 × 10 × √11
= 5√11 cm2
We can draw the perpendicular height from any vertex to the opposite base of a triangle.
In an isosceles triangle, the perpendicular height drawn to the base between the equal sides will divide the base into two equal parts.
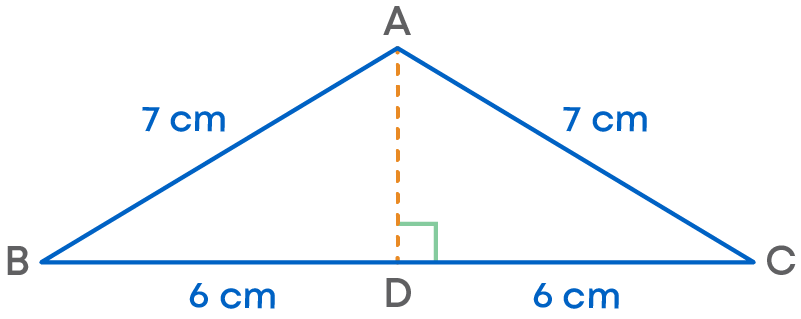
In the isosceles triangle ABC, the perpendicular drawn to the base BC lies between the equal sides AB and AC. AD divides BC into two equal parts.
That is, BD = DC = 6 cm
In other words, D is the midpoint of BC.
Now, suppose Sara has a triangular sheet of paper having each side 20 cm.
(PQ = QR = PR = 20 cm)
To find its area, she needs to know its height. Can you find its height?
To find the area of a triangular sheet of paper having each side 20 cm, we need its height.
We see that height of triangle PQR = PS = h = 10√3 cm and base QR = b = 20 cm.

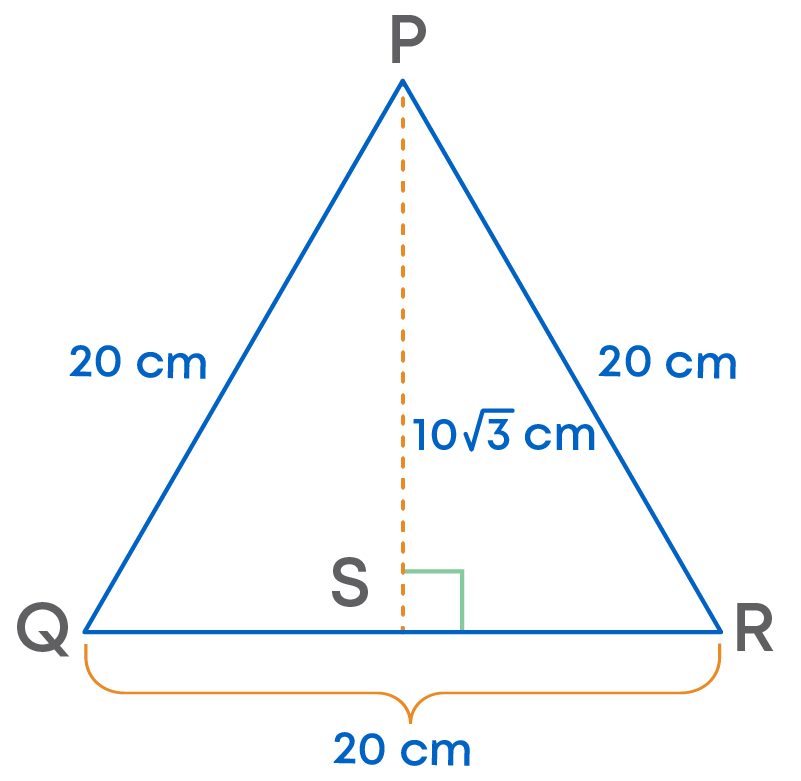
So, area of triangle PQR = 1 2 × b × h = 1 2 × 20 × 10√3 = 100√3 cm2
Area of Triangles and Quadrilaterals Using Heron’s Formula
Suppose you want to find the area of a triangular park PQR whose sides are 82 m, 80 m, and 30 m.
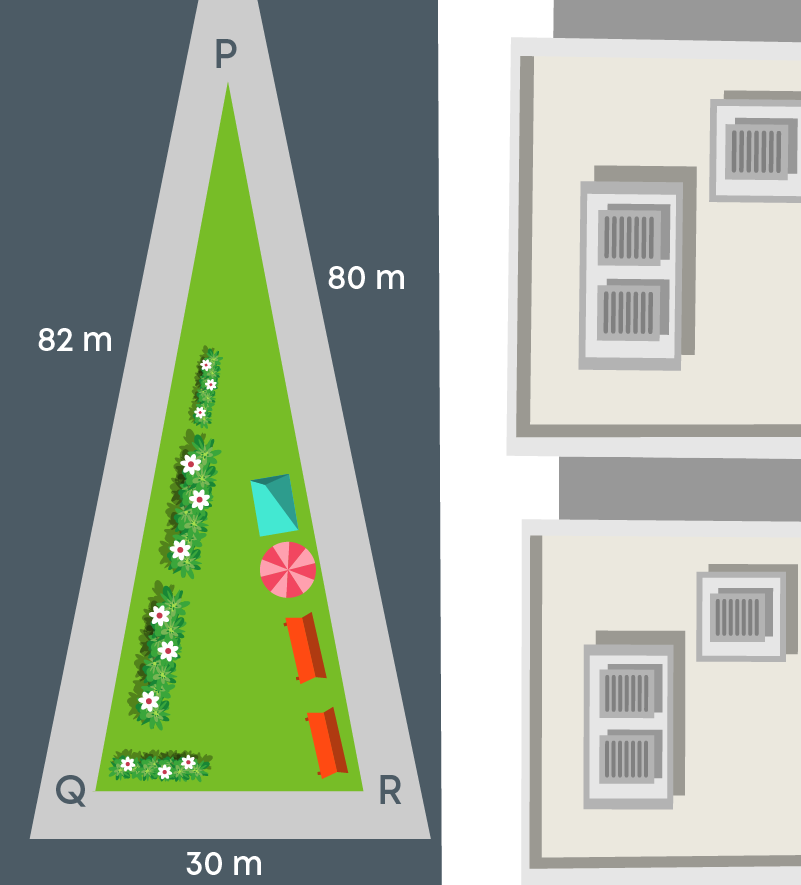
If you want to apply the area formula, you need to calculate its height. Let us draw a perpendicular PS from vertex P to the base QR of ∆PQR.
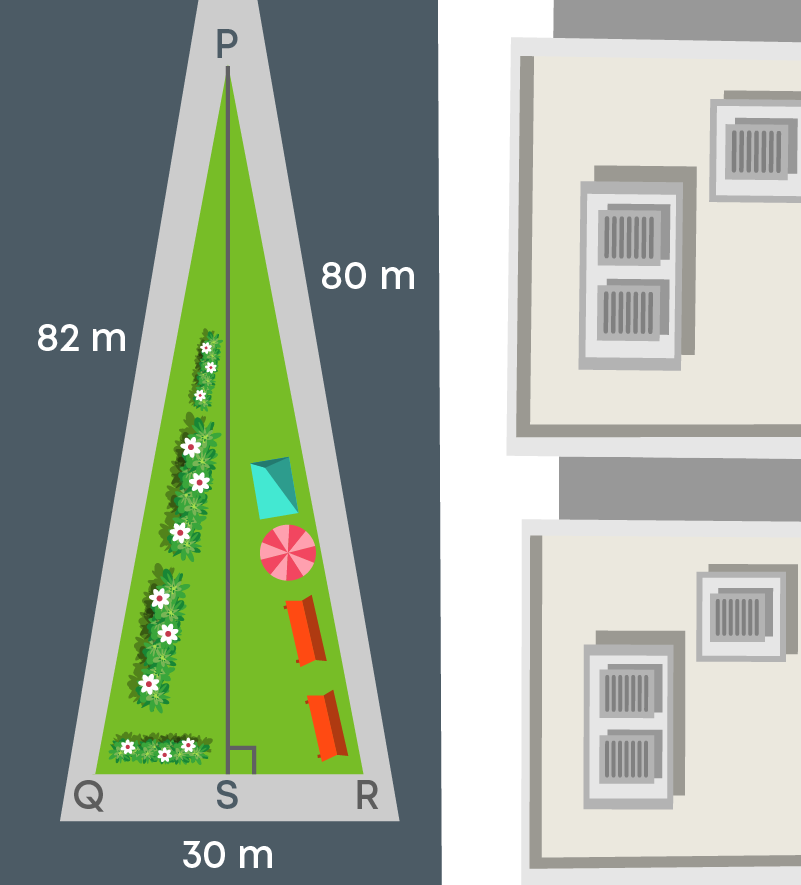
But this perpendicular PS does not bisect the base QR. So, it is not possible to find the measure of QS or SR. Hence, we cannot apply Pythagoras theorem to find its height.
Also, we do not have any other information to find its height. So, to find its area we need a formula in terms of its sides.
It is practically difficult to find the height of huge triangular fields, parks, etc.
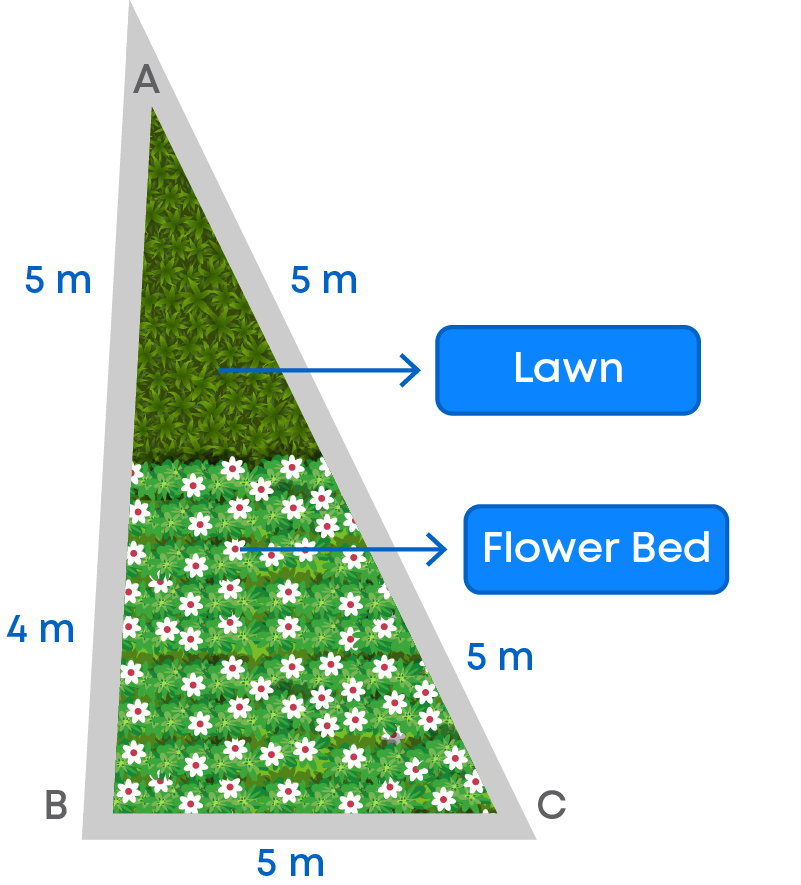
You know the sides of the field but need to calculate the area. A different formula is devised to find the area in terms of sides.
This formula was devised by Heron and is known as Heron’s formula. The formula is as follows:

This formula is helpful where it is not possible to calculate the height of the triangle.
Let us apply Heron’s formula to find the area of the triangular park PQR.

Let us take a = 82 m, b = 80 m, and c = 18 m, so the semi-perimeter is:
s = a+b+c 2 = 82 + 80 +18 2 m = 90 m
s – a = (90 – 82) m = 8 m
s – b = (90 – 80) m = 10 m
s – c = (90 – 18) m = 72 m
∴ the area of park PQR
= √s(s – a)(s – b)(s – c)
= √90 × 8 × 10 × 72 m2
= 720 m2
In this way, we can find the area of any triangle given its sides.
Let us apply Heron’s formula on a triangle whose three sides are 21 cm, 11 cm, and 16 cm. We get its semi-perimeter = 24 cm.
Also, its area is given by √24(24 – 21)(24 – 11)(24 – 16)
Let us now simplify this expression.
√24(24 – 21)(24 – 11)(24 – 16) cm2
√24× 3 × 13 × 8 cm2
24√13 cm2
Hence, area of the given triangle is 24√13 cm2.
We see that the area of a triangle can be found when its three sides are given. But can you find the area of a triangle when only two of its sides and its perimeter are given?
Let us try to solve this problem:
Find the area of a triangle XYZ such that XY = 11 cm, YZ = 8 cm, and perimeter is 32 cm.

We know that perimeter of triangle XYZ = (XY + YZ + XZ)
But perimeter = 32 cm
So, 32 = 11 + 8 + XZ
XZ = 32 – 11 – 8 = 13 cm.
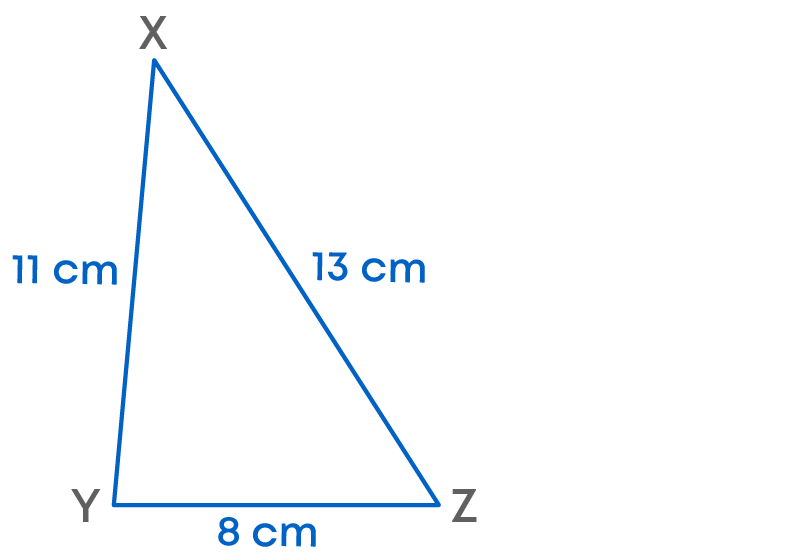
Now, let us apply Heron’s formula. Let a = 11 cm, b = 8 cm, and c = 13 cm.

s = 1 2 × 32 = 16 cm

The area of triangle XYZ = √16(16 – 11)(16 – 8)(16 – 13) cm2
√16 × 5 × 8 × 3 cm2
8√30 cm2
Let us learn how to apply Heron’s formula for solving a real-life problem.
A triangular plot XYZ has sides 120 m, 80 m, and 50 m.
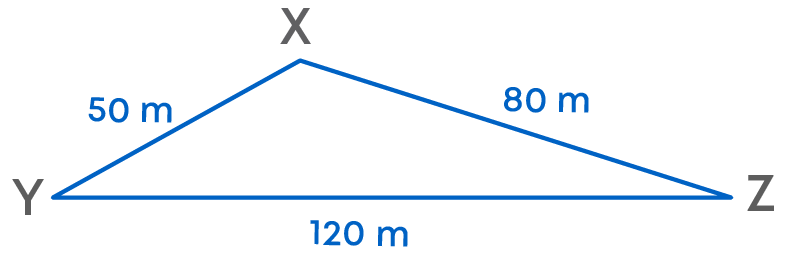
Ram wants to plant grass inside it. How much area does he need to plant?
Let us apply Heron’s formula to find the area of plot XYZ.

Let a = 50 m, b = 80 m and c = 120 m.
Semi-perimeter of plot XYZ = s = a+b+c 2 = 50 + 80 +120 2 m = 125 m
The area of triangle XYZ = √125(125 – 50)(125 – 80)(125 – 120) m2
√125 × 75 × 45 × 5 m2
375√15 m2
The area Ram needs to plant is 375√15 m2.
Now, Ram wants to put a fence all around the plot. Find the cost of fencing wire at the rate of ₹35 per meter, leaving a space 4 m wide for a gate on the largest side.

The perimeter of the plot XYZ = XY + YZ + XZ
= 50 + 80 + 120
= 250 m
Width of the space to be left for gate = 4 m
So, the length of the fencing wire = 250 – 4 = 246 m
So, the cost of fencing wire at the rate ₹35 per meter = ₹35 × 246 = ₹8,610.
We can find the area of a rectangle by splitting it into two right triangles with the help of one diagonal. Example:
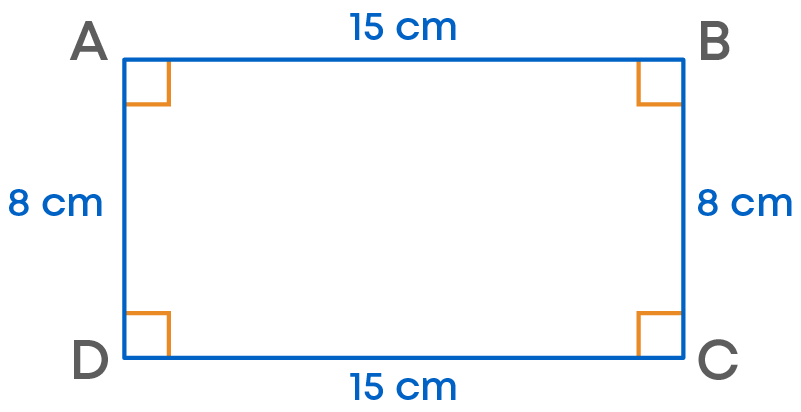
For this, we draw diagonal AC.
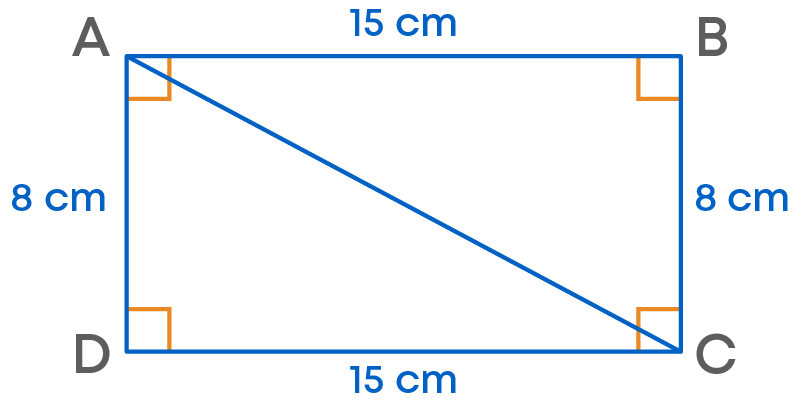

We have area of triangle ADC = triangle ABC
So, area of rectangle ABCD = area of triangle ADC + triangle ABC = 2 × area of ∆ADC
= 2 × ( 1 2 × b × h)
= 2 × ( 1 2 × 15 × 8)
= 120 cm2
Now, consider a quadrilateral ABCD with sides measuring 10 cm, 9 cm, 7 cm, and 12 cm as shown in the figure. Diagonal BD measures 4 cm.
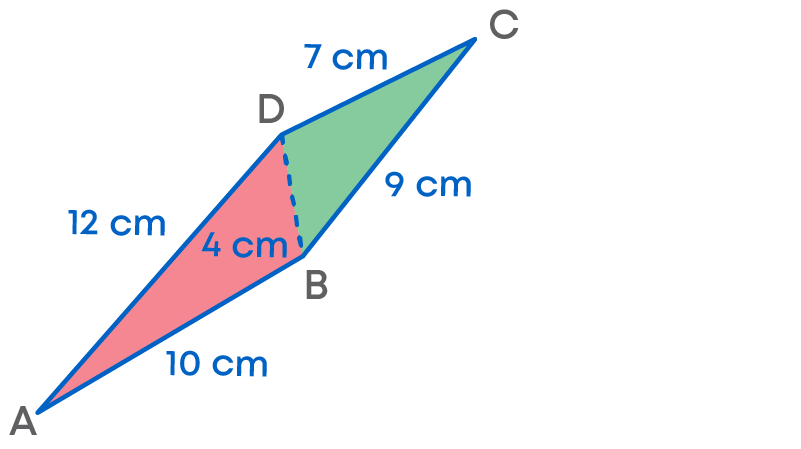
Let us understand how to find the area of such irregular quadrilateral using Heron’s formula.
We can see here that the quadrilateral ABCD is divided into two triangles ABD and BCD. We find the areas of these triangles to find the area of the quadrilateral.
We apply Heron's formula to find the areas of triangles ABD and BCD.
Finding area of ∆ABD:
Let a = 10 cm, b = 4 cm, and c = 12 cm
Semi-perimeter of ∆ABD = a+b+c 2 = 10 + 4 +12 2 cm = 13 cm
Area of ∆ABD = √13(13 – 10)(13 – 4)(13 – 12) cm2
√13 × 3 × 9 × 1 cm2
3√39 cm2
= 18.72 cm2
Finding the area of ∆BCD:
Semi-perimeter of ∆BCD = a+b+c 2 = 9 + 4 + 7 2 cm = 10 cm
Area of ∆BCD = √10(10 – 9)(10 – 4)(10 – 7) cm2
√10 × 1 × 6 × 3 cm2
6√5 cm2
= 13.62 cm2
Finding the area of the quadrilateral ABCD = Area of ∆ABD + Area of ∆BCD
= 32.34 cm2
We can find the area of a quadrilateral by dividing it into triangles and using Heron’s formula. The strategy to apply the formula and solve is as follows:
- Split the given quadrilateral (whose area is to be found out) into appropriate triangles or regular polygons such as square, rectangle, etc.
- Use the formula 1 2 × b × h or Heron’s formula to find the area of these triangles.
Add the area of these triangles to find the area of the quadrilateral.
Common Errors
The following are topics in which students make common mistakes when dealing with Heron’s formula:
- 1. Application of Heron’s formula
- 2. Terms involved in Heron’s formula
- 3. Finding the area of a rhombus
Application of Heron’s formula
Heron’s formula is applicable only on triangles. So, to find the area of a quadrilateral, do not directly apply Heron’s formula on the quadrilateral. Divide the quadrilateral into two triangles and then apply Heron’s formula on the two triangles.

Terms Involved In Heron’s Formula
Heron’s formula for finding the area of a triangle = √s(s – a)(s – b)(s – c)
Here, a, b and c are the lengths of sides of the triangle.
‘s’ is semi-perimeter of the triangle, i.e., half of the perimeter of the triangle.
Do not substitute the perimeter in place of ‘s’. Divide the perimeter by 2 and substitute the result.

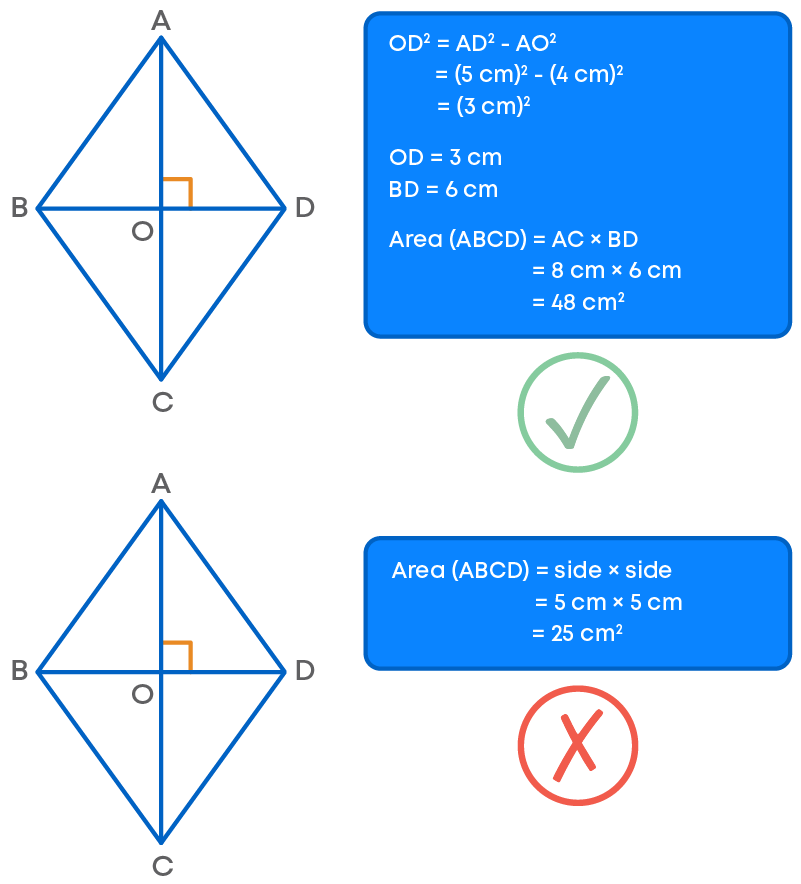
Finding The Area Of A Rhombus
To find the area of a rhombus when the length of its each side and a diagonal are given, we must calculate the length of the other diagonal using Pythagoras theorem. Then, half of the product of the diagonals gives the area of the rhombus.
Finding the square of the side (or multiplying the side by the side) of the rhombus will not give us the area of the rhombus.
For example, find the area of a rhombus with each side measuring 5 cm and the longer side measuring 8 cm.
Conclusion
Now that you know Heron’s formula, can you solve this riddle?
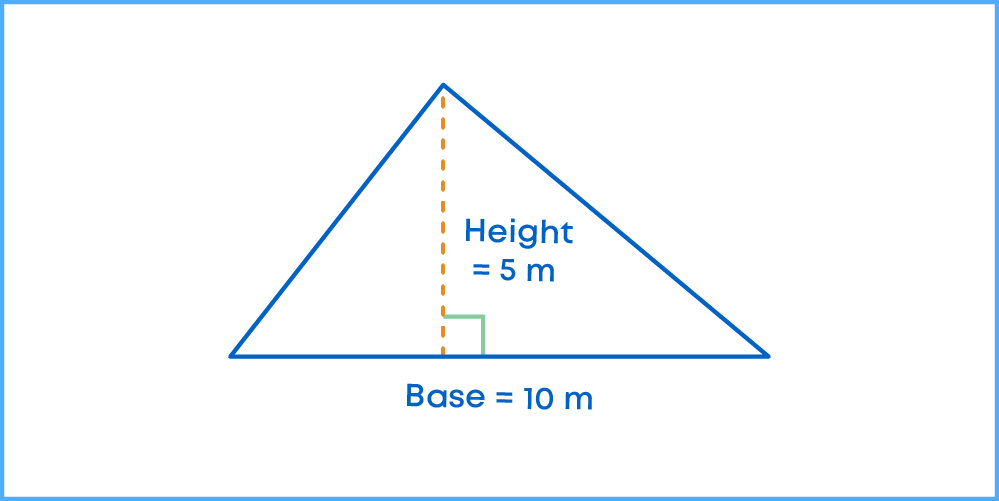
Raj wants to paint a triangular board for a project having base = 10 m and height = 5 m.
What is the area that needs to be painted?
If the cost of painting per m2 of the board is ₹12, what will be the total cost of painting the board?