Introduction
We can see lines and angles around us in many places. Why do we need lines and angles? Watch this video to understand why lines and angles are important.
What is a line ? In geometry, a line segment has two end points. If we extend the two end points endlessly in both directions we get a line. Hence, a line has no end points. For example,

Here, A and B are the points on the line AB.
What is an angle? In geometry, an angle can be defined as the figure formed by two rays starting from a common end point. An angle is represented by the symbol ∠. For example,
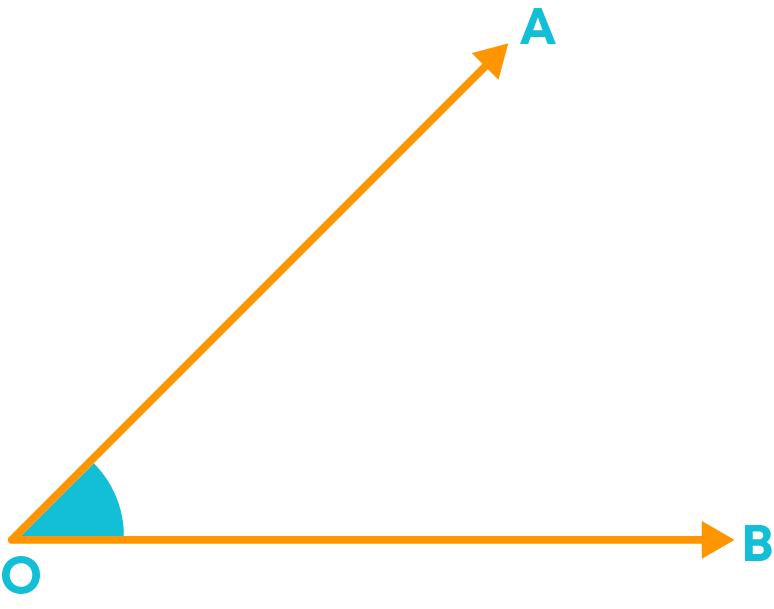
Here ∠AOB is formed by the two rays OA and OB at a common end point O.
We can find angles formed in different polygons also. For example, consider a triangle ABC.
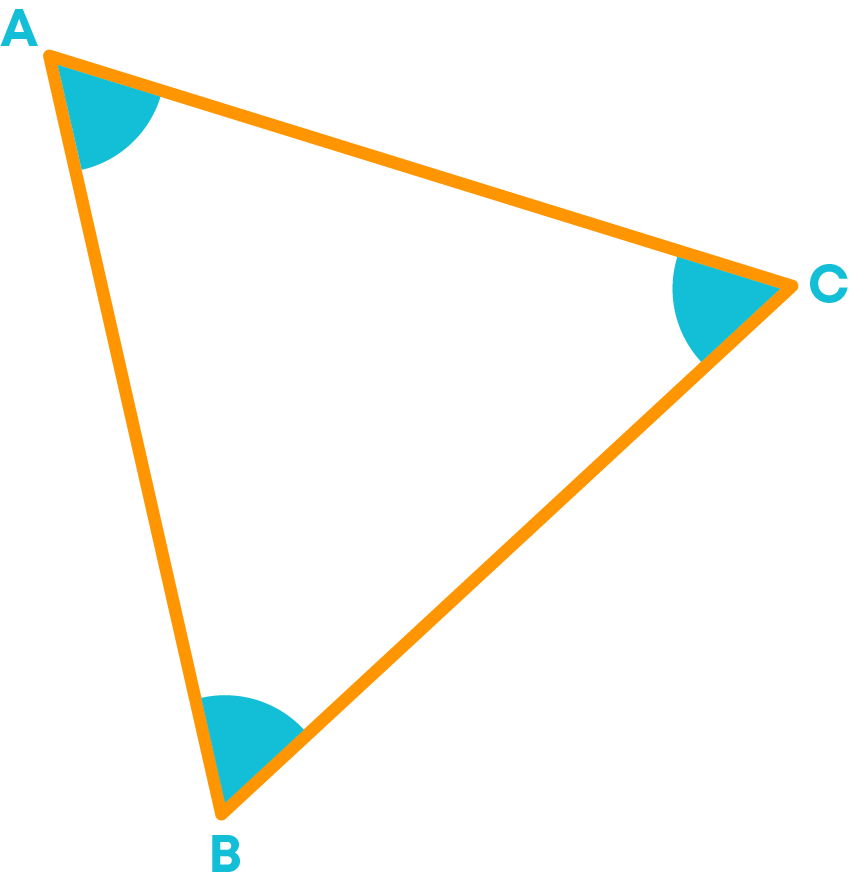
Here the angle ∠ABC is formed when line segments AB and BC intersect at B. ∠BAC is formed when line segments AB and AC intersect at A. ∠ACB is formed when line segments AC and BC intersect at C.
Also, angles are measured in degrees, using a protractor.
Concepts
The chapter ‘Lines and Angles’ covers the following concepts:
Pair of Angles
Two angles are said to be complementary when they add up to 90 degrees. In other words, when the sum of the measures of two angles is 90°, the angles are called complementary angles. For example, here we can see angles 40° and 50°.

We say 40° and 50° are a pair of complementary angles. Also, we say 40° is the complement of the angle 50° and 50° is the complement of the angle 40°. That is, whenever the angles are said to be complementary, we call each angle as the complement of the other.
If one of the angles is 23°, then find the measure of the other complementary angle.
How can you find the other angle? It is given that one of the angles is 23°. We know that the sum of measures of the complementary angle is 90°. Let us take the unknown angle as ‘x.’ Now, we have x + 23° = 90°. From this we get, x = 90° - 23° = 67°. Hence, the measure of the other complementary angle is 67°.
Two angles are said to be supplementary when they add up to 180 degrees. In other words, when the sum of the measures of two angles is 180°, the angles are called supplementary angles. For example, let us see the pair of angles 130° and 50°.

We call 130° and 50° as supplementary angles. Here, 130° is the supplement of the angle 50°, and 50° is the supplement of the angle 130°. That is, whenever the angles are said to be supplementary, we call each angle as the supplement of the other.
Two angles are said to be adjacent angles when they have a common vertex and a common arm. Also, the non-common arms are on the either side of the common arm. For example, consider the figure below.

Here angle ADB and angle BDC have a common vertex D and a common side DB. Also, their non – common arms DA and DC are on the either side of the common arm DB.
Let us see some examples of adjacent angles.
i) Wall clock
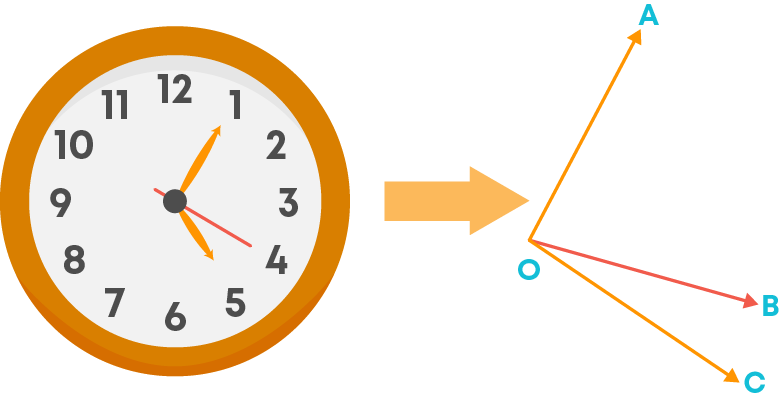
In a wall clock, we can see adjacent angles between the minute hand and the second hand and between the hour hand and the second hand. Both these angles lie next to each other, and they are adjacent angles.
ii) Pizza slice
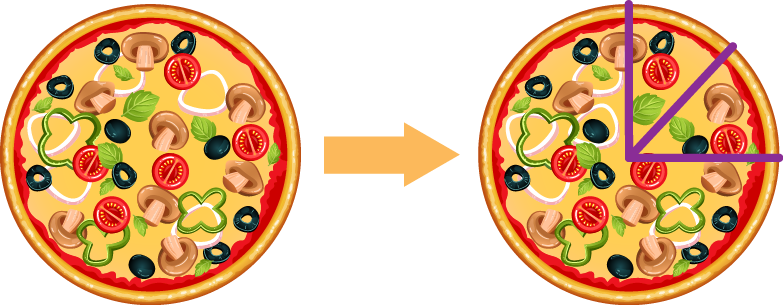
Between the slices of a pizza, we can see adjacent angles.
iii) Between pages of a book

Between the pages of a book, we find a pair of angles, placed next to each other.
Let us now learn about linear pair of angles. Look at the pair of angles given below.
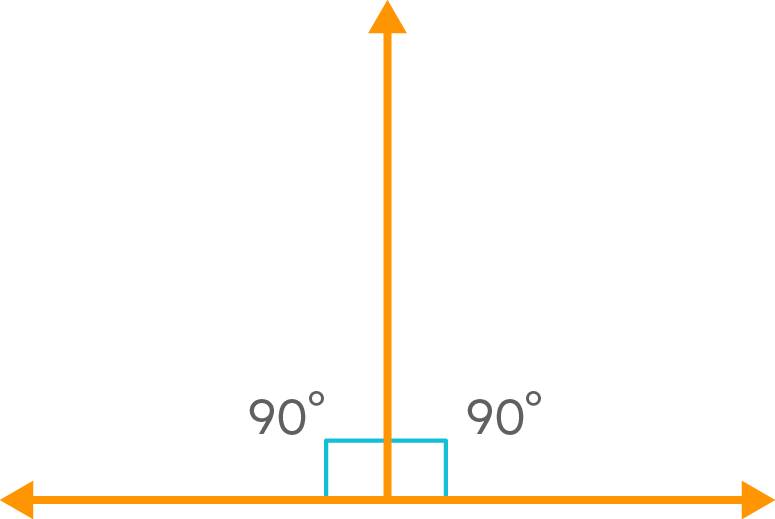
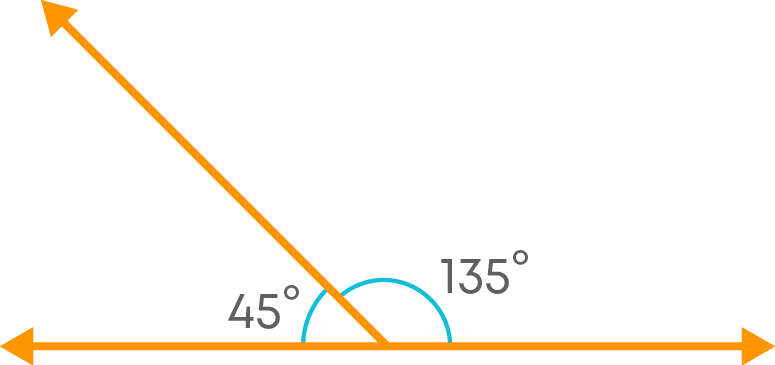

Do these pairs have anything in common? Each pair of angles are adjacent to each other and the sum of the measures of each pair is 180°.
Such pairs of angles are called linear pair of angles. Now, let us define linear pair of angles.
A linear pair of angles are a pair of adjacent angles whose sum is 180°. That is, the angles make a straight line. For example, consider the figure below.
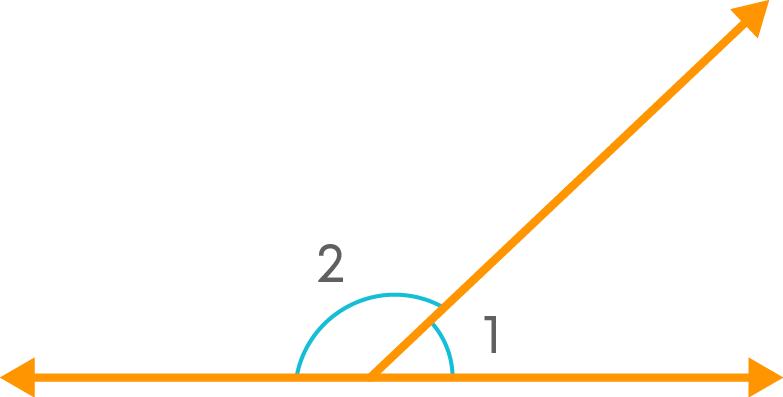
Here the angles 1 and 2 are adjacent. Also, the non-common arms make a straight line. So, we call ∠1 and ∠2 as a linear pair.
In other words, the two angles are linear if the angles are adjacent and supplementary.
Let us see some examples of linear pairs around us.
i) Hands of a clock showing 6’O clock.
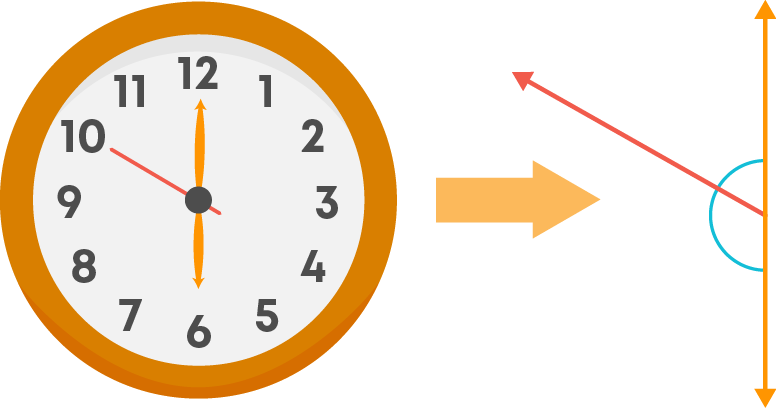
Here is a wall clock showing the time as 6’O clock. We can see the angle between the minute hand and the second hand. Also, there is an angle between the hour hand and the second hand. These angles are adjacent and form a straight line too. So, this represents a linear pair.
ii) Ladder placed against a wall
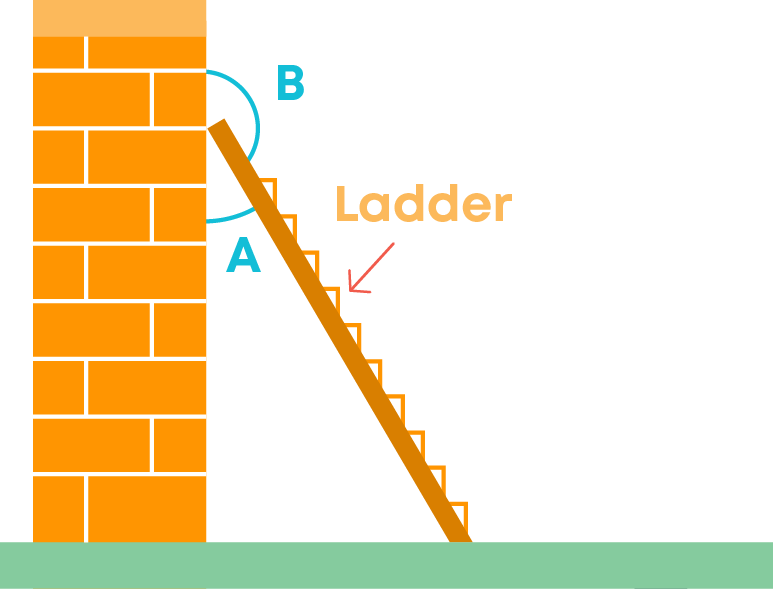
Here two angles are formed against the wall. It represents a linear pair.
iii) Scissor
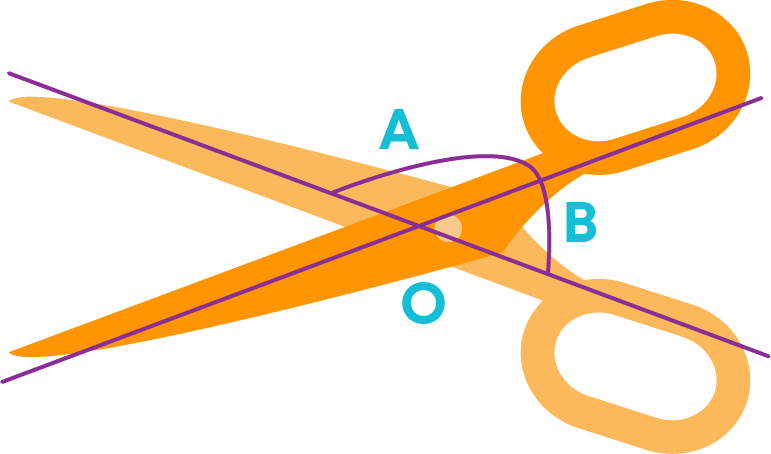
Here we can see that the flanks of the scissors, are adjacent to each other and have a common vertex O, which form an angle of 180 degrees or form a straight line.
Let us take two intersecting lines AB and CD.
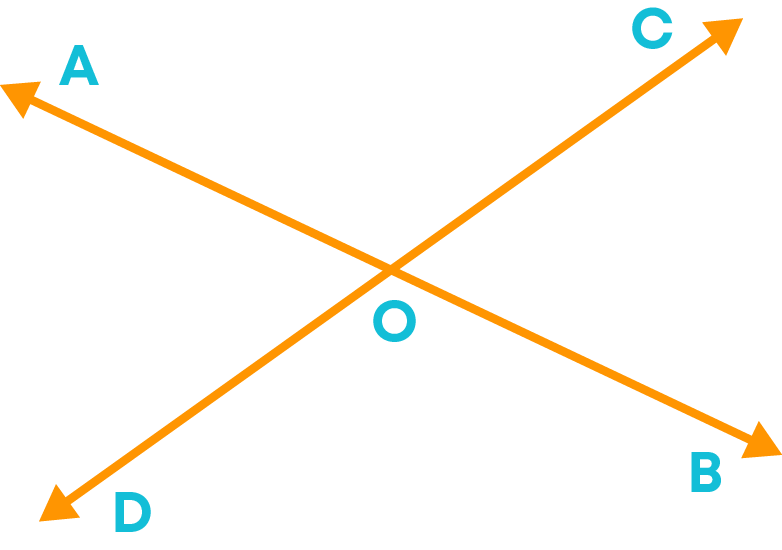
We can see that the two lines AB and CD intersect at the point ‘O’. Did you see the formation of angles between lines? Yes, you can see the four angles which are formed between the two lines.
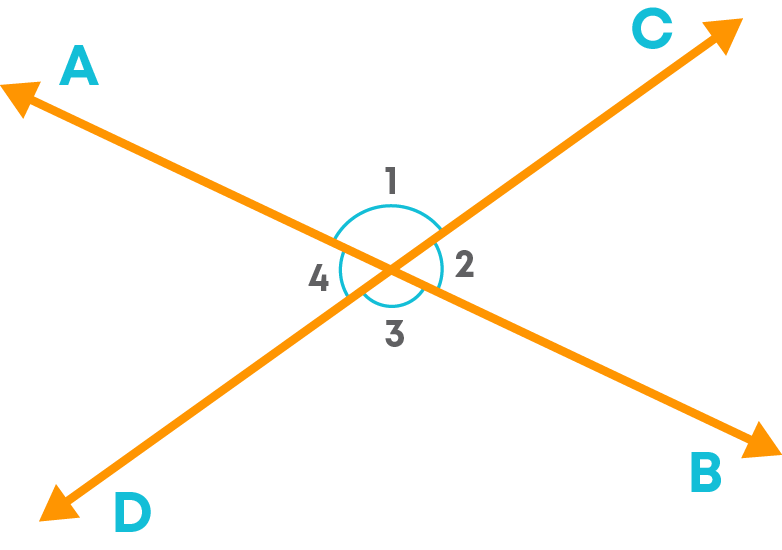
Now, let us learn what vertically opposite angles are.
When two lines intersect each other, the opposite angles are formed due to intersection. These opposite angles are called vertically opposite angles. Here, we say ∠1 is vertically opposite to ∠3 and ∠2 is vertically opposite to ∠4.
∠1 and ∠3 are a pair of vertically opposite angles, and ∠2 and ∠4 are a pair of vertically opposite angles.
When two lines intersect at a point:
- There are pairs of opposite angles formed at the point of intersection.
- Each pair of opposite angles are equal.
Consider the two lines PQ and RS such that the two lines intersect at ‘O’.
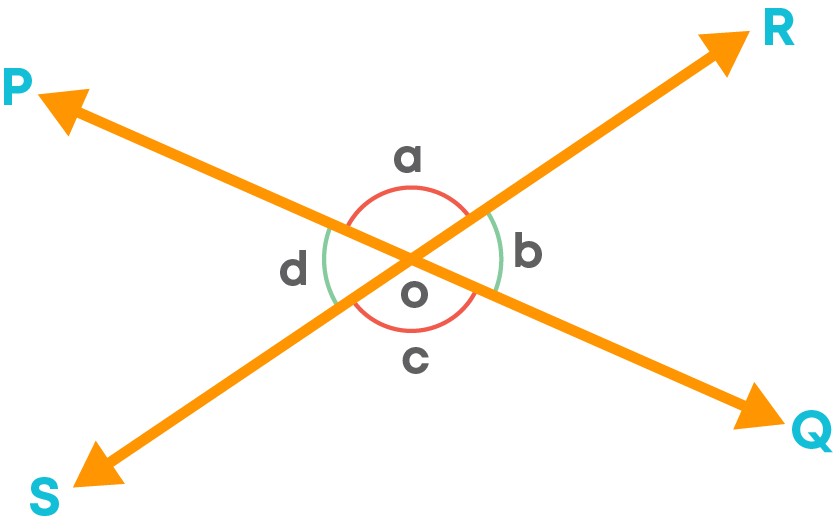
From the figure, we can see that ∠a and ∠b are a linear pair. So, ∠a + ∠b = 180⁰. From this, we can write ∠a = 180 - ∠b.
You can also see that ∠b and ∠c are a linear pair. So, ∠b + ∠c = 180⁰. From this, we can write ∠c = 180 - ∠b.
Therefore, ∠a = ∠c.
So, ∠a and ∠c are a pair of vertically opposite angles.
Pair of Lines
Look at the images below:
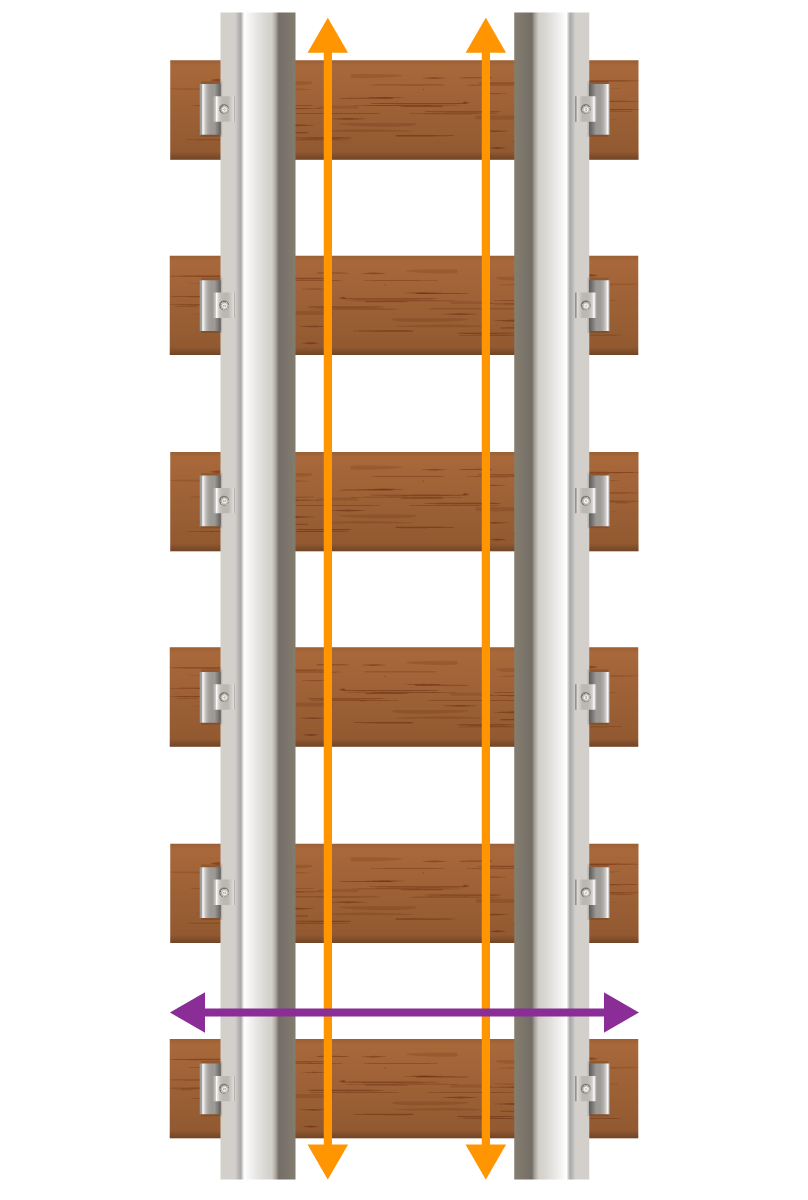

You might have seen a railway line or a stair railing, crossing several other lines. These give an idea of a line passing through a set of lines at distinct points. This intersecting line is a transversal. A line that intersects two or more lines at distinct points is called a transversal. Consider the two lines given below:
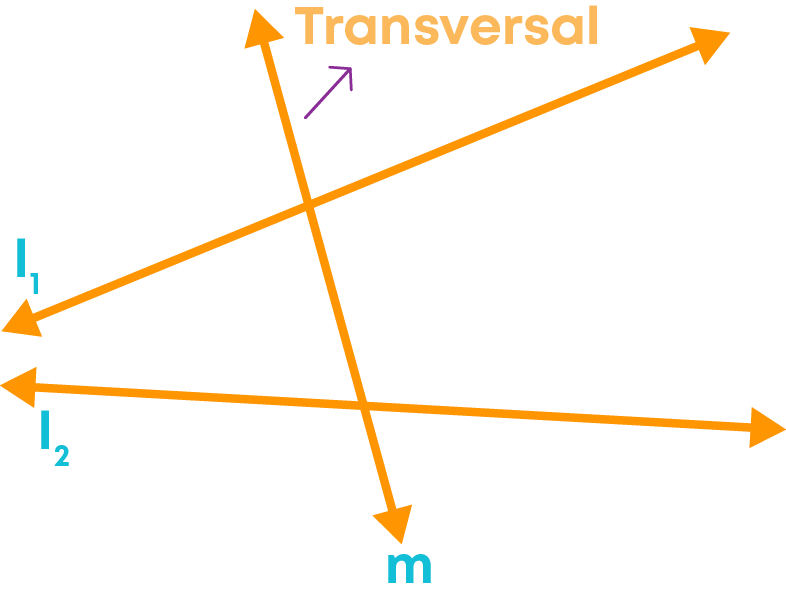
The line ‘m’ is the transversal of the two lines and passes through them at distinct points, A and B.
For the image below, the line ‘p’ is not a transversal, although it cuts the two lines ‘q’ and ‘r’.
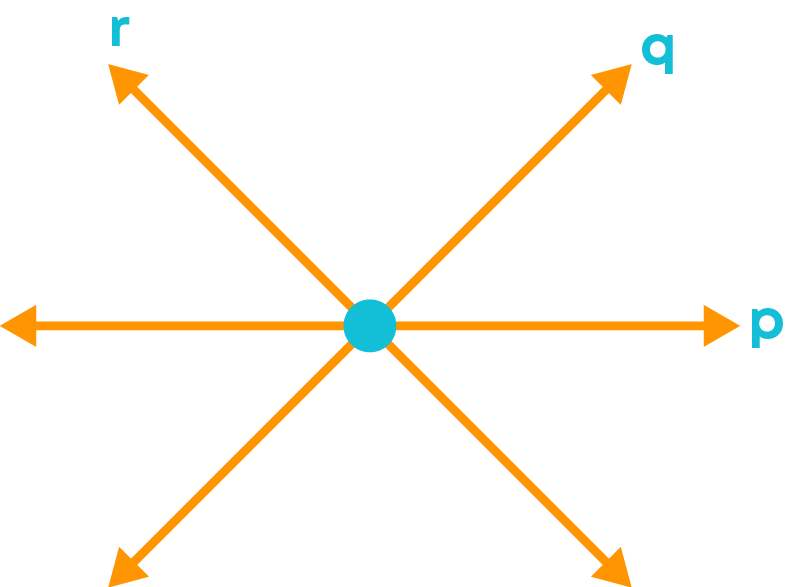
This is because the line ‘p’ does not cut the lines ‘q’ and ‘r’ in two distinct points, in fact, it intersects them at a single point.
Study the table given below:
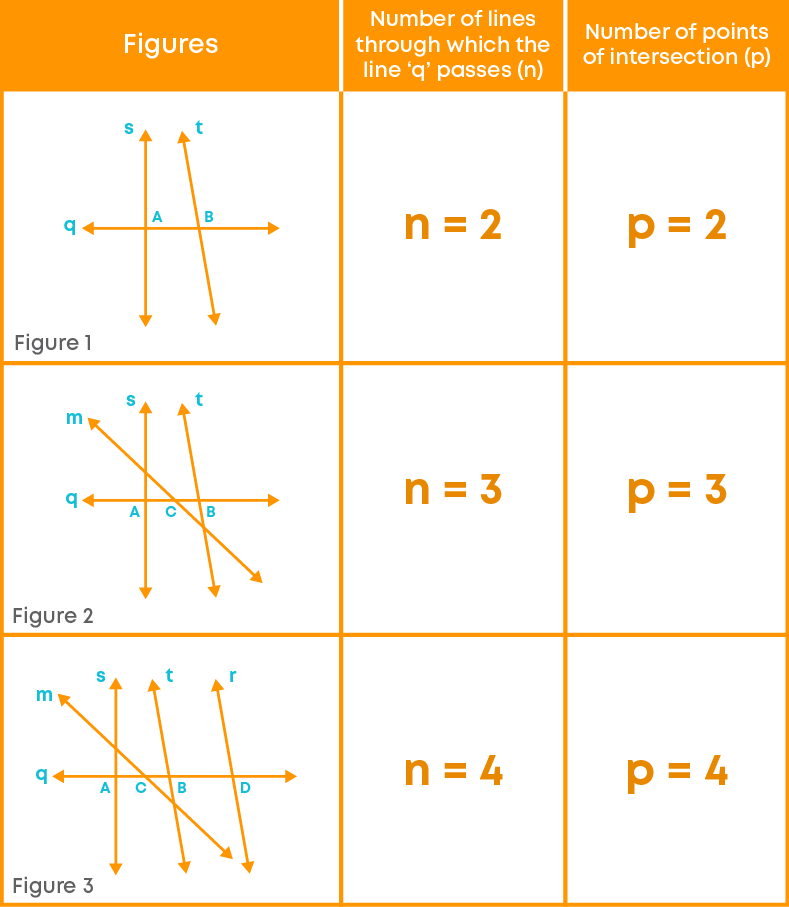
In the given figures, the line ‘q’ is transversal to ‘n’ lines. The line ‘q’ cuts them at ‘p’ distinct points, so the number of points of intersection is ‘p’. Observe that n = p for each figure. Hence, we can say that if a line is a transversal to ‘n’ lines, the number of points of intersection is also ‘n’.
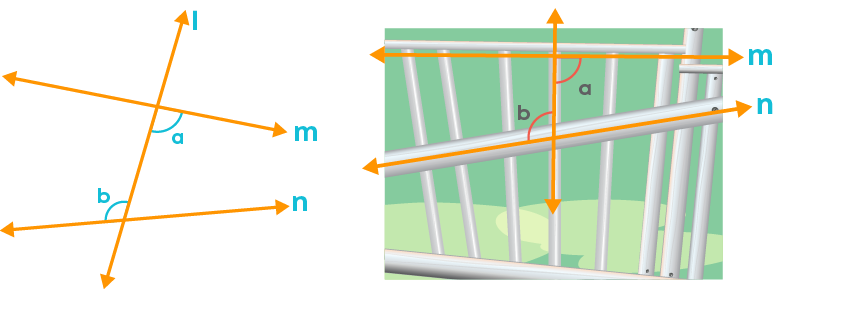
Look at the pair of angles given below:
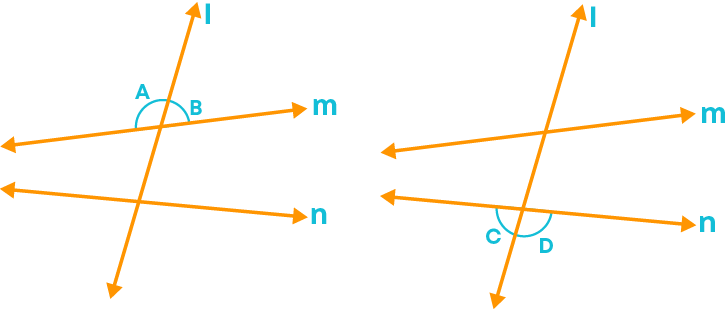
Observe the position of the angles relative to the two lines ‘m’ and ‘n’.
Exterior Angles are formed when a transversal intersects two or more lines. Each pair of these angles are formed on the exterior sides of the lines and lie on both sides of the transversal. For example, we can see the pair of angles at P namely ∠APX, ∠BPX, and at Q namely ∠CQY, ∠DQY.
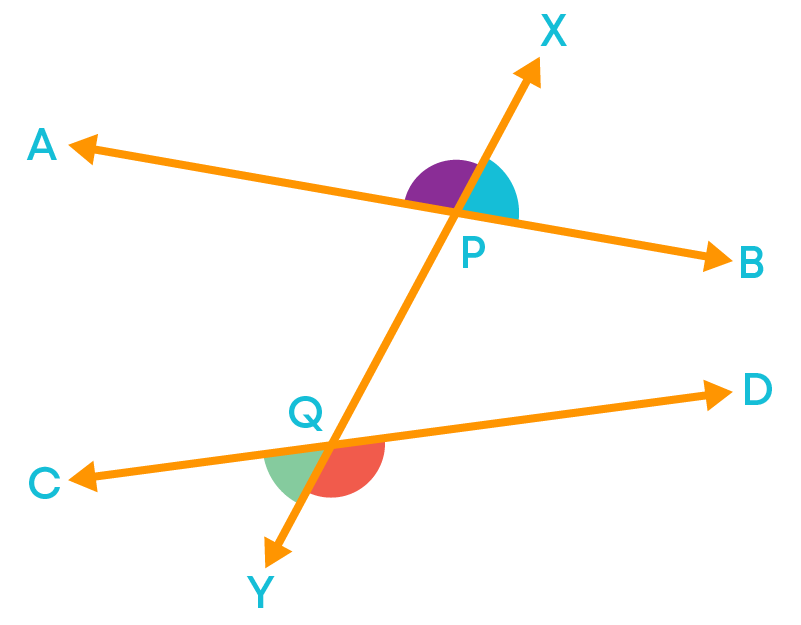
We call these angles at P and Q as exterior angles since each pair of these angles are formed on the exterior sides of the lines and lie on both sides of the transversal.
So, when two lines AB and CD are intersected by a transversal XY, four exterior angles ∠APX, ∠BPX, ∠CQY, and ∠DQY are formed.
Exterior Angles are a pair of angles formed on the exterior sides of the lines and lie on both sides of the transversal.
Look at the pair of angles given below.
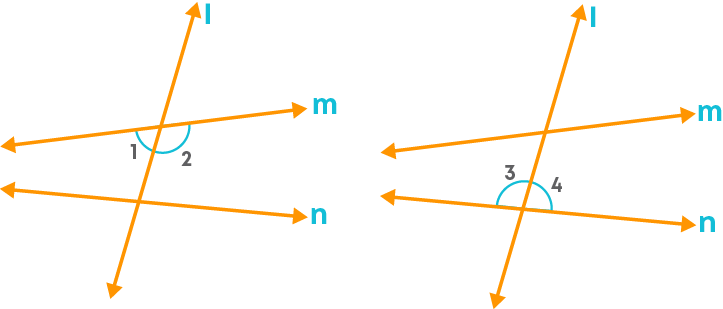
Observe the position of the angles relative to the transversal l.
Interior Angles are formed when a transversal intersects two or more lines. Each pair of these angles are formed on interior sides of the lines and lie on both sides of the transversal. For example, we can see the pair of angles at P namely ∠APQ, ∠BPQ, and at Q namely ∠CQP, ∠DQP.
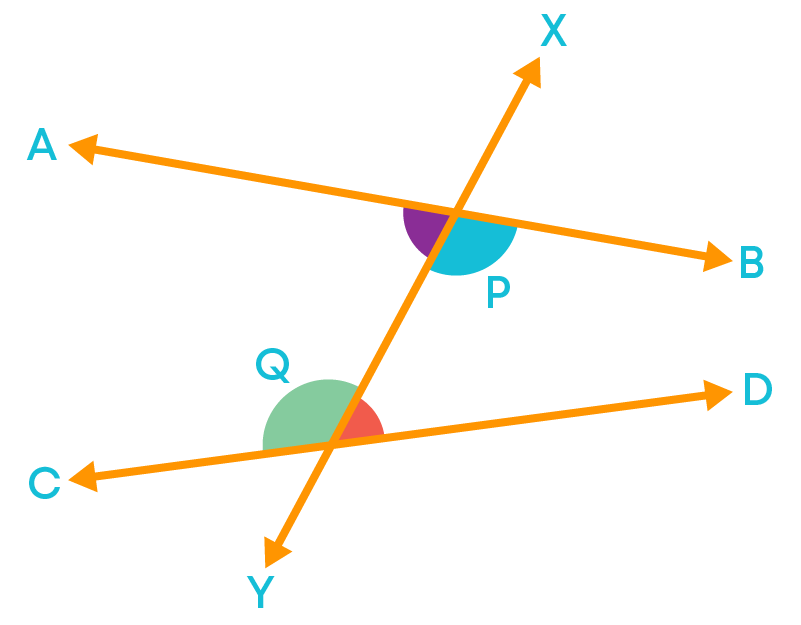
We call the angles at P and Q as interior angles since each pair of these angles are formed on the interior sides of the lines and lie on both sides of the transversal. So, when two lines AB and CD are intersected by a transversal XY, four interior angles ∠APQ, ∠BPQ, ∠CQP, ∠DQP are formed.
Interior Angles are pair of angles formed on interior sides of the lines and lie on both sides of the transversal.
When two lines are intersected by their transversal, four pairs of angles have the same position at each intersection of every two lines. To understand the ‘same position’, let us see the pair of marked angles given below.
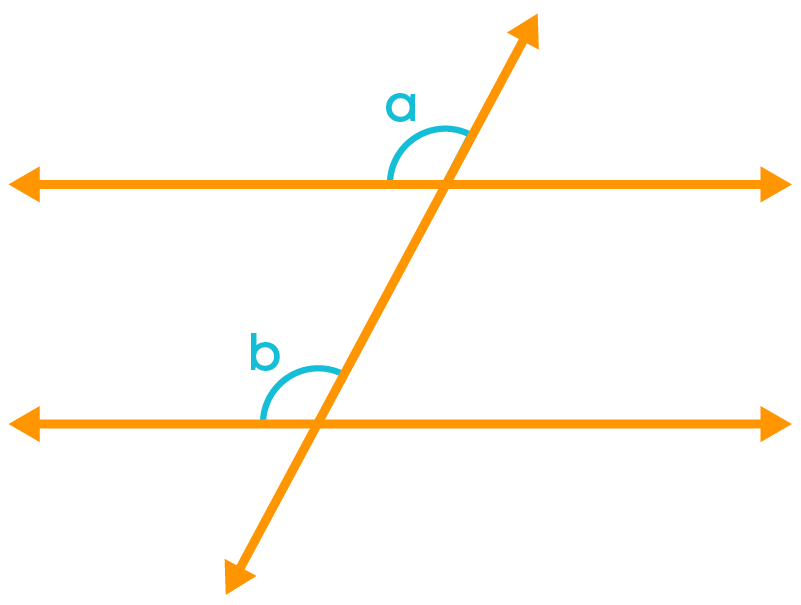

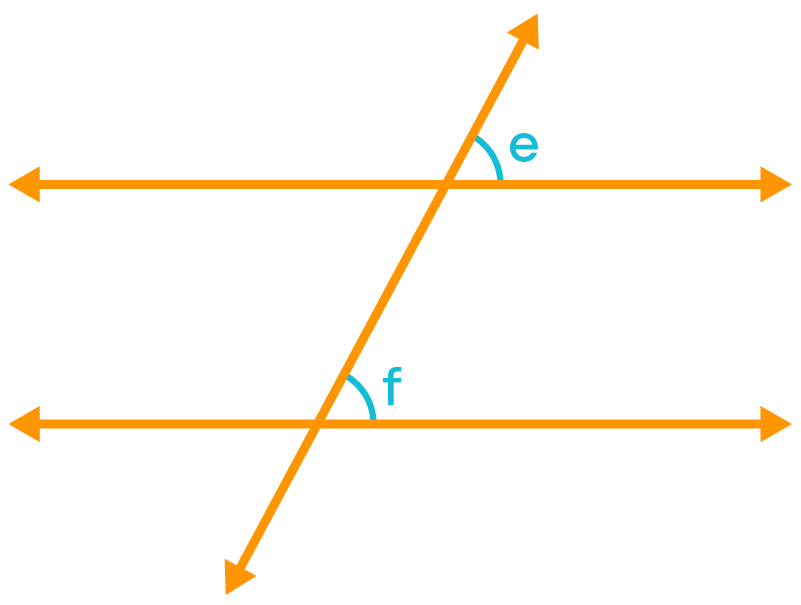
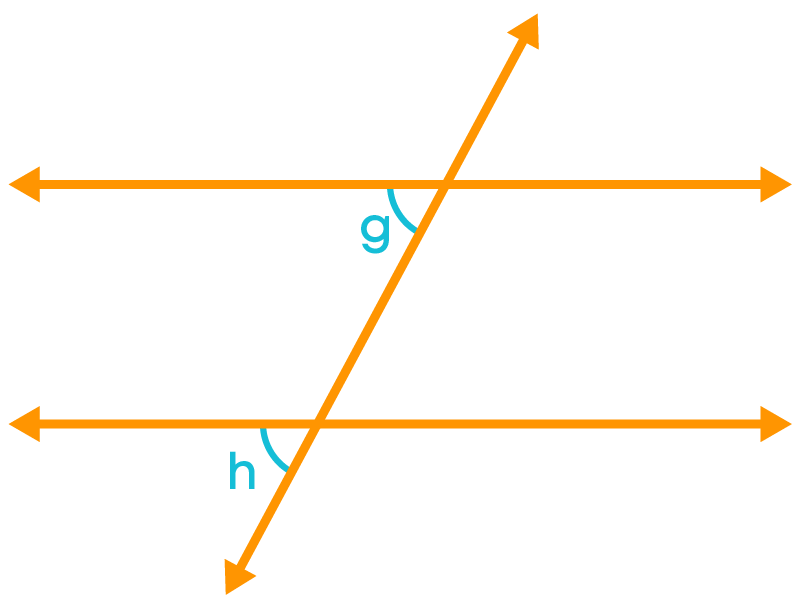
Each pair of such angles are corresponding angles and a total of four pairs of corresponding angles are formed. In each pair of corresponding angles, one angle will be an exterior and the other angle will be an interior angle, each lying on different vertices. They will not be adjacent angles.
So, the corresponding angles:
(i) have different vertices.
(ii) are on the same side of the transversal
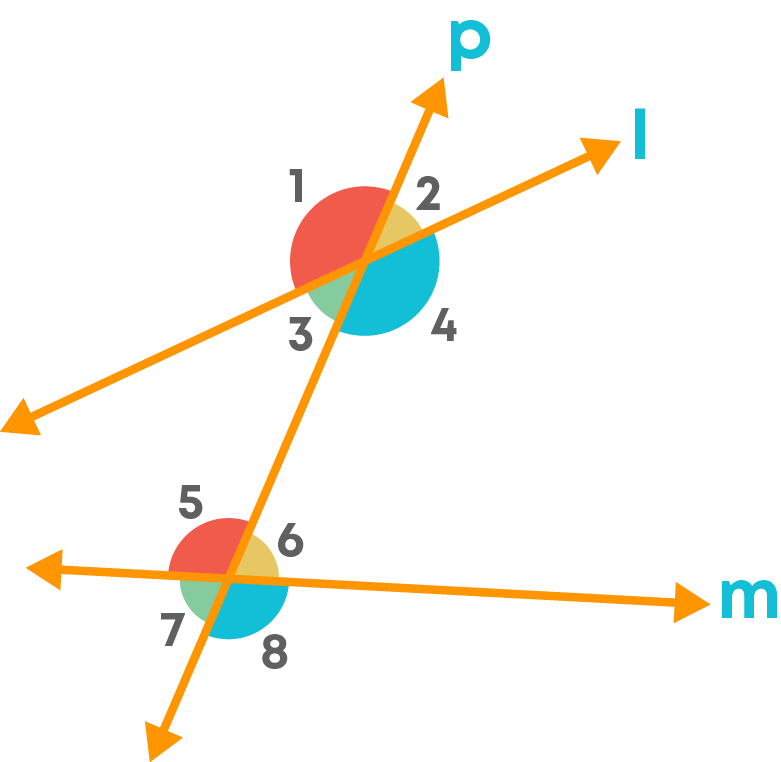
Here, the corresponding pairs are:
∠1 and ∠5
∠2 and ∠6
∠3 and ∠7
∠4 and ∠8
Corresponding angles are pair of angles such that one angle will be an exterior and the other angle will be an interior angle, each lying on different vertices but on the same side of the transversal.
Look at the angles marked in each of the figures given below.
Observe the position of the angles relative to the two lines ‘m’ and ‘n’.
Let us consider the two lines AB and CD intersected by their transversal XY as given in the figure below. Observe that the four interior angles ∠YPA, ∠YPB, ∠XQC, and ∠XQD are formed.
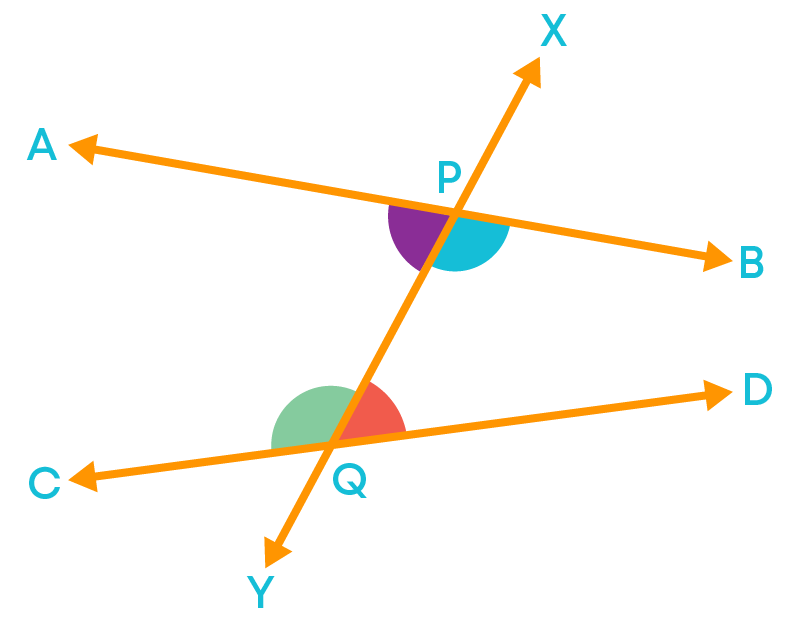
Now, consider the pairs:
- ∠YPA and ∠XQD
- ∠YPB and ∠XQC
For the pairs above, we can see that, angles in the pair are on the alternate sides of the transversal.
Hence, these two pairs of interior angles formed are the alternate interior angles.
So, alternate interior angles:
- are on alternate sides of the transversal and
- lie on the interior sides of the two lines.
When two or more lines are intersected by their transversal, the interior angles which are on the alternate sides of the transversal are called alternate interior angles of the lines and their transversal.
Look at the marked angles given below.
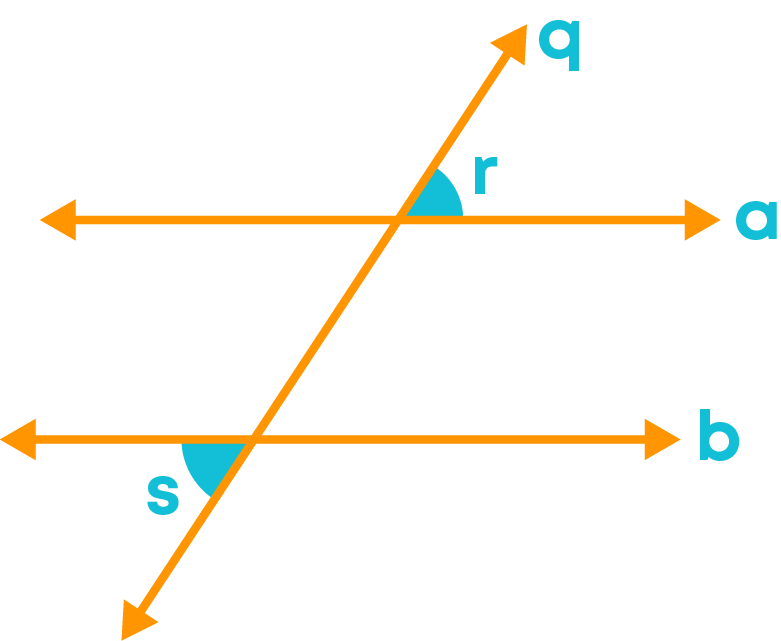
Figure 1: ∠r and ∠s

Figure 2: ∠1 and ∠2, ∠3 and ∠4
Observe the position of the angles relative to the two lines ‘a’ and ‘b’.
Let us consider the two lines AB and CD intersected by their transversal XY as given in the figure below. Observe that the four exterior angles ∠APX, ∠XPB, ∠CQY, and ∠DQY are formed.
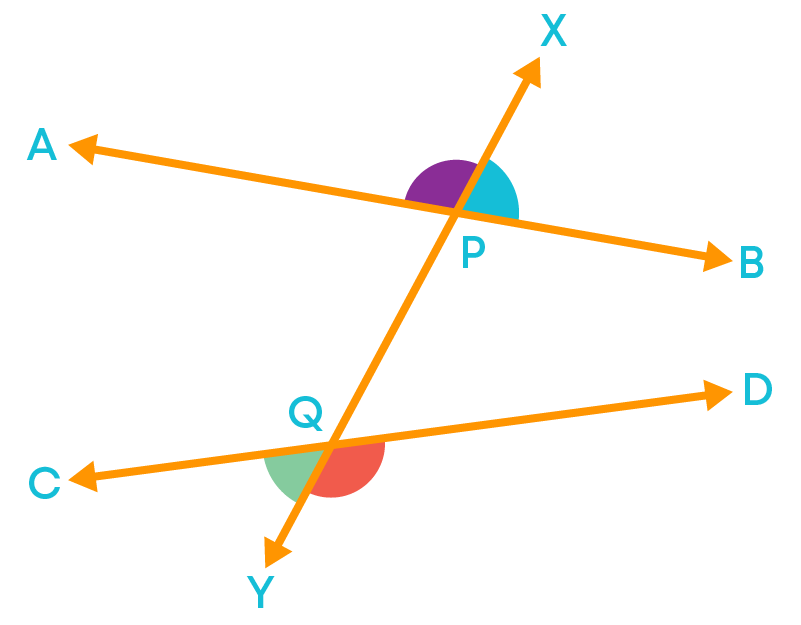
Now, consider the pairs:
- ∠APX and ∠DQY
- ∠XPB and ∠CQY
For the pairs above, we can see that the angles in the pairs are on the alternate sides of the transversal. Hence, these two pairs of exterior angles formed are the alternate exterior angles. So, alternate exterior angles:
i. Are on the alternate sides of the transversal and
ii. Lie on the exterior sides of the two lines.
When two or more lines are intersected by their transversal, the exterior angles which are on the alternate sides of the transversal are called alternate exterior angles of lines and their transversal.
Let us consider four lines AB || EF, ED || CB.
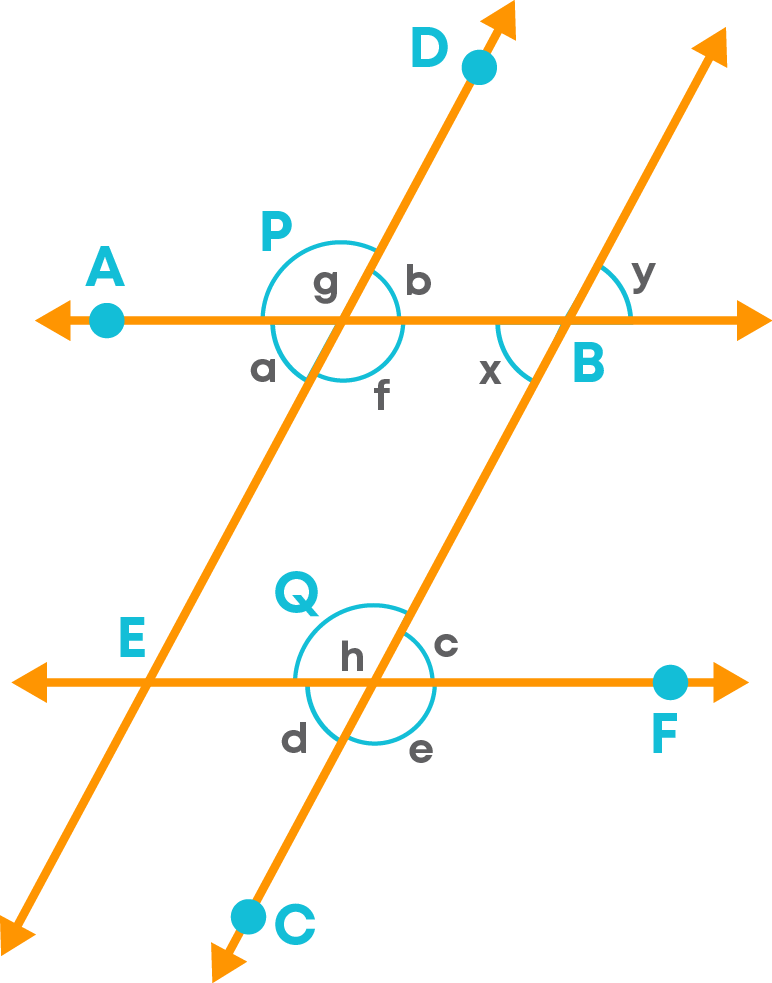
Let us try to identify the different types of angles made by the transversal.
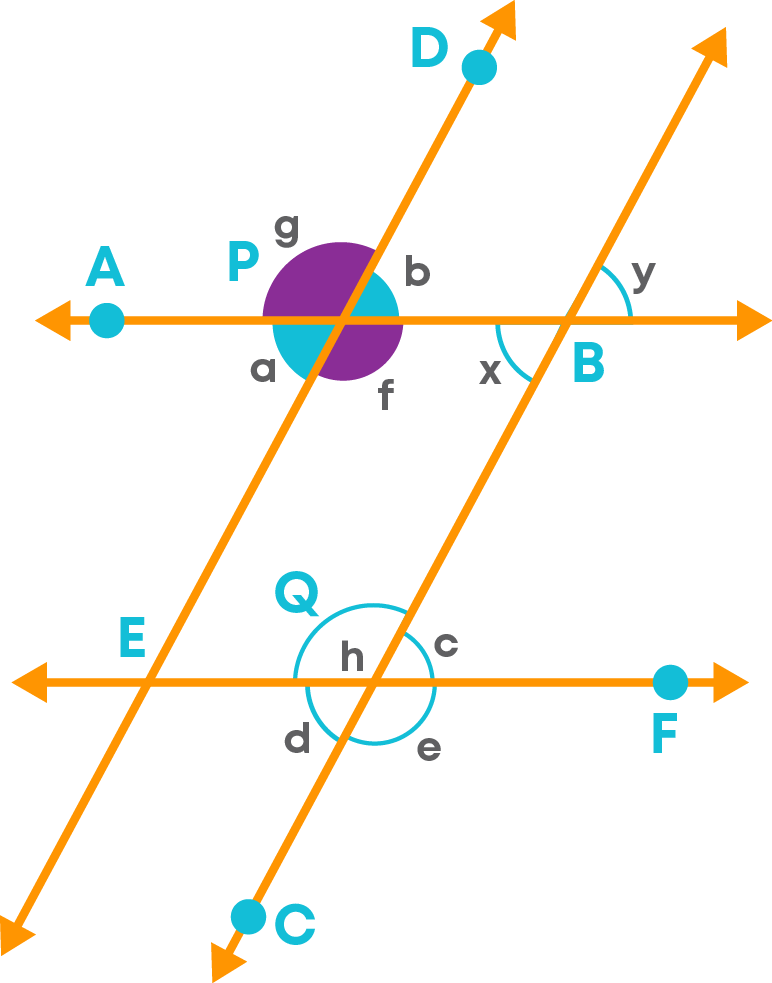
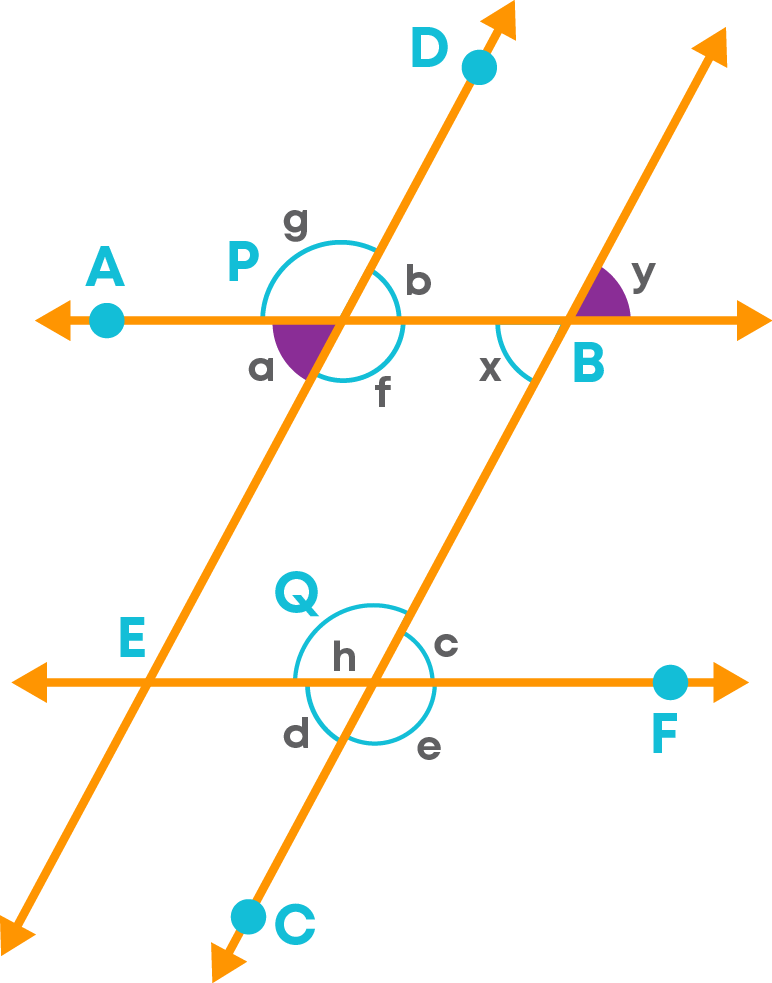
1) Consider AB || EF and line ED as a transversal.
The following pairs of angles
- ∠a and ∠b
- ∠g and ∠f
form vertically opposite angles.
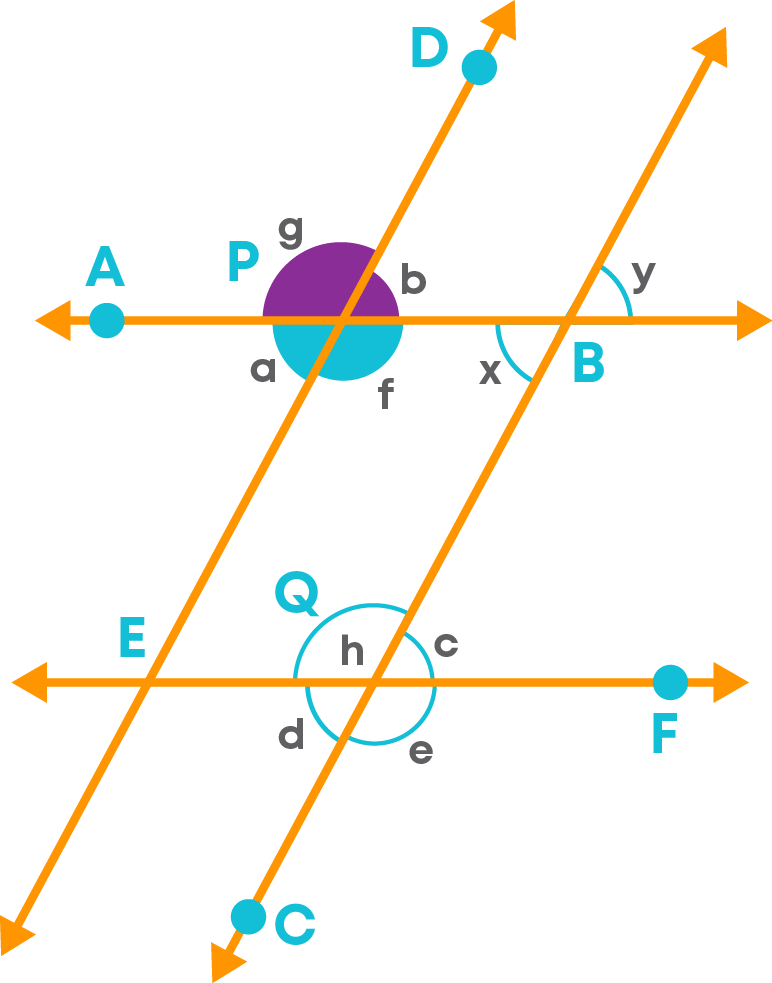
Also, the angles:
- ∠g and ∠b
- ∠a and ∠f
form a linear pair of angles as they form a straight angle, hence, they are supplementary. They are also adjacent angles.
2) Now let us consider AB || EF and line CB as a transversal.
The angles ∠x and ∠c form a pair of alternate interior angles.
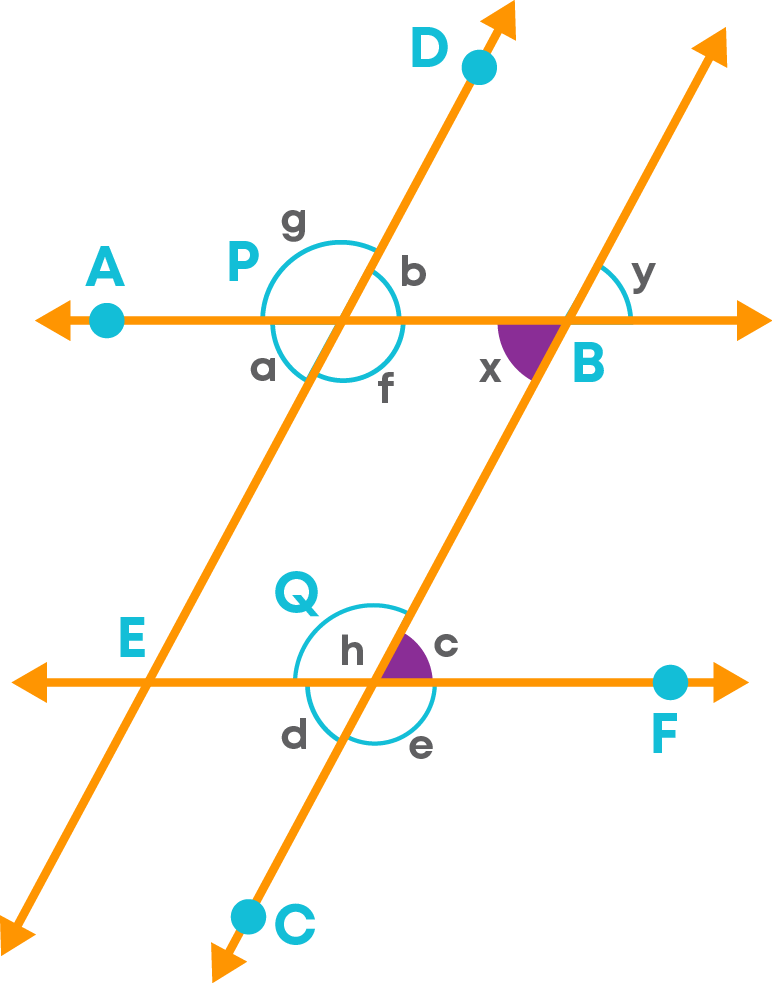
3) Consider ED || CB and line AB as a transversal.
The angles ∠b and ∠y form a pair of corresponding angles.

The angles ∠a and ∠y form a pair of alternate exterior angles.
Transversal to the Parallel Lines
Let us learn about an important property of parallel lines and the corresponding angles formed by the transversal on it. Consider two lines PR || LN. TS is a transversal of these parallel lines.
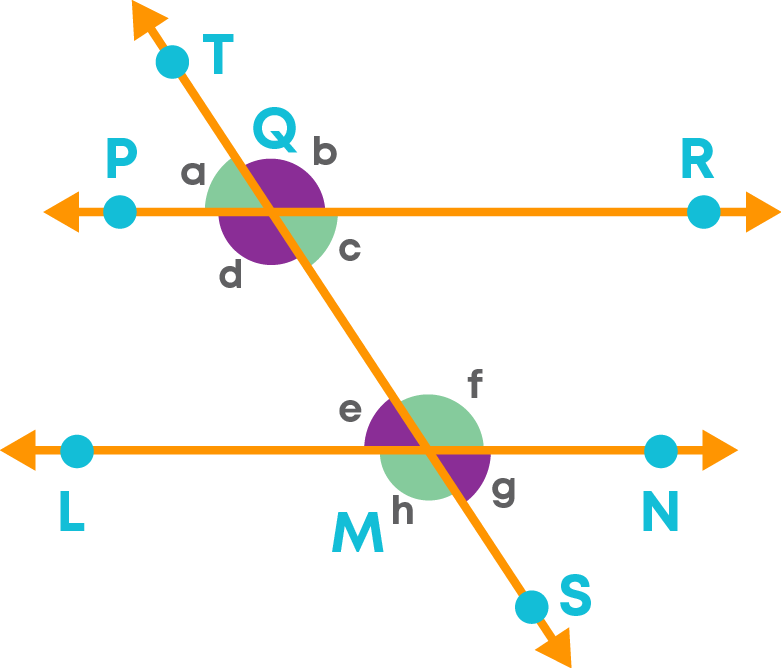
The angles ∠a, ∠b, ∠c, ∠d, ∠e, ∠f, ∠g and ∠h are formed at the points of intersection of the transversal on these parallel lines.
The pair of corresponding angles are given below:
∠a and ∠e
∠d and ∠h
∠b and ∠f
∠c and ∠g
The corresponding angles made by a transversal of parallel lines are equal.
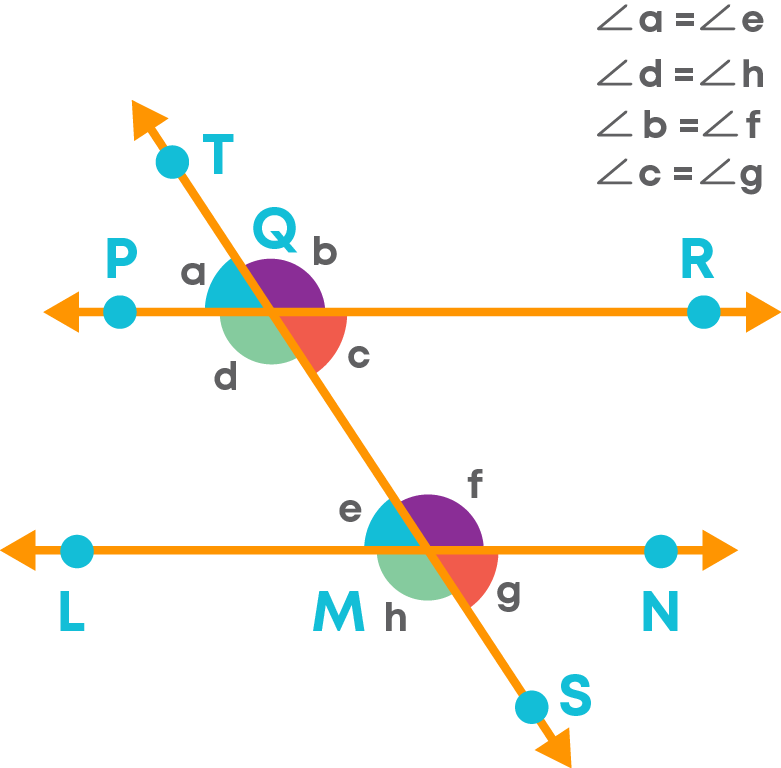
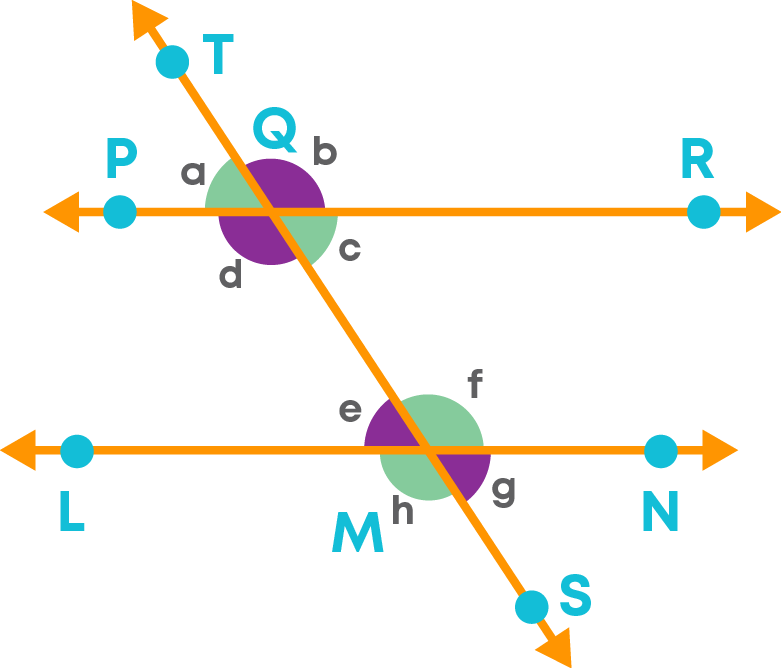
Let us learn about an important property of parallel lines and the alternate interior angles formed by a transversal on it. Consider two lines PR || LN. TS is a transversal of these parallel lines.

The angles ∠a, ∠b, ∠c, ∠d, ∠e, ∠f, ∠g and ∠h are formed at the points of intersection of the transversal on these parallel lines.
The pair of alternate interior angles are given below:
∠d and ∠f, ∠c and ∠e
Each pair of alternate interior angles made by a transversal of parallel lines are equal.
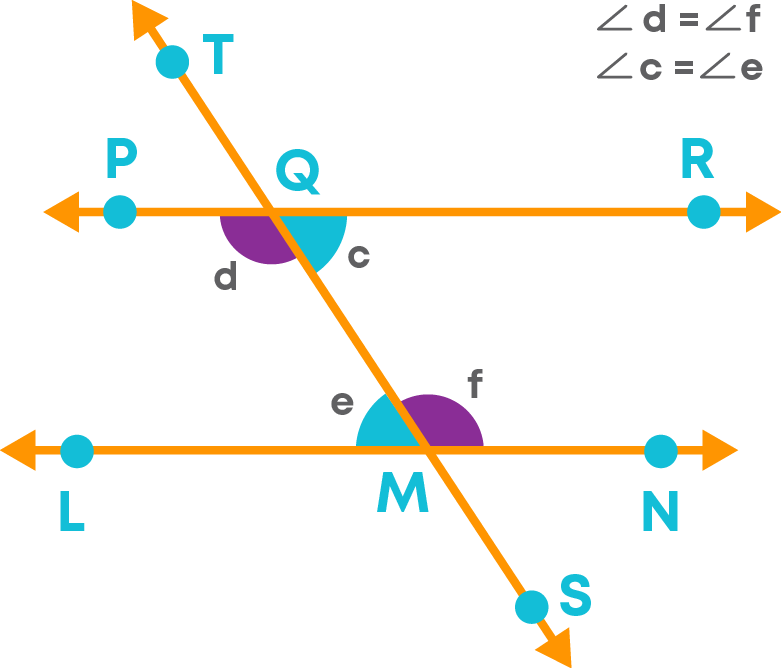
Let us learn about an important property of parallel lines and the interior angles formed by a transversal on it. Consider two lines PR || LN. TS is a transversal of these parallel lines.
The angles ∠a, ∠b, ∠c, ∠d, ∠e, ∠f, ∠g and ∠h are formed at the points of intersection of the transversal on these parallel lines.
Angles ∠d and ∠e lie on the same side of the transversal.
Angles ∠c and ∠f lie on the same side but opposite to the angles ∠d and ∠e.
The interior angles on the same side of a transversal are supplementary.
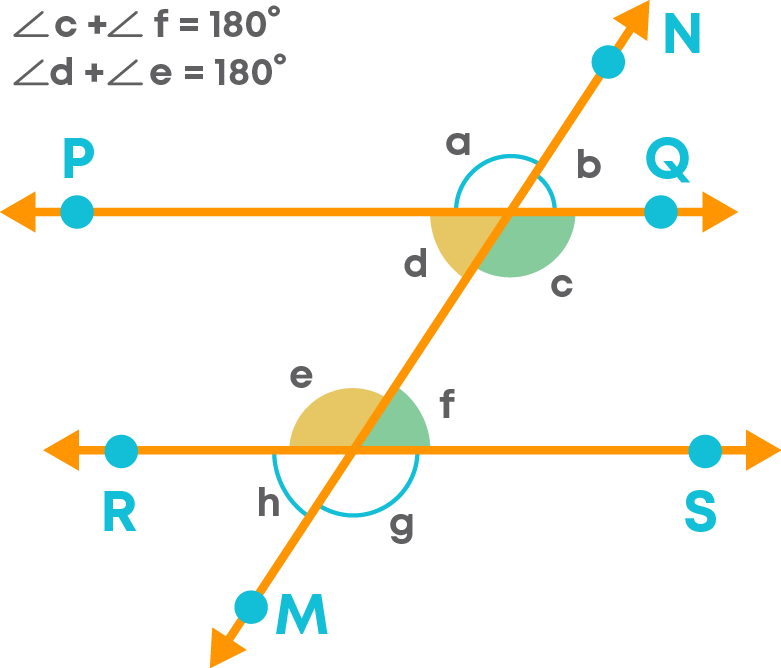
We can check whether the given two lines are parallel or not by the following conditions:
- Check whether the pairs of corresponding angles are equal or not.
- Check whether the pairs of alternate interior angles are equal or not.
- Check whether the pairs of interior angles on the same side of the transversal are supplementary or not.
If anyone of the condition holds, then the given lines must be parallel.
Common Errors
The following are topics in which students make common mistakes when dealing with lines and angles:
- 1. Complementary angles are not the same as supplementary angles
- 2. Vertically opposite angles are not formed only for two intersecting lines but are also formed when a transversal cuts a number of lines
- 3. Identifying a transversal when a set of lines are given
Complementary Angles Are Not The Same As Supplementary Angles
Remember!
For two angles to be complementary, their sum should be 90°. For example, here we can see the angles 40° and 50°. The sum of these angles is 180°.
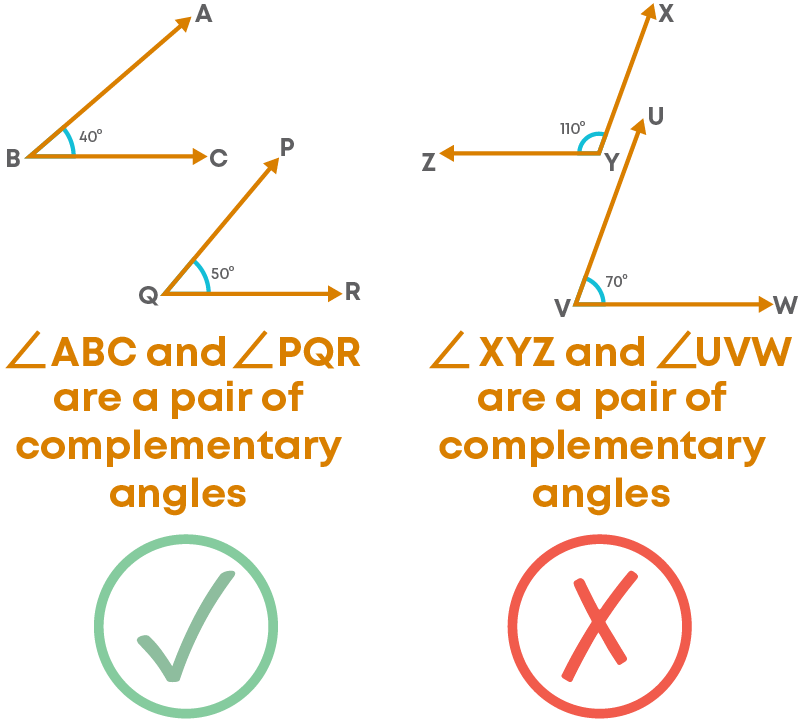
Remember!
For two angles to be supplementary, their sum should be 180°. For example, let us see the pair of angles 130° and 50°. The sum of these angles is 180°.
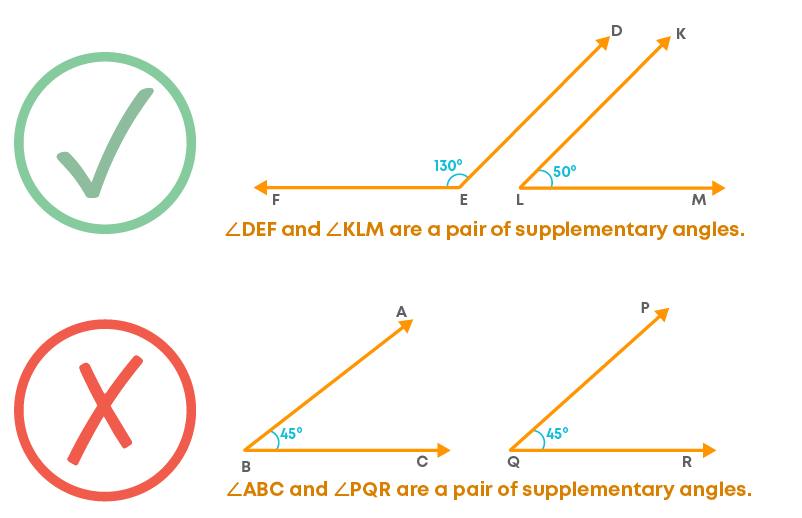
Vertically Opposite Angles Are Not Formed Only For Two Intersecting Lines But Are Also Formed When A Transversal Cuts A Number Of Lines
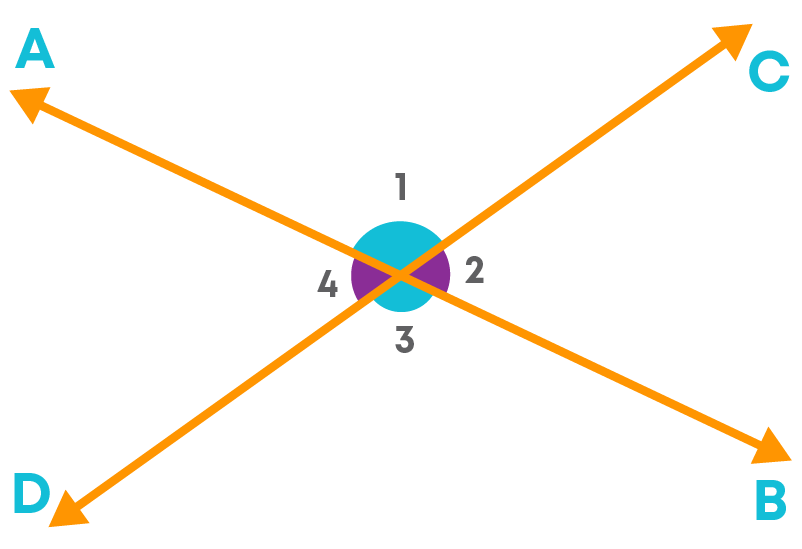
Here, ∠1 and ∠3 are a pair of vertically opposite angles. Similarly, ∠2 and ∠4 are a pair of vertically opposite angles.
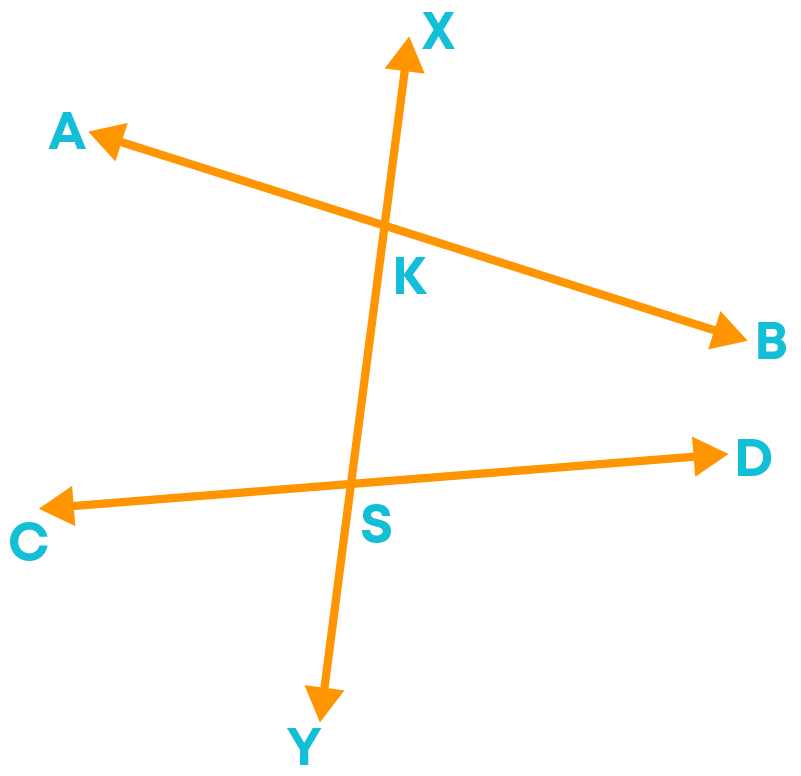
Here,
- (i) ∠AKX and ∠SKB
- (ii) ∠AKS and ∠XKB
- (iii) ∠CSY and ∠KSD
- (iv) ∠CSK and ∠DSY
are a pair of vertically opposite angles.
Identifying A Transversal When A Set Of Lines Are Given
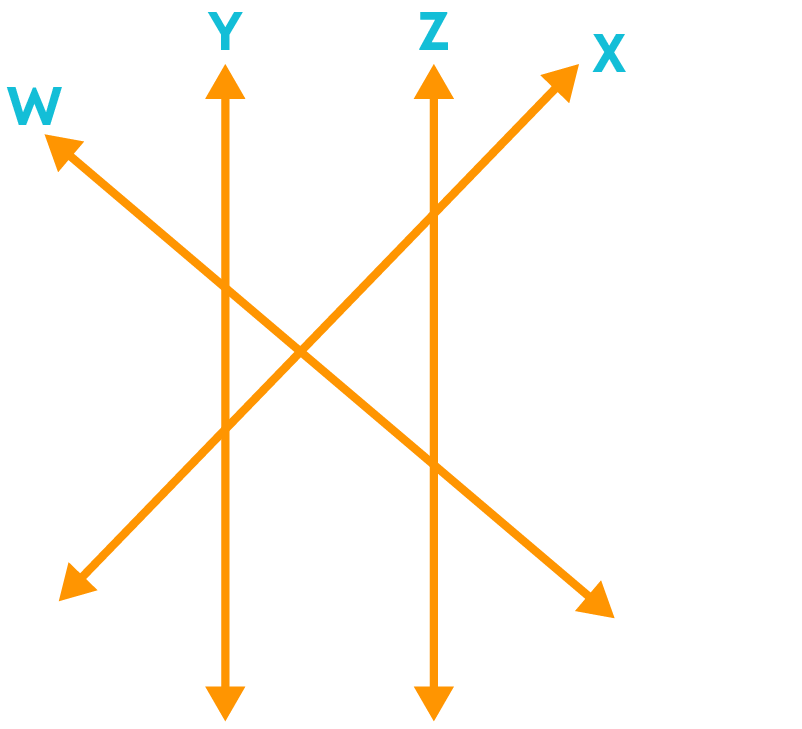
Is line ‘y’ transversal to the lines ‘w’, ‘x’ and ‘z’? No!
A line that intersects two or more lines at distinct points is called a transversal. According to this, line 'y’ should intersect three lines ‘x’, ‘z’ and ‘z’ at three distinct points. But line ‘y’ intersects only lines ‘w’ and ‘x’ but not ‘z’, so it is not a transversal.
So, line ‘x’ is transversal to the lines ‘w’, ‘y’ and ‘z’. Also, line ‘w’ is transversal to the lines ‘x’, ‘y’ and ‘z’.
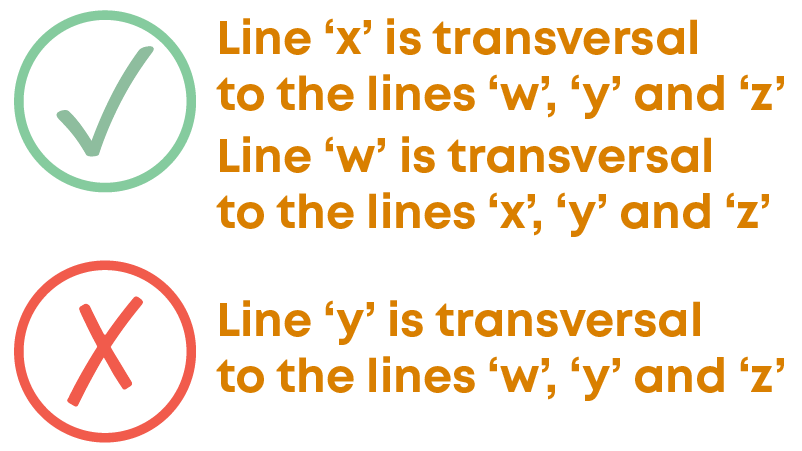
Conclusion
Can you solve the riddle below after reading all about lines and angles?
Amita challenges her friend to find two angles which are supplementary and equal. Help her friend find the measure of these angles.




















































