Introduction
There are many objects around us which are triangular in shape. What are the special properties of this shape and why do we need to learn about them? Let us watch this video to know.
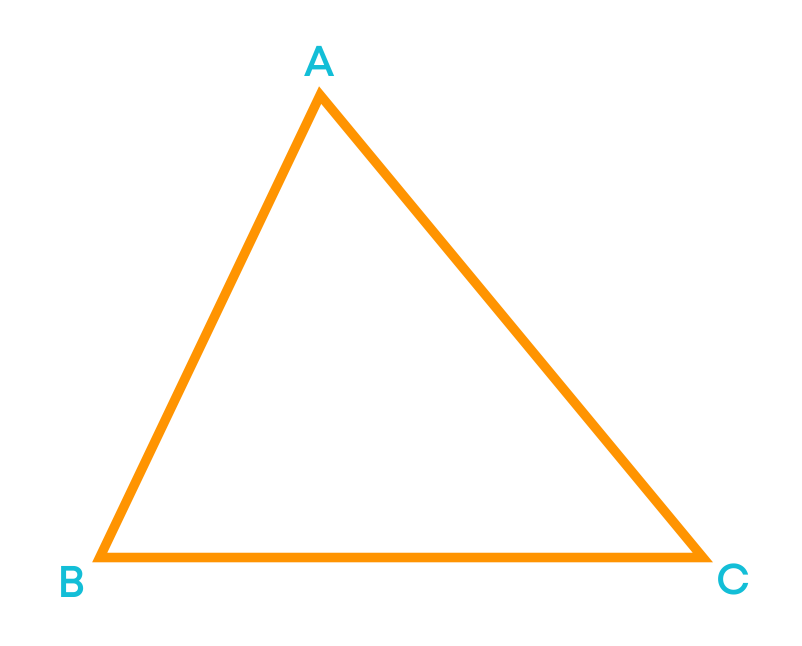
A triangle is a polygon having three sides, three angles and three vertices. For example,

Here ABC is a triangle with sides AB, BC, and CA.
Concepts
The chapter ‘Triangle and its Properties’ covers the following concepts:
Medians and Altitudes of a Triangle
Consider the triangle ABC
Let us bisect the side BC into two equal parts. The point ‘P’ divides BC into two equal parts.

Now, P is the midpoint of the side BC. Let us join the midpoint of BC to its opposite vertex A.

Here the line segment AP, joining the mid-point of BC to its opposite vertex A is called the median of the triangle. Can you find other medians of the triangle by considering the sides AB and AC? We can also draw medians to the sides AB and AC.

opposite side AB.

BR is a median of the triangle ABC. Since BR is a line segment joining vertex B to the midpoint of its opposite side AC.
The line segment joining the vertex of a triangle to the midpoint of its opposite side is called as the median of the triangle.
We know that a triangle has 3 vertices, and we can draw medians from each vertex. The three medians of a triangle are shown below.
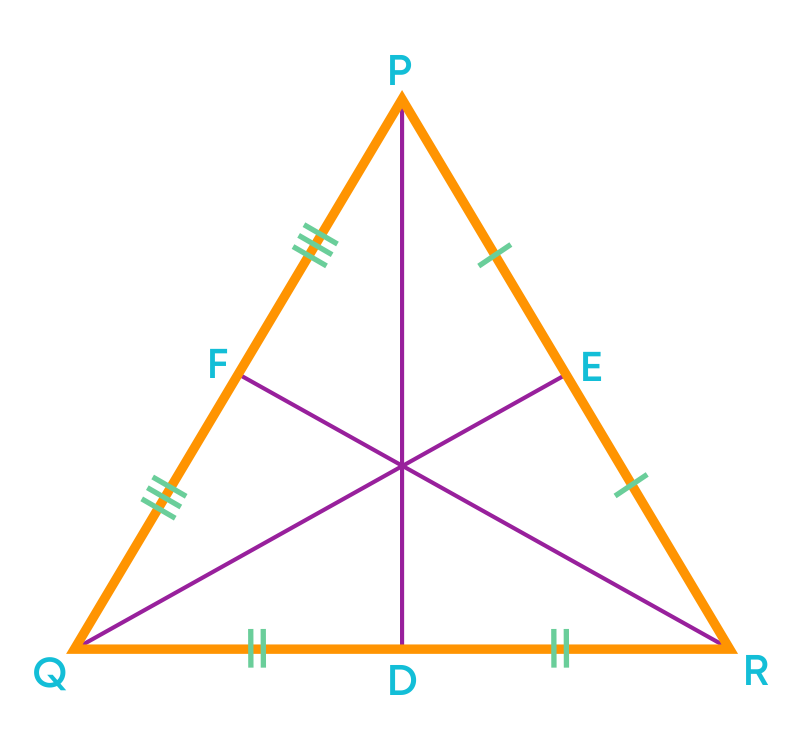
PD, QE, and RF are the three medians in ∆PQR.
In an equilateral triangle, all the medians are of equal length. In an isosceles triangle, two medians drawn from the vertices of the equal angles are equal in length. In a scalene triangle, medians are not equal in measure.
Remember, the medians are always inside the triangle. Consider the acute, obtuse and right-angled triangles and the medians for these triangles.
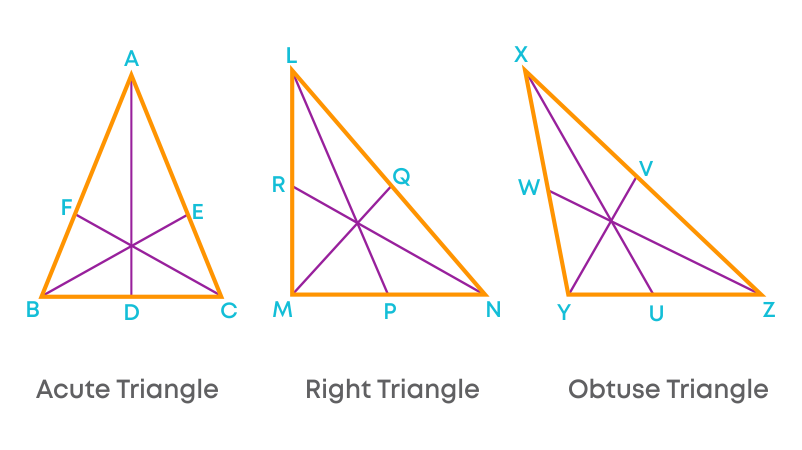
We can see that the medians lie inside the triangles for all these different triangles also.
Consider the following question:
KM is the median of the ∆ KLN and the length of MN is 5 cm. Find the length of side LN.
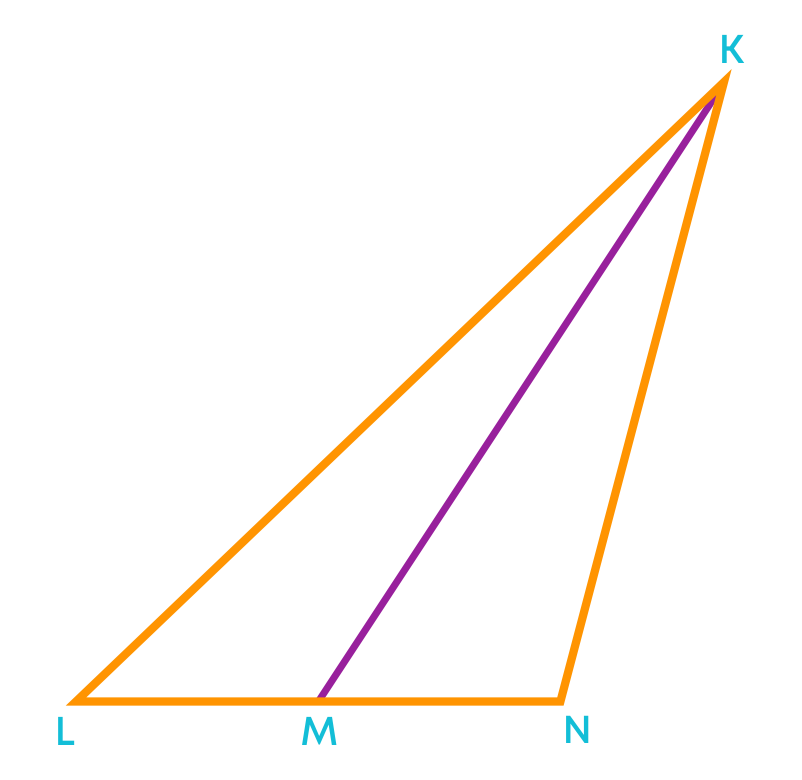
In the given figure, KM is the median of ∆KLN, and MN = 5 cm. Since KM is the median, it will bisect the side LN of ∆KLN. So, LM = MN = 5 cm. Hence, LN = LM + MN = 5 + 5 = 10 cm, or LN = 2 × 5 = 10 cm.
Now, let us learn how to construct a median. Consider the triangle ABC.
Construct the perpendicular bisector to the side AC using a compass to obtain the midpoint of AC. Now, we get the midpoint of AC.

Draw a segment from that midpoint to the opposite vertex, i.e., we draw the line segment from D to B.
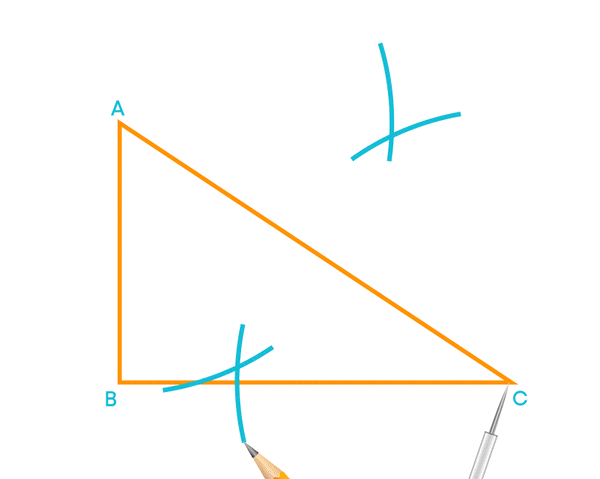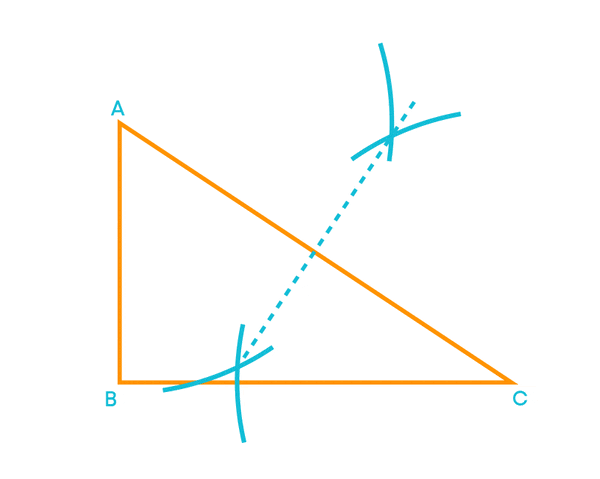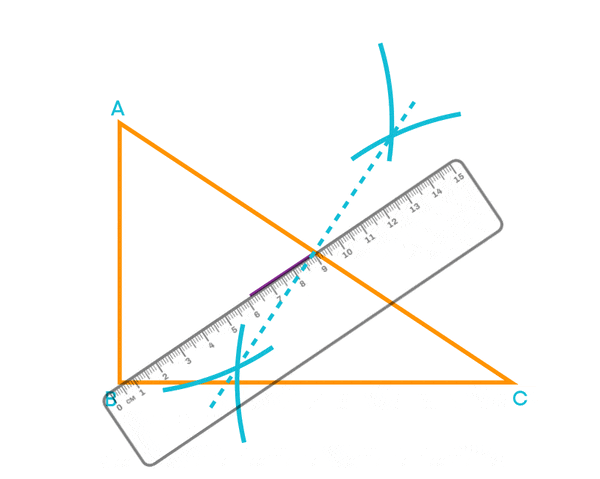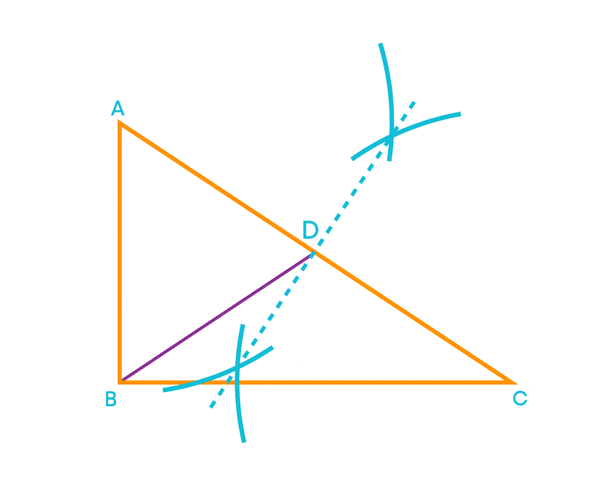
The line segment BD is the median of the triangle.
- Do the same procedure for the other two sides.

BD, CE, and AF are the medians of the triangle ABC.
Now consider the triangle ABC:
We can draw many line segments from the vertex A to line segment BC.

Now, out of these line segments AD, AE, AF and AG, the line segment AE is perpendicular to the line segment BC.

We call the line segment AE as the height of the triangle.
- Height of a triangle is the line segment that starts from the vertex, comes straight down to the opposite side of the vertex and is perpendicular to the opposite side.
Height of the triangle is also known as the altitude of the triangle.

In other words, the perpendicular line segment from a vertex of a triangle to its opposite side is the altitude of the triangle. So, AE is the altitude of the triangle ABC. Can you find other altitudes of the triangle? We can also draw altitudes to the sides AB and AC.

BD is the altitude of the triangle ABC as BD is the perpendicular line segment from the vertex B to its opposite side AC.

CF is an altitude of the triangle ABC as CF is the perpendicular line segment from the vertex C of the triangle to its opposite side AB.
The perpendicular line segment from a vertex of a triangle to its opposite side is called an altitude of the triangle.
We know that a triangle has 3 vertices, and we can draw altitudes from each vertex. The three altitudes of a triangle are shown below.
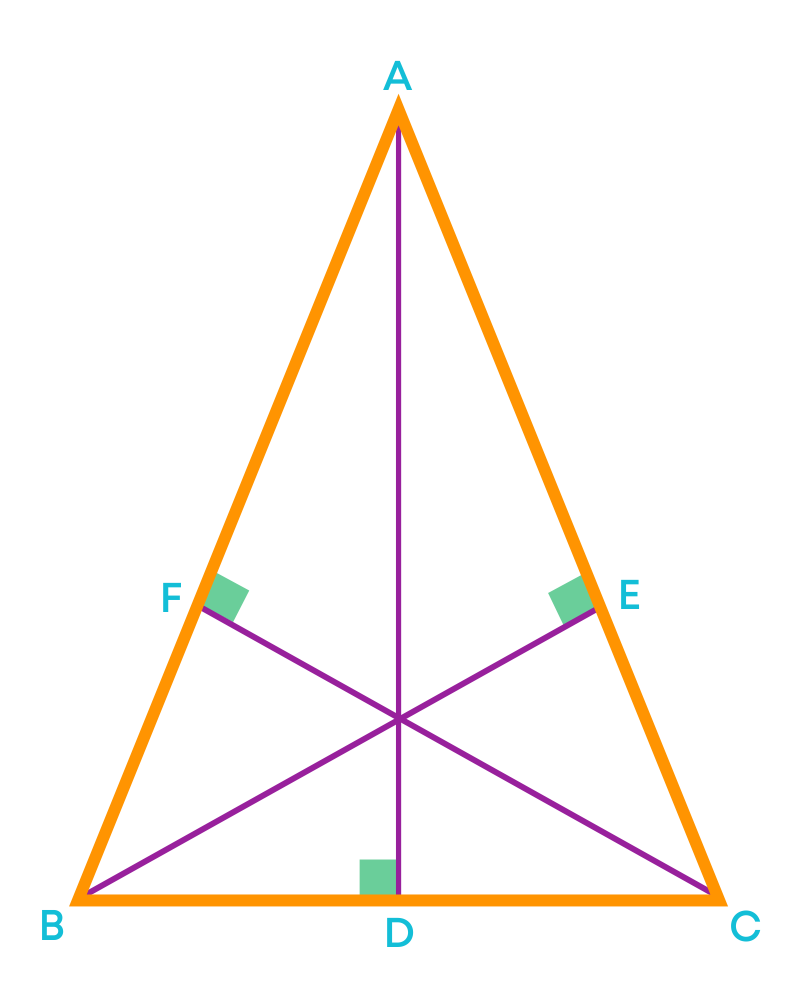
AD, BE, and CF are the three altitudes in ∆ABC.
Consider the acute- angled triangles below and observe the altitudes for the triangles.
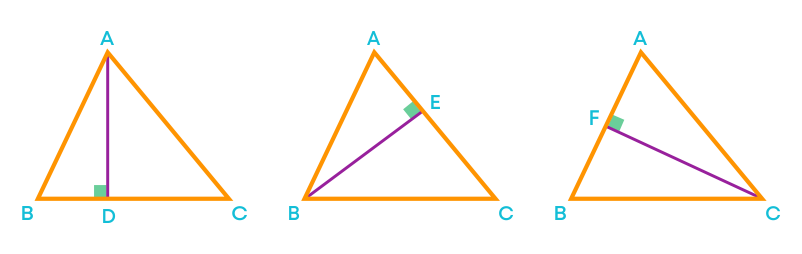
AD, BE, and CF are the three altitudes in ∆ABC.
We can see that for acute-angled triangles the altitudes lie inside the triangles. Now, consider the obtuse- angled triangles below and observe the altitudes for the triangles
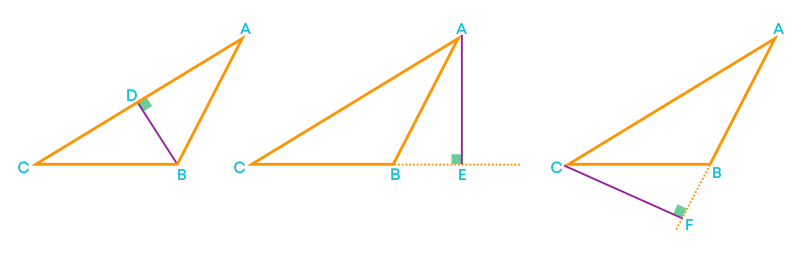
- Here, we can see that for obtuse – angled triangles, the altitudes can lie outside the triangle also.
Let us consider a right-angled triangle and draw the altitudes.
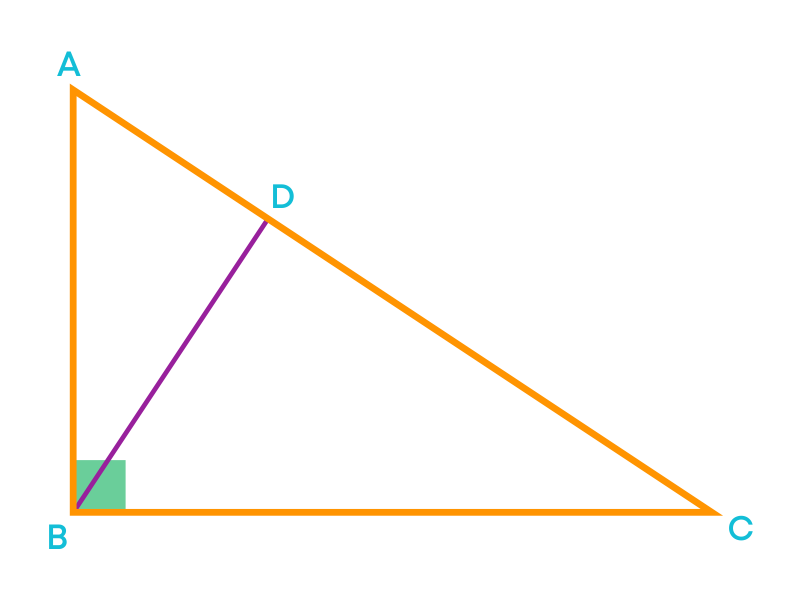
We can draw the altitude from the vertex B as shown in the figure. What about the vertices A and C? In a right-angled triangle, one side is perpendicular to the other side. Here, the two sides AB and BC are perpendicular to each other.
- Altitudes lie inside for an acute-angled triangle.
- One altitude lies inside, and two altitudes are two of its sides for a right-angled triangle.
- Altitudes and medians are the same for an equilateral triangle. In an equilateral triangle, all the altitudes are of equal length.
- In an isosceles triangle, two altitudes drawn from the vertices of the equal angles are equal in length.
- In a scalene triangle, the altitudes are not equal in measure.
Consider the question:
AE is an altitude of ∆ABC and the length of AE is 6 cm. What is the height of ∆ABC?
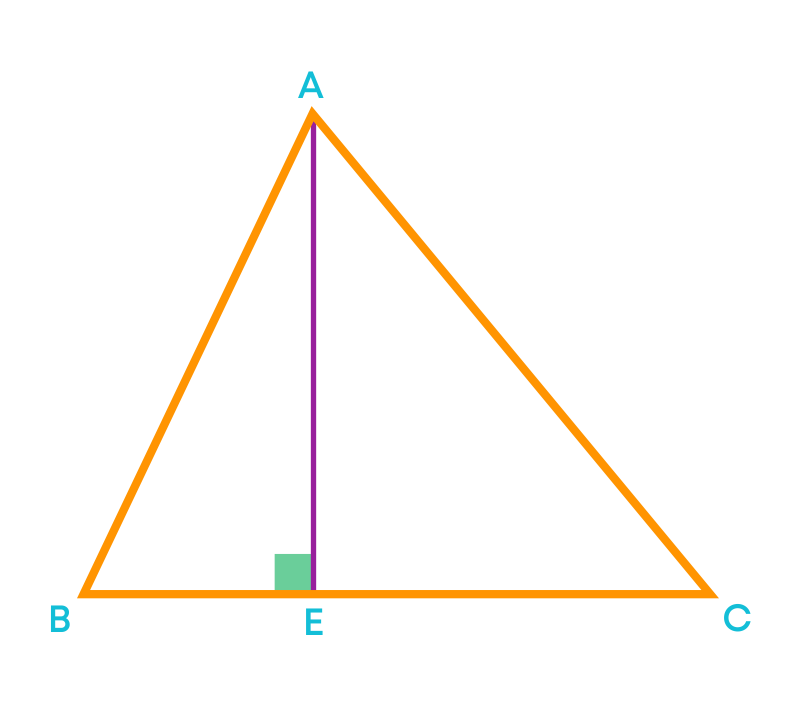
In the given figure, AE is the altitude of ∆ABC. Given that, AE = 6 cm. We know that the altitude of a triangle is nothing but the height of the triangle. So, the height of the ∆ABC is 6 cm.
Now, let us construct the altitudes for the given triangle ABC:

Now, let us draw an altitude from the vertex B.
- Extend the side AC
- Construct a perpendicular line segment from point B to the side AC using a compass.

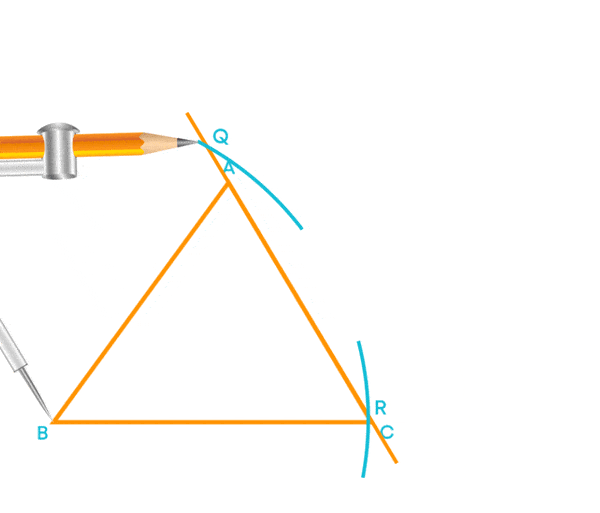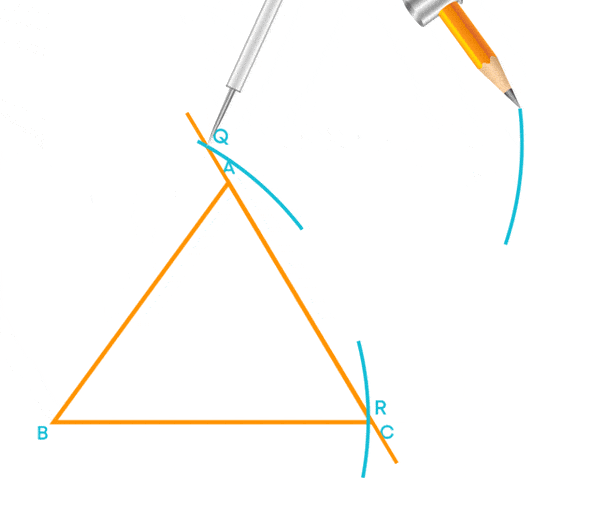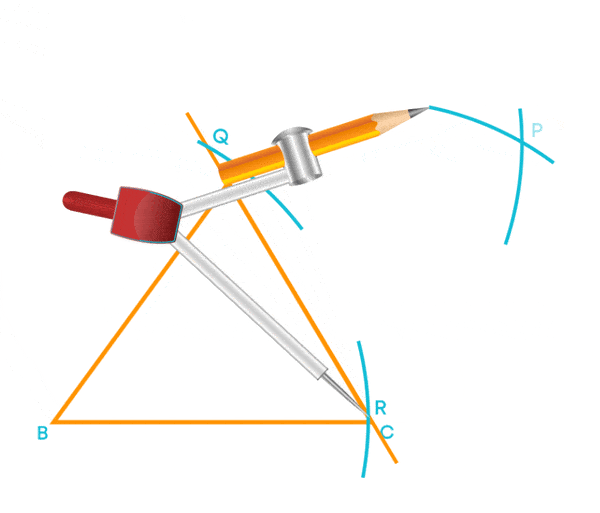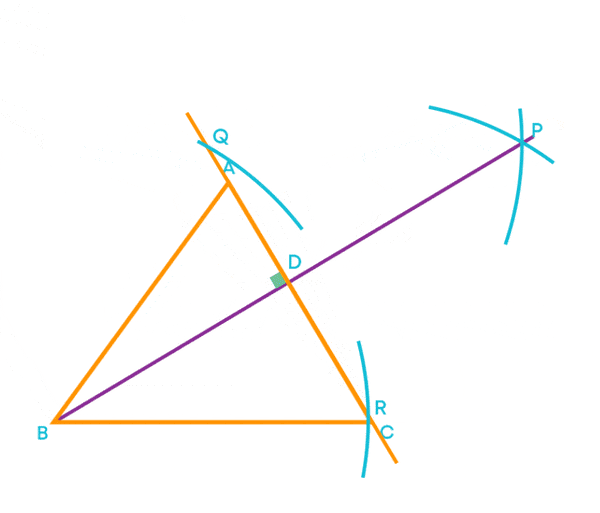
Now, the perpendicular line segment BD is the altitude of the triangle.
- Do the same procedure for the other two sides.

Here BD, CE, and AF are altitudes of the triangle ABC.
Exterior Angle of a Triangle and its Property
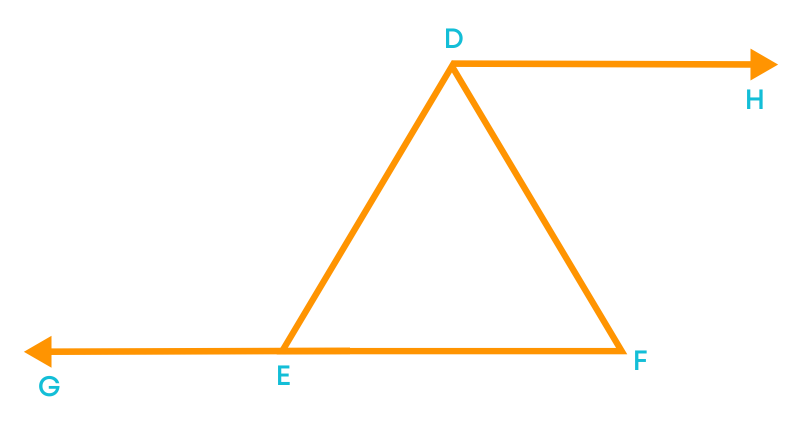
As we know, a triangle has three sides, three vertices and three angles. Now let us learn what an exterior angle of a triangle is. Consider the triangle ABC.
Now, extend the side BC of the ∆ABC.

By extending the side BC, we can see that angle ACD is formed. Does ∠ACD lie on the exterior of triangle ABC? Yes, we can see that ∠ACD lies on the exterior of triangle ABC. We call this angle as an exterior angle of ∆ABC.
An exterior angle of a triangle is an angle formed by one side of the triangle and the extension of an adjacent side of the triangle.
Let us learn how many exterior angles a triangle has. Consider the triangle PQR.
Now, extend all the three sides PQ, QR, and PR.
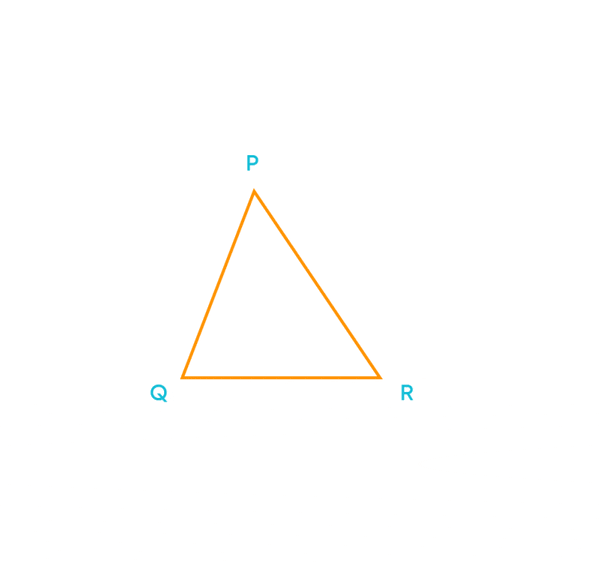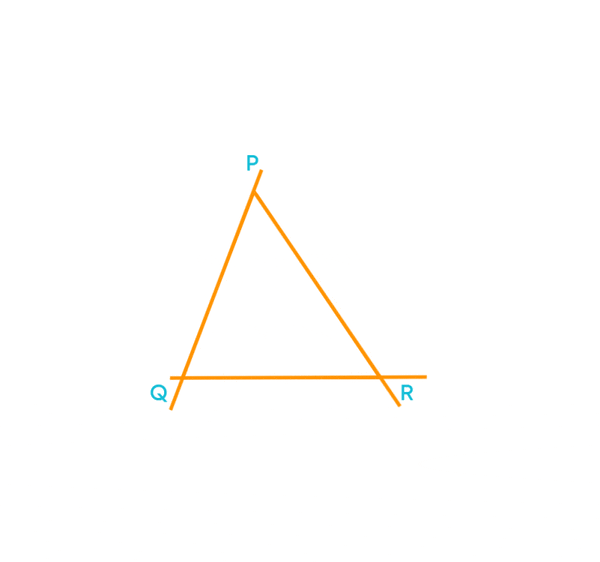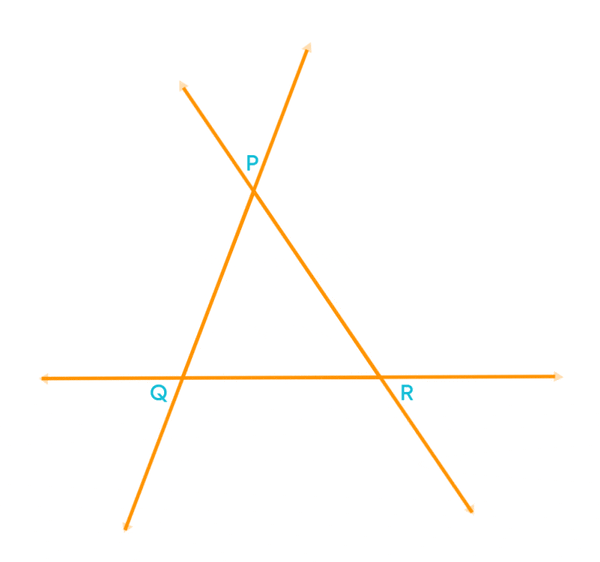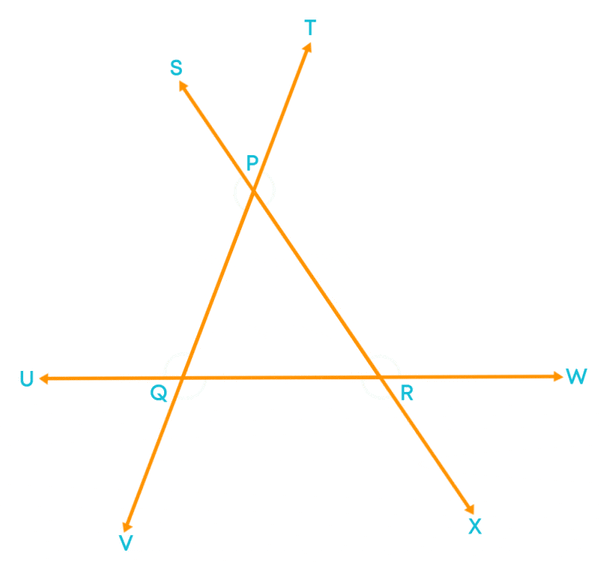
Now, we can see all the exterior angles of ∆PQR.
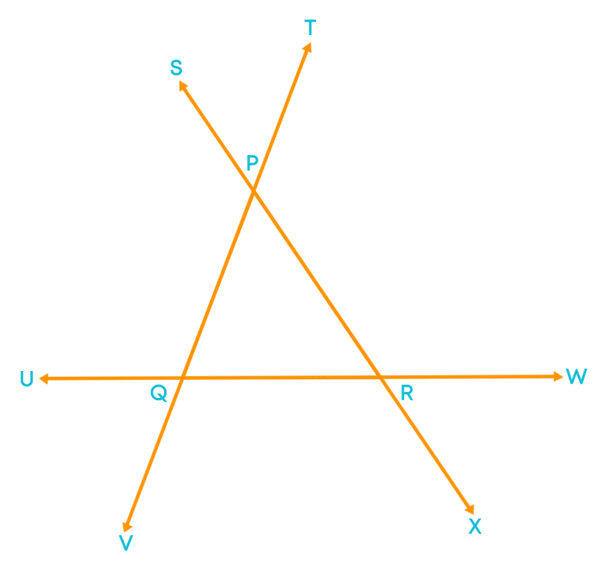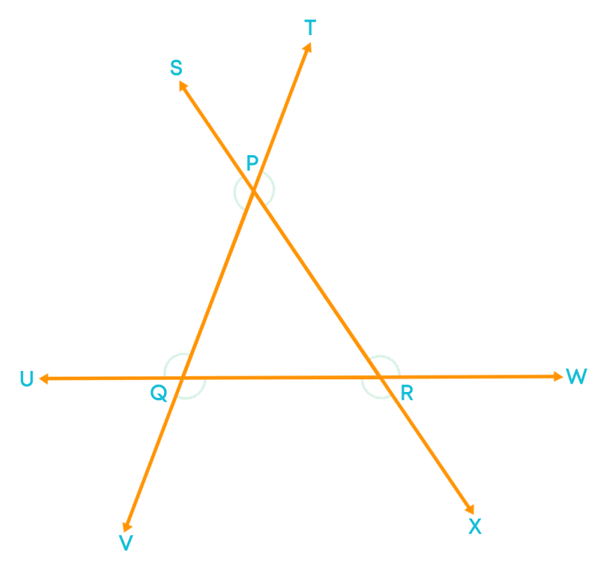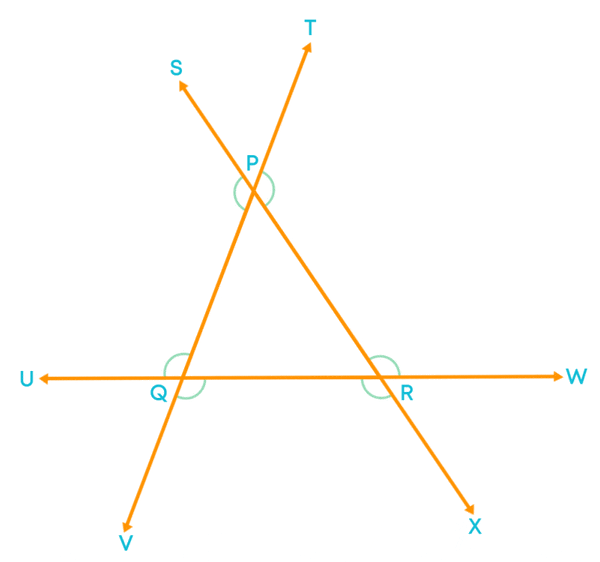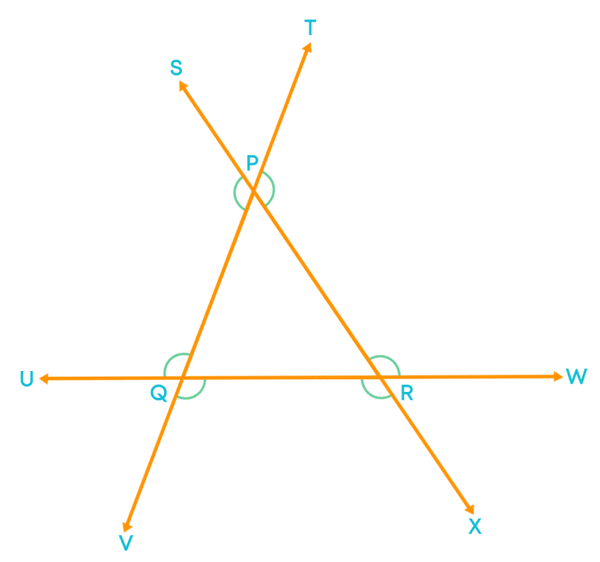
You know what exterior angle of a triangle is and how to identify them. Also, the angle which is adjacent to the exterior angle is known as the interior adjacent angle. For example,

You know what exterior angle of a triangle is and how to identify them. Also, the angle which is adjacent to the exterior angle is known as the interior adjacent angle. For example,
Here we call ∠DEF as an interior adjacent angle. Let us understand what an interior opposite angle in a triangle is. Consider ∆PQR with ∠PRS as an exterior angle.
Here ∠PRQ is the interior adjacent angle for the exterior ∠PRS.
The remaining two angles inside the triangle namely ∠PQR and ∠QPR are known as interior opposite angles.
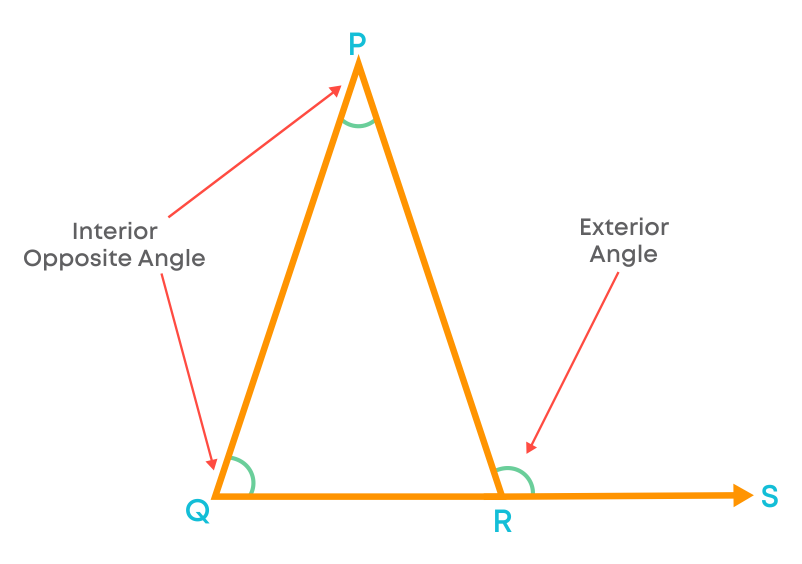
Interior opposite angles of an exterior angle of a triangle are the angles other than the interior angle which is adjacent to the exterior angle.
Exterior angle and the interior adjacent angle of a triangle form a linear pair.
An exterior angle of a triangle is equal to the sum of its interior opposite angles. Consider the ∆ABC with ∠ACD as the exterior angle. Through the vertex C, draw a line segment CE parallel to the line segment AB.
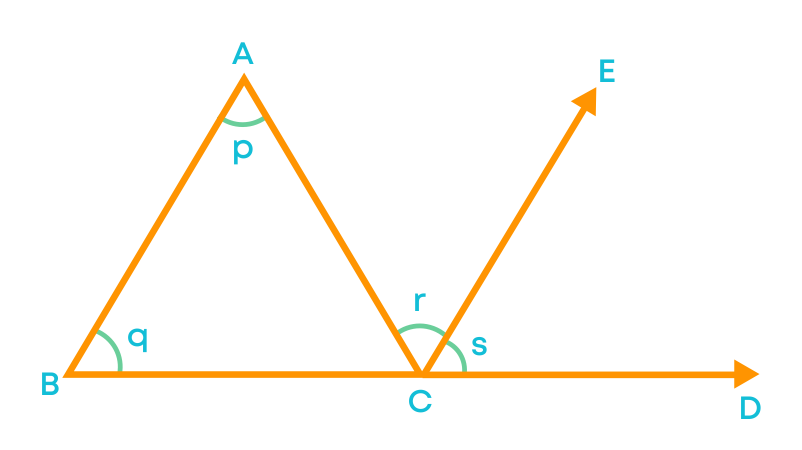
In the given figure, AB ‖ CE and AC is a transversal. Here ∠p and ∠r are alternate angles, so they are equal. So, ∠p = ∠r …………(i)
AB ‖ CE and BD is a transversal. Here ∠q and ∠s are corresponding angles, so they are equal. So, ∠q = ∠s ……….(ii)
On adding (i) and (ii) we get:
∠p + ∠q = ∠r + ∠s………..…(iii)
From the figure, we have ∠ACD = ∠r + ∠s………….(iv)
From the equation (iii) and (iv), we get:
∠ACD = ∠p + ∠q
Hence, we can conclude that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
Now, let us learn how to find the unknown angles using exterior angle property. Consider the question:
Find the value of the unknown exterior angle ‘x’ in the given figure.
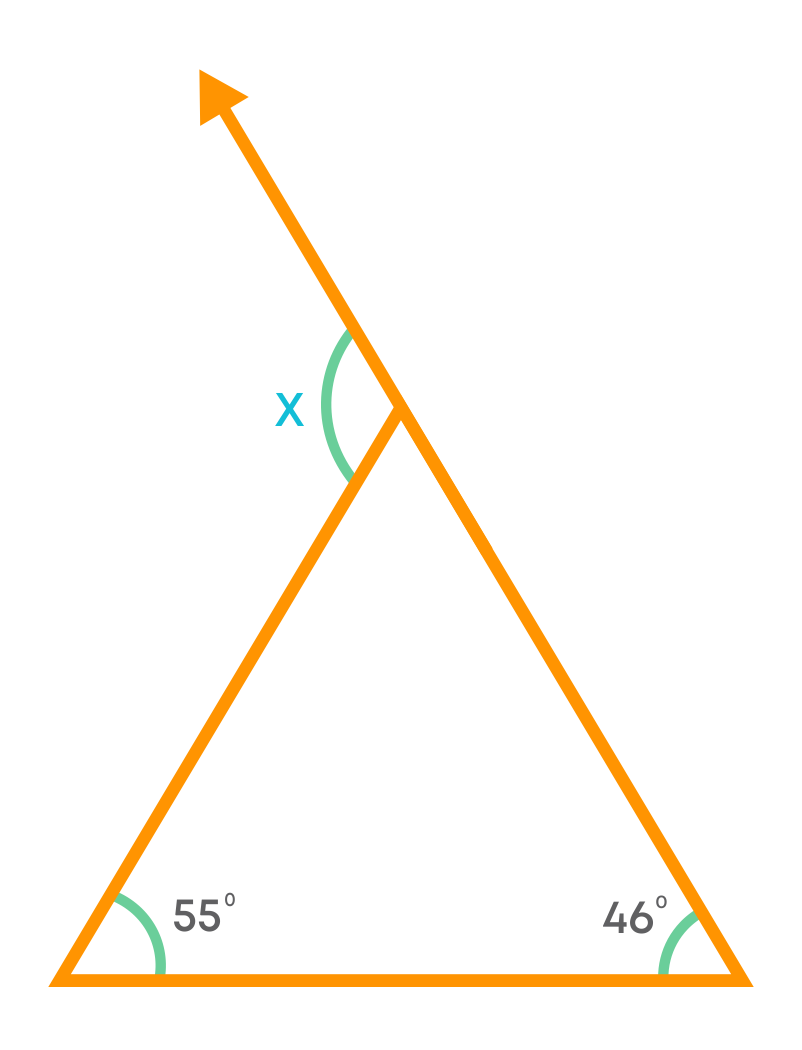
We can see that the values of the two interior opposite angles of ‘x’ are given in the figure above. Since an exterior angle is the sum of its interior opposite angles,
x = 55°+ 46° = 101°
Hence, the value of the exterior angle is 101°.
To find the measure of an exterior angle when the measures of the interior opposite angles are given, add the interior opposite angles.
Angle Sum Property of a Triangle
The sum of the measures of the three angles of a triangle is 180⁰.
Consider the triangle ABC.

The angles on a straight line add up to 180 degrees.
Sum of the angles in a triangle = 180⁰
Now, let us justify the angle sum property of a triangle. Let us prove this using the exterior angle property of a triangle. Consider the triangle PQR and extend the side QR.
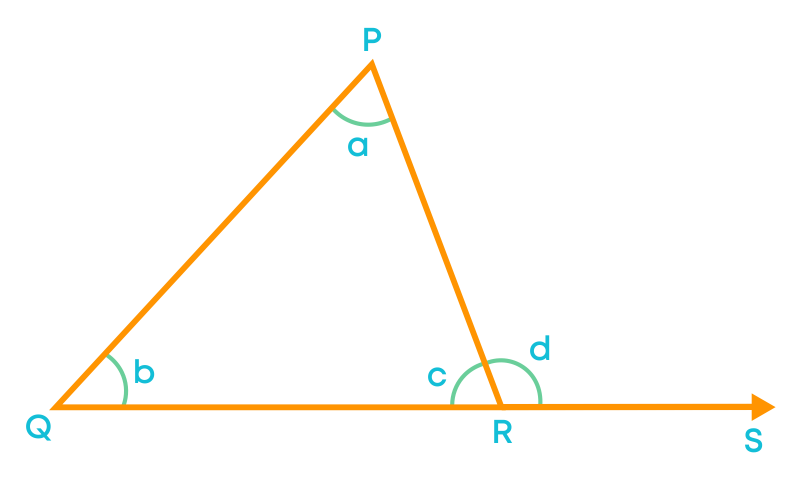
Here, ∠a, ∠b, and ∠c are the angles in ∆PQR and ∠d is an exterior angle.
Using the exterior angle property,
∠a + ∠b = ∠d
Now, on adding ∠c on both sides, we get:
∠a + ∠b + ∠c = ∠d + ∠c
∠d and ∠c form a linear pair, so
∠d + ∠c = 180⁰
Hence, ∠a + ∠b + ∠c = 180⁰
So, the total measure of the three angles of a triangle is 180⁰.
Now, let us apply this property to solve some problems. Consider the following question:
Is it possible to have a triangle with all the three angles greater than 60⁰?
Let us take the three angles, 65⁰, 62⁰, and 71⁰.
We know that the sum of the three angles of a triangle should be180⁰. But 65⁰ + 62⁰ + 71⁰ = 198⁰.
Here we can see that the sum of these three angles is greater than 180⁰. So, it is not possible to have a triangle with all the three angles greater than 60⁰.
Consider the question:
Find the value of the unknown angle ‘t’ in the given figure.
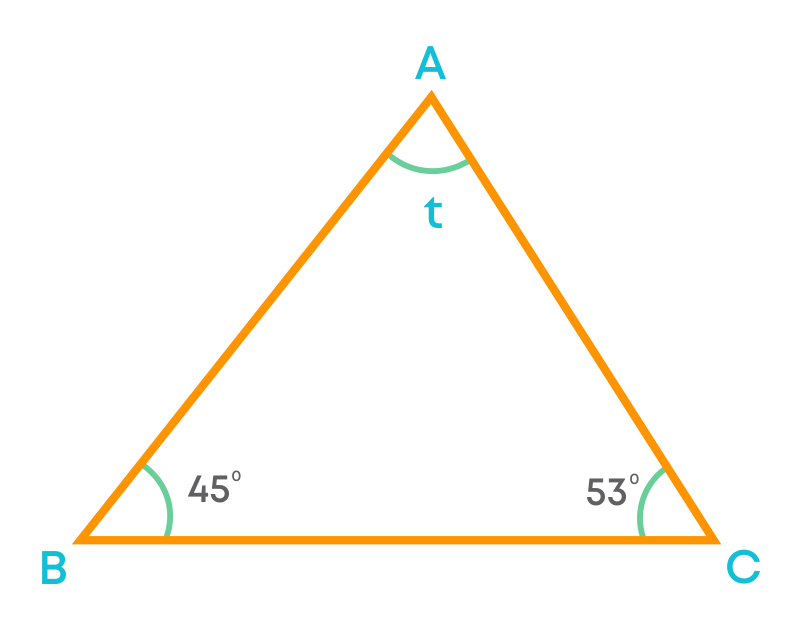
The sum of the measures of three angles is 180⁰. From the figure,
45 + 53 + t = 180
98 + t = 180
So, t = 180 – 98 = 82⁰

Two Special Triangles – Equilateral and Isosceles
Consider the triangle ABC.
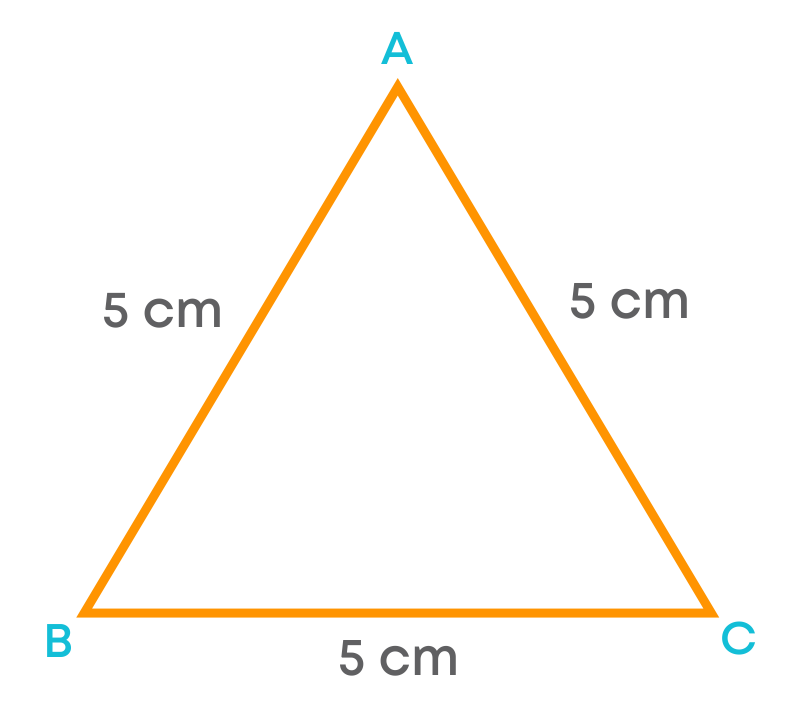
We can see that the length of side AB = side BC = side AC. So, the triangle ABC is called an equilateral triangle.
A triangle in which all the three sides are of equal length is called an equilateral triangle.
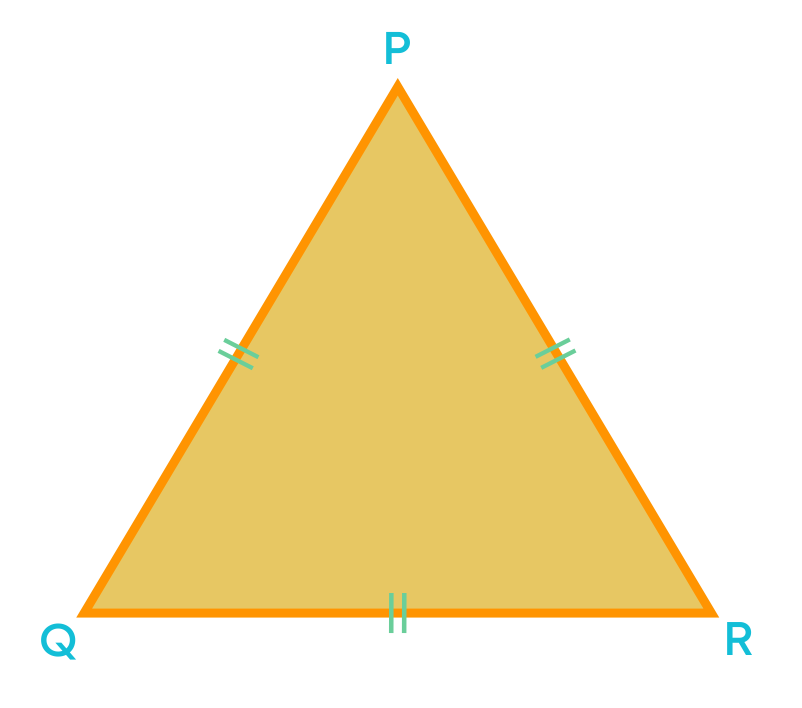
Here, ∆PQR is an equilateral triangle.
Consider the equilateral triangle KLM,

We have, Length KL = length LM = length KM. When the three sides of a triangle have equal lengths, then the three angles will also be of equal measure.
∠K = ∠L = ∠M
The sum of the measures of the angles of a triangle is 180⁰ (angle sum property).
Since the angles are equal, the measure of each angle will be 180 ÷ 3 = 60⁰.
Therefore, ∠K = ∠L = ∠M = 60⁰
So, in an equilateral triangle,
- 1. All sides are equal.
- 2. All angles are equal and measure 60⁰ each.
Now, consider the triangle KLM.
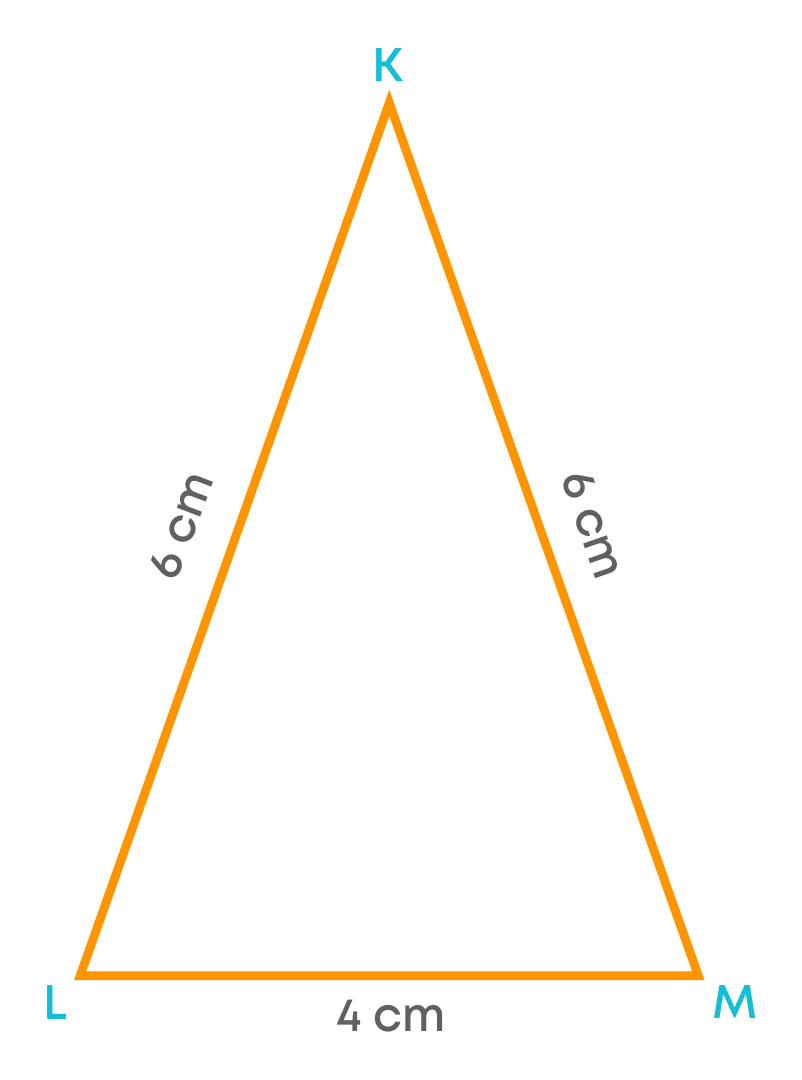
We can see that the length of side KL = side KM. As only the two sides are equal in length, the triangle is not an equilateral triangle. Do you know what a triangle having only two of its sides equal is called?
A triangle in which two sides are of equal length is called an isosceles triangle. For an isosceles triangle ABC, the length of side AB = side AC,
- AB and AC are of equal length
- BC is called the base.
- The angles which are opposite to the equal sides are known as base angles
Here ∠B and ∠C are called base angles:
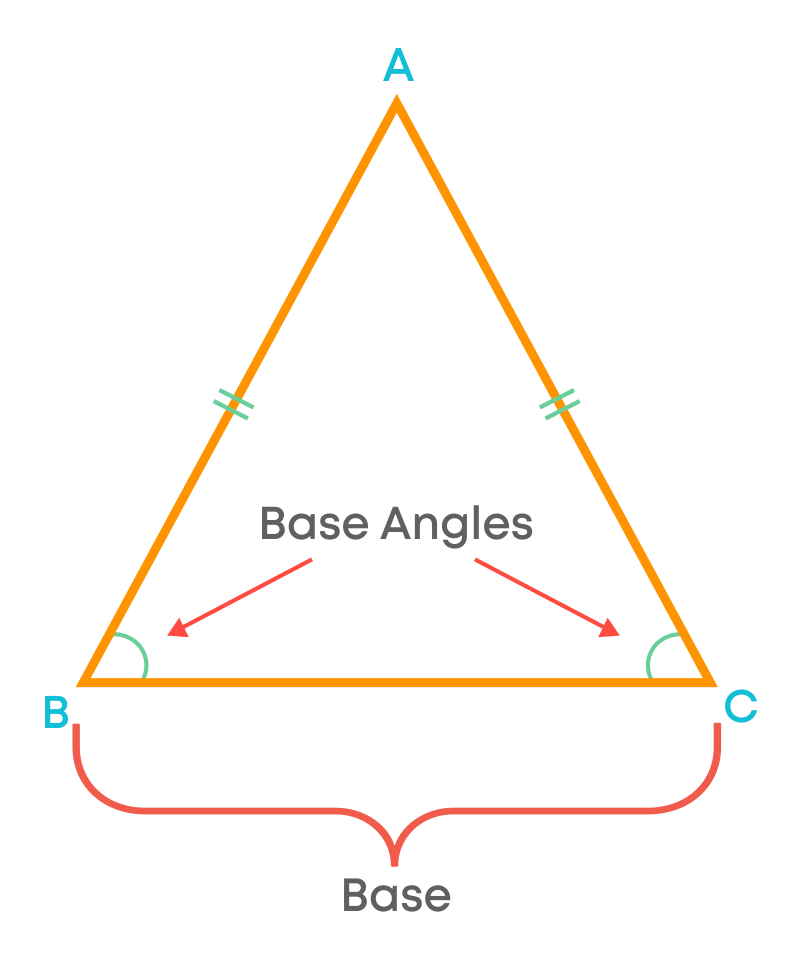
In an isosceles triangle:
- Two sides have the same length.
- Base angles opposite to the equal sides are equal.
Consider the following question:
In an isosceles triangle, if each of the base angles is 30⁰, then is the triangle is right-angled, obtuse – angled, or acute - angled?
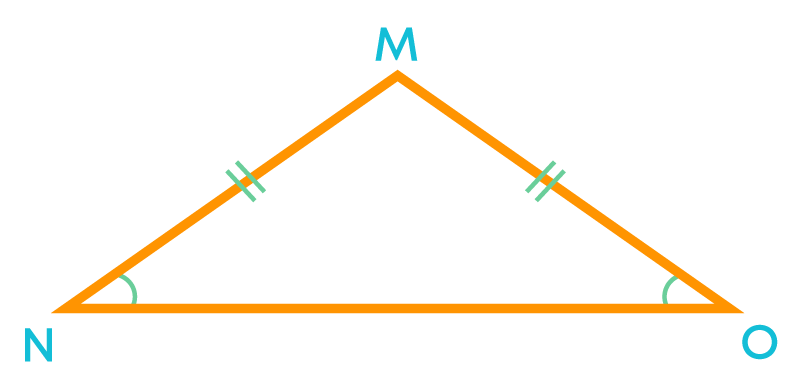
In the given figure, let side ON be the base of ∆MNO and ∠O = ∠N = 30⁰.
MN = MO
Now, ∠M + ∠N + ∠0 = 180⁰ (angle sum property)
∠M = 180 – 30 – 30 = 120⁰ (each base angle is 30⁰)
Thus, ΔMNO is an obtuse - angled triangle.
Sum of the Lengths of The Two Sides of a Triangle
The sum of the lengths of any two sides of a triangle will be greater than the third side.
Let us take a triangle with the sides
- AB = 6 cm
- BC = 4 cm
- AC = 7 cm
Here the sum of the lengths of the two sides of the triangle is greater than the third side, i.e.,
- 6 + 4 = 10 > 7
- 4 + 7 = 11 > 6
- 7 + 6 = 13 > 4

We can see the triangle formed with the given measurements. Now, let us take a triangle with the sides 6 cm, 4 cm, and 11 cm. Here, 6 + 4 = 10 < 11, i.e., the sum of the lengths of the two sides of a triangle is less than the third side.
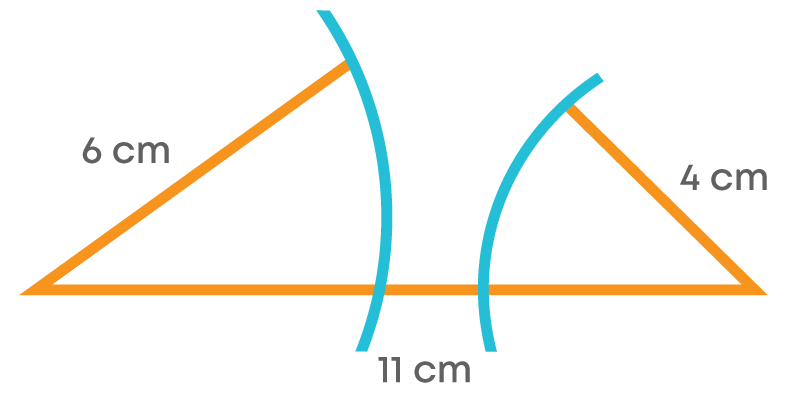
Here, we cannot form the triangle with the given measurements.
The difference of the lengths of any two sides of a triangle will be less than the third side.
Let us take a triangle with the sides 6 cm, 4 cm, and 7 cm. Here the difference of the lengths of the two sides of a triangle is less than the third side,
i.e., 6 - 4 = 2 < 7
7 – 4 = 3 < 6
7 - 6 = 1 < 4
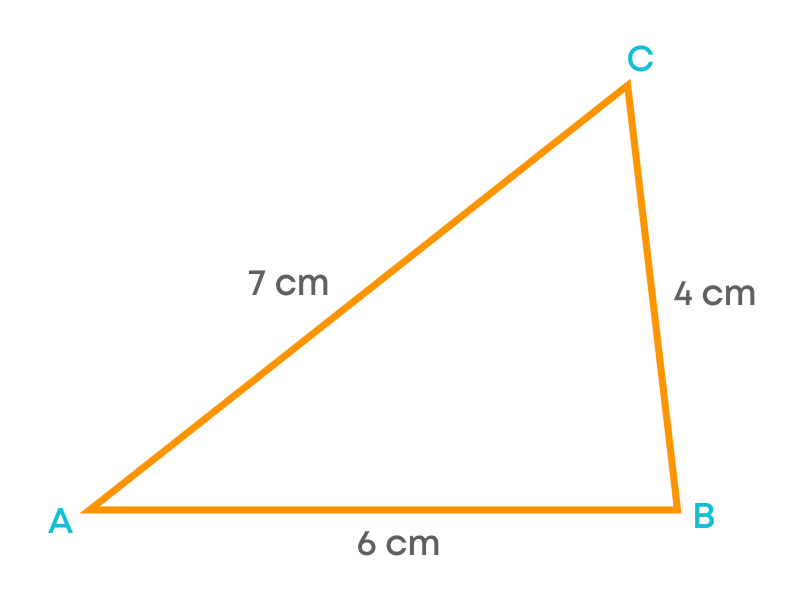
Here, we can see that the triangle can be formed. Now, let us take a triangle with the sides 6 cm, 4 cm, and 11 cm. Here,
11 – 6 = 5 > 4
i.e., the difference of the lengths of two sides of a triangle is greater than the third side.
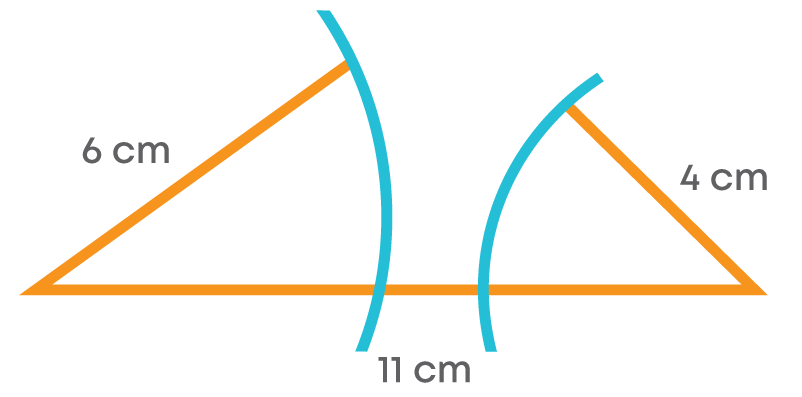
Here, we cannot form the triangle.
Consider the question:
The sides of a triangle have lengths (cm) 13, 8.5 and ‘b’, where ‘b’ is a whole number. Find the minimum value that ‘b’ can take?
- As we know, the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
So, 13 + 8.5 > b
i.e., 21.5 > b
- Also, the difference of any two sides of a triangle is less than the length of the third side.
So, 13 – 8.5 < b
- i.e., 4.5 < b
So, the value of ‘b’ should be greater than 4.5 and less than 21.5.
Since ‘b’ is a whole number, the nearest whole number which is greater than 4.5 is 5. So, the minimum value that ‘b’ can take is 5.
Right-Angled Triangles and the Pythagoras Property
Consider the right-angled triangle ABC.
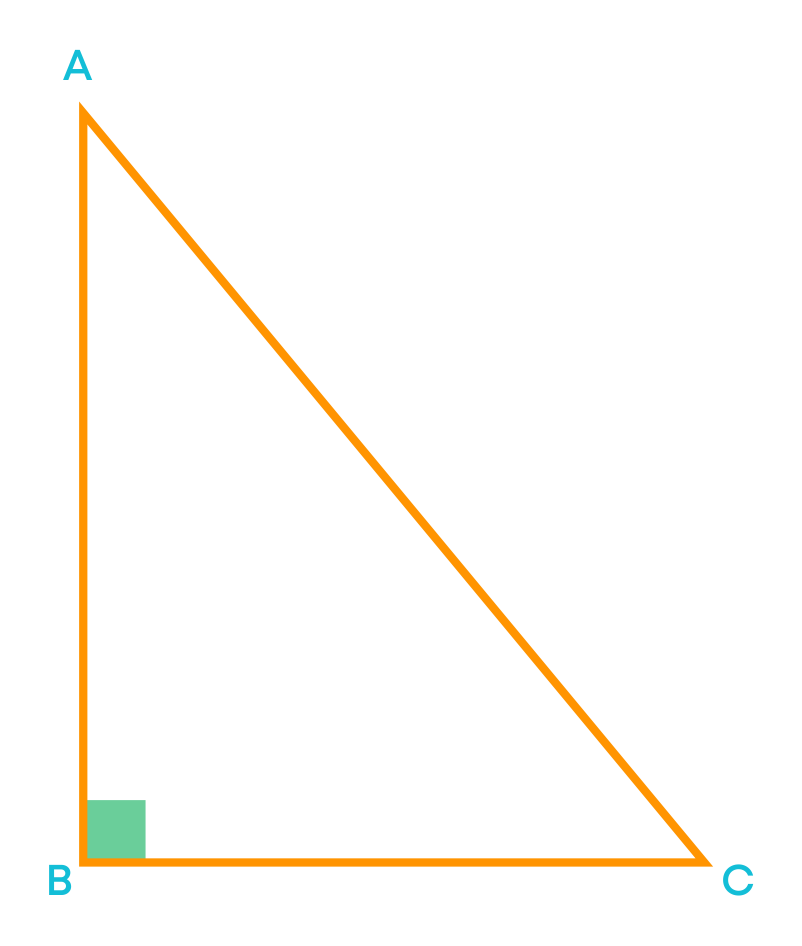
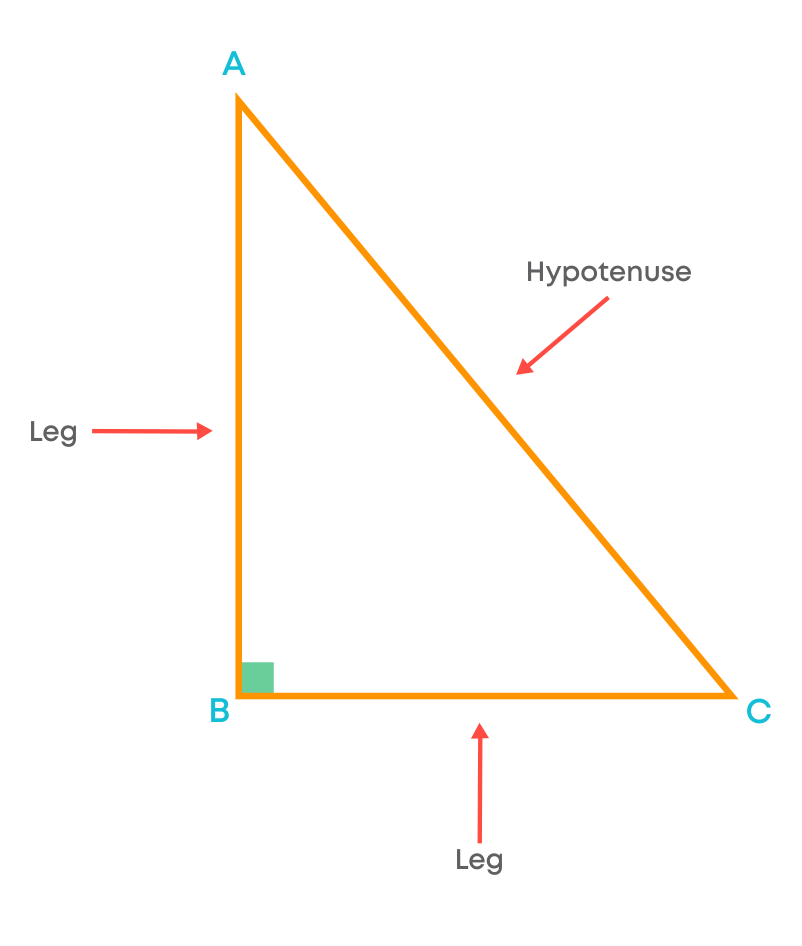
The sides of a right-angled triangle have special names:
- The side opposite to the right angle is called the hypotenuse.
Here, AC is the hypotenuse of the right-angled triangle.
- The other two sides are known as the legs of the right-angled triangle.
Here, AB and BC are called the legs of the right-angled triangle.
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of its legs. For example, consider the right-angled ∆XYZ.
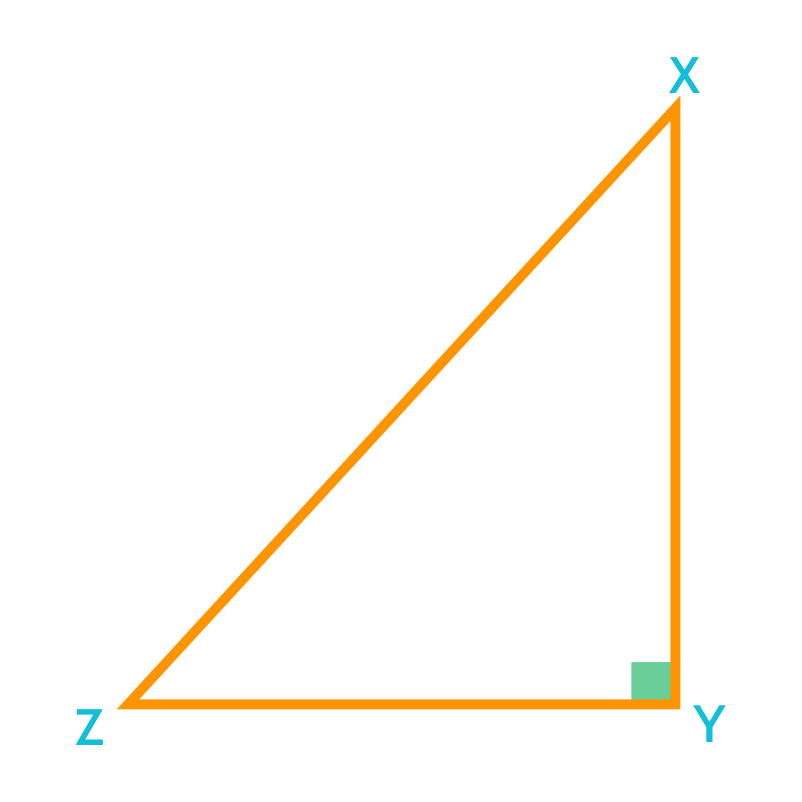
Here, XZ2 = XY2 + ZY2
This is the Pythagoras theorem or property which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of its legs.
Now, let us define the converse of Pythagoras property. The converse of the Pythagoras property states that if the Pythagoras property holds, then the triangle must be right-angled.
Let us check if the Pythagoras property holds good for the other type of triangles as well.
Let us take an acute-angled triangle with sides 6 cm, 4 cm, and 5 cm.
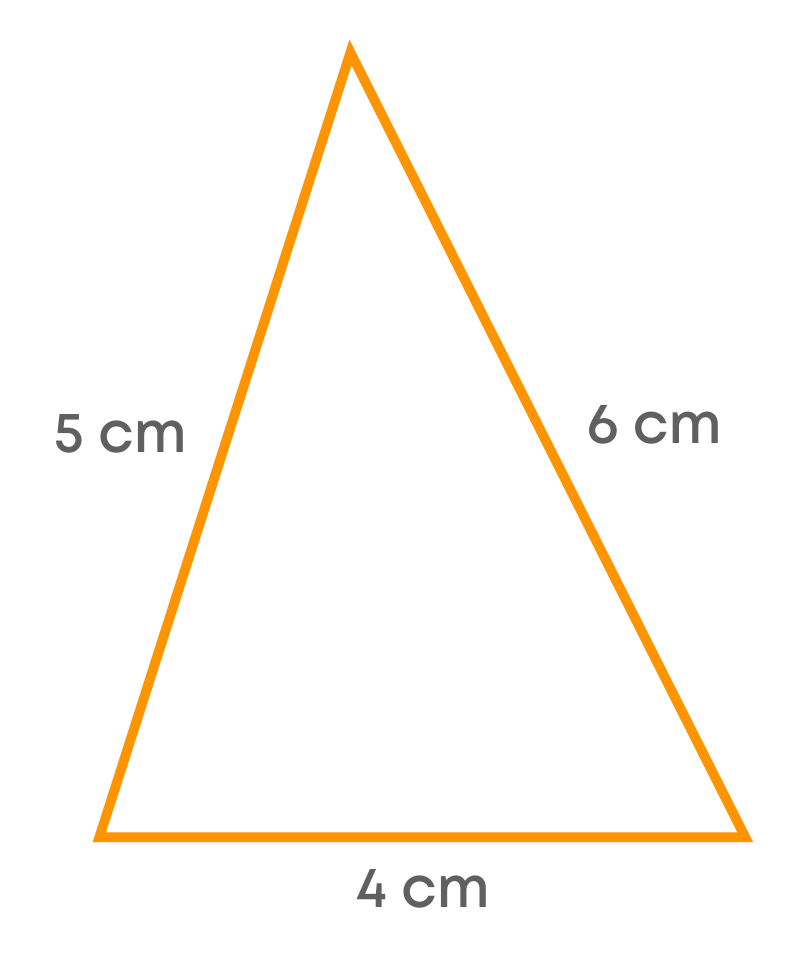
Here 62 ≠ 52 + 42
From this, we can see that if Pythagoras property holds then the triangle must be a right-angled triangle. So, we can apply the Pythagoras property to check whether the triangle is right-angled or not. What do we infer from this?
If the square of the longest side is equal to the sum of the squares of the other two sides, then the triangle is a right-angled triangle.
Remember, in any right-angled triangle, the hypotenuse is the longest side.
Let us now learn how to find the unknown side using the Pythagoras property. Consider the question:
Find the unknown length ‘a’ in the given figure:
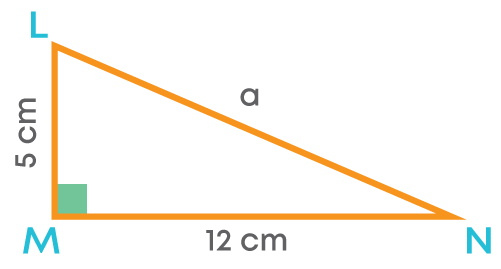
Given a right-angled triangle with sides LM = 5 cm and MN = 12 cm.
We must find the unknown length ‘a,’ i.e., the length of the hypotenuse LN.
We can apply Pythagoras property to solve this question. Since the square of the hypotenuse is equal to the sum of the squares on its legs, LM2 + MN2 = LN2
i.e., 52 + 122 = a2
25 + 144 = a2
169 = a2
Therefore, a = 13 cm.
Consider the question given below.
The foot of a ladder is 9 m away from its wall and its top reaches a window 12 m above the ground. Find the length of the ladder.
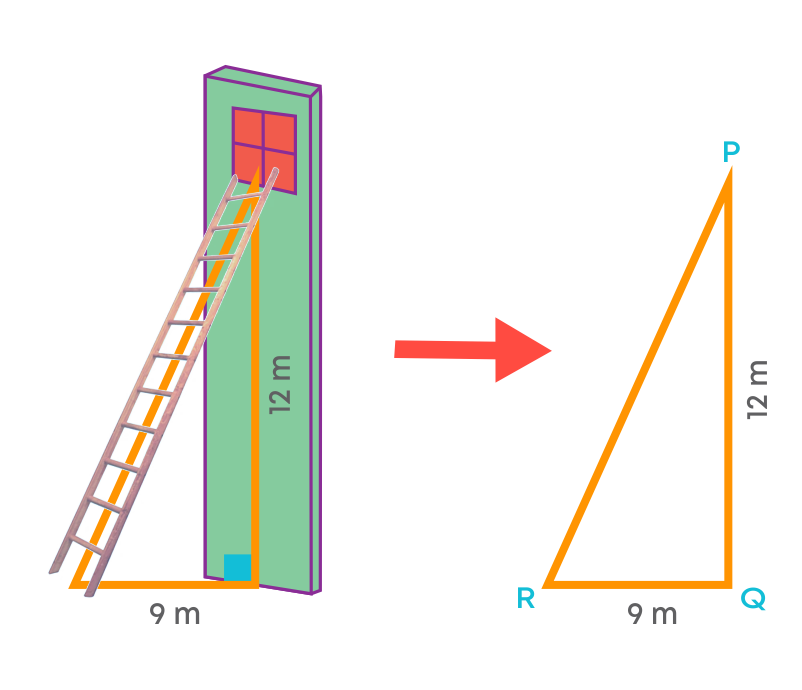
(i) Let PQ be the distance between the ground and the window on the wall, and RQ be the distance of the foot of the ladder from the wall. Let PR be the length of the ladder. By applying the Pythagoras property,
PQ2 + RQ2 = PR2
122 + 92 = PR2
PR2 = 144 + 81 = 225
So, PR = 15 m, i.e., the length of the ladder is 15 m.
Common Errors
The following are topics in which students make common mistakes when dealing with triangles and their properties:
- 1. Identify medians
- 2. Identify altitudes
- 3. Identify the exterior angle of the triangle
Identify Medians
Median is the line segment joining the vertex of a triangle and the midpoint of its opposite side. So, to identify the medians we should check if the line segment bisects the opposite side or not. For example, in the below triangle the line segment XW bisects the side YZ, so XW is the median.
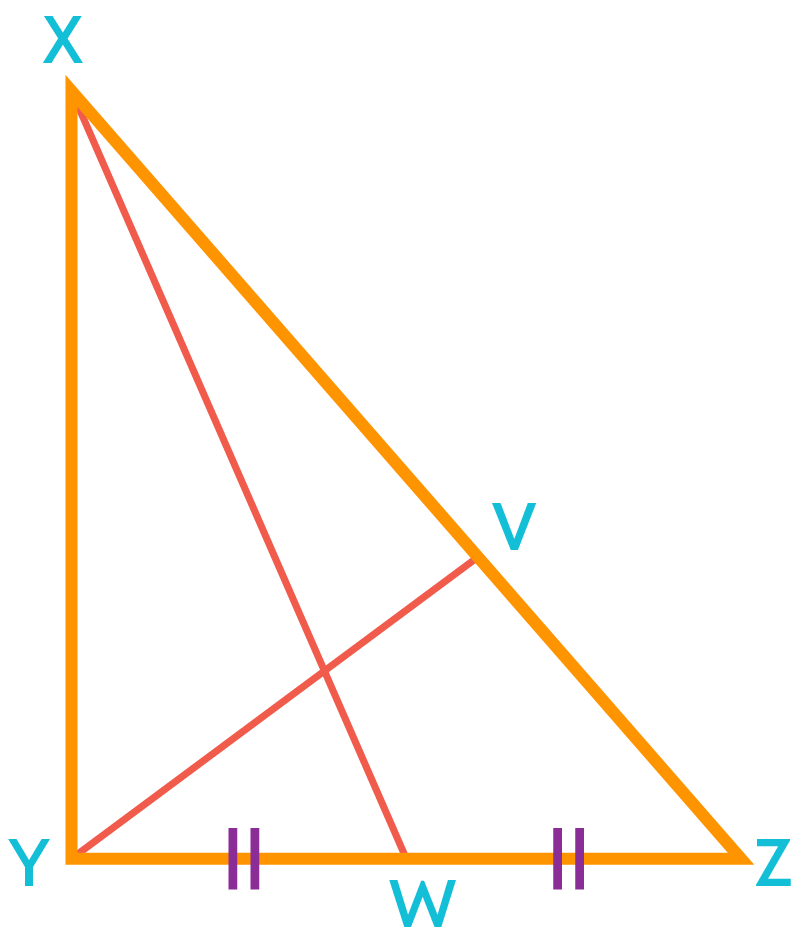
But the line segment YV does not bisect the side XZ, so it is not a median.

Identify Altitudes
Altitude is the perpendicular line segment from a vertex of a triangle to its opposite side. So, to identify the altitude we should check whether the line segment is perpendicular to its opposite side or not. For example, in the given triangle ABC, the line segment AD is perpendicular to the side BC, so it is an altitude.
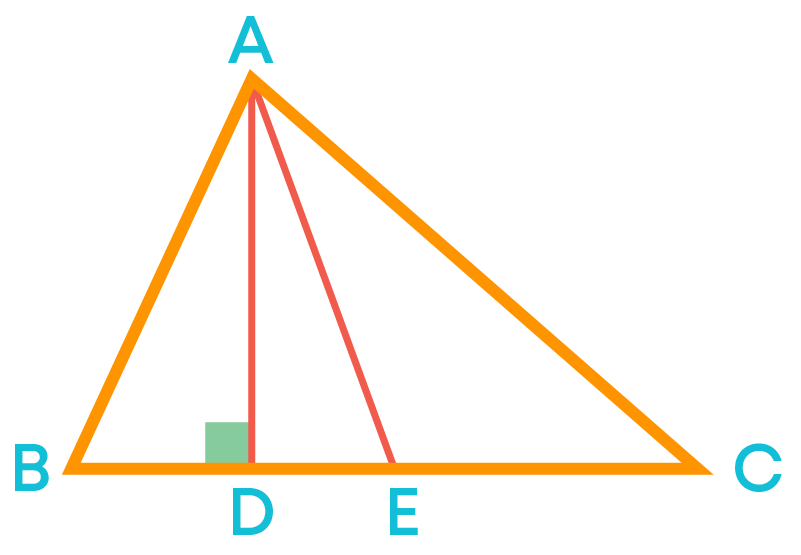
But the line segment AE is not perpendicular to the side BC, so it is not an altitude.

Identify The Exterior Angle Of The Triangle
The exterior angle of a triangle is an angle formed by one side of the triangle and the extension of an adjacent side of the triangle. To identify the exterior angle of a triangle check whether the angle is formed by the one side of a triangle and the extended adjacent side. For example, look at the figure given below.
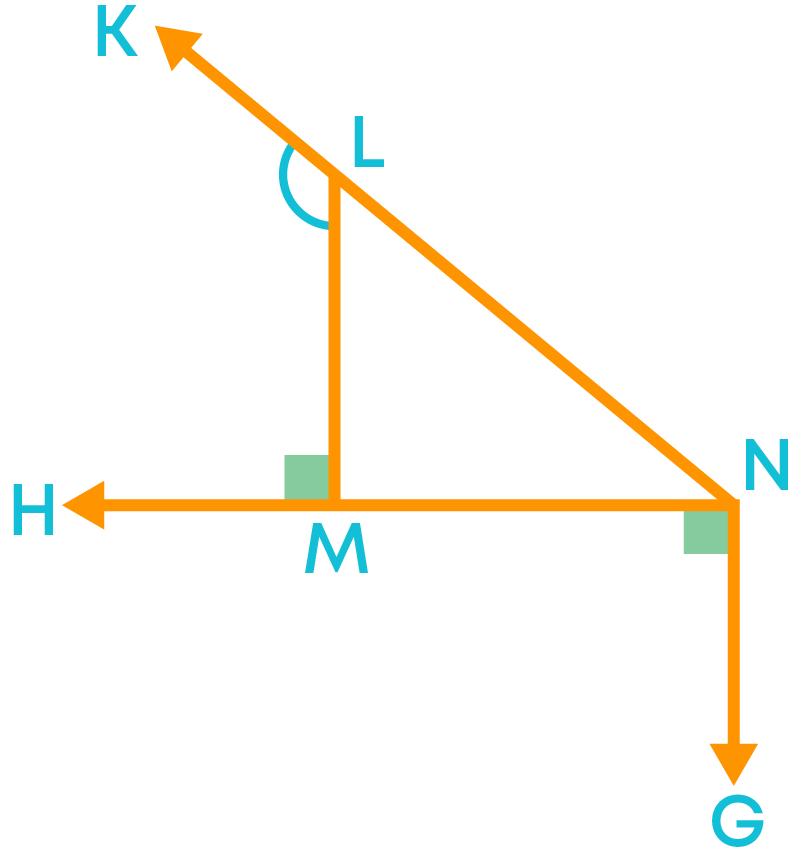
Here, ∠KLM and ∠LMH are exterior angles.
- ∠KLM is an exterior angle since it is the angle between the side LM and the extended side NL.
- ∠LMH is an exterior angle since it is the angle between the side LM and the extended side MN.
But ∠MNG lies on the exterior in ∆LMN, but it is not an exterior angle since it is not the angle between the extended sides MN or LN.

Conclusion
A lot of objects in our day-to-day lives resemble triangles. From your pizza slices, sandwiches, traffic signs, clothes hangers, and Toblerone chocolate, to the Egyptian Pyramids and other such structures – triangles are all around us. Hence, it is important to learn about their properties.
Can you solve this riddle based on triangle and its properties?
How many right-angle triangles can you find in the image?