Introduction
Decimal numbers are decimal fractions whose denominators are 10, 100, 1000, etc.
Let us take one square and divide this square into ten equal parts.

This coloured part represents 1/10. We can writer 1/10 as 0.1. Here 0.1 is a decimal.
Let us understand the relationship between decimal and fractions.
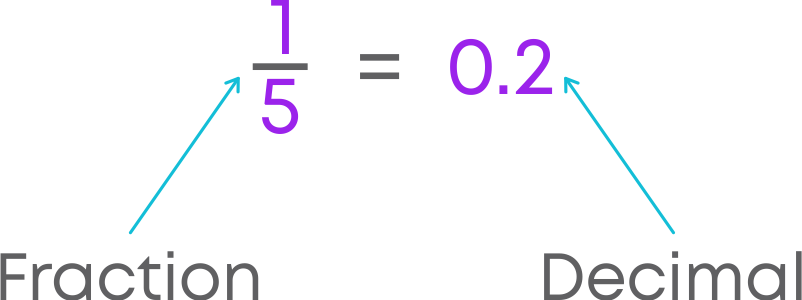
Let us look around and understand where we use decimals in our daily life. Watch the video below.
Concepts
The chapter ‘Decimals’ covers the following concepts:
Understanding Decimal Numbers
As you know, whole numbers have hundreds, tens, and ones. Can you tell which number is represented in the figure below?
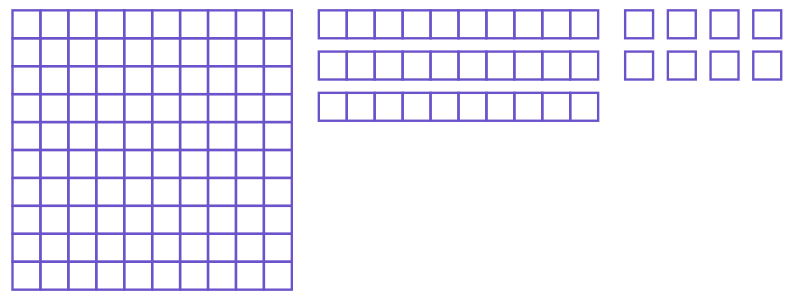
In this figure, there are 8 ones, 3 tens, and 1 hundreds. So, the number = 100 + 30 + 8 = 138.
Let us learn how to write and understand decimal places – Tenth, Hundredth and Thousandth.
Let us take the number 238. As you know, in 238, there are 8 ones since 8 is in the ones place, 3 tens since 3 is in the tens place, and 2 hundreds since 2 is in the hundreds place.
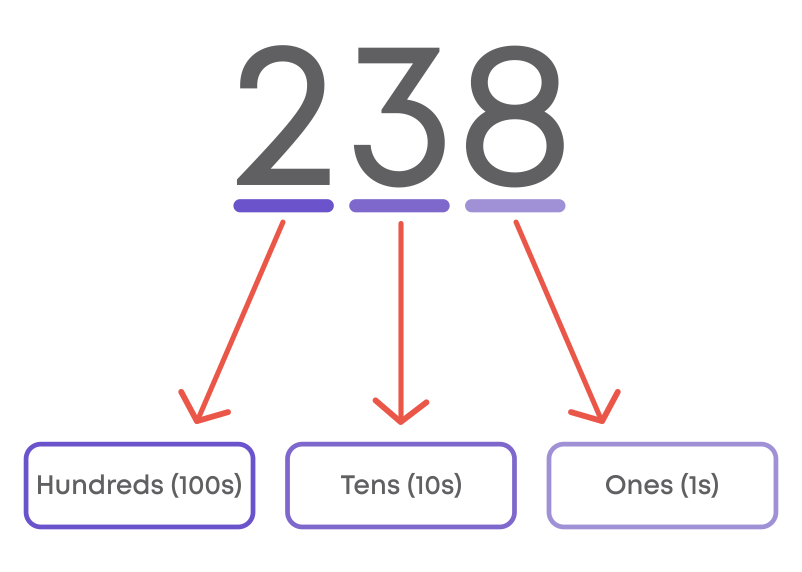
i.e., 200 + 30 + 8 = 238

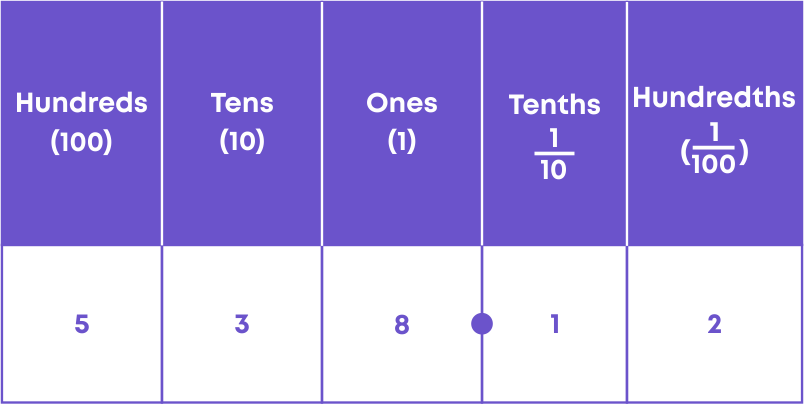
Now, let us learn about decimal place values in decimal numbers. Take the decimal number 238.56
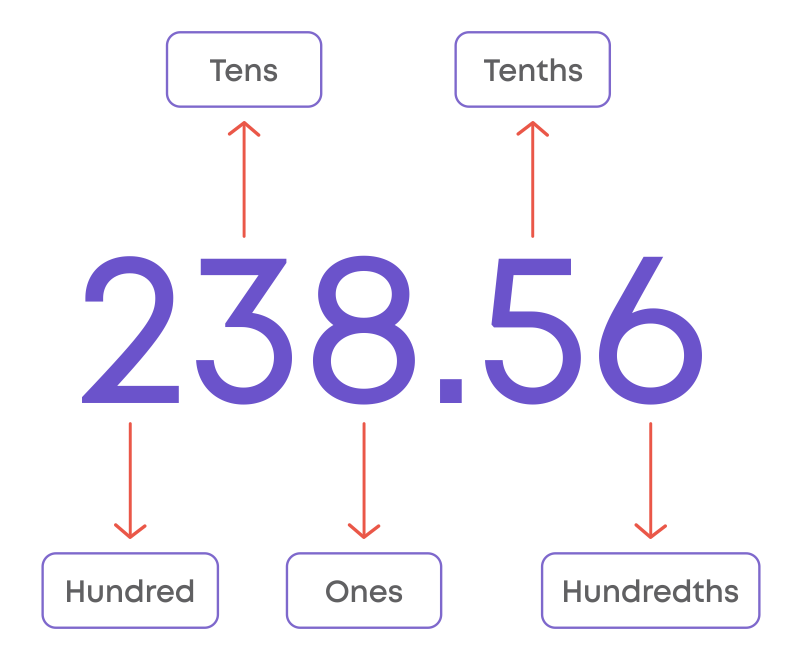
We can also represent this numbers in the figure as below.

On the left of the decimal point is a whole number.
i.e., In 238.56, 238 is a whole number.
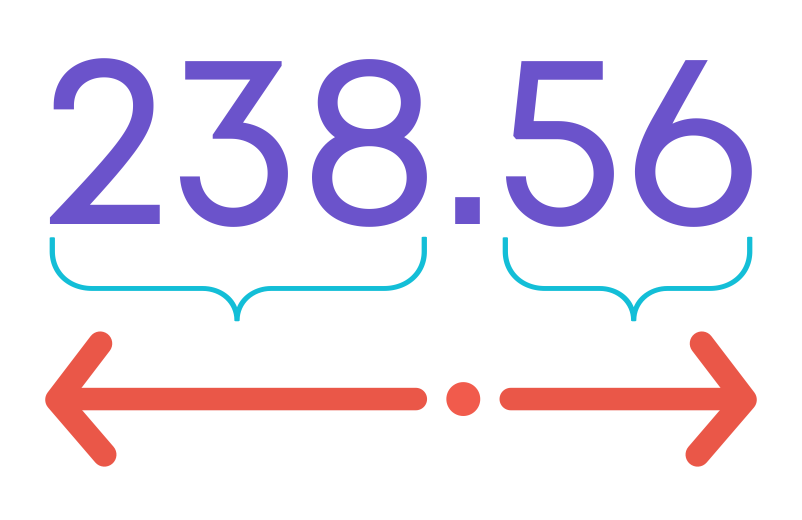
As we move further to the left of the decimal point, every place gets 10 times bigger.
i.e., 8 is at ones(1) place, 3 is at tens(10) place and 2 is at hundreds(100) place.
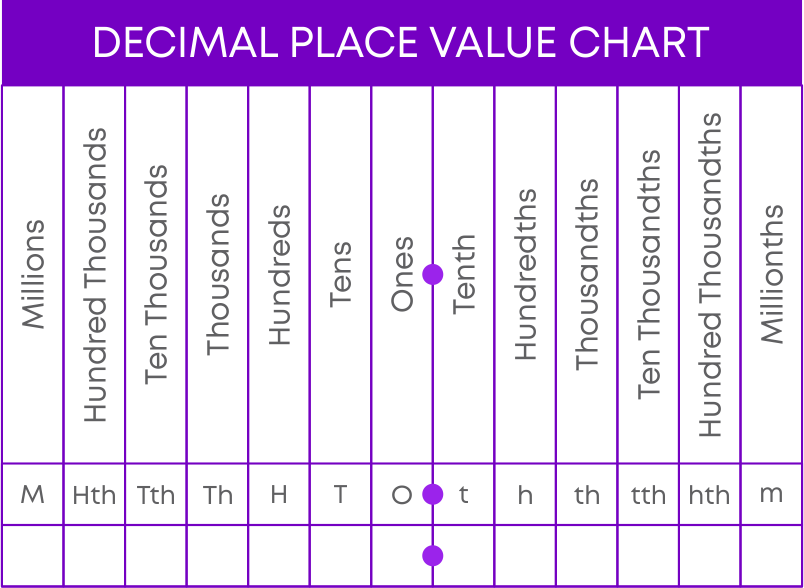
The first digit after the decimal point is tenths, i.e., 1/10. After tenths place, there is hundredths place, i.e., 1/100.
As we move to the right of the decimal point, every place gets 10 times smaller. A decimal place value chart looks like this.
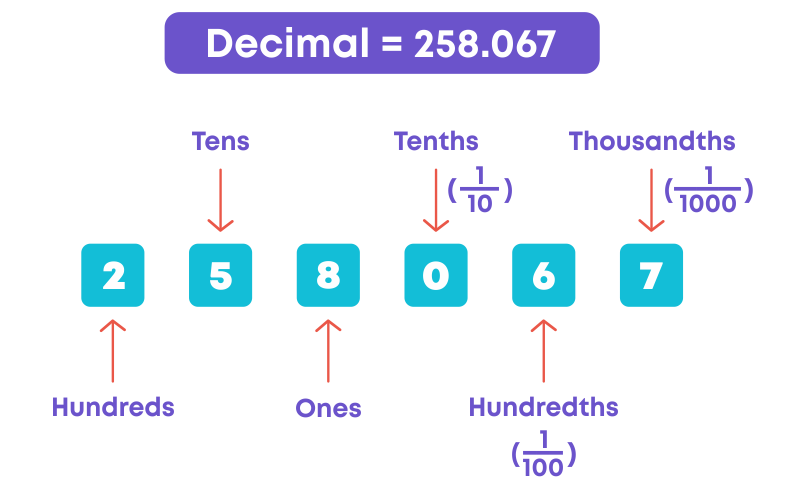
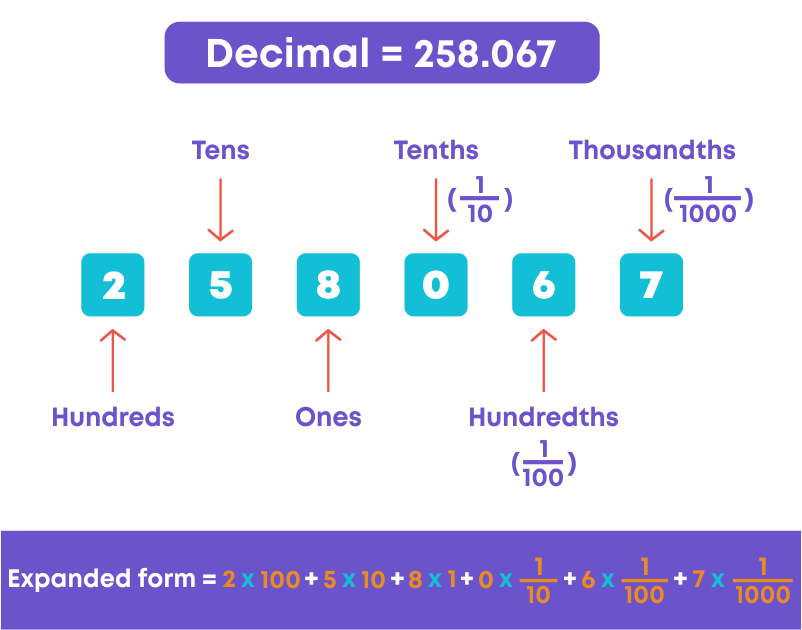
We already know how to expand whole numbers as the sum of thousands, hundreds, tens, and ones. Now, let us learn how to write the expanded form of decimal numbers. Consider the decimal number 258.067. This decimal has 2 hundreds, 5 tens, 8 ones, no tenths, 6 hundredths and 7 thousandths.
- Writing decimals in expanded form means writing each number according to its place value.
- This is done by multiplying each digit by its place value and adding them together.
i.e.,
As we know, decimal numbers have decimal places tenths, hundredths, thousandths etc. Consider the decimals 2.65, 8.06 and 4.89. What do you notice? Here 2.65, 8.06 and 4.89 has 2 decimal places.
i.e., They have the same number of decimal places. Such decimals are called like decimals.

In other words, 2.65, 8.06 and 4.89 have the same number of digits to the right of the decimal point.
Now, consider the decimals 0.8, 6.35, 1.208. What do you notice? Here 0.8, 6.35 and 1.208 have different number of decimal places. Such decimals are called unlike decimals.

In other words, 0.8, 6.35 and 1.208 do not have the same number of digits to the right of the decimal point.
Let us learn how to place decimals in the place value table. As we know,
- The first digit after the decimal represents the tenths place.
- The next digit after the tenths place represents the hundredths place.
- The next digit after the hundredths place represents the thousandths place.
Let us consider the decimal number 538.12. In this number 5 is at the hundreds place, 3 is at the tens place, 8 is at the ones place, 1 is at the tenths place and 2 is at the hundredths place.
i.e.,
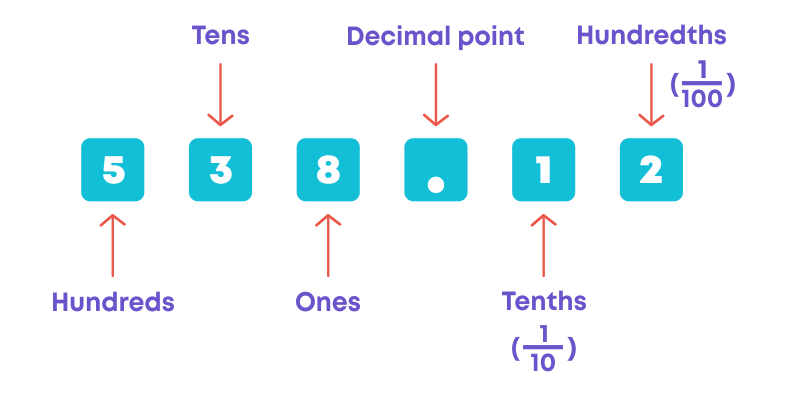
To place 538.12 in the place value table, we should place 5 at the hundreds place, 3 at the tens place, 8 at the ones place, 1 at the tenths place and 2 at the hundredths place. Representation of 538.12 in the place value table is as follows:
Let us know how to write the numbers given in the place value table in decimal form. Consider:
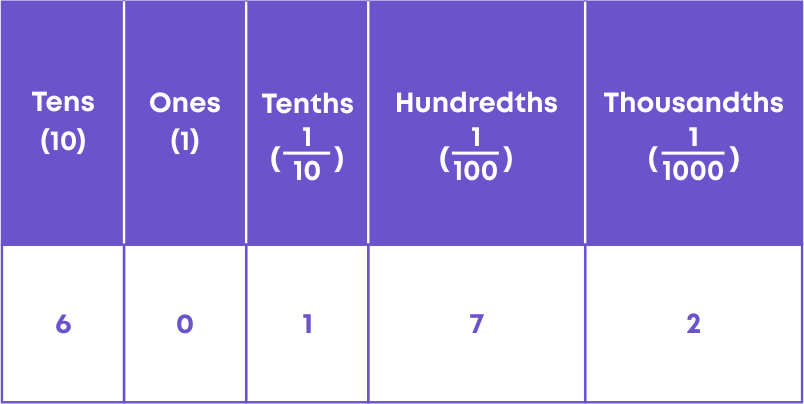
By observing this table, we can see that the decimal number will have 6 tens, no ones, 1 tenths, 7 hundredths and 2 thousandths. Hence, the decimal number
= 6 × 10 + 0 × 1 + 1 × 1/10 + 7 × 1/100 + 2 × 1/1000
= 60 + 1/10 + 7/100 + 2/1000
= 60.172
Let us learn, how to write numerical decimals in word form. Consider the decimal number 235.29. Let us place this number in the place value table.
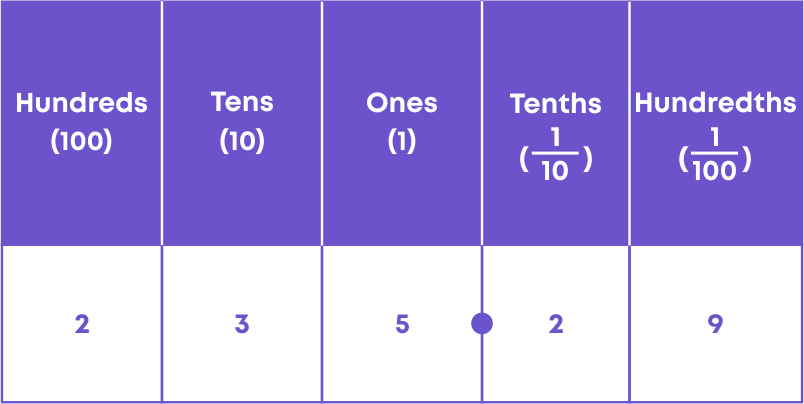
You can see that it has 2 hundreds, 3 tens, 5 ones, 2 tenths and 9 hundredths. We read the number as “Two hundred and thirty-five and twenty- nine hundredths”. Also, we can read that as “two thirty-five point two nine.”
Writing the word form of decimals in numerical form is the inverse process of writing numerical decimals in word form. Consider forty-six and two tenths.
Forty-six and two tenths can be written as 46 + 2 × 1/10 = 46 + 2/10 = 46.2
Hence, the decimal representation of forty-six and two tenths is 46.2.
You know how to represent whole numbers and fractions on a number line. Let us represent the decimal 0.8 on the number line.
- Draw the number line.
- Divide each unit on the number line into 10 equal parts
- Write the decimal equivalent of each part
- Mark the 8th division as 0.8

As you know, decimal fractions are the fractions with denominator 10, 100, 1000, etc. Also, we can easily write the fraction with denominator 10, 100, 1000 as decimals. Now, let us take fractions which have denominator other than 10, 100, and 1000.
Consider the fraction 125 . Here the numerator is 12 and the denominator is 5. We should convert the denominator to 10, 100, or 1000. Let us convert the denominator to 10.
We already know how to make an equivalent fraction. Let us multiply both the numerator and the denominator by 2.
So, 12/5 = 12 × 2 / 5 × 2 = 24/10
24/10 = 2 + 4/10 which has 2 ones and 4 tenths. This can be written as 2.4. So, 12/5 = 2.4
Let us see how to convert decimal numbers to fractions. Consider the decimal 0.76.
Expand the given decimal as the sum of tens, ones, tenths, hundredths etc. and solve.
0.76 has no ones, 7 tenths and 6 hundredths. Let us expand the decimal as the sum of ones, tenths and hundredths.
0.76 = 0 × 1 + 7 × 1/10 + 6 × 1/100 = 7/10 + 6/100 = 76/100
This is the fractional form of 0.76. Now, simplify this fraction to its lowest form by dividing both the numerator and the denominator by its greatest common factor. Both 76 and 100 are divisible by 4. So, divide both the numerator and the denominator by 4.
76 ÷4/100 ÷4 = 19/25
Hence, 0.76 = 19/25
Let us learn, how to convert paise to rupees using decimals. We know that 100 paise = ₹1
Therefore, 1 paise = ₹1/100 = = ₹0.01
Similarly, we can express lengths and weights in decimal form as well.
For example, 1 gram = 1/1000 kg = 0.001 kg
Comparison Of Decimal Numbers
Consider the decimal numbers 0.2 and 0.06. Which is greater? As we know, we can expand the decimals as the sum of ones, tenths, and hundredths. Write the numbers in the expanded form:
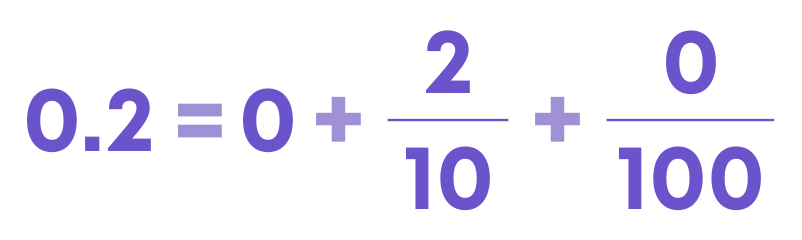

When comparing decimals, start with the whole part, then tenths place and so on. Here the whole part is the same for 0.2 and 0.06. Move to the tenths place and compare the values. Let us compare the tenths part.
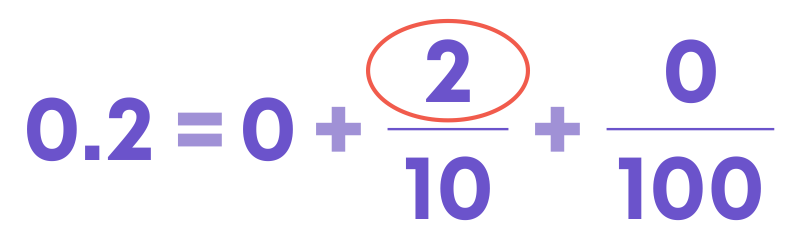
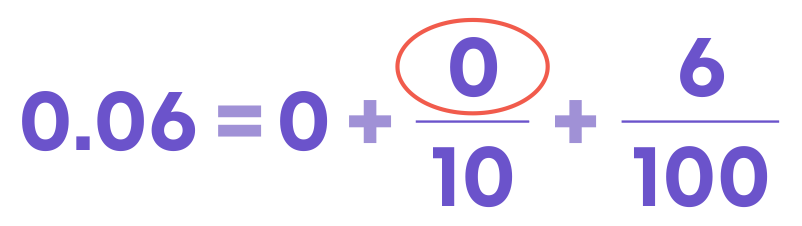
Here you can see that 0.2 has more tenths than the 0.06, i.e., 210 > 010
Hence, 0.2 > 0.06
As you know ordering decimals means arranging the values in ascending or descending order. Consider arranging the decimals 0.011, 1.001, 0.010, 0.110. We follow these steps:
Compare the whole part and each decimal place and then order them accordingly.
- Here, the whole number part of 1.001 is greater than 0.011, 0.010 and 0.110.
- The tenth part of 0.110 is greater than the tenth part of 0.011 and 0.010
So, the next greater number is 0.110
- The hundredth part of 0.011 and 0.010 are same.
- But, the thousandth part of 0.011 is greater than the thousandth part of 0.010
So, 0.011 > 0.010
Now, we can arrange the numbers in ascending and descending order.
Ascending order of the given numbers is 0.010, 0.011, 0.110, 1.010
Descending order of the given numbers is 1.010, 0.110, 0.011, 0.010
Operations On Decimal Numbers
To add decimals, we follow these steps:
- Write the decimal numbers according to their place values one below the other
- Add the decimal numbers just like the addition of whole numbers.
i.e., addition of decimals can be done by adding hundredths to hundredths, tenths to tenths, ones to ones and so on.
Consider adding the decimals 2.66 and 1.85.
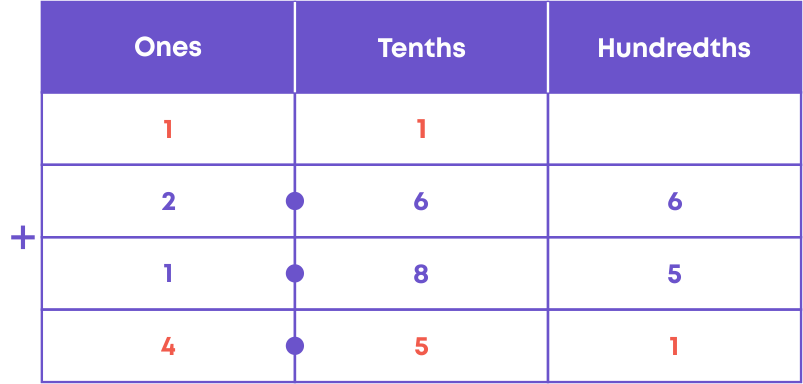
Hence, 2.66 + 1.85 = 4.51
Now let us subtract 1.87 from 2.68:
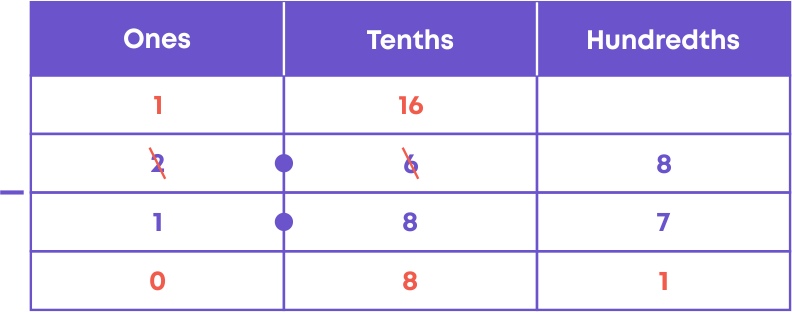
Hence, 2.68 – 1.87 = 0.81
We use the concept of decimal addition in the following scenario:
- When all the quantities are given and we have to find the total quantity
- Add the decimals to find the result
We use the concept of decimal subtraction in the following scenario:
- When the total quantity and a part of the quantity is given and we have to find the remaining quantity
- Subtract the decimals to find the result
Common Errors
The following are the topics in which students make common mistakes when dealing with decimals:
- 1. Writing the place value of the digits in the decimal
- 2. Zeroes in the decimal number
- 3. Decimal notation for money
- 4. Addition of decimals
Writing The Place Value Of The Digits In The Decimal
We can write the place value of the digit in a number by looking at the position of the digit in a number.
- The first digit after the decimal represents the tenths place, i.e., 1/10
- The next digit after the tenths place represents the hundredths place, i.e., 1/100
- The digit after the hundredths place represents thousandths place, i.e., 1/1000
For example,
- Consider the decimal number 34.268.
Here, the place value of 6 is 6100.

- Consider the decimal number 34.628.
Here, the place value of 8 is 8/1000.

Zeroes In The Decimal Number
Zeroes at the end of a decimal number written in decimal notation are not significant and therefore ignored. But the zero in the middle of a decimal number cannot be ignored. For example, consider 7.0 and 0.0003.
7.0 is the same as 7, 7.00 is the same as 7 also 7.000 is the same as 7.
0.0003 is not the same as 0.003 or 0.3, here we cannot ignore the zeroes since it depends on the place values of the digits.
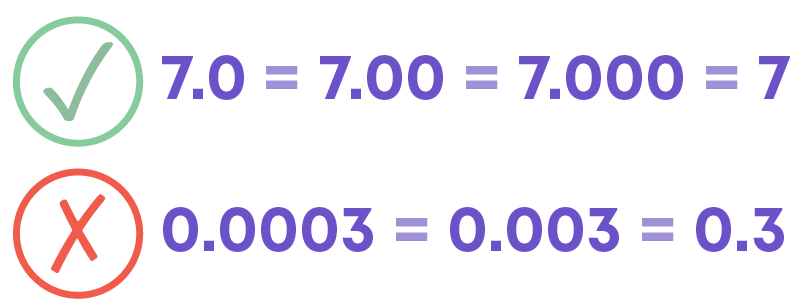
Decimal Notation For Money
To convert paise to rupees we follow these steps:
We know that 100 paise = ₹1
Therefore, 1 paise = ₹1/100.
This is nothing but 1 hundredth.
So, 1 paise = ₹1/100 = ₹0.01
For example,
- Consider 1 rupee 5 paise.
1 rupee 5 paise = ₹1 + 5 paise
= ₹1 + ₹5100
= 1 + ₹010 + ₹5100
= ₹1.05
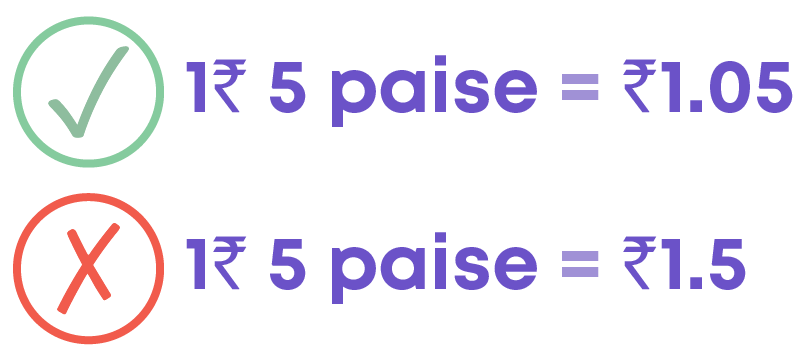
Addition Of Decimals
To add decimals, we follow these steps:
- Write the decimal numbers according to their place values, one below the other.
- Add the decimal numbers just like the addition of whole numbers.
i.e., the addition of decimals can be done by adding hundredths to hundredths, tenths to tenths, ones to ones and so on.
For example,
- Let us add decimals 0.7 and 0.5.
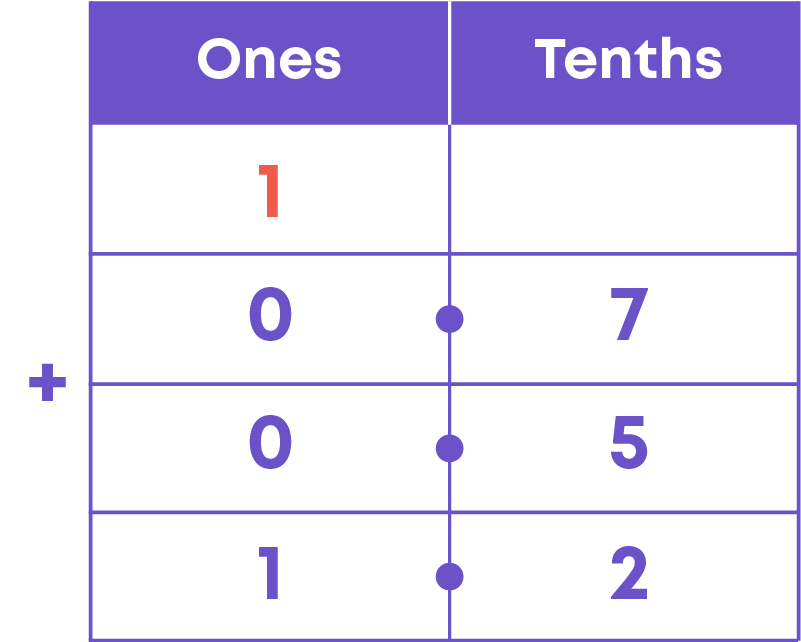
So, 0.7 + 0.5 = 1.2
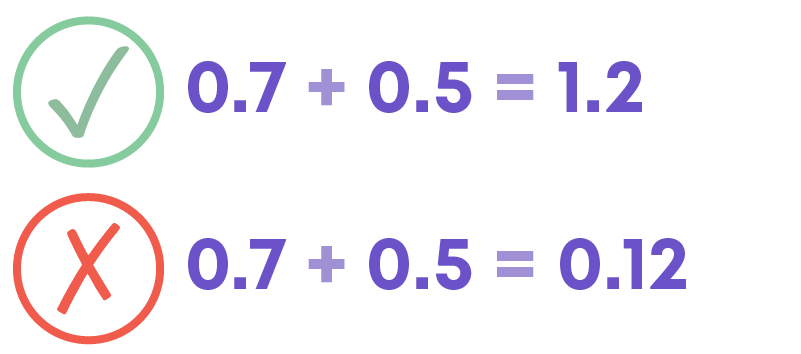
We cannot add the digits by taking the decimal point as a separator.
- Let us add the decimals, 9.9 and 12.45.
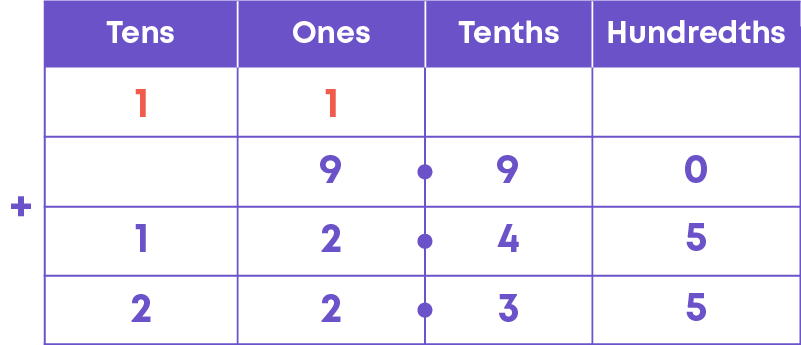
So, 9.9 + 12.45 = 22.35.
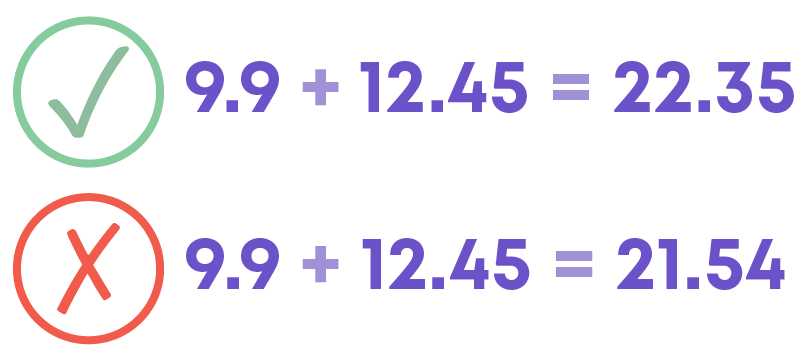
Subtraction Of Decimals
To subtract decimals, we follow these steps:
- Write the decimal numbers according to their place values one below the other.
- Subtract the decimal numbers just like the subtraction of whole numbers.
i.e., subtraction of decimals can be done by subtracting hundredths from hundredths, tenths from tenths, ones from ones and so on.
For example, let us subtract the decimals 15.6 from 24.13.
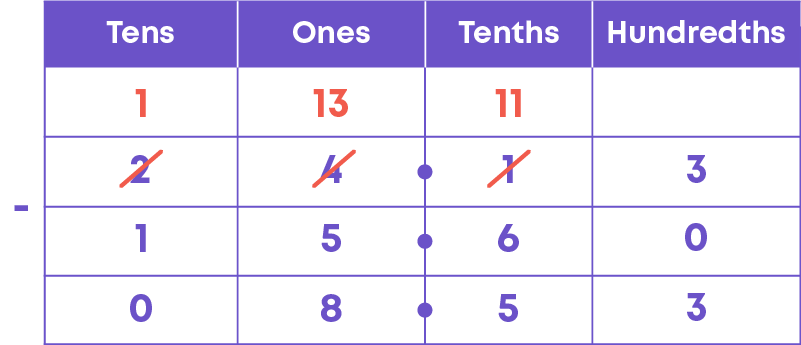
So, 24.53 – 15.6 = 8.53
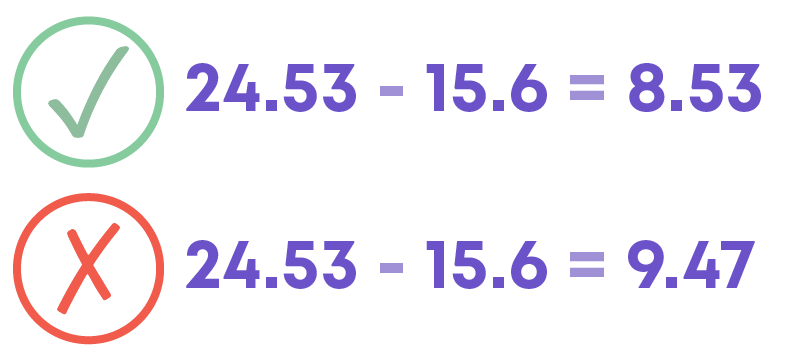
We cannot subtract the digits by taking the decimal point as a separator.
Conclusion
Can you solve this riddle based on decimals?
The number has 2 digits.
The number is less than 10.
The tenths digit is one more than the ones digit.
The digits add up to 7.
The number has 2 digits.





















































