Introduction
A branch of mathematics that talks about the length, area, or volume of different geometric shapes is called mensuration.
Geometric shapes exist in 2 dimensions and 3 dimensions. We can classify figures based on the dimensions they have. What are 2-dimensional shapes?
In geometry, a two-dimensional shape can be defined as a flat plane figure or a shape that has two dimensions – length and width.

What are 3-dimensional shapes? In geometry, a three-dimensional shape can be defined as a solid figure or an object or shape that has three dimensions – length, width and height. Unlike two-dimensional shapes, three-dimensional shapes have thickness or depth.
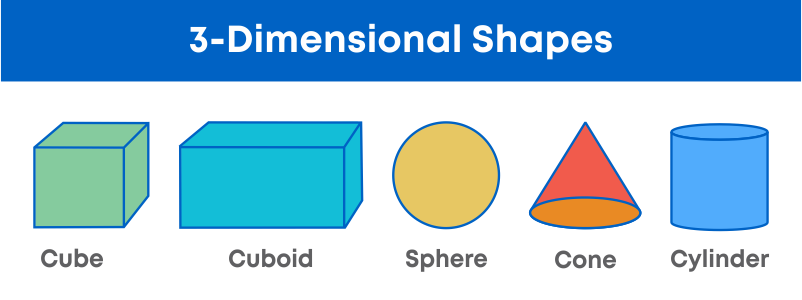
Let’s recall the differences between 2D and 3D shapes.

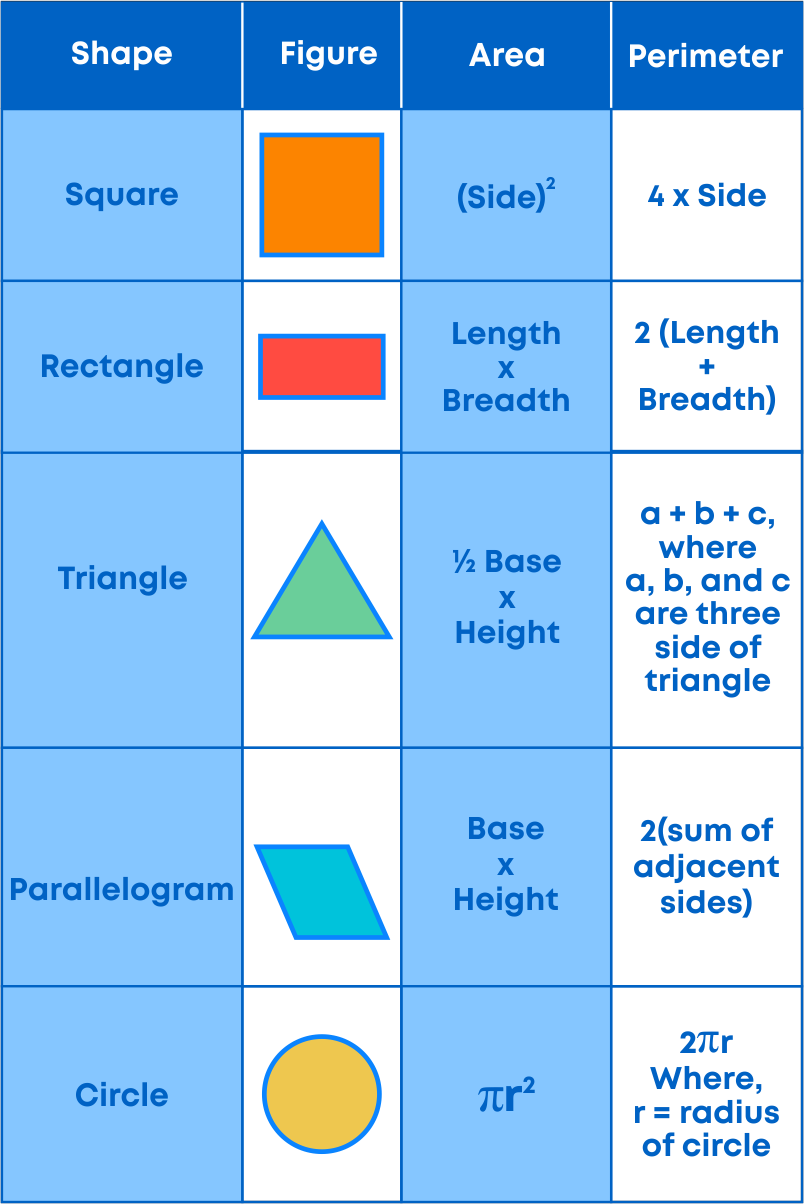
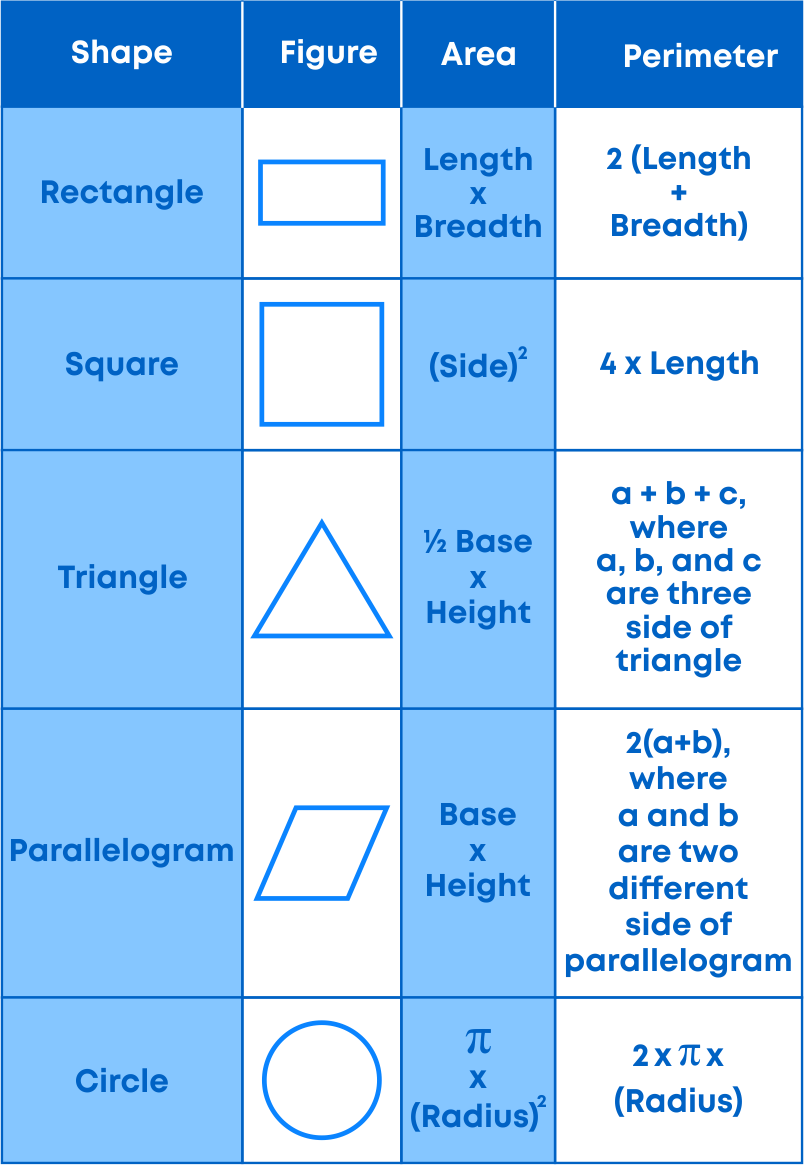
Let us revise formulas of area and perimeter of some plane figures.
We will now learn volume and surface area of solid shapes like, cube, cuboid, and cylinder. Watch the video to know more:
Remember:
- Surface area and volume are calculated for any three-dimensional shape.
- Amount of space occupied by a 3-dimensional object is called its volume.
Concepts
The chapter ‘Mensuration’ covers the following concepts:
Area and Perimeter
The perimeter can be defined as the path or the boundary that surrounds a shape. It can also be defined as the length of the outline of a shape.
The area can be defined as the space occupied by a flat shape or the surface of an object.
Below are some plane shapes and their area/perimeter:
We have learned how to find the area and perimeter of various plane figures. However, if we have the shape with a combination of two or more shapes? How do we find the area of such shapes? Let us see some examples:

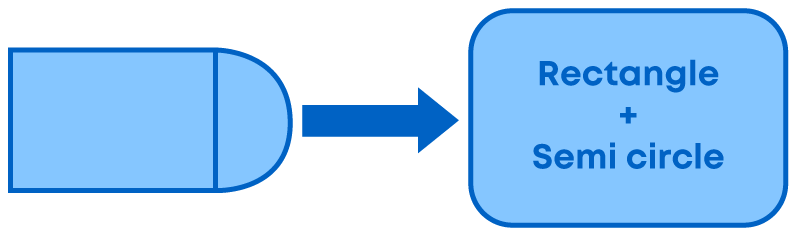
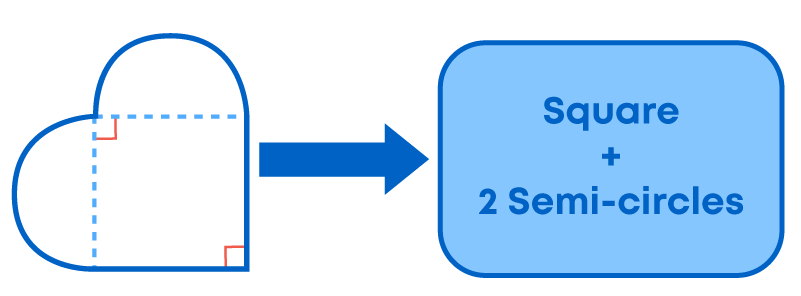
What do you notice? We see that each shape is a combination of two different shapes. To solve such problems, we use the following steps:
- Identify the different shapes which form the given shape.
- Find the area of each shape using the appropriate formula.
- Add the areas to get the area of the whole shape.
- Remember! Use appropriate units.
To solve problems on finding the area between 2 rectangles, follow the given strategy:
- Find the area of the outer rectangle and the inner rectangle.
- Subtract the area of the inner rectangle from the area of the outer rectangle to find the area between them.
Polygons
You know that a trapezium is a quadrilateral with at least one pair of parallel sides. We can calculate the area and perimeter of a trapezium using the formula
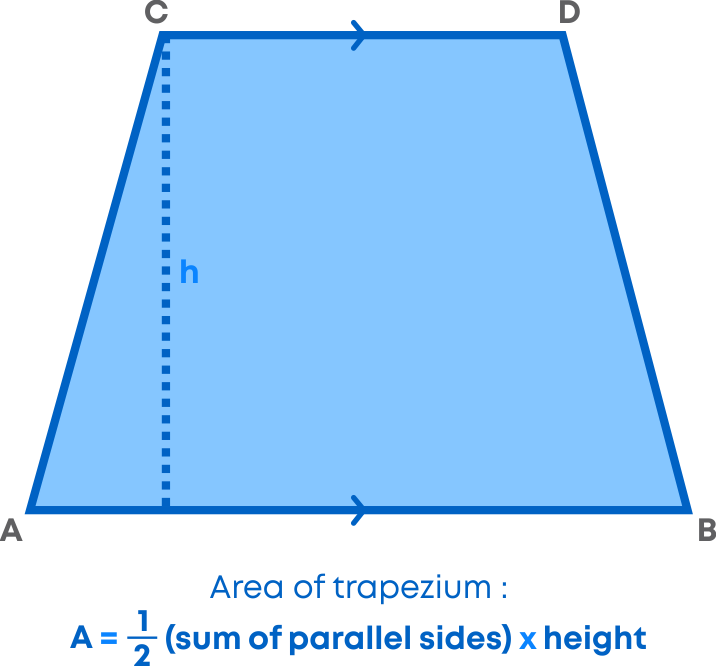
Another way to find the area of a trapezium is to divide it into two or three plane figures and then find the area.
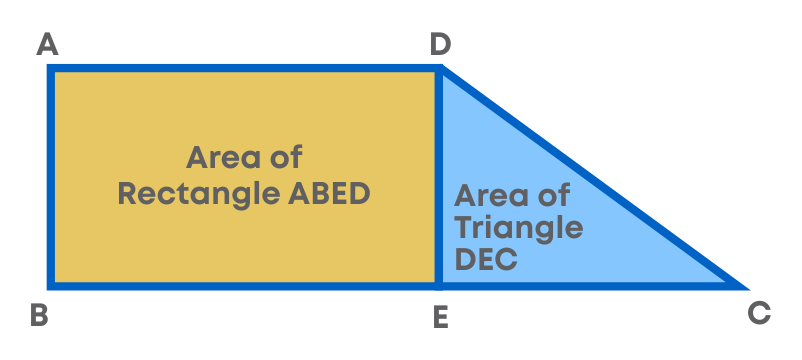
Consider the trapezium ABCD. It can be divided into two parts i.e. a rectangle and a triangle.
Area of ABCD = Area of ABED + Area of DEC
Find the area of the trapezium whose parallel sides are 6 cm and 16 cm, with a height of 5 cm. Calculate the area using both the methods.
Using the formula:
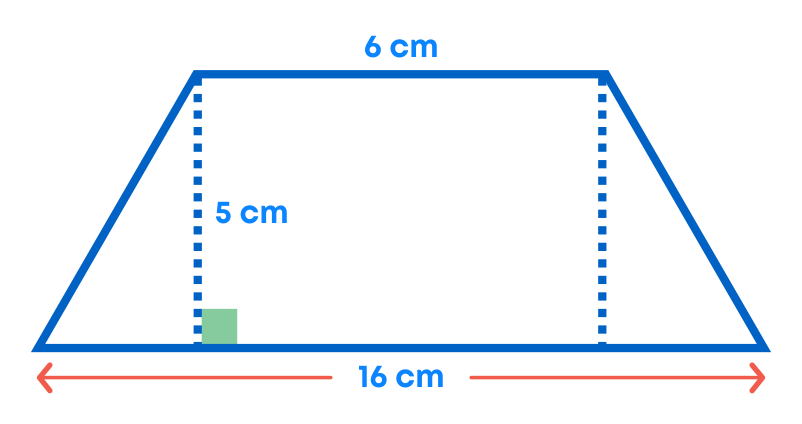
Area of Trapezium = 1 2 × sum of parallel sides × height
= 1 2 × (6 + 16) × 5
= 55 cm2
Splitting the figure:
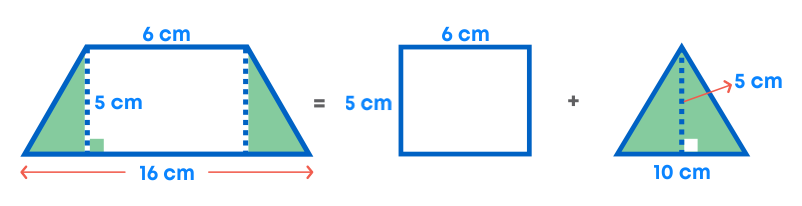
Area of the trapezium = Area of rectangle + Area of a triangle
= (6 × 5) + ( 1 2 ) × 5 × 10
= 30 + 25
= 55 cm2
Remember, trapeziums having equal area can have different perimeters.
Real-life examples of trapezium include certain tabletops, bridge supports, handbag sides and architectural elements.



Since a trapezium cannot be three-dimensional, many real-life examples of trapezium are only partly designed with that shape. For example, the surface of a table might be a trapezium, but its legs and supports are not.
- To find the height of a trapezium when the area and the parallel sides are given, use the following formula:
Height of a trapezium = area × 2 sum of the parallel sides
- To find the length of another parallel side of a trapezium, when the area, height, and length of the one parallel side are given,
The length of the other parallel side
= area × 2 sum of the parallel sides – length of the given parallel side
A general quadrilateral can be split into two triangles by drawing one of its diagonals. This “triangulation” helps us to find a formula for any general quadrilateral.
Consider a quadrilateral ABCD, with sides of different(unequal) lengths, let us derive a formula for the area of a quadrilateral.
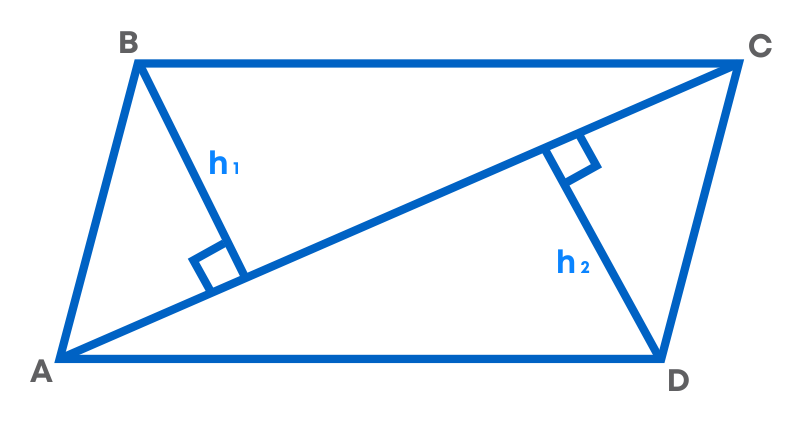
- We can view the quadrilateral as a combination of 2 triangles, with the diagonal AC being the common base.
- h1 and h2 are the heights of triangles ABC and ADC respectively.
Area of quadrilateral ABCD = (Area of ∆ ABC) + (Area of ∆ ADC)
= ( 1 2 × AC × h1) + ( 1 2 × AC × h2)
= 1 2 × AC × (h1 + h2)
= 1 2 × d × (h1 + h2)2
where d denotes the length of diagonal AC.
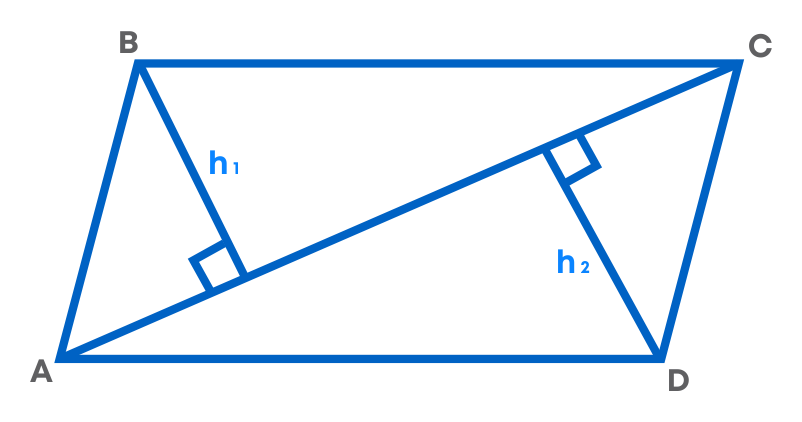
So, area of a general quadrilateral
= 1 2 × diagonal × (sum of heights of two triangles)
To find the missing diagonal in a quadrilateral, we rearrange the formula as given:
d = A × 2 h1 + h2
Rhombus is a quadrilateral whose four sides are equal, and diagonals bisect each other at right-angles. We can calculate the area of a rhombus using the formula
Area of a rhombus = 1 2 × d1 × d2
where d1 and d2 are the lengths of the diagonals.
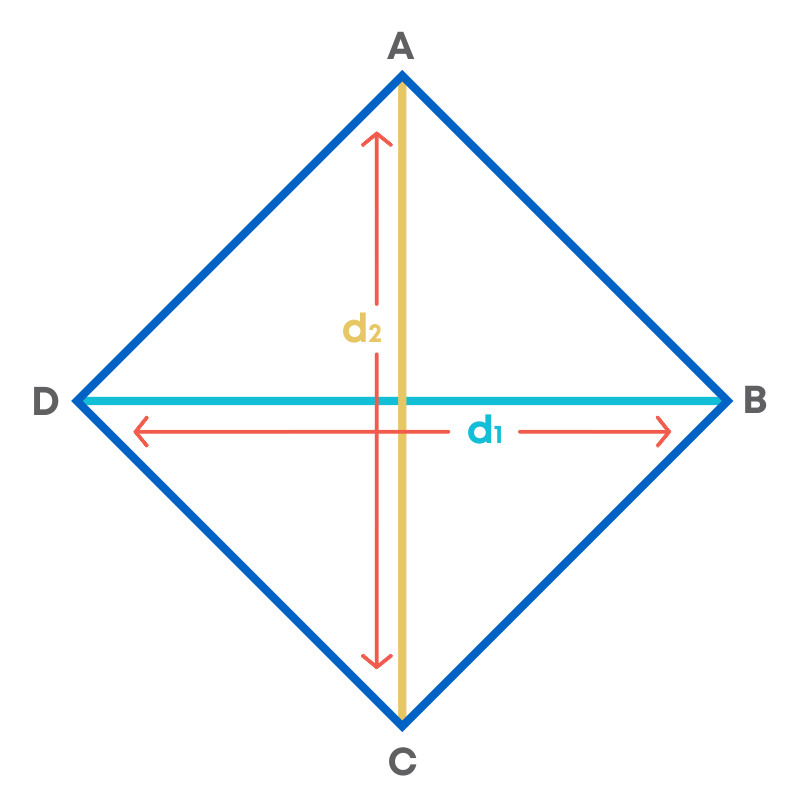
We can use the method of splitting into triangles to find a formula for the area of a rhombus. In the figure below, ABCD is a rhombus. Therefore, its diagonals are perpendicular bisectors of each other.

Area of rhombus ABCD = (area of Δ ACD) + (area of Δ ABC)
= ( 1 2 × AC × OD) + ( 1 2 × AC × OB)
= 1 2 × AC × (OD + OB)
= 1 2 AC × BD
= 1 2 × d1× d2
where AC = d1 and BD = d2
The area of a rhombus can also be calculated as base × height. Consider a rhombus ABCD, having two diagonals, i.e., AC & BD.
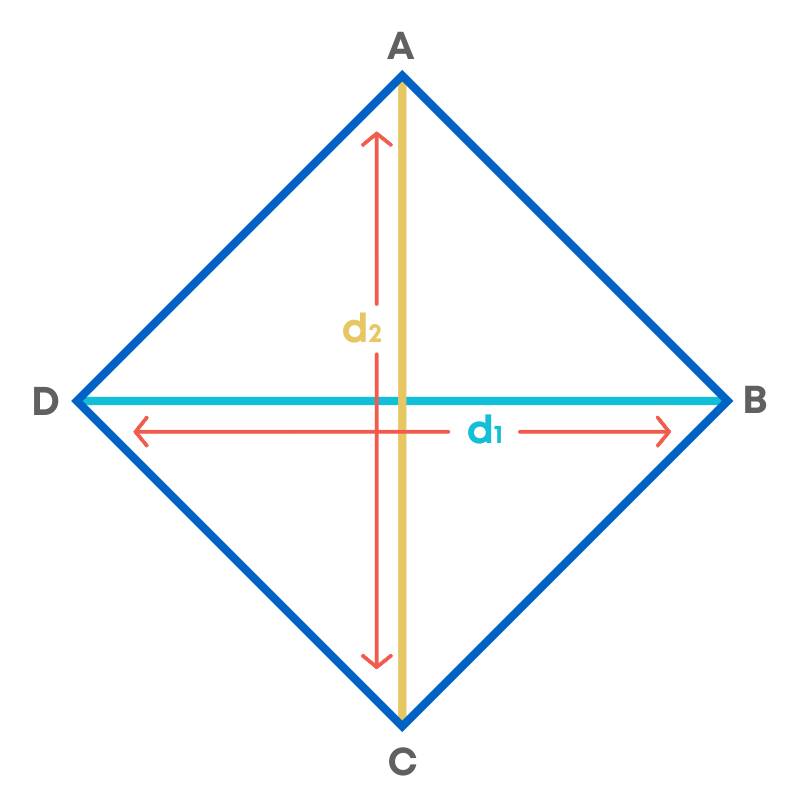
- Step 1: Find the base and the height of the rhombus. The base of the rhombus is one of its sides, and the height is the altitude which is the perpendicular distance from the chosen base to the opposite side.
- Step 2: Multiply the base and calculated height.
Let us see how to find the missing diagonal when the area is given.
We calculate the missing diagonal d1 = Area × 2 d2
Where d1 and d2 are the diagonals of the rhombus.
How do you find the area of the irregular polygon? To find the area of any polygon, we divide the polygon into triangles, rectangles, parallelogram, or trapeziums.
Why do we divide the polygon into triangles, rectangles, parallelogram, or trapeziums? We have already learnt how to calculate the area of triangles, rectangles, parallelogram, or trapeziums.
Hence, to find the area of the polygon, we divide them into triangles, rectangles, parallelogram, or trapeziums. We find the area of each shape and add all the areas to get the area of the whole polygon. For e.g., to find the area of the given polygon ABCDE:

Step 1: Let us divide the polygon into triangles and rectangle
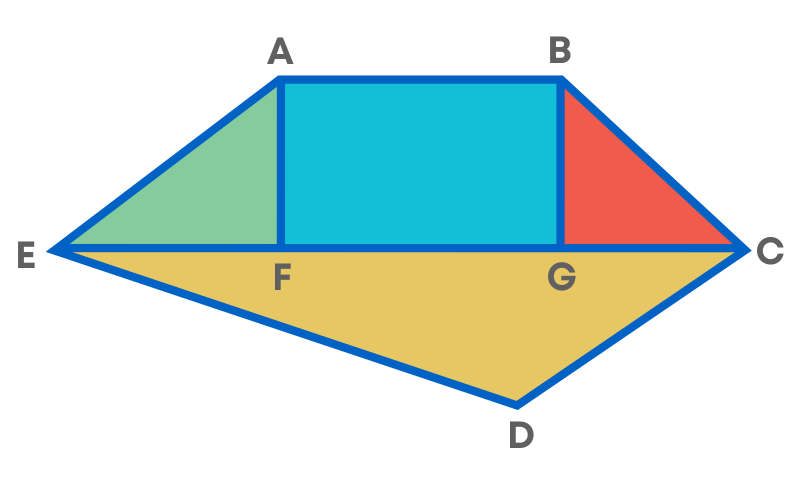
- Step 2: Find the area of each smaller shapes and add all the areas
The area of polygon ABCDE = Area of triangle AEF + Area rectangle ABFG + Area of triangle BGC + Area of triangle DEC
Do you think this is the only way to divide the polygon? No, we can divide the same polygon as
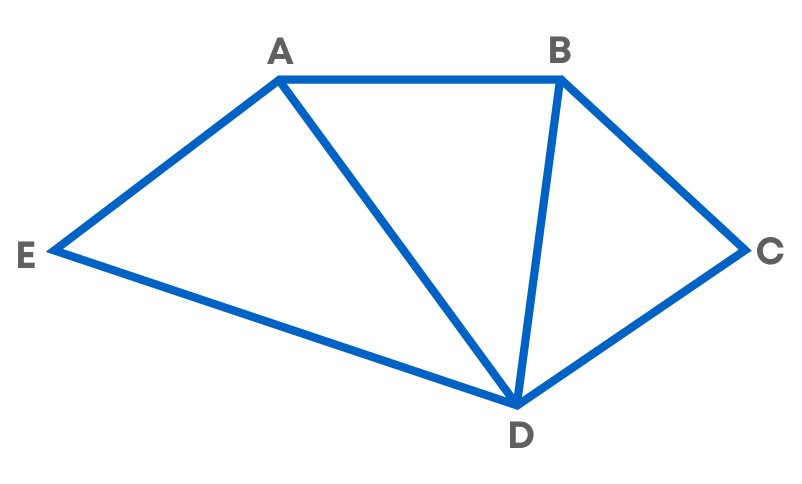
Then the area of the polygon ABCDE = Area of the triangle ABD + Area of the triangle DCB + Area of the triangle ADE
The polygon can be divided in different ways to calculate the area.
Example: Find the area of the given irregular pentagon ABCDE, in which each one of BF, CH and EG is perpendicular to AD, such that AF = 9 cm and AG = 13 cm, AH = 19 cm, AD = 24 cm, BF = 6 cm, CH = 8 cm and EG =9 cm.
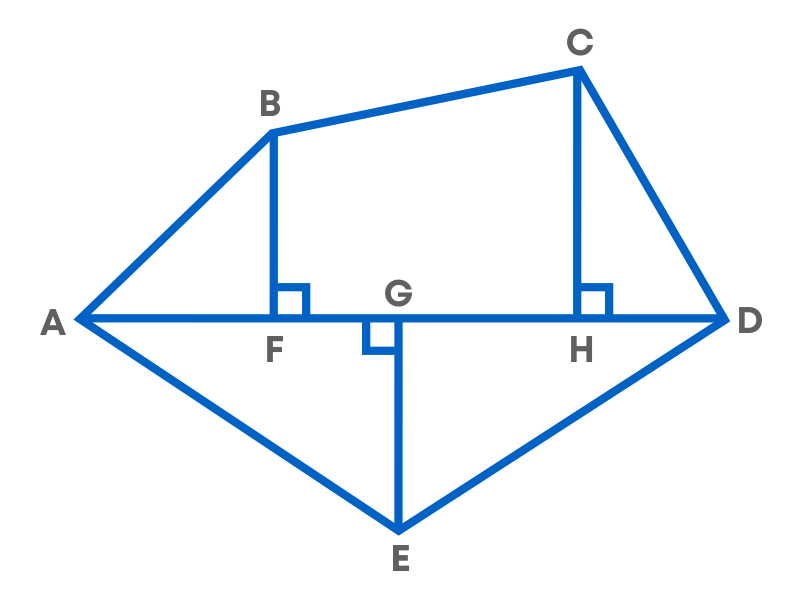
To solve, follow these steps:
Step 1: Identify each of the shapes that the polygon is divided into.
The polygon is divided into 3 triangles and a trapezium. The area of the polygon ABCDE
= Area of triangle ABF + Area of trapezium BCHF + Area of traingle CHD + Area of traingle ADE
Step 2: Calculate the areas of the different shapes that the polygon is divided into.
Area of the triangle ABF
= 1 2 × AF × BF
= 1 2 × 9 × 6
= 27 cm2
Area of the trapezium BCHF
= BF+CH 2 × FH
= 6 + 8 2 × 10
= 70 cm2
Area of the triangle CHD
= 1 2 × HD × CH
= 1 2 × 5 × 8
= 20 cm2
Area of the triangle ADE
= 1 2 × AD × EG
= 1 2 × 24 × 9
= 108 cm2
Step 3: Add the areas of all the shapes to find the area of the irregular polygon.
The area of the polygon ABCDE
= Area of triangle ABF + Area of trapezium BCHF + Area of triangle CHD + Area of triangle ADE
= 27 cm2 + 70 cm2 + 20 cm2 + 108 cm2
= 225 cm2
Let us learn how to find the area of a regular polygon using two methods:
Method 1: To calculate the area of a regular hexagon ABCDEF of side 5 cm each:
- Divide the hexagon ABCDEF into 2 trapeziums ABCF and FEDC

- We calculate the area of the trapezium and add up the area of the trapeziums to get the area of the regular hexagon.
Method 2: Now, let us divide the hexagon ABCDEF into triangle AFE and BCD and a rectangle ABDE

The area of hexagon ABCDEF = Area of ∆ AFE + Area of ∆ BCD + Area of rectangle ABDE. Let us find the area of ∆ AFE
The area of ∆ AFE
= 1 2 × base × height
= 1 2 × AE × FG
- It is given that AE = 10 cm,
- FG + HC = 13 cm – 5 cm = 8 cm
We know that ∆ AFE and ∆ BCD are congruent triangles (since AF = BC = 5 cm, FE = CD = 5 cm, and AE = BD = 10 cm). Hence, FG = HC
That is, FG = HC = 8 cm ÷ 2 cm = 4 cm
- Area of ∆ AFE
= 1 2 × AE × FG
= 1 2 × 10 × 4
= 20 cm2
- Area of ∆ BCD
= 1 2 × BD × HC
= 1 2 × 10 × 4
= 20 cm2
- Area of rectangle ABDE
= AB × BD
= 5 × 10
= 50 cm2
- The area of the hexagon ABCDEF
= 20 cm2 + 20 cm2 + 50 cm2
= 90 cm2
Let us compare the two methods:

Surface Area of Cube, Cuboid, and Cylinder
A cuboid is a three-dimensional shape with a length, width, and height.
- The cuboid shape has six sides called faces.
- Each face of a cuboid is a rectangle, and all of a cuboid's corners (called vertices) are 90-degree angles.
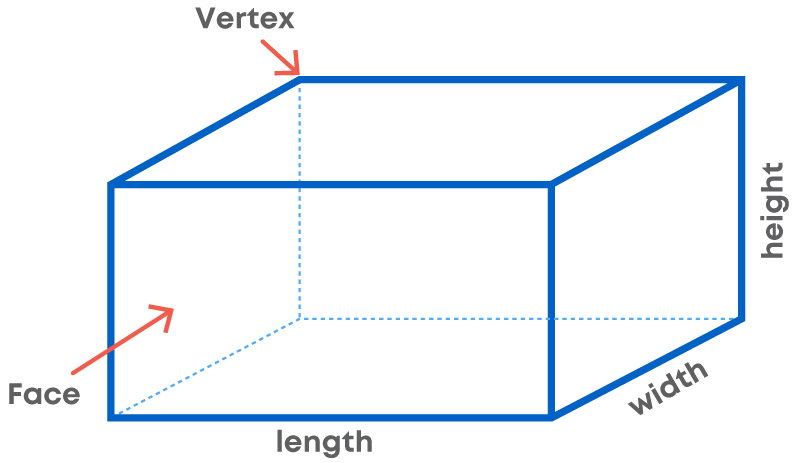
Ultimately, a cuboid has the shape of a rectangular box. If we look around, we will see so many objects which are in the shape of a cuboid, for e.g., a box or a book.
If we want to paint a cuboidal box, how would we find out the total area of all the 6 faces to be painted?
- The total area of all the faces of a cuboid is called the surface area of a cuboid.
- Total surface area of a cuboid = 2 (lb + bh + hl) (where, ‘l’ - length of the cuboid, ‘h’ - height of the cuboid, ‘b’ - breadth of the cuboid)
- The surface area of the 4 faces (or the 4 walls), excluding the base and top of a cuboid is called the lateral surface area of a cuboid.
- The lateral surface area of a cuboid = 2h (l + b)
- So, lateral surface area = Height × Perimeter of the base.
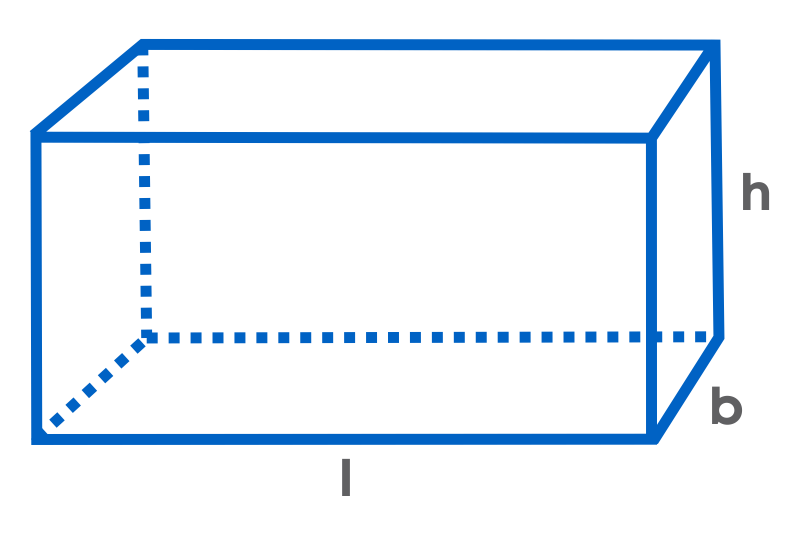
Example: The internal measures of an open cuboidal tank are 16 m × 10 m × 6 m. Find the total cost of painting all the four walls and the base of the tank if the cost of painting is ₹5 per sq. m.
In situations where we must find the cost of painting the walls and base of a cuboidal tank, follow the given strategy:
- Calculate the surface area of the 4 walls and the base of the cuboidal tank.
- To find the cost, multiply the area to be painted by the cost per unit area.
A cube is a three-dimensional shape.
- It has six faces, eight vertices, and twelve edges.
- All the faces of the cube are in square shape and have equal dimensions.

We know a cube has 6 square faces, but how do we calculate the total area of all the faces?
The total area of all the faces of a cube is called the surface area of a cube.
Total surface area of a cube = 6a2
where ‘a’ is the side of the cube
The surface area of 4 faces excluding the base and top of a cube is called lateral surface area of a cube.
Lateral surface area of a cube = 4a2
where ‘a’ is the side of the cube
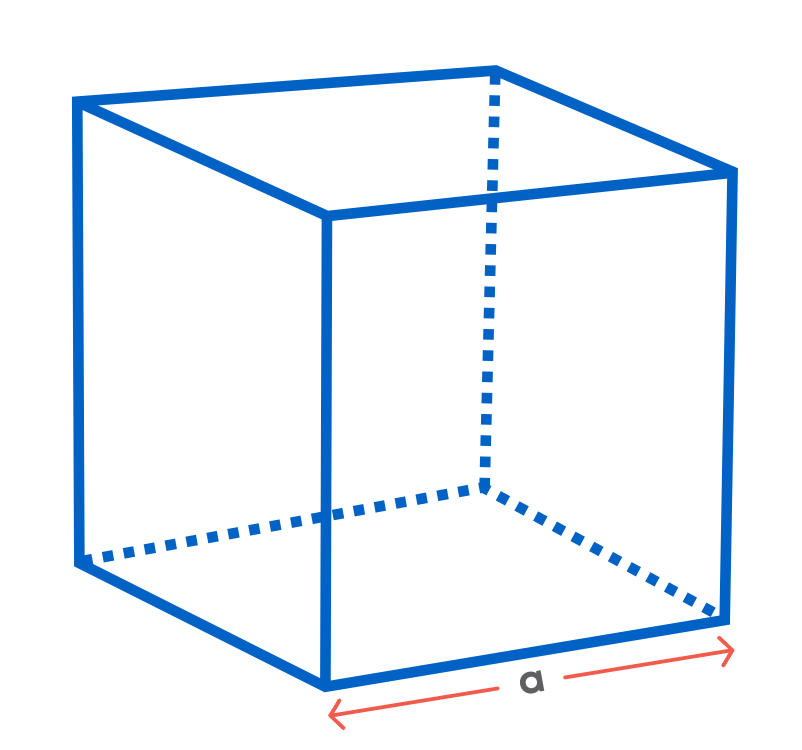
Example: The total surface area of a cubical tank is 1944 m2. Find the measure of the side of the cubical tank.
We know that total surface area of a cube = 6 × (side)2
Hence, side of the cube = √total surface area 6
= √1944 6 6
= √324
= 18
Hence, the side of the tank is 18 m.
A cylinder is a solid shape with two parallel bases generally circular in shape connected by two parallel sides.
These circular bases are always parallel and congruent to one another. A cylinder when unrolled gives a flattened look of a rectangle. Base and sides together form a cylinder.
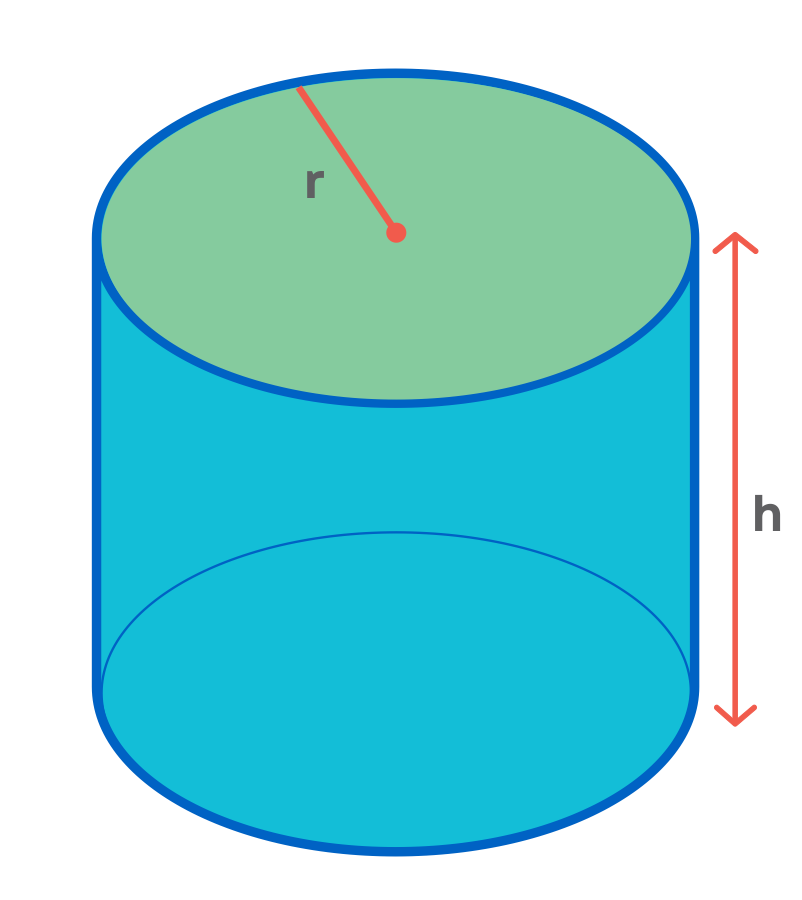
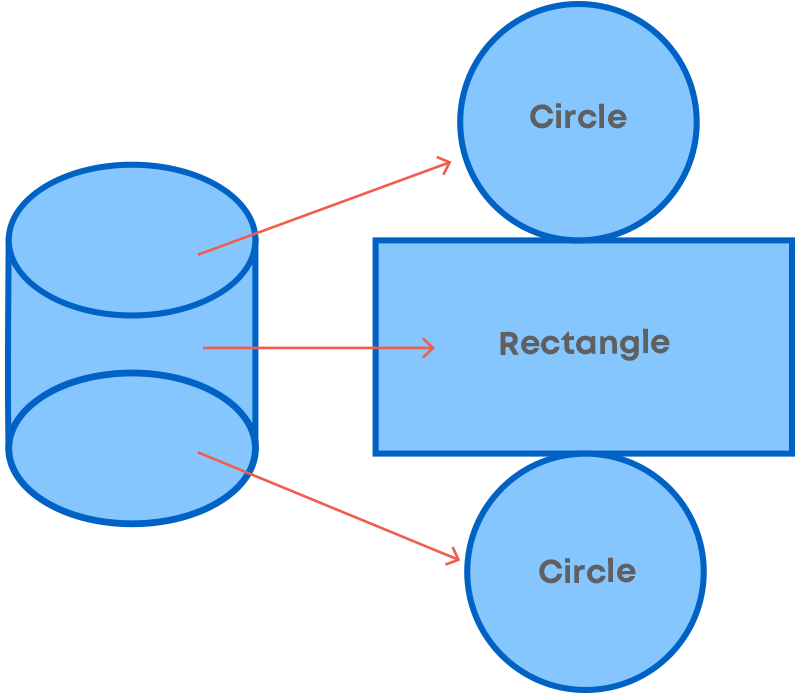
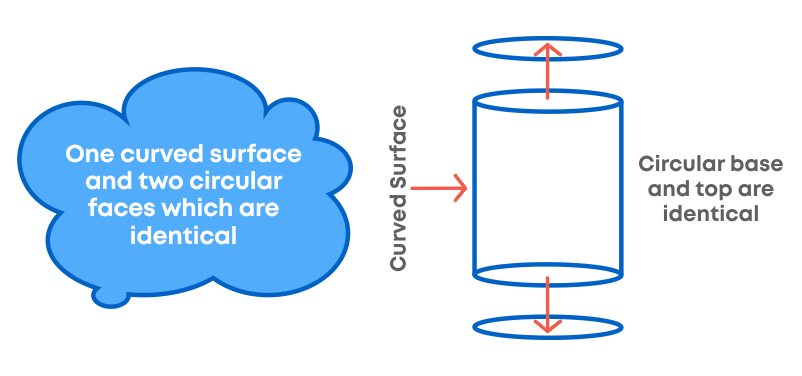
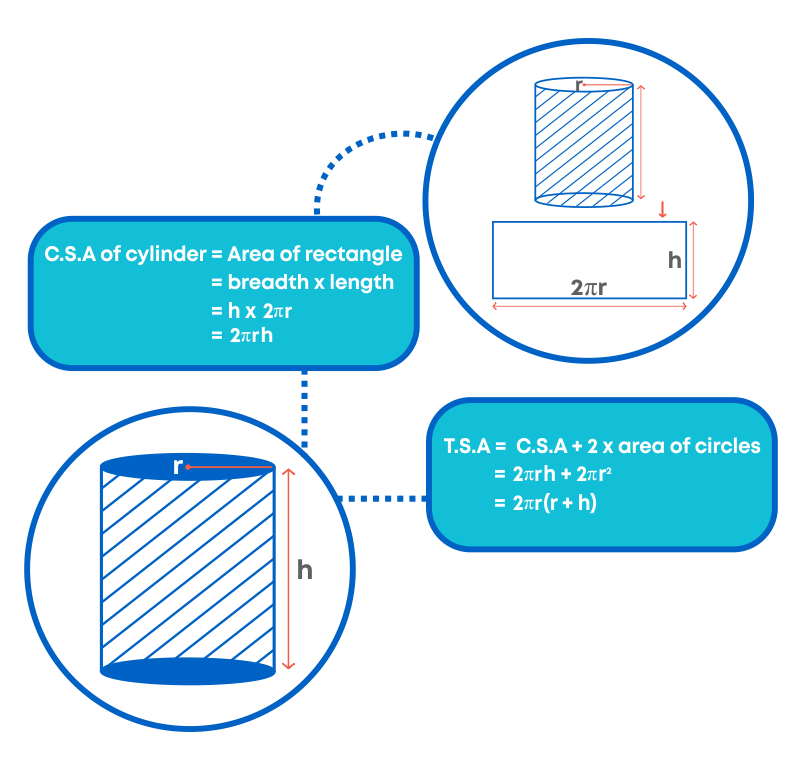
- Curved Surface Area- The curved surface area is defined as the area of only the curved surface, leaving the circular top and base. It is also termed as lateral surface area. The formula for a curved area or lateral area is given by:
CSA or LSA = 2πrh sq. units
- Base Area: The base of the cylinder is in a circular shape. Hence, by the formula of area of the circle, we know,
Area of the circular bases of cylinder = 2πr2 sq. units
- Total Surface Area- The Total surface area with radius ‘r’, and height ‘h’ is equal to the sum of the curved area and circular base areas of the cylinder.
TSA = 2πrh + 2πr2 = 2πr (h + r) sq. units
How do we find the height of the cylinder when the area is given? We will generally find two types of problems that are:
- Type 1: Find height when the curved surface area is given
- Strategy: Divide the curved surface area by 2πr
So, height = CSA 2πr
- Type 2: Find height when the total surface area is given.
- Strategy: Divide the total surface area by 2πr and then subtract the radius from it
So, height = TSA 2πr – r
Volume of Cube, Cuboid, and Cylinder
We have seen that on packets of cold drinks and milk its quantity is mentioned in ml or l.

900 ml and 2.25 litre represent the quantity of the substance and the quantity of the substance is represented by the volume.
The measurement of the total space occupied by a solid is the volume of a three-dimensional figure. Volume measures how much space an object occupies. Sometimes we might hear questions like “What is the capacity of a box?” or “How much can the box hold?” We can assume that these questions require the volume to be calculated.
Now let us understand capacity with an example:
You decide to pour a nice glass of chocolate milk! Grabbing a glass and the milk, you begin to pour - when something on TV catches your eye. You keep pouring and pouring until...splash! Milk all over the counter! What happened? You just learned about capacity or the amount a container can hold. There is a limit to how much milk will fit in your glass, and if you try to go past that limit, the milk will start to overflow!
Therefore, capacity is the maximum quantity a container can hold.
Now, try to compare the volume of objects surrounding you.
For example,
- Volume of a room is greater than the volume of an almirah kept inside it.
- Volume of your pencil box is greater than the volume of the pen and the eraser kept inside it.
Can you measure volume of either of these objects? Remember, we use square units to find the area of a region. Here we will use cubic units to find the volume of a solid, as cube is the most convenient solid shape (just as square is the most convenient shape to measure area of a region).
To find the area we divide the region into square units, similarly, to find the volume of a solid we need to divide it into cubical units.
Observe that the volume of each of the adjoining solids is 8 cubic units.

We can say that the volume of a solid is measured by counting the number of unit cubes it contains. Cubic units which we generally use to measure volume are:
1 cubic cm = 1 cm × 1 cm × 1 cm
= 1 cm3
1 cubic m = 1 m × 1 m × 1 m
= 1 m3
1 cubic mm = 1 mm × 1 mm × 1 mm
= 1 mm3
Cubic cm and litres are both metric units of volume. There may be situations where we must convert one into another. We know that 1 cm3 = 1 ml.
Therefore, 1000 cm3 = 1 l
Or 1 cm3 = 1 1000 l
The volume of the cuboid is the measure of the space occupied within a cuboid. The volume is a measure based on the dimensions of its faces, i.e., length, breadth, and height. The volume of a cuboid is given by the product of its dimensions.
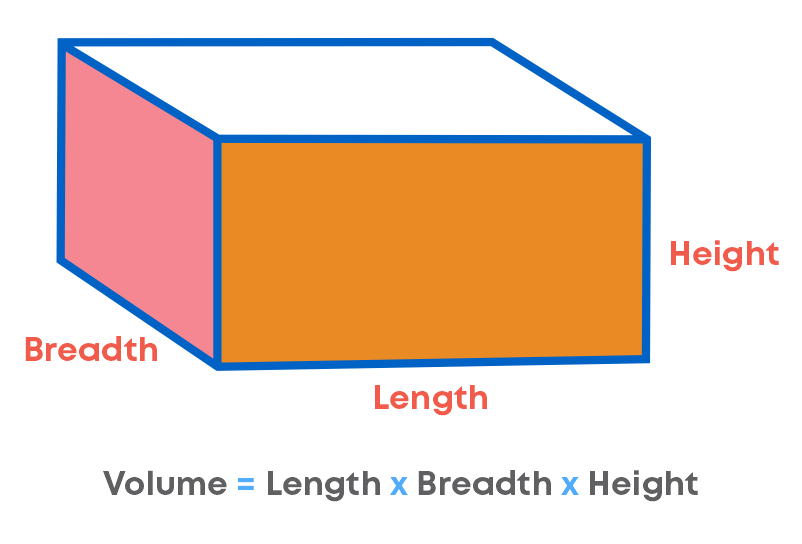
The volume of a cuboid of length ‘l’, breadth ‘b’, height ‘h’
= l × b × h cubic units
= (side)3
Let us take 36 cubes of equal size (i.e., length of sides of each cube is same). Arrange them to form a cuboid. You can arrange them in many ways. Observe the following table.
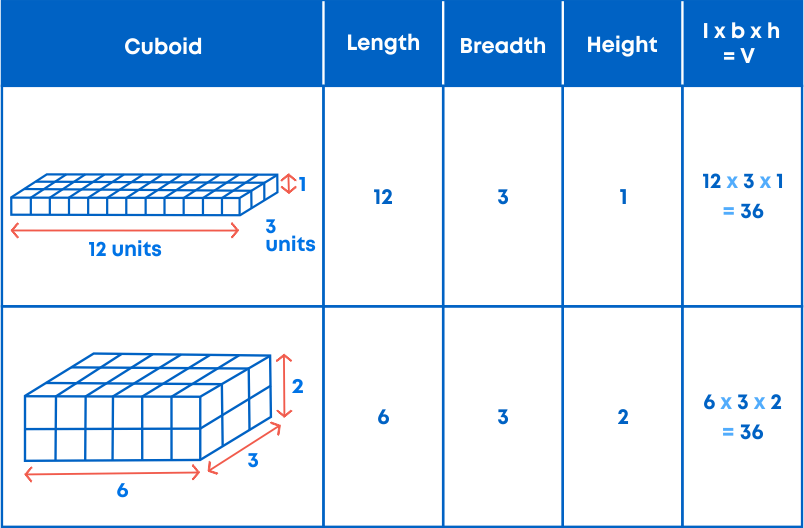
Now consider the example:
Find the height of the cuboid whose length, breadth, and volume are 35 cm, 15 cm, and 14175 cm3, respectively.
Let us first substitute the values given in the formula of volume of a cuboid = length × breadth × height
14175 = 35 × 15 × height
14175 = 525 × height
Height = 14175 525
Height = 27 cm
Therefore, height = volume length × breadth
height = volume area of the base
We can easily find the volume of a cube (V), by knowing the length of its edges. Suppose the length of the edges of the cube is ‘a’. Then the volume will be the product of length, breadth, and height. So, the formula to find the volume of a cube is:
Volume of a Cube = Length × Breadth × Height
V = a × a × a = a3
where ‘a’ is the length of the side of the cube or edges.

A cylinder can be viewed as multiple discs stacked one on top of the other. If a cylinder has radius ‘r’ and height ‘h’ then,
Volume of the cylinder = πr2h

In our daily routine, we come across different types of situations where we must handle cylindrical objects. The formula for volume of cylinder is useful in calculating the capacity or volume of such cylindrical objects. This calculation can also help in designing cylindrical containers of larger or smaller volume as per the need. For example, the designing of-
- water tanks
- perfume bottles
- cylindrical containers
- cylindrical flasks used in chemistry labs, etc.
You can easily find out the volume of a cylinder if you have the measurements of its height and radius.
Now consider this mixed problem based on surface area and volume of 3D shapes:
A metal sheet 25 cm long, 5 cm broad, and 1 cm thick is melted into a cube. The side of the cube is?
What is given in the question? Given, a metal sheet 25 cm long, 5 cm broad, and 1 cm thick.
What do we have to find? Side of the cube.
Now, since this sheet is melted to form a cube of edge length a (say), volume of the cube = Volume of the metal sheet
Then, the volume of the sheet (cuboidal)
= l × b × h
= 25 × 5 × 1
= 125 cm3
Hence, a3 = 125 cm3
So, a = 5 cm, which is the side of the cube.
Common Errors
The following are topics in which students make common mistakes when dealing with mensuration:
- 1. Relation between Volume and Capacity
- 2. Conversion of units
- 3. Area of a trapezium
- 4. Area of a polygon
- 5. Difference between Lateral surface area and Total surface area
- 6. Difference between surface area and volume
Relation Between Volume And Capacity
- Volume is the total space occupied by an object.
- Volume is measured in cubic units.
- Capacity refers to the maximum measure of an object’s ability to hold a substance, like a solid, a liquid or a gas.
- Capacity can be measured in almost every other unit, including liters, gallons, pounds, etc.
Conversion Of Units
Observe the example and the responses given below:
A water tank is in the form of a cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of water in litres that can be stored in the tank?
Response 1:

Response 2:

We know that,
1 m3 = 1000 litres, therefore, response 2 is correct.
Remember these relations:
1 L = 1000 mL
1 mL = 1 cm3
1 L = 1000 cm3
Thus, 1 m3 = 1000000 cm3 = 1000 L.
Area Of A Trapezium
Observe the example and the responses given below:
What will be the area of the trapezium given below?
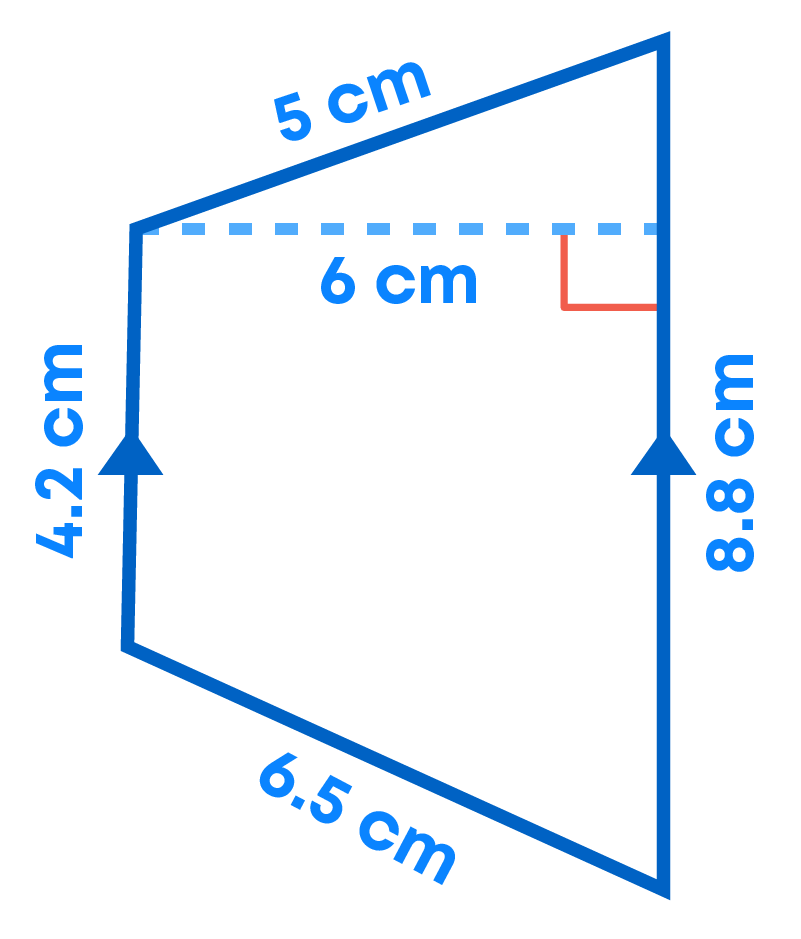
Response 1:

Response 2:
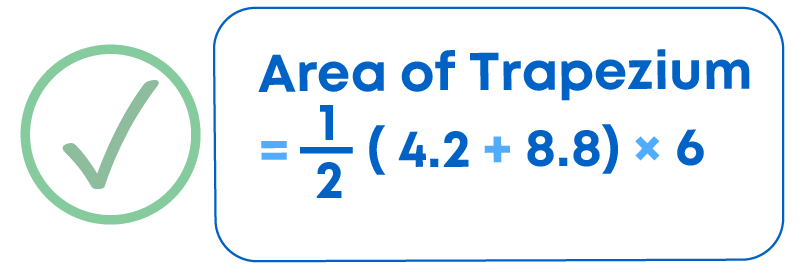
Why is response 1 wrong? It is because we have taken the sum of non-parallel sides.

Area Of A Polygon
We split a quadrilateral into triangles and find its area. Similar methods can be used to find the area of a polygon. Observe the following for a hexagon:
Divide the hexagon into parts (Triangle, trapezium, or rectangle) to find out its area.
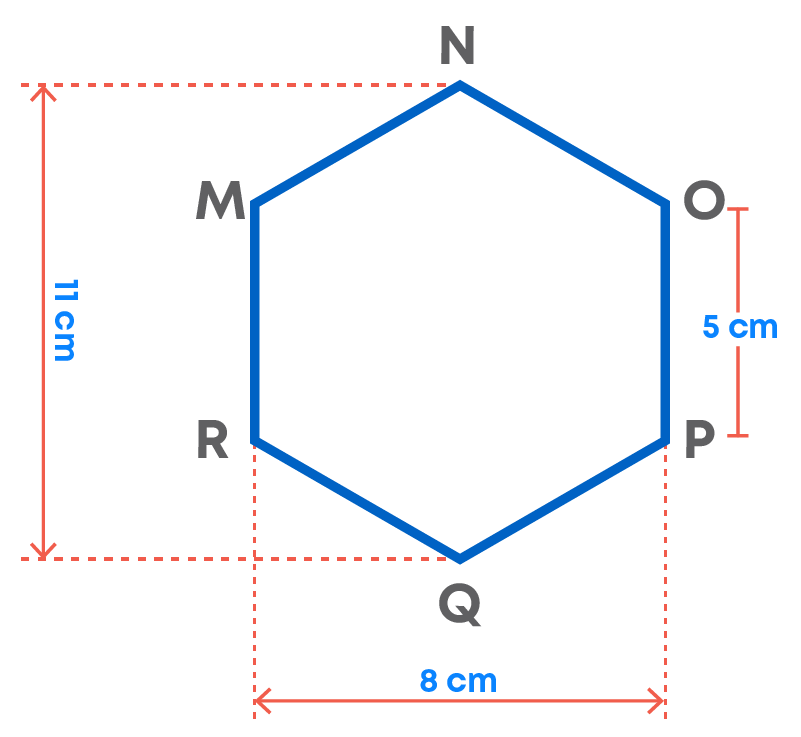
Response 1:
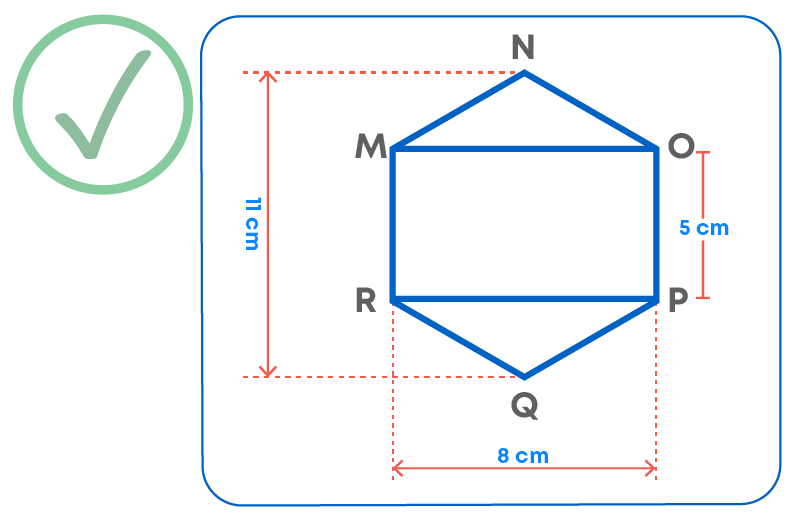
Here, we have cut the hexagon into three shapes: two congruent triangles and a rectangle. So, the total area of hexagon will be the sum of the area of two triangles and a rectangle.
Response 2:

Here, NQ divides the hexagon into two congruent trapeziums, hence, we will be able to find the area by adding the area of these two shapes.
Response 3:
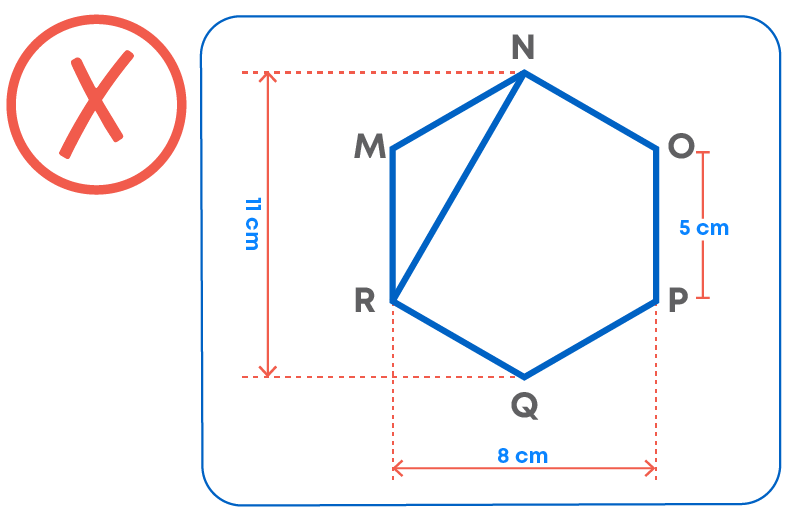
Here, we have cut the shape into one triangle and a pentagon, which is not the correct method.
Difference Between Lateral Surface Area And Total Surface Area
For shapes like cube, cuboid, and cylinder, we calculate lateral/curved surface area and total surface area. Are they the same? No, they are not!
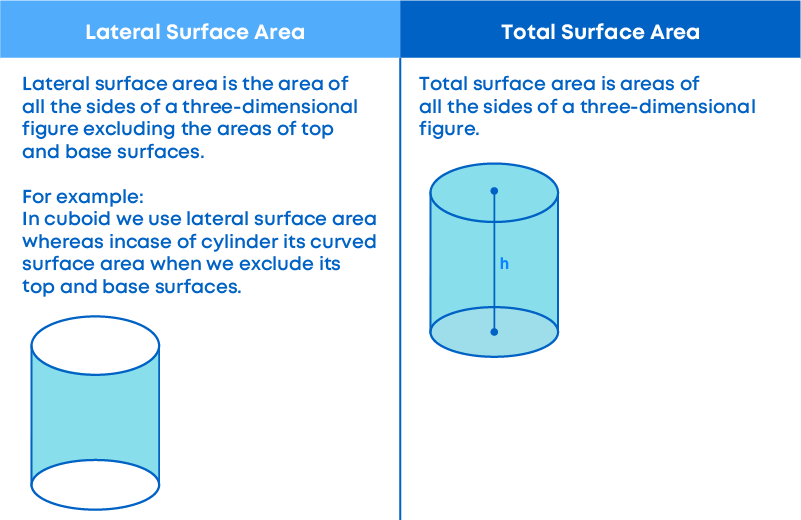
Example: Let’s say you must paint the walls of a room excluding the floor and the ceiling.
- To find out how much paint we need, we must calculate the curved surface area of the room.
- Let us say we must calculate the size of the label to be put around the curved surface of the cylindrical can. In this situation we calculate the curved surface area of the cylinder.

Example: If you must gift-wrap the cuboidal box with paper, then to calculate the amount of paper required to cover the whole box, we calculate its total surface area.

Difference Between Surface Area And Volume
Sometimes we get confused between the surface area and the volume. We know that,
Volume is defined as the space occupied by the three-dimensional object. It is measured in cubic units. For example, suppose there is a hollow bottle, so the volume is the quantity of liquid it can hold.
Surface area is the sum of the areas of all the faces of the solid figure. Finding surface area of solid figure is like finding how much wrapping paper is required to cover the solid; it is the area of the outside faces of a box. It is measured in square units.
Conclusion
Now that you have learnt mensuration, can you solve this riddle?
From a triangle, a square is removed. Find the area of the pink region.





















































