Introduction
In our daily life, there are many situations where we need to compare two quantities.
- When you want to know which is more

- When you want to know which is better

For e.g., if you want to buy a television for ₹ 20,000, you compare the features of all the televisions under ₹ 20,000 and purchase the best.
- When you want to find an increase in quantity.
For eg., to calculate the increase in the population of the country, we compare the population of the current year to the previous year.
To understand the growth of the company, we need to compare the growth from the previous years to the current year.
Comparison is used in every field. We compare quantities to understand:
- Which is more and which is less
- The right thing that is suited for a particular purpose.
Percentages are widely used to compare different quantities. Watch the video to understand the need for percentages.
Percentage is a way to express any given number as a fraction of 100, i.e., the value in each 100.
32% means 32 out of 100. We use the symbol % to represent a percentage.
Anu scored 80 marks out of 100 in the maths exam. How do we write Anu's marks? Anu’s marks can be written as 80 100.
The percentage of Anu’s marks = 80%
Concepts
The chapter ‘Comparing Quantities’ covers the following concepts:
Percentage
Two friends Reeta and Anu are discussing the marks they scored in their term exams.

Who do you think did better in the exam, Reeta or Anu? Since Reeta scored 450 marks out of 600 and Anu scored 425 marks out of 500, can we say Reeta did better? No, we cannot decide who did better just by comparing their marks. What do we do in this case? We should convert the marks into a percentage.
Per cent means per hundred.
So, we should convert the marks of Reeta and Anu per 100.
- If Reeta scored 450 out of 600, what is her score out of 100?
- If Anu scored 425 out of 500, what is her score out of 100?
By converting marks per hundred we can compare the marks and decide who did better.
Per cent is derived from the Latin word ‘per centum’ meaning ‘per hundred.’ Per cent is represented using the symbol %.
For example, 2% marks mean 2 marks out of total 100 marks. Which can be written as 2% = 2 100
In other words, percentages are numerators of fractions with denominator 100. That is, 20 100 = 20 per cent.
There are 100 children in a library. Out of the 100 children, 34 are from class 5, 26 from class 6 and 40 from class 7.
Let us find the fractions of class 5, class 6, and class 7 children.
The fraction of class 5 children = 34 100
The fraction of class 6 children = 26 100
The fraction of class 7 children = 40 100
Let us find the percentages of class 5, class 6, and class 7 children.
The percentage of class 5 children = 34%
The percentage of class 6 children = 26%
The percentage of class 7 children = 40%
Anu, Mahesh and Anish are playing in a park. Anu’s brother saw them playing. He comes and asks them a question.


All 3 of them calculate the percentage of girls in the park. Mahesh calculates as shown,

Anu calculates as shown:

Anish calculates as shown,

All of them tell Akshay that the percentage of girls is 48%.

Did you notice, all 3 of them have found the percentage in different methods? Yes! Hence, we can calculate the percentage in different methods and still arrive at the same result.
Out of the 20 balls in a basket, 15 are red in colour. Let us find the percentage of red balls in the basket. What is the fraction of red balls?
The fraction of red balls = 15 20
We need to find the percentage of red balls, that is, we need to find, out of the 100 balls how many will be red balls. Out of the 20 balls, 15 are red balls, then out of 100 balls how many will be red balls?
The percentage of red balls = 15 20 × 100
= 15 × 5
= 75%
To express a given quantity as a percentage of a whole follow this strategy.
- Express the given quantity as a fraction of the whole quantity.
- Multiply the fraction by 100.
- Put the per cent sign '%'.
Converting Fraction/ Decimal to Percentage
To compare fractional numbers, we need a common denominator. What do we do in such cases? We can convert the fractions into percentage. That is, to compare fractional numbers, we need a common denominator and we have seen that it is more convenient to compare if our denominator is 100. The maximum marks are different in both tests, in such cases if we convert the fraction into percentage, it becomes easier to compare.
Converting to percentage means: Finding how many marks out of 100.
The fraction 1625 means 16 out of 25, so let us find how many marks out of 100.
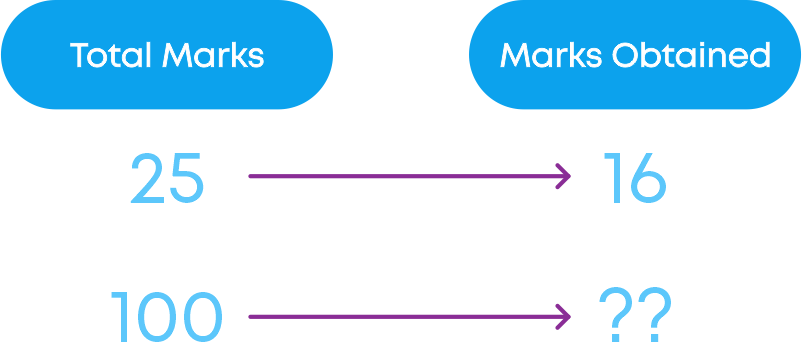
By cross multiplying, we get 16 25 × 100
= 16 × 4
= 64
That is 64 out of 100 = 64 100 = 64%
In which test did Kavita do better?
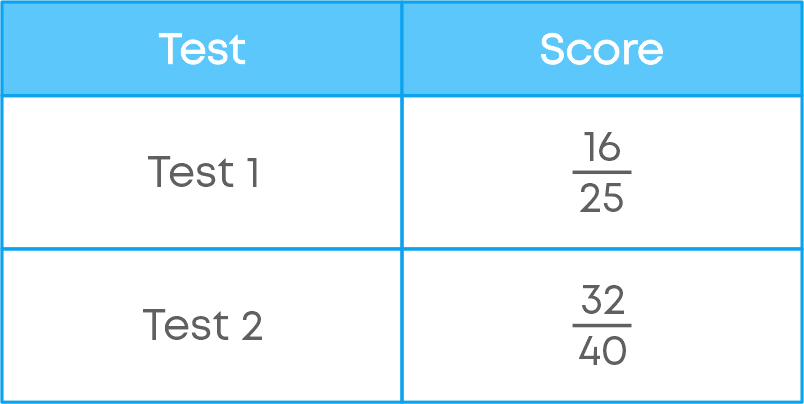
Let us convert test 2 marks into a percentage, since we already converted test 1 marks as 64%:
32 40 = ( 32 40 × 100)% = 320 4% = 80%
Hence, Kavita did better in the second test.

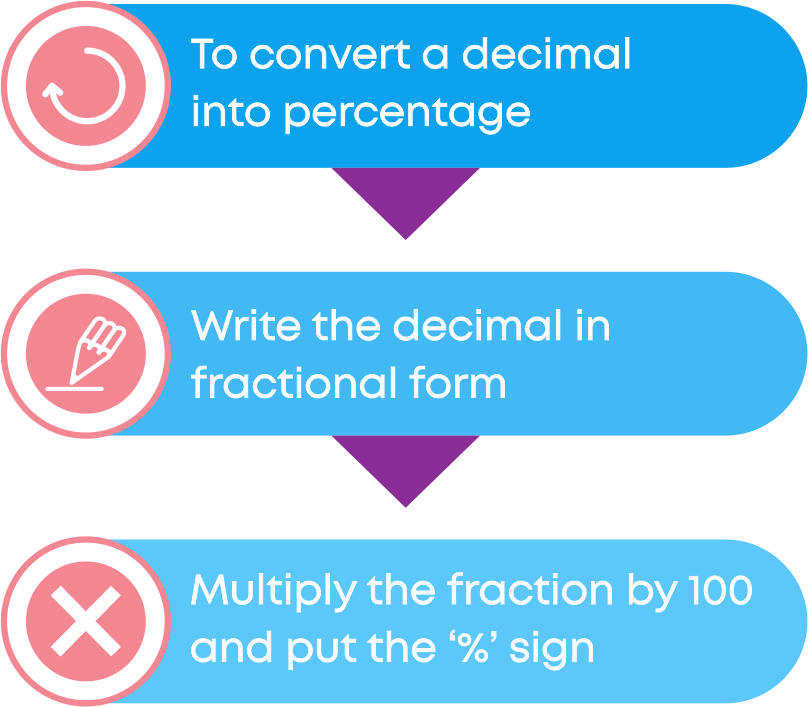
For e.g., convert 0.8 into a percentage:
0.8 = 8 10 = 8 10 × 100% = 80%
Converting Percentage to Fraction/ Decimal
We know how to convert fraction or decimal into a percentage. Now, let us understand how to convert a percentage into fraction or decimal?

Hence, 34% is equal to the fraction 17 50
Let us understand how to convert a percentage into decimal.

Hence, 22% is equal to the decimal 0.22.
To convert the percentage into a fraction:
- Divide the percentage by 100.
- Reduce the fraction to the simplest form and remove the sign %.
To convert percentage into decimal:
- Convert the percentage to a fraction by dividing the percentage by 100.
- Write the fraction in the decimal form.
Application of Percentages
Akshay goes to a shop to buy a toy. The cost of that toy is ₹600 but he has only ₹500.
Luckily, there is a sale going on in that shop. There is a discount of 25% for every purchase. Now Akshay wants to calculate the cost of the toy that he has selected, after the discount.
Do you think he has enough money to buy the toy after the discount?
Let us help Akshay find 25% of 600.
- First, write the percentage as a fraction out of 100
That is, 25% = 25 100
As you know ‘of’ means multiplication.
- Hence, multiply the fraction and the given number
25 100× 600 = 150
There will be a discount of ₹150 for the toy. So, the cost of the toy after discount is ₹600 – ₹150 = ₹450.
Hence, Akshay has enough money to buy that toy and he must pay ₹450 after applying the discount.
To find the percentage of a given quantity:
- Write the percentage as a fraction out of 100 or convert the percentage into a fraction
- Multiply the fraction by the given quantity.
You can also find the whole quantity if the percentage of the quantity is given. Let us take an example:
15% of 200 = 15 100 × 200 = 30
15% of 200 is 30 which means if 15% of the number is 30, then the number is 200. Now how do we find a number, if 15% of it is 30? Let the required number be ‘p.’ We have 15% of ‘p’ as 30.
We write 15% as 15 100
Hence, 15 100 × p = 30
p = 30 × 100 15 = 200
Hence, 15% of 200 is 30.
All the children in class 7B are eagerly waiting for their test marks. The teacher comes to the class and announces that she is going to give the marks in the form of a ratio. Neha and Ajay get their marks.
- The ratio of Neha’s mark to the total marks is 3:4.
- The ratio of Ajay’s marks to the total marks is 5:8.
By looking at the ratios can you decided who got more marks? Is it Ajay or Neha? It is not possible to say who got more marks by just looking at the ratios. To compare the ratios, we need to make the second parts of the ratios equal by taking the LCM of the second parts of both ratios. Is there any easy way to compare the marks?
Yes! If the marks are in the form of percentage, it becomes easy to compare, so here we need to convert the ratio into a percentage for easier comparison.
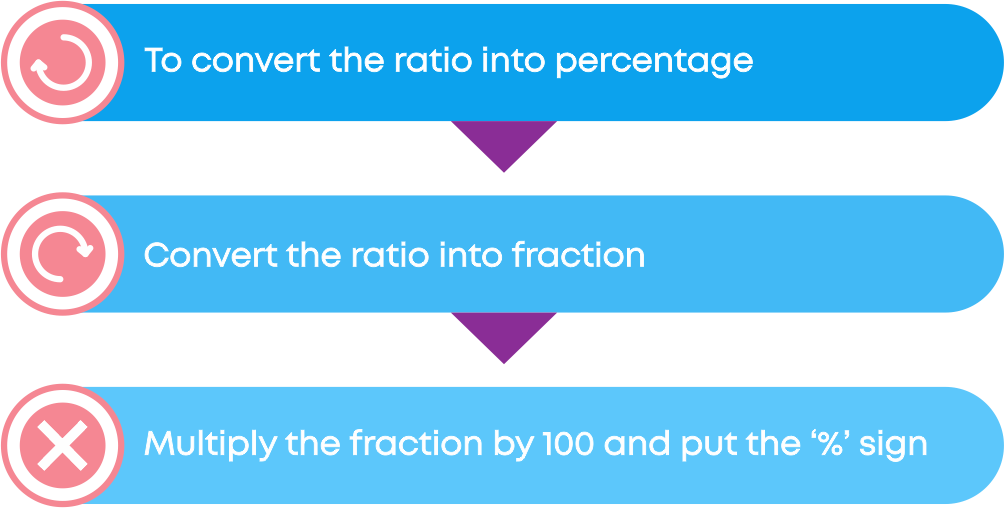
For e.g., let us convert the ratio 4:5 into a percentage:
4:5 = 4 5 = 4 5 × 100 = 4 × 20 = 80%
Anu and Vishal are supposed to pack 200 sweet boxes. The sweet boxes are divided between Anu and Vishal in the ratio 3:1. Now how do we find what percentage of the sweet box should be packed by Anu and Vishal?
Here total parts = 3 + 1 = 4
- Percentage of the sweet box that Anu must pack:
3 5 × 100 = 3 × 25 = 75%
- Percentage of the sweet box that Vishal must pack:
1 4 × 100 = 25%
To find the percentage of each part of the ratio:
- Find the fraction of each part to the total parts
- Multiply each fraction by 100 and put '%' sign
Anu had 2 pencils and her mother gave her 2 more pencils. Raghu had 4 pencils and his mother gave him 2 more pencils.

Do you think both have the same increase in the number of pencils? Yes, both got 2 pencils from their moms, hence, they had an equal increase in the number of pencils. If you see, the number of pencils that Anu had has doubled. Do you think the number of pencils that Raghu had also doubled? No! Then how can we say who received a better increase? We can compare the increase by converting it into a percentage
Can you say they both had an equal percentage of increase in the number of pencils?
Let us understand how to convert the increase or decrease in a quantity into a percentage of the initial amount.
To convert the increase or decrease into a percentage:
Percentage increase/ decrease = (amount of change / original amount × 100)%
Anu: Number of pencils increased from 2 to 4:
Here the increase in the number of pencils
= 4 - 2 = 2
Percentage increase = 2 2 × 100 = 100%
Raghu: Number of pencils increased from 4 to 6:
Here the increase in the number of pencils
= 6 - 4 = 2
Percentage increase = 24 × 100 = 50%
Hence, Anu had a better increase in the number of pencils.
Buying and Selling
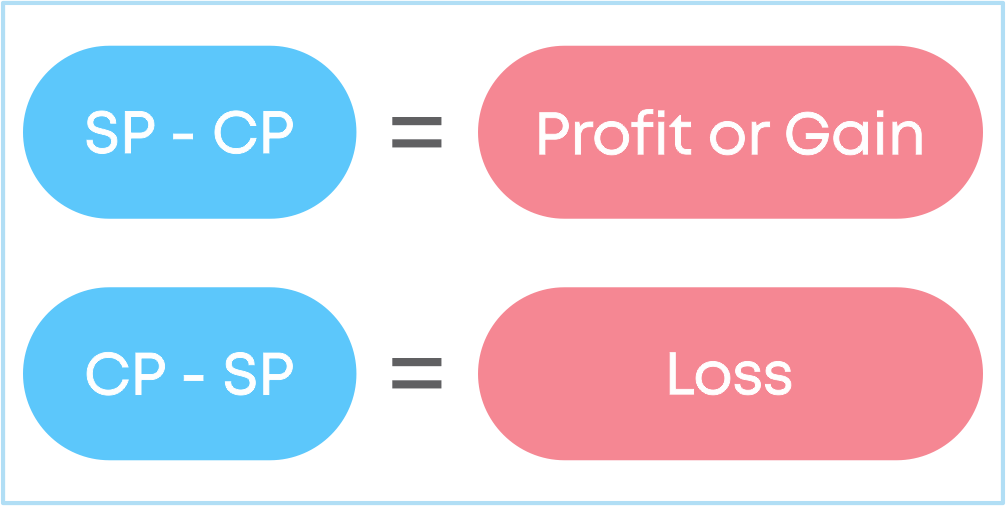
- If the buying price, that is the Cost Price (CP) is less than the Selling Price (SP), then you make a profit.
- If the buying price, that is the Cost Price (CP) is more than the Selling Price (SP), then you have made a loss.
- If the buying price, that is the Cost Price (CP) is the same as the Selling Price (SP), then you have made no profit and no loss.

- To find the profit or gain:
Selling Price – Cost Price
- To find the loss:
Cost Price – selling Price
Anu and Akshay are discussing the loss they made.

We can see that both Anu and Akshay made a loss of ₹4. Can we say both suffered the same loss? To understand who suffered more loss, we need to convert the loss into a percentage.
In general, profit and loss are expressed as a percentage. Profit and loss percentage are calculated on the cost price.
To convert loss into a percentage:
Loss % = CP-SP CP × 100
We know that: CP – SP = Loss
Hence, loss % = Loss CP × 100
In a similar way, we find the profit per cent using the formula:
Profit % = SP- CP CP × 100
We know that SP – CP = Profit
Hence, profit % = Profit CP × 100
To understand who suffered more loss, we need to convert the loss into percentage.
- Anu bought a crayon for ₹20 and made a loss of ₹4 by selling it at ₹16.
Hence, Loss % = CP-SP CP × 100
= 4 20 × 100
= 4 × 5 = 20%
Hence, Anu made a loss of 20%
- Akshay bought a book for ₹200 and made a loss of ₹4 by selling it at ₹196.
Hence, Loss % = CP-SP CP × 100
= 4 200 × 100
= 2%
Hence, Akshay made a loss of 2%.

We know how to calculate the profit% or loss% when the cost price and selling price are known. But how do we find the selling price when cost price and profit/loss% are given? Let us take an example:
The cost price is ₹250 and loss% is 12%. Find the selling price.
Given:
- The cost price = ₹250
- The loss% = 12%
Find: We need to find the selling price
We can see that the situation is loss.
Hence, Selling price = Cost price - Loss
- Let us find the loss
We know that the loss is always calculated on the cost price.
Loss = 12% of ₹250
= ₹(12 100 × 250)
= ₹30
- Let us find the selling price
Selling price = Cost price - Loss
= ₹250 - ₹30 = ₹220
Hence, the selling price is ₹220.
To find the selling price when the cost price and the profit% are given:
- Calculate the amount of profit on the cost price.
- Calculate the selling price by using the formula.
Selling price = Cost price + Profit
We know how to calculate the selling price when the profit% or loss% are known. But how do we find the cost price when the selling price and loss% are given?
To find the cost price when the selling price and loss% are given. Let us take an example:
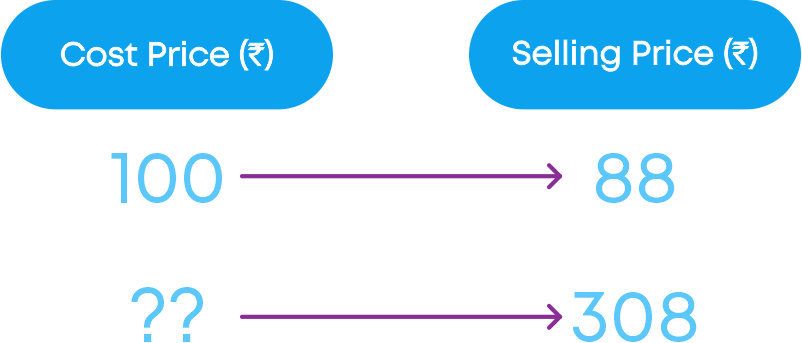
The selling price is ₹308 and loss% is 12%, find the cost price.
- The selling price = ₹308
- Loss% = 12%
We need to find the cost price.
Since the situation is loss, the selling price should be less than the cost price. We know that loss is 12% of the cost price.
- Let us take the cost price = ₹100
- Then the loss
= 12% of ₹100 = ₹12
- The selling price = Cost price – loss
= ₹100 – ₹12 = ₹88
If the cost price is ₹100, then the selling price is ₹88. Then how much is the cost price when the selling price is ₹308?
By cross multiplying we get,
The cost price
= ₹( 308 × 100 88 )
= ₹ 30800 88
= ₹350
How to find the cost price when the selling price and the loss% are known?
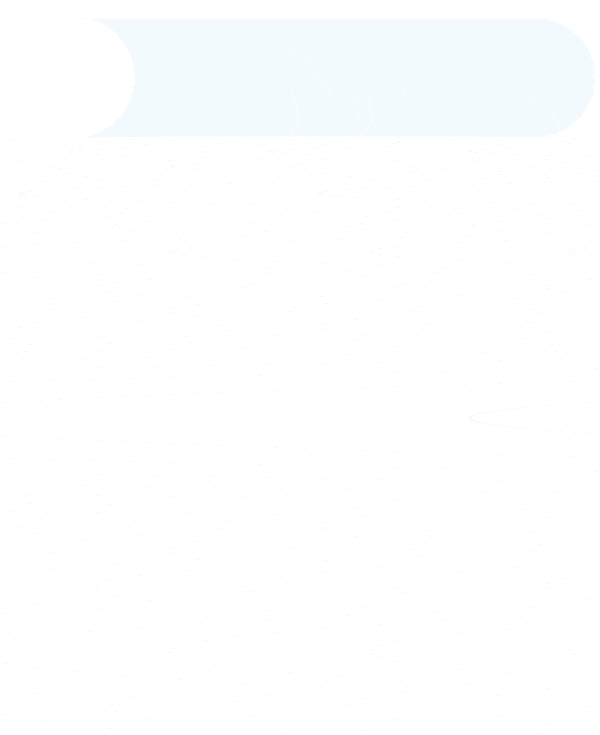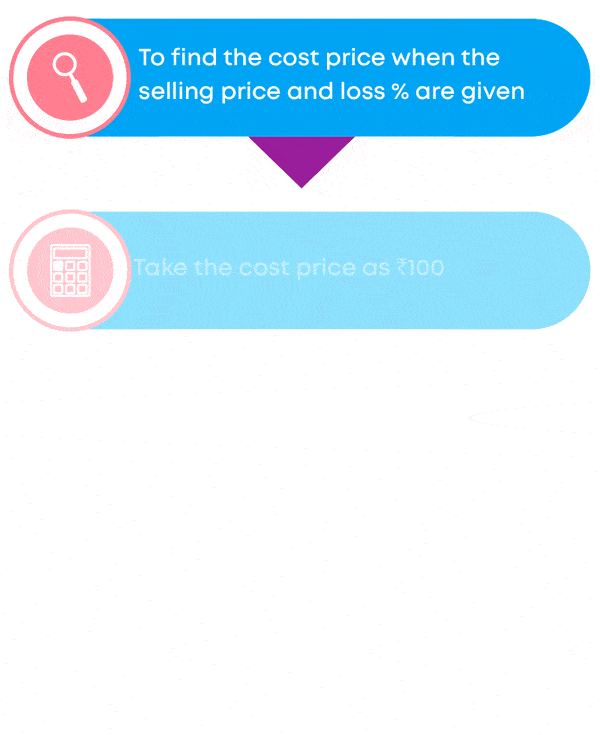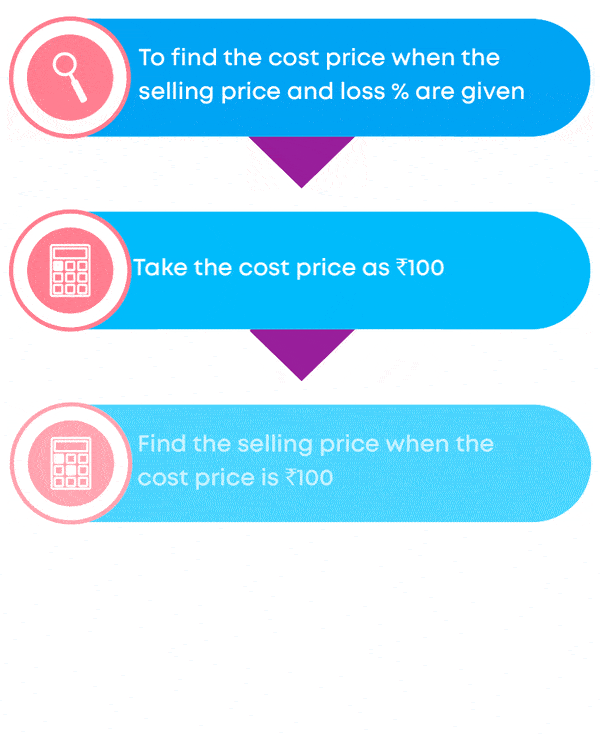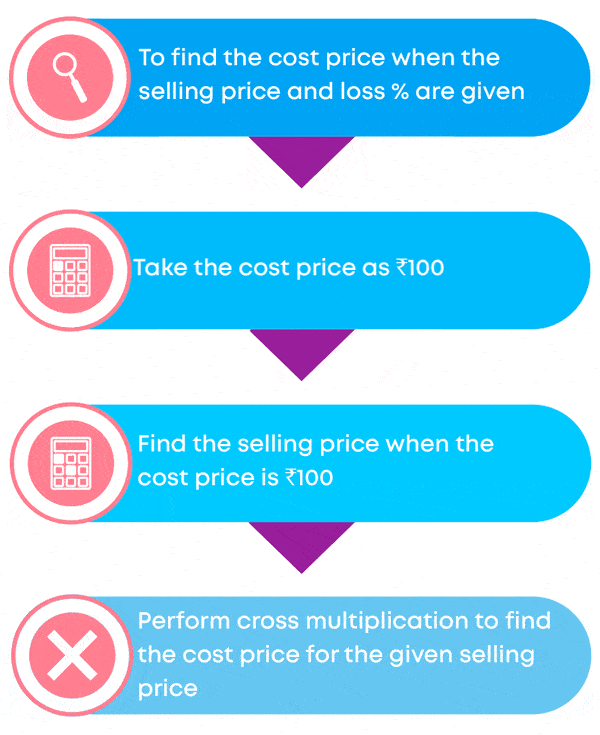
To find the cost price when the selling price and loss% are given:
- Calculate the loss on the cost price
- Calculate the Cost price using the formula
Cost price = Selling price + Loss
To find the cost price when the selling price and profit% are given:
- Take the cost price as ₹100
- Find the selling price when the cost price is ₹100
Selling price = Cost price + Profit
- Perform cross multiplication to find the cost price for the given selling price.
Simple Interest
- The money borrowed from a bank is called the principal or the sum.
- To the borrowed money at the end, we need to pay an extra amount that is called interest.
- The total money paid by the borrower at the end is called the amount.
Amount = Principal + Interest - Interest is calculated as the percentage for a period of one year that is per annum. Interest on ₹100 for 1 year is known as the rate per cent per annum.
Now, what is simple interest? The interest-based only on the principal amount is called simple interest. In short, we write simple interest as SI. For e.g., if you have taken a loan of ₹12,000 from a bank, to keep this money for two years, you must pay ₹1,000 for the first year and ₹1,000 for the second year. ₹2,000 is called simple interest.
If the money borrowed is ₹2,000 and the interest is 10% per annum:
Then the interest that must be paid for one year is 10% of ₹2,000.
- Let us calculate 10% of ₹2,000
10% of ₹2000 = ₹( 10 100 ×2000)
= ₹(10 × 20) = ₹200
Hence, ₹200 is the simple interest to be paid for the principal ₹2,000 for one year.

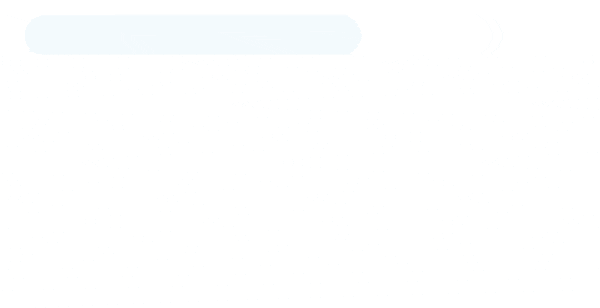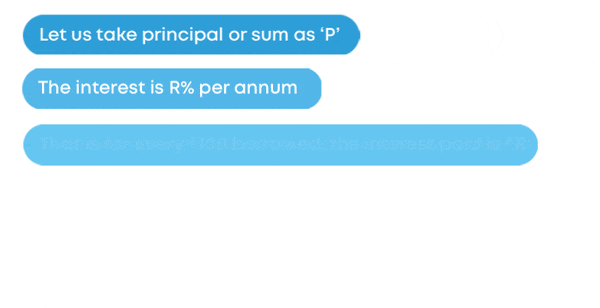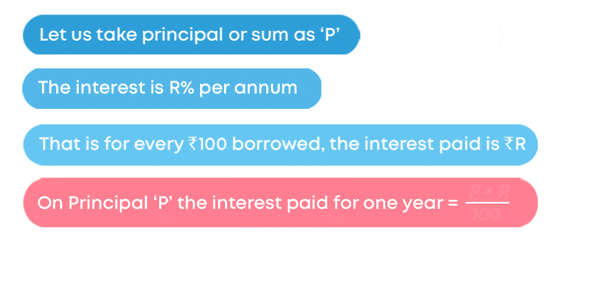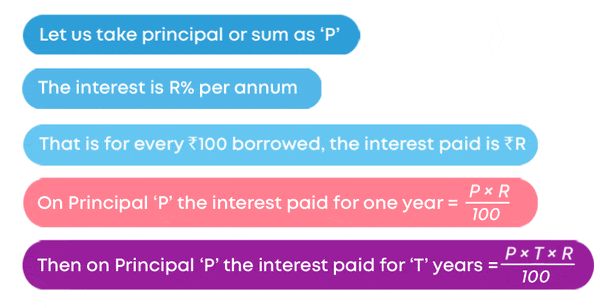
To find the simple interest/amount to be paid on a given sum of money for more than one year:
We calculate the simple interest using the formula,
SI = P × R × T 100 100
Where P is principal, R is the rate of interest, T is time period.
To calculate the amount, we use the following formula,
How do we calculate if the principal, the time, and the rate of interest are given?

How do we calculate if the rate of interest, when the time period, SI and principal are given?

How do we calculate if the time period, when the principal, SI and the rate of interest are given?
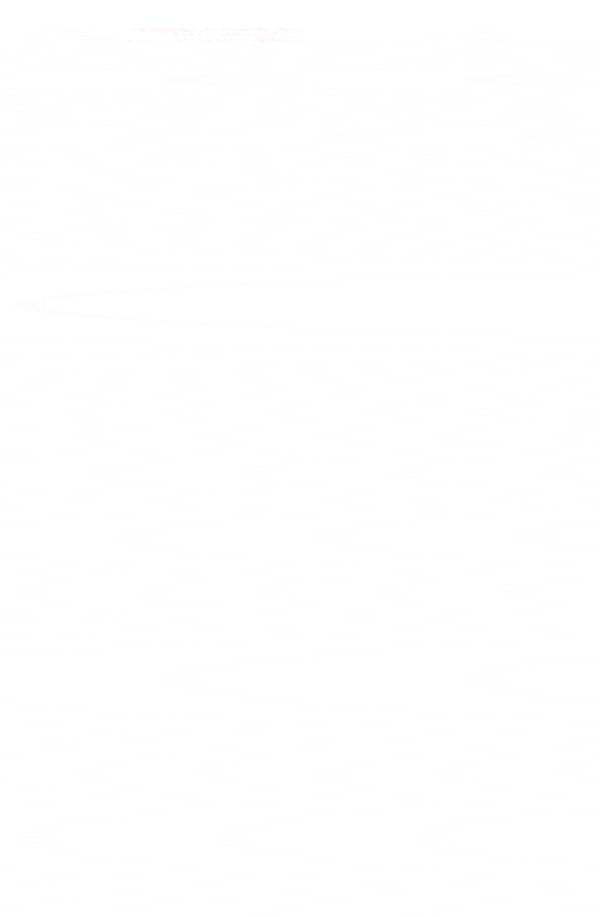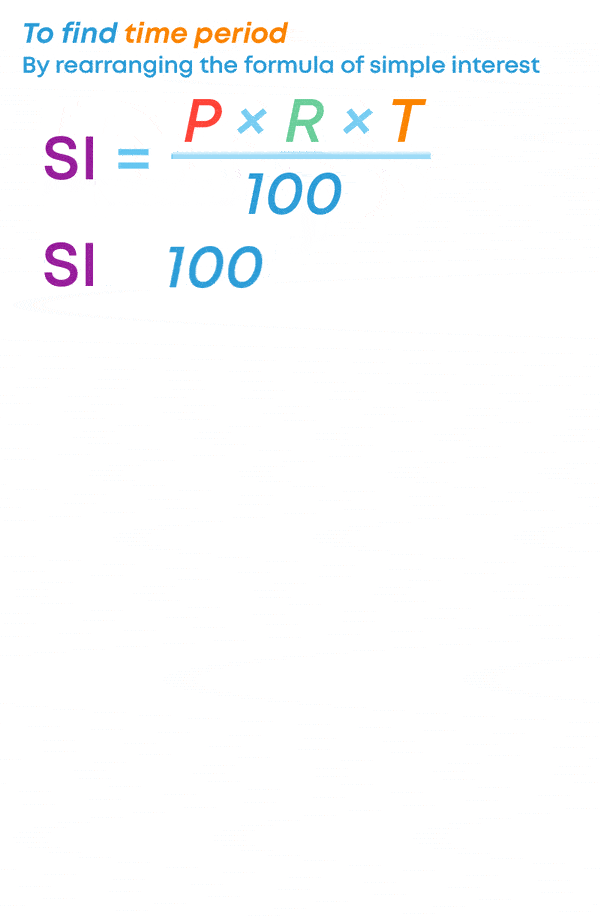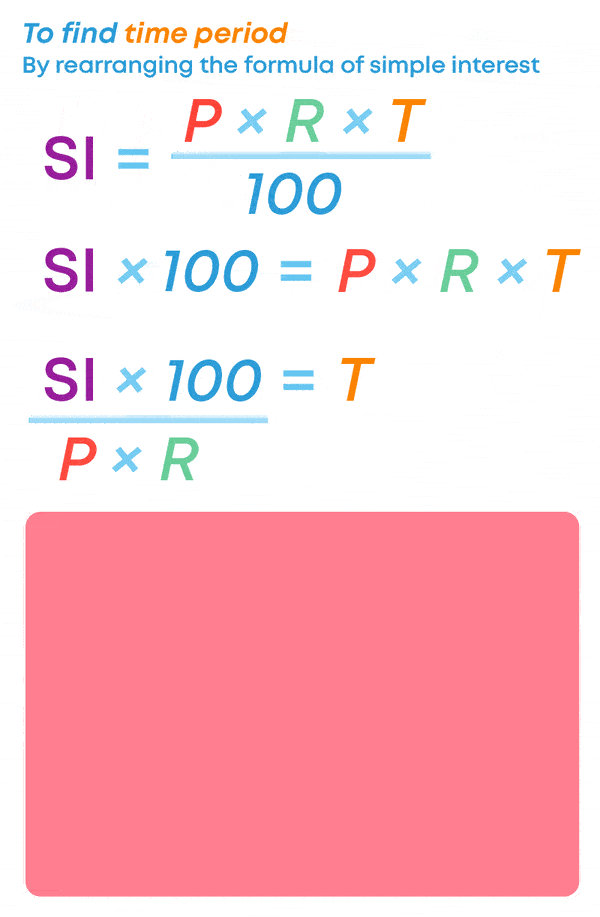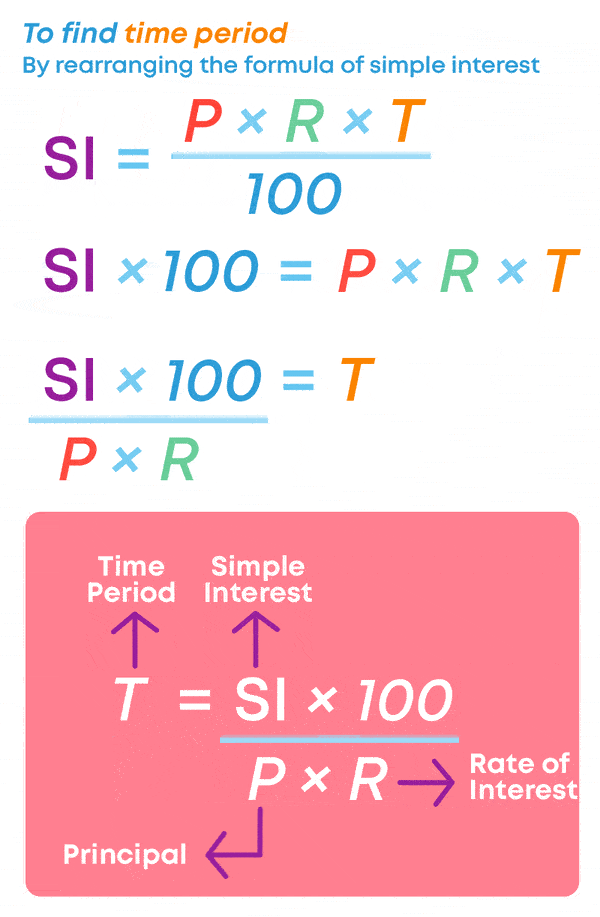
Common Errors
The following are topics in which students make common mistakes when dealing with comparing quantities:
- 1. Percentage means out of 100
- 2. Profit and Loss
- 3. Profit or loss percentage is always calculated on the cost price
- 4. Increase or decrease percentage is always calculated on the original price
- 5. How to calculate simple interest when the time period is in the form of months?
Percentage Means Out Of 100
To find what per cent of 500 is 20
- Correct method: 20 500 × 100
- Incorrect method: 20 100 × 500
To find 20% of 500:
- Correct method: 20 100 × 500
- Incorrect method: 20 500 × 100
Profit and Loss
- When the selling price is more than the cost price the situation is profit.
- When the selling price is less than the cost price the situation is a loss.


Profit Or Loss Percentage Is Always Calculated On The Cost Price
We calculate the profit or loss percentage on the cost price of an item, not the selling price. For e.g., The shopkeeper buys a shirt for ₹200 and sell it for ₹250. Here the situation is profit.
Profit = Cost price – Selling price = ₹250 - ₹200 = ₹50. Now,

Increase Or Decrease Percentage Is Always Calculated On The Original Price
We calculate the increase or decrease percentage on the original price of an item, not the increased /decreased price.
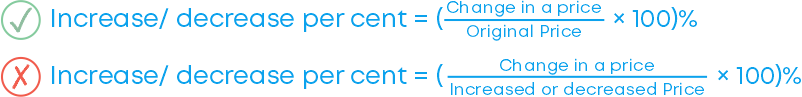
How To Calculate Simple Interest When The Time Period Is In The Form Of Months?
To calculate simple interest when the time period is in the form of months, first, we need to convert the months to years and then use the formula to find the simple interest. For e.g., Principal P = ₹2,000, Rate of interest R = 8% and Time period T = 9 months We need to convert 9 months to years.
9 months = 9 12 years
Then,
Simple Interest = P × T × R 100
= 2000 × 9 × 8 100 × 12
Conclusion
We compare quantities almost daily in our lives. Something as simple as ordering food involves comparing quantities, as you compare different restaurants for food options, customer reviews, prices, etc. and then make your choice. Can you solve the riddle below based on comparing quantities?
What percentage of the figure is coloured?





















































