Cube Numbers

You know that the cube of 2 can be written as 2 multiplied by itself three times, i.e.,

In other words, a cube of a number is obtained when a number is multiplied by itself three times. Consider the number 64. When you multiply 4 with 4 three times, the product is 64. Hence, 64 is the cube of 4.

Similarly,1 × 1 × 1 = 1

2 × 2 × 2 = 8

3 × 3 × 3 = 27

4 × 4 × 4 = 64 and so on.

The numbers 1, 8, 27, 64 ... are called cube numbers. These numbers are also called as perfect cube numbers.

When a number is multiplied by itself three times, the product is called a cube number. E.g.:

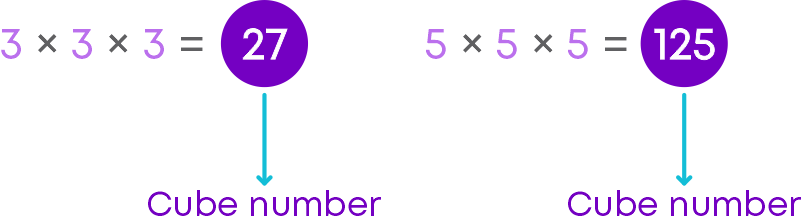
The cube numbers from 1 to 1000 are:

There are only 10 perfect cubes from 1 to 1000. Also, from the table above, you can see that cube of a 1–digit number is a 1-digit or 2-digit or 3-digit number.

Now, let us take odd numbers 1, 3, 5, 7 and 9 and their cubes.

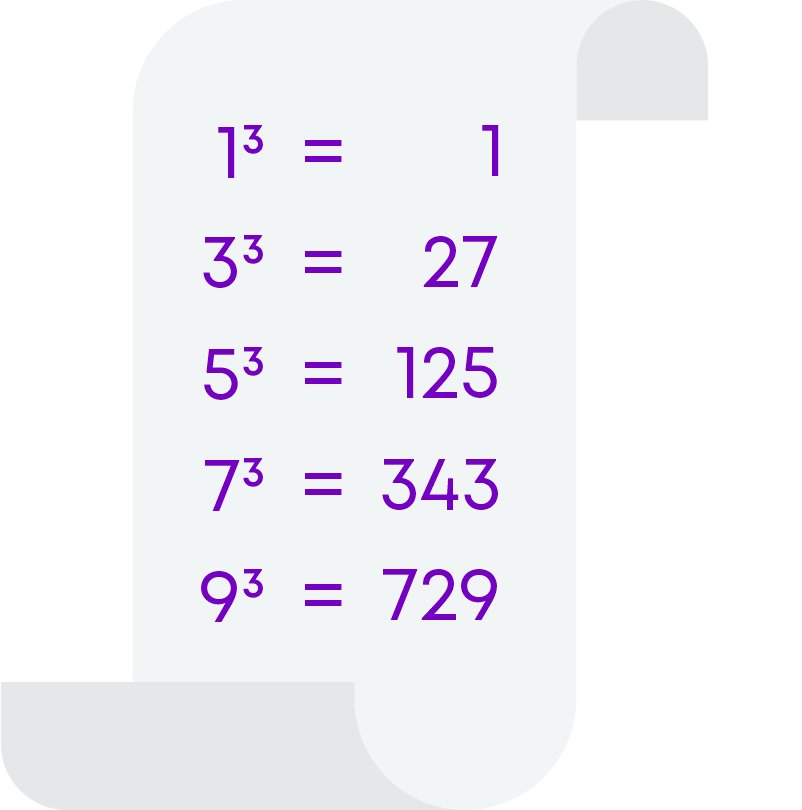
Observe the cubes of the odd numbers. Is there any pattern? The cubes of odd numbers are odd. For example, 1³ = 1, 5³ = 125.

Let us take the even numbers 2, 4, 6, 8 and 10 and their cubes.

Observe the cubes of even numbers. Is there any pattern? The cubes of odd numbers are even. For example, 2³ = 8, 4³ = 64.

Now, let us place the cube of the numbers 1 to 20 in a table.

Look at the numbers and their cubes. By observing the table, we can see that some numbers and their cubes have the same digit in the one’s place. Which of the numbers and their cubes have the same digit in the one’s place?

Cubes of the numbers ending in digits 0, 1, 4, 5, 6 and 9 are the numbers ending in the same digit.

Let us observe the numbers whose cubes end with the digits 2, 3, 7 and 8.

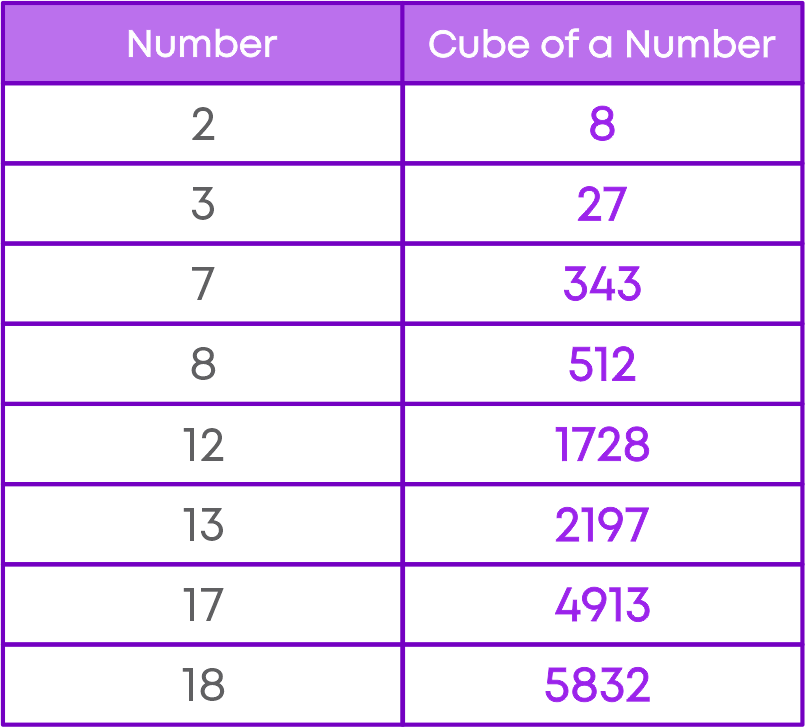
Look at the numbers and their cubes. A number whose one’s digit is 2 has a cube whose one’s digit is 8 and vice-versa. For example, 23 = 8, 83 = 512.

A number whose one’s digit is 3 has a cube whose one’s digit is 7 and vice-versa. For example, 3³ = 27, 7³ = 343.

Patterns in Cube Numbers

Did you know that cube numbers can be expressed as the sum of consecutive odd numbers? We have:

2³ = 3 + 5 = 8

2³ can be written as the sum of 2 consecutive odd numbers.

3³ = 7 + 9 + 11 = 27

3³ can be written as the sum of 3 consecutive odd numbers.

4³ = 13 + 15 + 17 + 19 = 64

4³ can be written as the sum of 4 consecutive odd numbers.

So, ‘n’ consecutive odd numbers are needed to obtain the sum as n³.

Now, let us explore the prime factorisation of cube numbers. Consider 8 and its cube 512.

8 = 2 × 2 × 2

8³ = 2³ × 2³ × 2³

Each prime factor of 8 appears three times in the prime factorisation of 8³.

So, each prime factor of a number appears three times in the prime factorisation of its cube, i.e.,

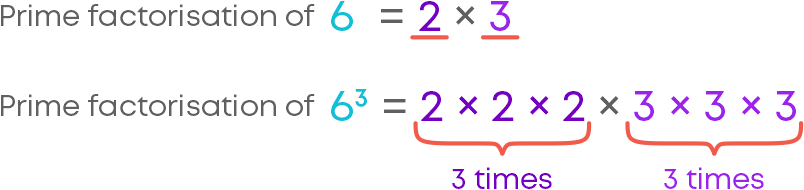
In the prime factorisation of a number, if each factor appears three times, then, is the number a perfect cube? For example, let us take the number 64. By prime factorisation,

64 = 2 × 2 × 2 × 2 × 2 × 2

Here we can see that prime factor 2 can be grouped in triples, i.e., 64 = 2 × 2 × 2 × 2 × 2 × 2

= 2³ × 2³

= (2 × 2)³

= 4³

Hence, 64 is a perfect cube.

We can identify if the given number is a perfect cube or not by looking at its prime factorisation. A number is a perfect cube only if its prime factorisation has prime numbers that occur three times.

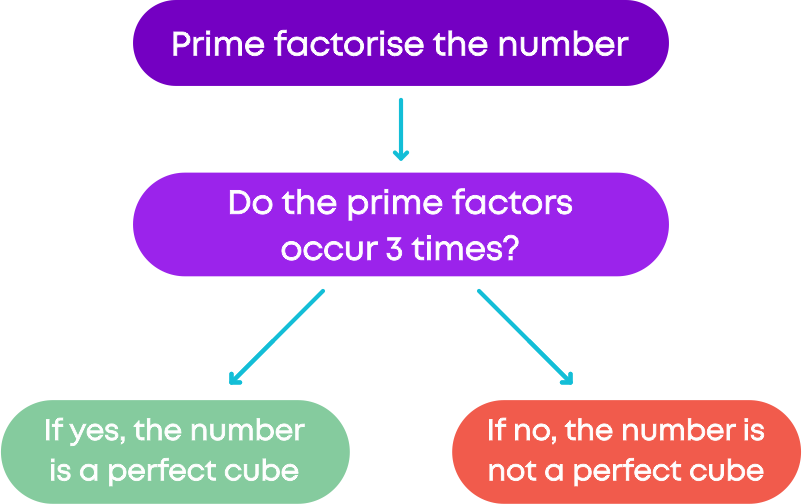
There are 2 types of questions where you will use the method of prime factorisation to make the given number as a perfect cube.

Type 1

To find the smallest number to be multiplied by the given number to get a perfect cube.

The strategy is to:

• Prime factorise the given number.
• Identify the prime factors that do not occur 3 times
• Find the product of such prime factors to get the smallest number.
• Multiply the smallest number to the given number, the obtained number will be a perfect cube.

Type 2

To find the smallest number by which the given number is to be divided to get a perfect cube.

The strategy is to:

• Prime factorise the given number.
• Identify the prime factors that do not occur 3 times
• Find the product of such prime factors to get the smallest number.
• Divide the given number by the smallest number, the obtained number will be a perfect cube.

The Cube Root of a Number

Consider this scenario:

Sana knows that the volume of a cube is 64 cubic cm. She wants to know what the dimensions of the cube are. How will she find it?

So, Sana must find the number which when multiplied by itself three times gives 64. But what is that number? Here, the cube of the number is known, and Sana needs to find the number which when multiplied by itself three times gives that cube number. In other words, Sana should find the cube root of the given number.

The cube root of a number is a value that, when multiplied by itself three times, gives the number. You know that 27 = 3 × 3 × 3 = 3³. Hence, the cube root of 27 is 3. This can be denoted as ∛27 = 3.

Finding the cube root is the inverse operation of finding the cube. Remember:

• If the cube is a 1 digit, 2 digit or 3 digit number, its cube root will be a 1 digit number.
• If the cube is a 4 digit, 5 digit or 6 digit number, its cube root will be a 2 digit number.

When the given number is a perfect cube, we find its cube root using the following steps:

• Find the prime factorisation of the number.
• Make groups of three similar prime factors.
• Choose one factor from each group and find their product.
• The product gives the cube root of the given number.

When we know that the given number is a cube number then estimation can be used. For example, let us see how to estimate the cube root of 195112.

Step 1: Form groups of three starting from the rightmost digit of 195112.

We get 195 and 112 as two groups of three digits each.

Step 2: Take the first group, i.e., 112.

The digit 2 is at its one’s place. We know that 8 comes at the unit’s place of a number only when it’s cube root ends in 2. Hence, we take the one’s place of the required cube root as 8.

Step 3: Take the second group, i.e., 195.

We know that 5³ = 125 and 6³ = 216.

195 lies between 125 and 216. Among 5 and 6, 5 is the smallest. We take the one’s place, of the smaller number as the ten’s place of the required cube root. Here one’s place of 5 is 5 itself. So, we take 5 as the ten’s place of the required cube root. Hence, we get ∛195112 = 58.