Introduction
If you look carefully, there are numbers all around us. Chances are you are reading this on a mobile or tab screen, both of which will have numbers written on them, either in the form of time, battery, date, etc. Look at objects in your room too, you will most likely find numbers representing some quantity or the other. Hence, it is very important to know your numbers.
Often, we come across large numbers in our day-to-day lives. Why do we need large numbers? To easily quantify huge amounts. For example, people have about 100000 hairs growing on their heads. There are 525600 minutes in a year. There are about 8000000 words in the English language.
Watch this video to know more about large numbers:
Concepts
The chapter ‘Knowing Our Numbers’ covers the following concepts:
To navigate to a particular concept, click on it.
Numbers Upto 1 Lakh
In Math, every digit in a number has a place value. Place value can be defined as the value represented by a digit based on its position in the number. We use place value tables to identify the place value of each digit of a number and to write the number name of a given numeral.
Learning how to find the greatest and smallest number is helpful in many ways. For example, Riya’s mother gave her some money to buy vegetables at the lowest cost. Riya visits three different shops. At each shop, a kilogram of potatoes costs ₹30, ₹27, and ₹38, respectively. So, using her knowledge of greatest and smallest numbers, Riya compares the prices and buys potatoes at the second shop where it costs the least amount, i.e., ₹27. She also realises that the third shop sells potatoes at the highest cost, i.e., ₹38.

When it comes to larger numbers, to compare two numbers, look at the number of digits. If the number of digits is different, the number with the greatest number of digits is greatest. If number of digits are same, the number with the greatest digit at the highest place is greatest. For numbers with same digit at the highest place, compare numbers using the digit at the next place.
The symbols of comparison are > (greater than), < (less than) and = (equal to).
For example:
- ✓ 1,00,000 > 98,765
- ✓ 98,765 < 1,00,000
- ✓ 99,999 = 99,999
Larger Numbers
Before the invention of numbers, counting was done using physical objects such as pebbles and sticks. After numbers came into existence, the need for adapting a standard system of counting arose. These systems were the Indian system and the International system of numeration.
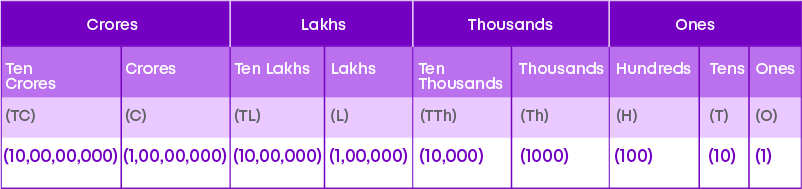
Values of the places in the Indian system of numeration are Ones, Tens, Hundreds, Thousands, Ten Thousands, Lakhs, Ten Lakhs, Crores and so on. Using this we can write number name for numerals and the expanded form of a number based on the Indian System of numeration. The following place value chart can be used to identify the digit in any place in the Indian system:
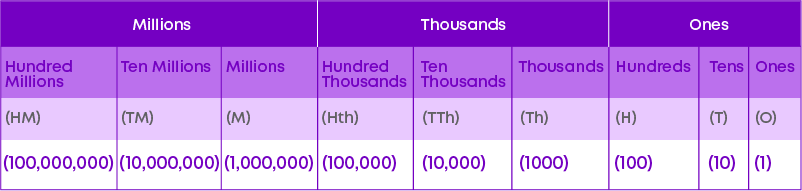
Values of the places in the International system of numeration are Ones, Tens, Hundreds, Thousands, Ten Thousands, Hundred Thousands, Millions, Ten Millions, Hundred Millions, Billions and so on. Using this we can write number name for numerals and the expanded form of a number based on the International System of numeration. Observe the International Place Value Chart carefully:
The use of commas helps in reading and writing large numbers. We can compare numbers represented in the Indian and International system by the placement of the commas.
- In the Indian system of numeration, we have commas after 3 digits starting from the right and thereafter every 2 digits. The commas after 3, 5 and 7 digits separate thousand, lakh and crore respectively. For example, the number 47000000 is written as 4,70,00,000.
- In the International system of numeration commas are placed after every 3 digits starting from the right. The commas after 3 and 6 digits separate thousand and million respectively. Taking the same example, the number 47000000 is written as 47,000,000.
Large Numbers In Practice
To understand operations on large numbers, we must first familiarise ourselves with the use of large numbers in the metric system. There are some standard units to represent length, weight, and capacity.
Length: Follow the rules below

Weight: Follow the rules below

Capacity: Follow the rules below

Once we are familiar with the metric system, we move on to learning how addition, subtraction, multiplication, and division works on large numbers:
- To add two or more large numbers, place the numbers in the place value table. Add the digits in the respective column by carrying over to higher place, if required.
- To subtract two large numbers, place the numbers in the place value table. Place the minuend (larger number) above and the subtrahend (smaller number) below in the place value table. Subtract the digits in the corresponding column by borrowing from higher place, if required.
- To multiply two large numbers, multiply the ones digit of the multiplier by the multiplicand, Place a 0 in the ones place and multiply the digit in the tens place of the multiplier by the multiplicand. Where multiplier is of 3 digits, place a 0 in the ones place and tens place. Multiply the digit in the hundreds place of the multiplier by the multiplicand. Add the products
- To divide two large numbers, take the first digits of the dividend, the same number of digits that the divisor has. Multiply the digit of the quotient by the divisor, write the result beneath the dividend and subtract it. After subtraction, bring down the next digit of the dividend and repeat previous steps until there are no more remaining numbers in the dividend.
Estimation
Do you think estimation is useful in our daily life? Yes! Just ask anyone in your family who reads or watches news channels. News articles use estimation to report large numbers where it is not possible to give an exact count.
Observe the news headline below:

Here, it is not possible to know the exact number of cases, so an approximate figure (500,000+) has been given for the readers to get an idea of the number of cases.Let us discuss the estimation of numbers to the nearest tens, hundreds, and thousands by rounding off.
- To round off a number to the nearest tens, look at the ones digit. If the digit at ones place is 1, 2, 3 or 4, replace ones digit by 0. If the digit at ones place is 5, 6, 7, 8 or 9, replace ones digit by 0 and add 1 to the digit at tens place.
- Similarly, to round off a number to the nearest hundreds, look at the tens digit. If the digit at tens place is 1, 2, 3 or 4, replace tens and ones digit by 0. If the digit at tens place is 5, 6, 7, 8 or 9, replace tens and ones digit by 0 and add 1 to the hundreds place.
- To round off a number to the nearest thousands, look at the hundreds digit. If it is less than 5, then round the number down by changing the digit at hundreds, tens and ones place to zero. The digit at the thousands place remains unchanged. If it is 5 or more, then round off the number up by adding one to the digit at thousands place. Change the digit at hundreds, tens and ones place to zero.
There are many situations where we must estimate the outcome of operations like sum, difference, or product; this is done by rounding off the addends, subtrahend and minuend, and multiplicand and multiplier, respectively, to get a quick, rough answer. Then, use mental math to multiply the resultant numbers found in the previous step.
Brackets
Use of brackets allows us to avoid confusion in the problems where we need to carry out more than one number operation. So, with the use of brackets, we can simplify the expression and avoid the confusion in the way we calculate
For example, you want to make a flowerpot with the help of sticks. So, you buy 106 sticks and the cost of each stick is ₹6. You calculated the total amount of these sticks as 6 × 106. As the calculation is difficult, you used brackets to write 106 as (100+ 6), so that the calculation becomes
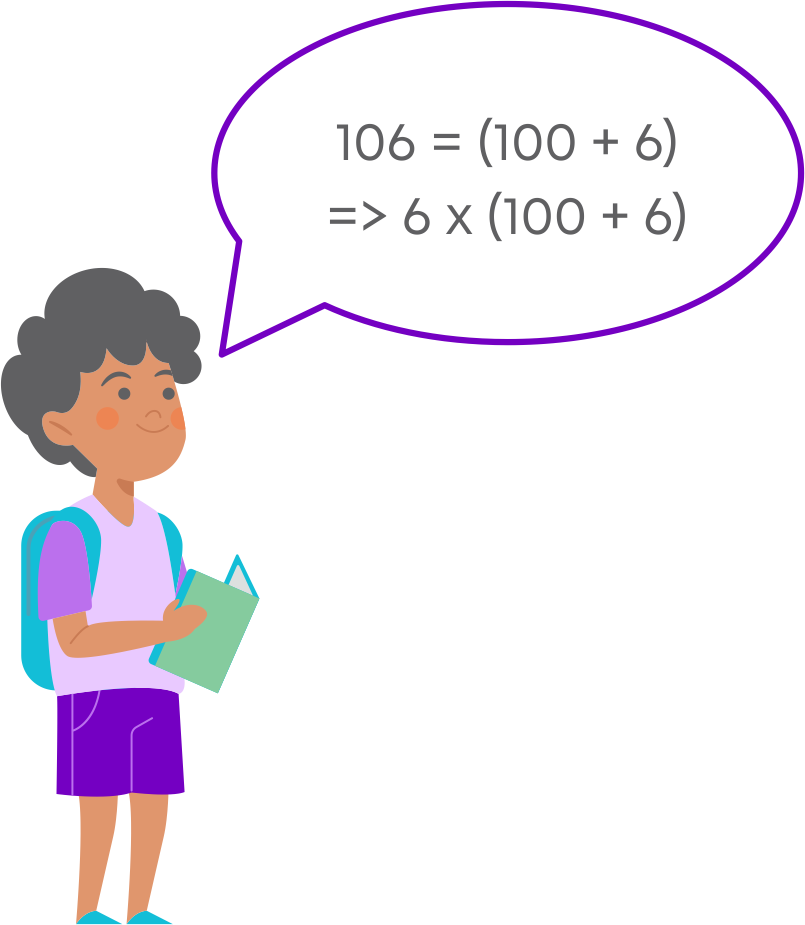
To solve this expression, we must expand the brackets first, then we apply the operations on them. To expand a bracket means to multiply each term in the bracket by the term outside the bracket. Here, the numbers inside the brackets 100 and 6 will be multiplied by the number outside as follows:
- 6 × (100 + 6)
- = 6 × 100 + 6 × 6
- = 600 + 36
- = 636
Hence, we see that the use of brackets makes the calculation simpler.
Roman Numerals
When giving an exam, do you remember how you write which class you are in? Right from class 1, we are taught to write our class in Roman numeral form.
One of the early systems of writing numerals is the system of Roman numerals. Any number is represented using these basic symbols:
I V X L C D M
Each numeral has its own value as shown:

There is no Roman numeral for zero.
Some other examples where you will find Roman numerals are in books for chapter numbers, in fancy clocks or watches, or even for mobile phone model numbers (e.g., iPhone X means the iPhone 10).

To write a number in the Roman numeral system, we must follow certain rules:
- Rule 1: Repetition of a symbol in Roman numerals means addition. The symbol should be added as many times as it is repeated.
- Rule 2: If a symbol of smaller value is written to the right of a symbol of greater value, its value gets added to the value of the greater symbol.
- Rule 3: If a symbol of smaller value is written to the left of a symbol of greater value, its value is subtracted from the greater symbol.
- Rule 4: When a smaller numeral is placed between two larger numerals, we first subtract it from the larger numeral immediately following it and then we follow other rules for writing Roman numerals.
- Rule 5: The symbols V, L, D are never written to the left of the symbol of greater value.
Common Errors
The following are the topics in which students make common mistakes when dealing with large numbers
- 1. Place Value
- 2. Comparing Numbers
- 3. Rounding Off
- 4. Adding Numbers
- 5. Subtracting Numbers
- 6. Multiplying Numbers
- 7. Dividing Numbers
Place Value
How do we write the number five thousand and nine?
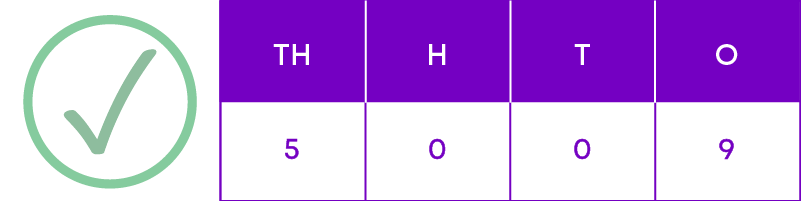
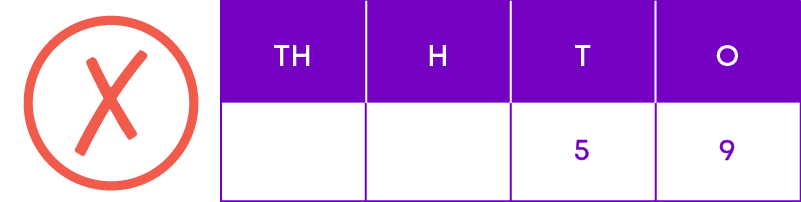
Remember: If we have no ones, tens, hundreds etc. then we must write 0 in the appropriate column.
Comparing Numbers
Which is greater, 78 or 102?

We always order the numbers based on their place value, not on value of the digit.
Rounding Off
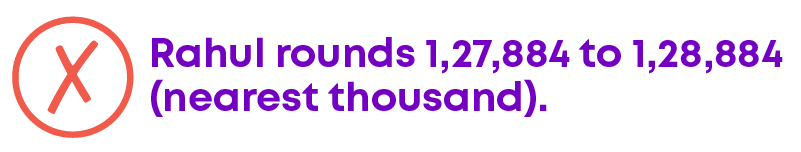
Rahul misapplies the rule for “rounding up” and changes the digit in the designated place while leaving digits in smaller places as they are.
We round the number 1,27,884 to 1,28,000 to the nearest thousand. That is places to the right of thousand becomes zero.
Adding Numbers
Understanding the place value of the digits in the calculation:
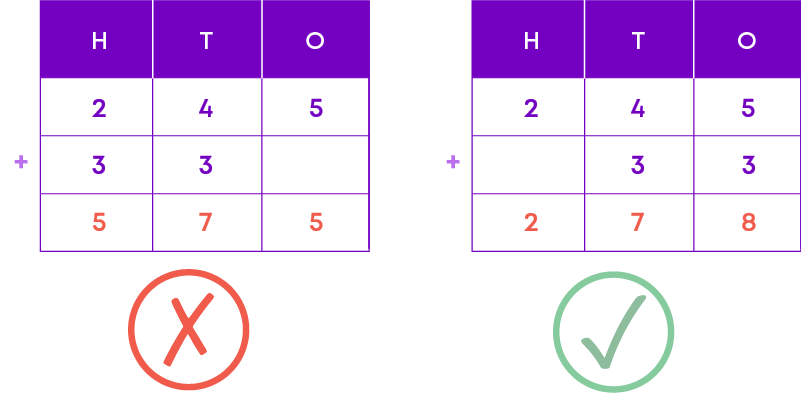
Remember: While putting the numbers in the place value chart, always start from extreme right column. In this case its ones.
Subtracting Numbers
Subtracting the smaller digit in a column from the larger digit, regardless of which appears in the top:
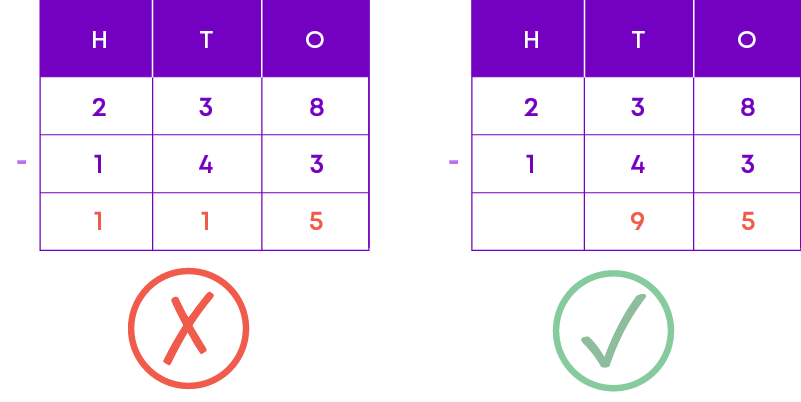
Remember: In subtraction, the order cannot be changed. We always subtract the bottom digit from top digit.
Multiplying Numbers
Multiplying multidigit numbers by ignoring place value.
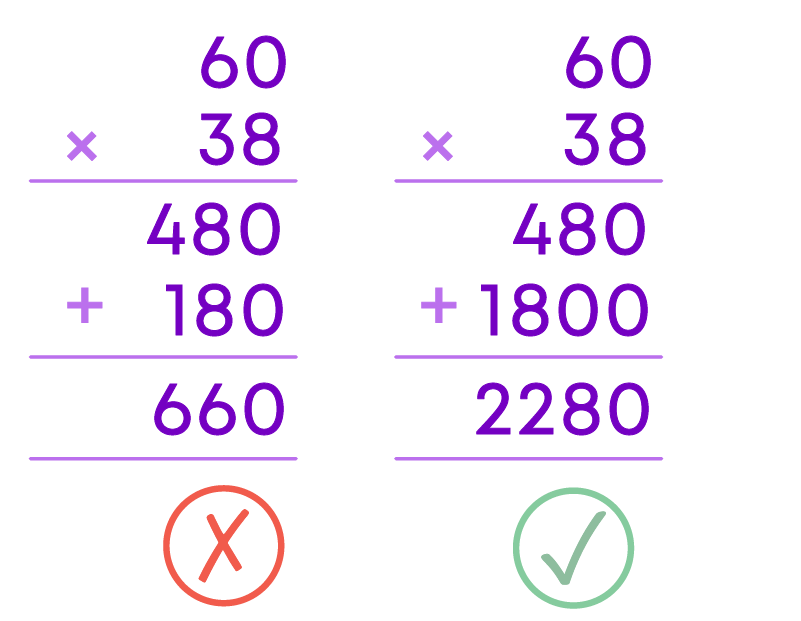
In the first image, multiplication is done right, but it has been ignored that the 3 in the tens place means 30.
Thus, 30 × 60 = 1,800.
Dividing Numbers
Dividing four-digit numbers using long division, and the quotient may have a zero.

Remember: After the first subtraction we bring down 2 but 4 does not go into 2, so place a zero in the quotient and then bring down another digit 0.
Conclusion
We have covered all the sub-concepts in this chapter. Remember, while solving word problems using large numbers, analyse the problem carefully to identify what is given and what we must find. Then, interpret the keywords given in the question. Find a suitable strategy to solve the given problem by identifying the right mathematical operation, then perform calculation and find the result.
Now that you are familiar with large numbers, can you solve this riddle?
I am larger than 4 hundred thousand. I am less than half a million. I am odd. My hundreds digit is my smallest digit. Who am I among the following options?
1) 475,346
2) 542,109
3) 413,077
4) 409,101




















































