Introduction
A commonly used method for comparing two quantities of the same type is by taking the difference between the quantities. In many situations, a more meaningful comparison between quantities is made by division. For example, if we wish to compare the lengths of an ant and a grasshopper, taking the difference does not express the comparison. The grasshopper’s length, typically 4 cm to 5 cm, is too long when compared to the ant’s length, which is a few mm. The comparison will be better if we try to find how many ants can be placed one behind the other to match the length of the grasshopper. So, we can say that 20 to 30 ants have the same length as a grasshopper.
Thus, if we want to know how much more or less one quantity is from the other, then we compare them by taking their difference. But if we want to know how many times one quantity is that of the other, we compare the two quantities by division.
This comparison of two quantities by division is called ratio.
Watch the video to know more:
Concepts
The chapter ‘Symmetry’ covers the following concepts:
Ratio
The ratio of the two quantities of the same kind and in the same units is a fraction that shows how many times one quantity is of the other. Ratio is denoted by using the symbol ‘:’. The ratio of two quantities a and b (b ≠ 0) is a/b and is denoted by a : b.
a : b is read as a is to b.
Remember: A ratio can be computed only when two quantities are in the same units.
Two quantities may not always be in the same units. In that case, we need to convert them into the same units. Finally, we need to reduce them to their lowest terms. This form of ratio is called the simplest form of the ratio. Ratios have no unit.
The concept of ratio and proportion has real-life applications in many ways. For example, a shopkeeper sells 2 bars of chocolate at ₹10. You want to give few pieces to your friends, so you decide to buy 6 bars. How do you calculate the cost to buy 6 bars of chocolate? You can do so using ratio and proportion:
2 bars ---> 10 rupees
6 bars ----> x

We come across situations when we are required to share or distribute a certain quantity in the given ratio. For example, sharing of profits in a business. In such cases, we need to convert the ratio into fractional parts and then multiply the given quantity with each of the fractions so obtained. This gives us the required share.
Equivalent Ratios
Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number.

There could be many equivalent ratios of the same ratio. In the case of equivalent ratios, only their value changes but they represent the same portion of the quantity.
Did you know? We can find the value of the missing term in a ratio given its equivalent ratio.
The ratio may have a missing numerator or missing denominator. Once that number is found we can use it to find the value of the unknown.
Anmol and Pratik are solving one such puzzle.
12/20 = x/5 = 9/y
Anmol tries to divide the denominator of the first fraction by 4 and he gets 5, which is the denominator of the second fraction. Dividing the numerator and denominator by 4, he gets,
12/20 = 3/5
Hence, the value of x is 3.
Now, it is Pratik’s turn to find the value of y.
12/20 = 3/5 = 9/y
He tries to multiply the numerator of the second fraction by 3 and gets 9, which is the numerator of the third fraction. Multiplying the numerator and denominator by 3, he gets,
3/5 = 9/15
Hence, the value of y is 15.
Therefore, 12/20 = 3/5 = 9/15
Proportion
If two ratios are equal, we say that they are in proportion and use the symbol ‘::’ or ‘=’ to equate the two ratios. Four numbers are said to be in proportion if the ratio of the first two is equal to the ratio of the last two, i.e., a, b, c, and d are in proportion, if a/b = c/d.
If two ratios are not equal, then we say that they are not in proportion. In a statement of proportion, the four quantities involved when taken in order are known as respective terms. First and fourth terms are known as extreme terms. Second and third terms are known as middle terms.

When finding the unknown term in a proportional relationship, first write the ratios with an equal symbol in between so that we understand that they are equivalent to each other. Then, find a number which when multiplied or divided from the numerator and denominator of the first ratio gives the unknown value of the second ratio.
Anmol and Pratik are busy solving yet another puzzle. This time, it seems to be related to an unknown value when all four terms are in proportion.
If 15, 45, x and 120 are in proportion, then find the value of x.
Anmol knows that since it is given that all the four terms form a proportion, then their ratios must be equal!
Ratio of 15 : 45 = 15/45 = 1/3 = 1 : 3
Ratio of x : 120 = x/120
So, according to the given information, 1/3=x/120
You know that 3 multiplied by 40 gives 120, hence, multiplying the numerator and denominator of 1/3 by 40, we get:
1/3=40/120
Therefore, the value of x is 40.
Ratio and proportion are also commonly used while representing data in a concise manner. Some common examples are demographics and maps. Have you ever looked at a map or had to draw a map? You will notice that it is impossible to draw the actual distance between places on a piece of paper, which is why we use a scale so that the drawn distance can be shown as a proportion to the original distance.
For example, on a road map, the distance between Dallas and Houston is 7 inches. What is the actual distance between the cities if the map scale is 1 inch = 50 kilometres?
Let ‘d’ be the actual distance between the cities.
1/50=7/d [Write a proportion]
1 × d = 7 × 50 [Find the cross products]
d = 350 [Multiply]
Hence, the distance between the cities is 350 kilometres.
Unitary Method
The method in which first we find the value of one unit and then the value of required number of units is known as unitary method.
Value of one article = Value of the given number of articles / Number of articles
Value of required number of articles = value of one article × required number of articles
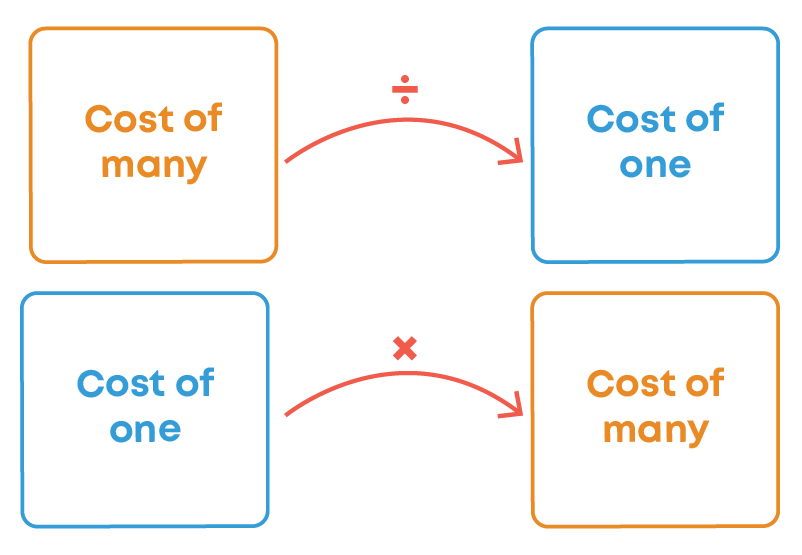
The unitary method helps us understand the unit price when a thing is measured in dozens, kg, etc.
Common Errors
The following are the topics in which students make common mistakes when dealing with ratio and proportion:
- 1. Representation of ratio
- 2. Simplification of a ratio
- 3. Comparing ratios of same unit
- 4. Order in the ratio is important
- 5. Unitary method
Representation Of Ratio
In how many ways can you represent a ratio? One, two, or three? Look at this example.

All three are the representations of a ratio. We should be able to use all three forms of a ratio interchangeably and with ease.
Simplification Of A Ratio
Ratios can also be simplified. A common error is that if a ratio is not written in fraction form, we forget to simplify it.

We see that 6 : 8 is a ratio but is not in simplest form. However, because the form of the ratio is not fraction form, we make an error by often leaving it alone.
Comparing Ratios Of Same Unit
The length of a pencil is 15 cm, and its diameter is 9 mm. What is the ratio of the length of the pencil to its diameter?
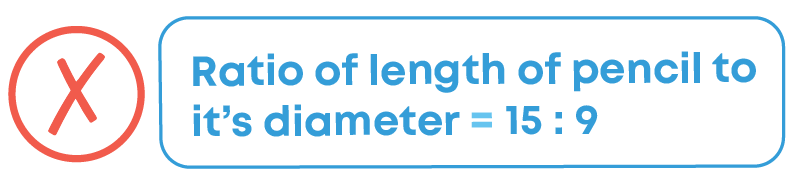
Since the length and the diameter of the pencil are given in different units, we first need to convert them into the same unit. Thus, length of the pencil = 15 cm = 15 × 10 mm = 150 mm.
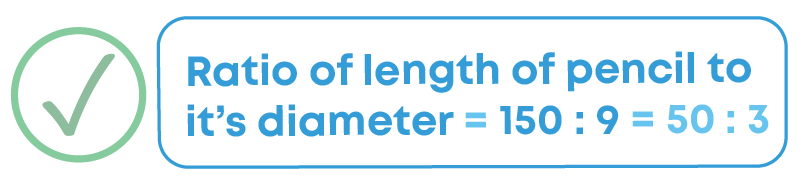
Order In The Ratio Is Important
Did you know that order in the ratio is important?

Ratio 3 : 2 is different from 2 : 3. Thus, the order in which quantities are taken to express their ratio is important.
Unitary Method
You go to the shop to purchase envelopes. The shopkeeper says, ‘Cost of 105 envelopes is ₹350’. But you have only ₹100. How many envelopes can you buy with ₹100? Let us use the ‘unitary method’.
The unitary method is a method where we find the value of a single unit from the value of multiple units and the value of multiple units from the value of a single unit.
Observe the two responses below:
Response 1:

Response 2:

Using the unitary method,
- First, find the number of envelopes that can be bought in ₹1. To do that, divide the total number of envelopes by 350.
- To find the number of envelopes that can be purchased in ₹100, multiply the cost of 1 envelope by 100.
Conclusion
Now that you know everything about ratio, proportion, and the unitary method, can you solve this puzzle?
The table below shows the weights of apples sold of each variety. What is the ratio of the weights of Kiku apples to the weights of Ambrosia?




















































