Linear Equations with Linear Expressions on One Side and Numbers on the Other Side

This statement has an ‘equal to’ sign, with an expression on its left and a number on its right. Such a mathematical statement is called an equation.

• The expression on the left of the '=' is the left-hand side or the LHS of the equation.
• The expression on the right of the '=' is the right-hand side or the RHS of the equation.

What is the difference between the two equations given below?

A linear equation in one variable will be of the form ax + b = 0, where a and b are rational numbers and x is a variable, whose highest degree is 1. A linear equation can have variables either on the left side of the ‘=’ sign or on the right side. Examples: 3m – 1 = 5, 10 = 3n + 2, -5 = p + 9.

Consider the equation: 5m – 8 = 17

The variable in this equation is ‘m’. The highest power of ‘m’ is 1. Hence, this is a linear equation.

Consider another equation: 7m³ – 1 = 10

Here, ‘m’ is the only variable in the equation. But its power is ‘3’. Equations which have a variable whose power is more than 1 are not linear equations.

Let us practice solving equations by using each of these methods. How do we solve linear equations by the balance method?

To solve an equation by balance method:

• We need to keep the variable terms on one side and constants on the other side of the equation.
• Perform the same operation on both sides of the equation.
• Apply the balance method until we have the variable on one side and its value on the other side.

Example: Solve y + 9 = 2 using balancing method.

We must keep only the variable on the LHS of the equation. For this, we must eliminate the constant from the LHS. So, we subtract 9 from both the sides of the equation.

y + 9 - 9 = 2 – 9

y + 0 = -7

y = -7

How do we know that '-7' is the correct value of ‘y’?

For this, we substitute y = -7 in the LHS of the given equation and compare the value with RHS.

y + 9 = -7 + 9 = 2

LHS = RHS

So, we see that the value y = -7 makes the LHS equal to the RHS. Hence, -7 is the correct value of y in the given equation.

Let us learn how to solve a linear equation by the transpose method. To solve an equation by transpose method,

• We need to keep the variable terms on one side and constants on the other side of the equation.
• While transposing the terms, the operation of the terms changes to the opposite operation.
• Apply the transpose method until we have the variable on one side and its value on the other side.

Find the root of the equation 10 = 3x – 5.

Let us solve this equation by using the transposing method. Transpose 5 from the RHS to the LHS.

10 + 5 = 3x

15 = 3x

Transpose 3 to the LHS to keep only ‘x’ on one side.

15 3 = x

x = 5

∴ The root of the equation is 5.

To solve contextual problems which require linear equations in one variable, we follow a simple strategy.

Linear Equations with Variables on Both Sides

Can we have linear equations with variables on both sides? Observe the following equation.

Yes, linear equations can have variables on both sides. But the variable on both sides should be the same. Then, it will be a linear equation in one variable.

To solve a linear equation having variables on both sides, we follow these steps:

• Transpose the variable terms to one side and the constant terms to the other side of the equation.
• Simplify the terms on both sides.
• Solve the equation so obtained to find the value of the variable.

Rahul and Deepa solved a linear equation in different ways. The equation is

x + 1 5 = 7 10 + 4x

Rahul first transposed the variables and then the constant, whereas Deepa transposed the constants first and then the variables. But both arrived at the same solution for ‘x’.

What can we infer from this?

We can either transpose the variable first or the constants and then find the solution for the variable.

To solve a contextual problem which uses linear equations with variable on both sides, we follow the strategy given below.

Consider this example: Twice a number minus 16 is equal to the sum of the number and 5 Find the number.

First, let us form the equation according to the given statement. Let the number be ‘x’. Twice the number will be ‘2x’. So, the equation is

So, the equation is 2x – 16 = x + 5

Use the method of transposition so that the variables are on the LHS, and the constants are on the RHS.

2x – x = 5 + 16

x = 21

Hence, the number is 21.

Reducing Equations to Simpler Form

Consider the equation y - 4 2 = 2y + 1 6 . Following are steps to reduce the complex equation to simpler form:

Step 1: We use the cross-multiplication method to eliminate the denominators.

That is,

• We multiply the numerator on the LHS with the denominator on the RHS
• And multiply the numerator on the RHS with the denominator on the LHS

Step 2: Find the product of the terms on the LHS and the RHS.

This is a simple form of the given equation.

Here is an equation: a 2 = 2a - 1 3

The denominators on the two sides are 2 and 3. Let us equalise the denominator by converting each of the denominators to their LCM. LCM of 2 and 3 is 6. Now, make the denominators 6. On the LHS, we have

a x 3 2 × 3 = 3a 6

On the RHS, we have

(2a-1) × 2 3 × 2 = 2(2a-1) 6

So, we have

3a 6 = 2(2a-1) 6

Multiplying both sides by 6, we have

3a = 2(2a-1)

Now, let us see what happens when we cross-multiply:

a 2 = 2a - 1 3

We have,

3a = 2(2a – 1)

So, you see that cross-multiplication is the same as reducing the equation to a simple form by balancing method.

To reduce a complex linear equation to a simpler form, follow the below points:

• If the equation is of the form a b = c d

• If the equation is of the form a b ± m = c d ± n

Consider the equation:

The first step to solve this equation is to reduce it to a simpler form. For this, first transpose b3 to the LHS. We get,

Then, simply the LHS:

The LCM of the denominators = 6. Hence, we get

Now, cross-multiply the terms of the LHS and RHS:

Equations Reducible to the Linear Form

Consider the equation.

Let us move the terms with variables to the left-hand side of the equation.

Now, let us move the constant on the right-hand side to the left-hand side.

On simplifying the equation, we get

This is now a simpler form of the equation. Once we have transposed all the terms to the left-hand side, the value on the right-hand side is 0. This is the standard form of a linear equation in one variable.

Consider the equation:

Let us try to reduce the equation to a linear form. Use the method of cross- multiplication to eliminate the denominators.

• Multiply the numerator on the LHS with the denominator on the RHS.
• And multiply the numerator of the RHS with the denominator on the LHS.

The given equation is now reduced to linear form. Now, we solve the equation to find the value of the variable.

In general, the standard form of a linear equation in one variable can be represented as:

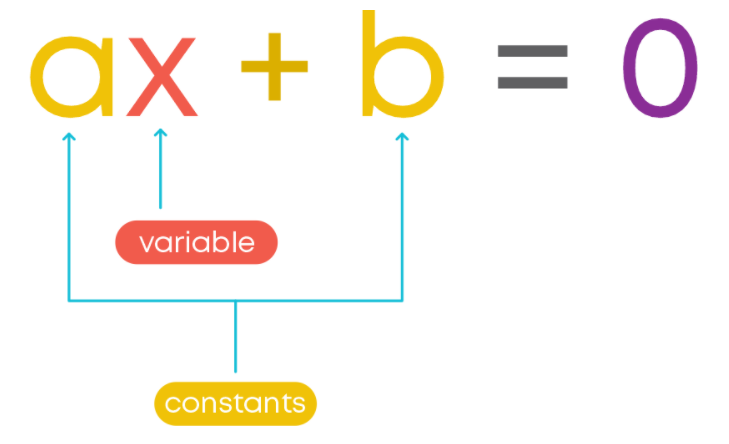
Let us see how to solve an equation which is not in linear form. Consider the example:

This equation is not in the linear form since the expression on its LHS is not linear. Can we convert this equation to linear form? Yes, we can convert this equation into linear form.

• Cross - multiply the terms on the LHS and the RHS.

Now, it is in the linear form. We can solve it by reducing to simpler form.