Introduction
We see many plane figures and solid shapes around us. Plane figures are of two-dimensions (2-D) and the solid shapes are of three-dimensions (3-D).
Let us watch this video to know more about the solid shapes.
From the video, we learn that
- Every 3-D shape can be represented as a flat 2-D shape.
- Different sections of a solid can be viewed in ways like slicing or cutting the solid and observing 2-D shadow of 3-D shape.
- Also, solid shapes when looked at from different positions will look differently.
You must have seen these objects around you:

Observe that these objects have length, breadth, and height.

So, they all occupy space and have three dimensions.
Hence, they are called three dimensional shapes or 3-D shapes or solid shapes.
Let us draw these shapes in our notebook:
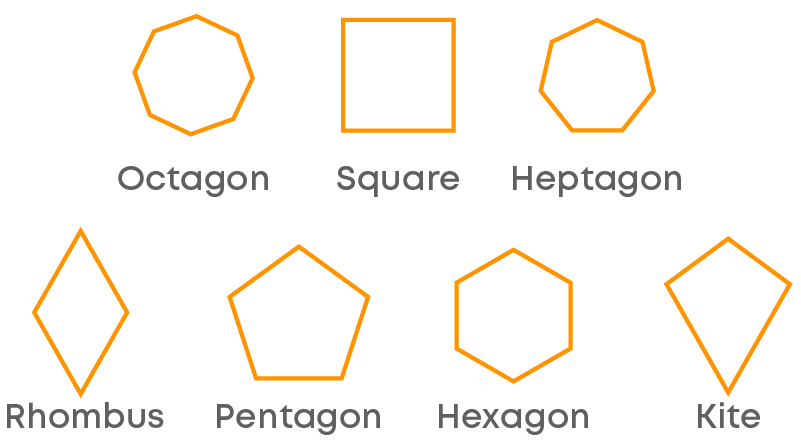
Observe that these objects have only length and breadth. So, they all have two dimensions.
Hence, they are called two dimensional shapes or 2-D shapes or plane figures.
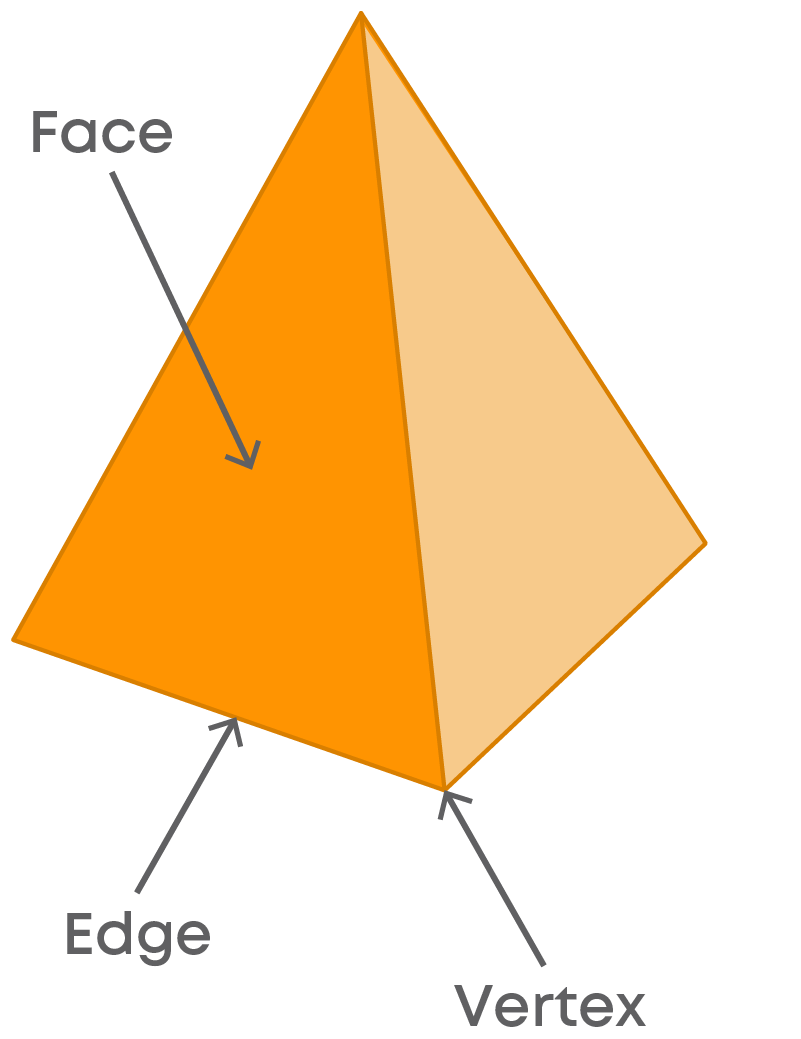
The figure below represents a square pyramid.

Observe that it has 5 corners. These corners are called its vertices.
Also, there are 5 flat surfaces for this shape. These flat surfaces are called its faces. The most important are the 8 line segments making the outline of the shape. These line segments are nothing but its edges.
Concepts
The chapter ‘visualising solid shapes’ covers the following concepts:
Relation Between 2D and 3D Shapes
A flat surface can be rolled to form a curved surface, and if you open a roll, you can get a flat surface. Consider a shape having a flat surface:

Let us roll it

Now this surface is a curved one. Again, by opening this roll, we get a flat surface.

Let us consider a 3-D solid shape shown below:

Can we have an outline of this shape in 2-D? Yes, we can draw an outline of 3-D solid shape in 2-D. Such an outline of 3-D solid shape in 2-D is the net of solid shape. This outline when folded results in a 3-D shape.
An outline of a 3D solid shape in 2D is called the net of the solid shape.
You must have seen this 3-D solid shape:

We can open this 3-D solid shape from its edges to get the net of that solid.

So, a net is a kind of an outline in 2-D. We can fold along this outline to get the 3-D shape.
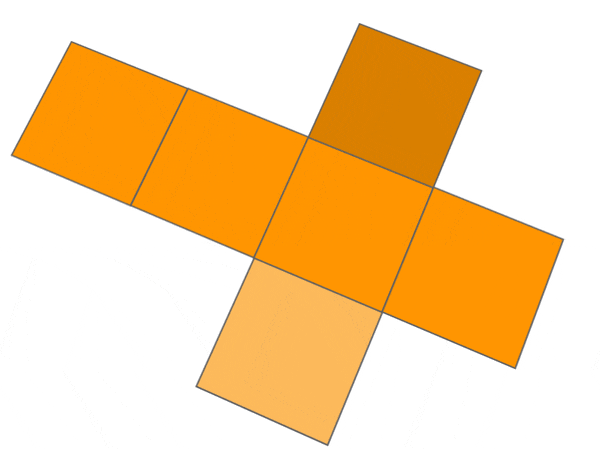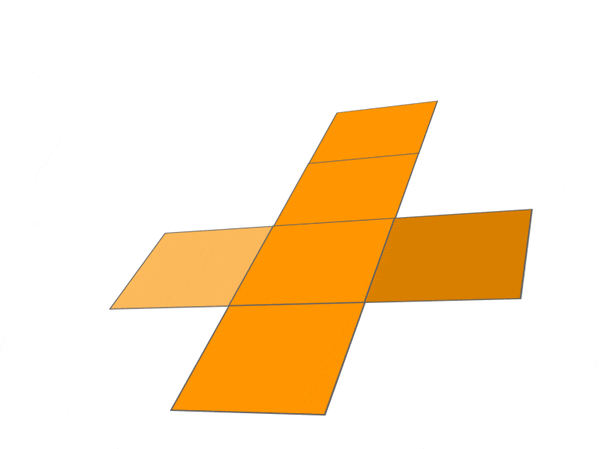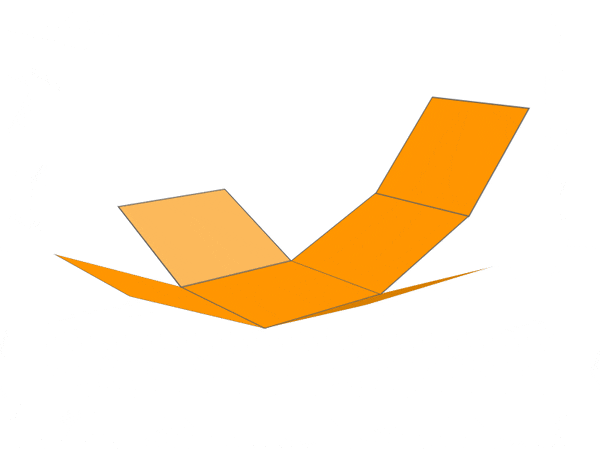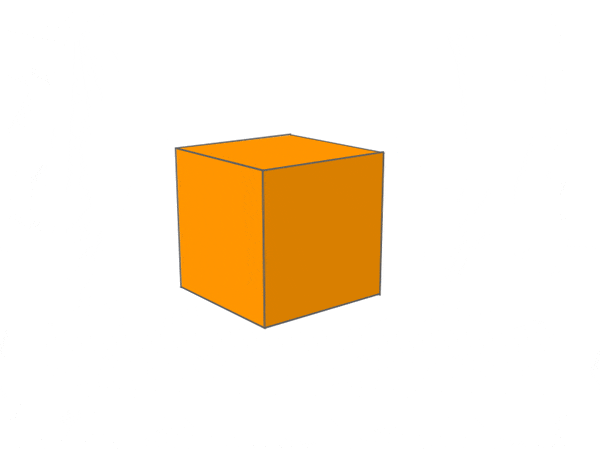
Hence, we can say that a net is a 2-D representation of 3-D solid shape.
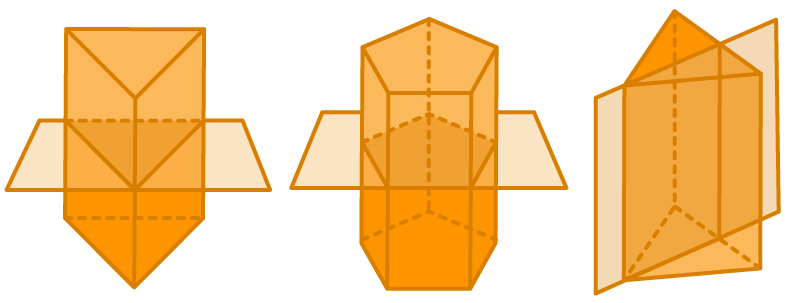
Let us see the nets of different solid shapes:
CONE

CUBE

CUBOID
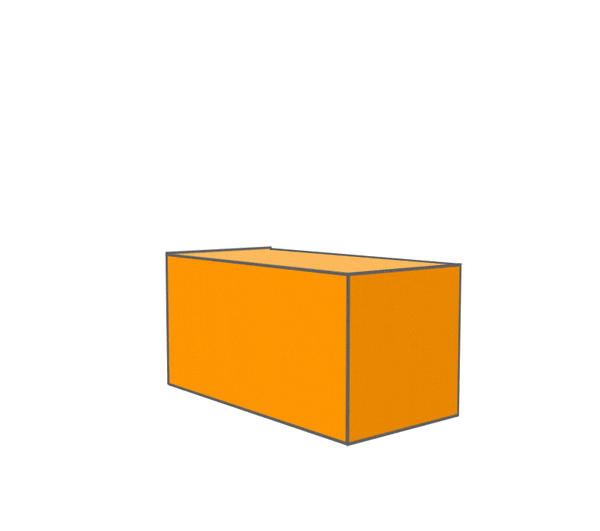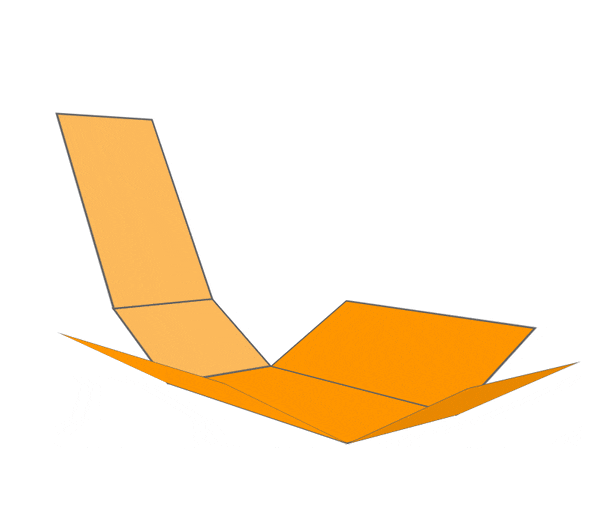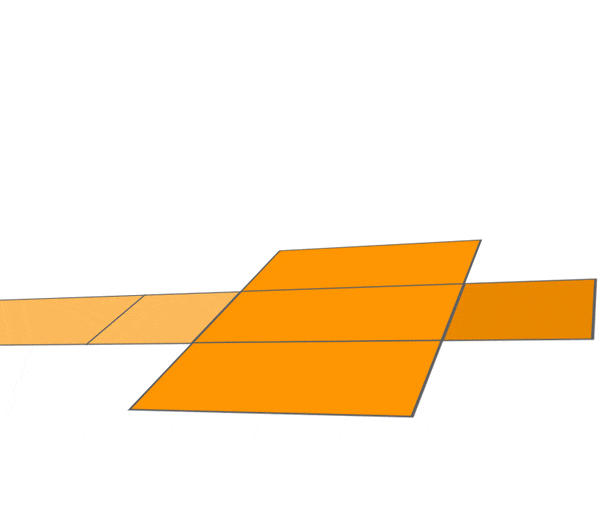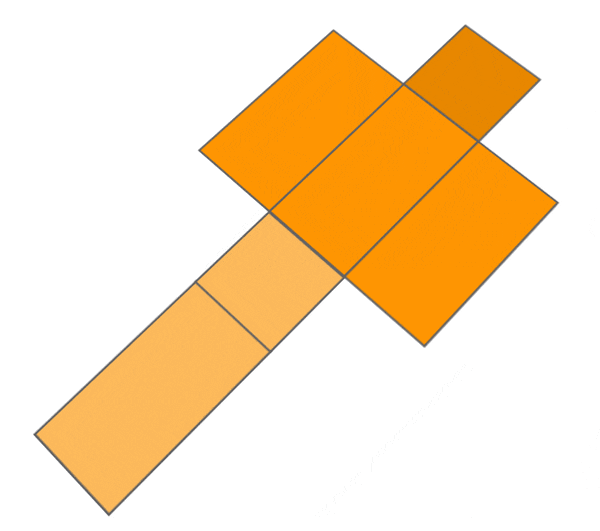
CYLINDER

TRIANGULAR PRISM
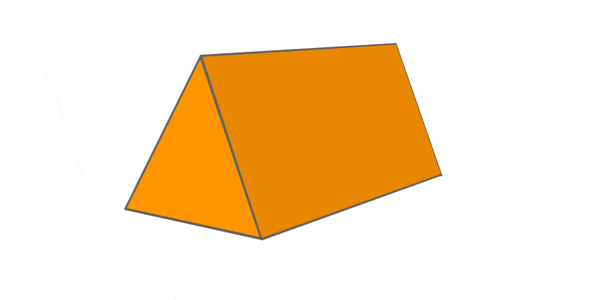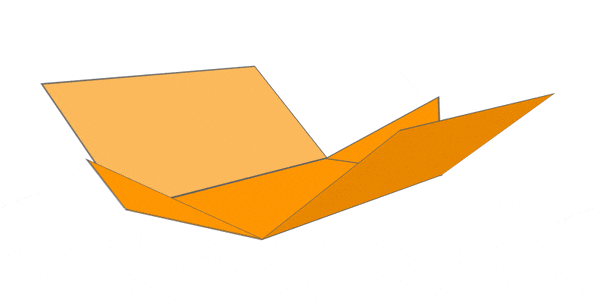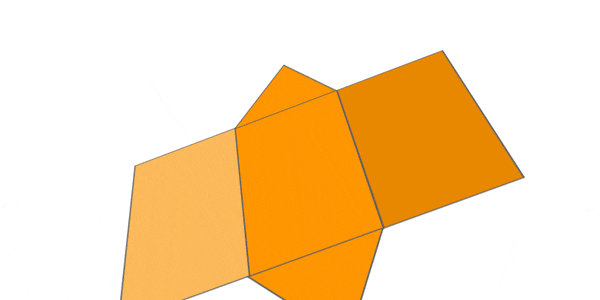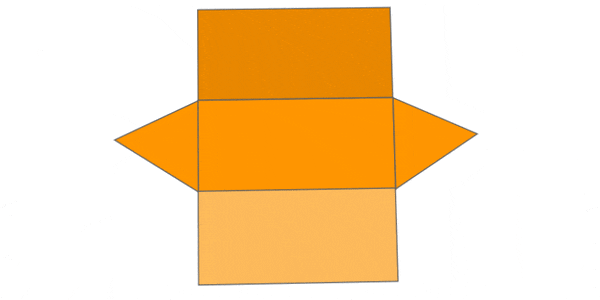
TRIANGULAR PYRAMID

PENTAGONAL PYRAMID

We can find the net of given solid with the help of its plane and curved surfaces.
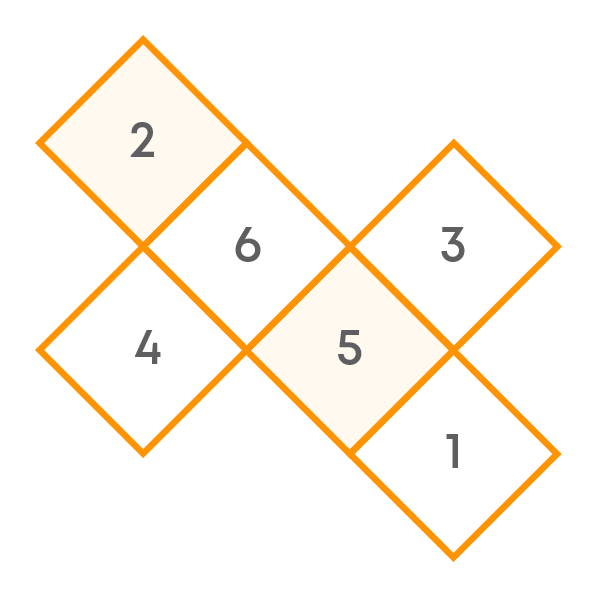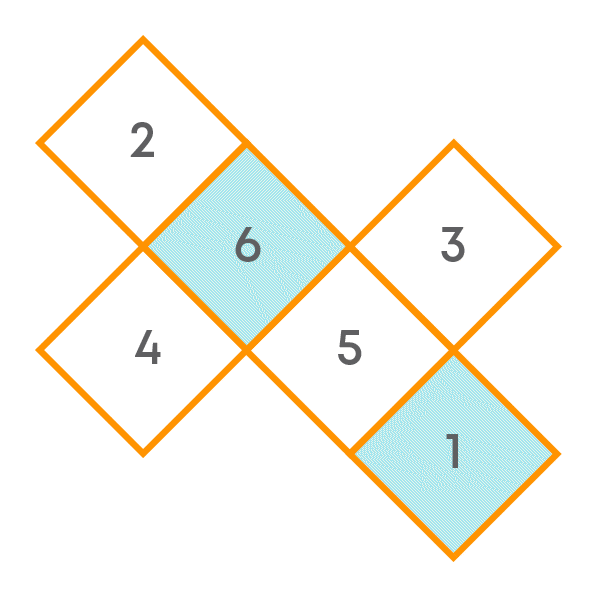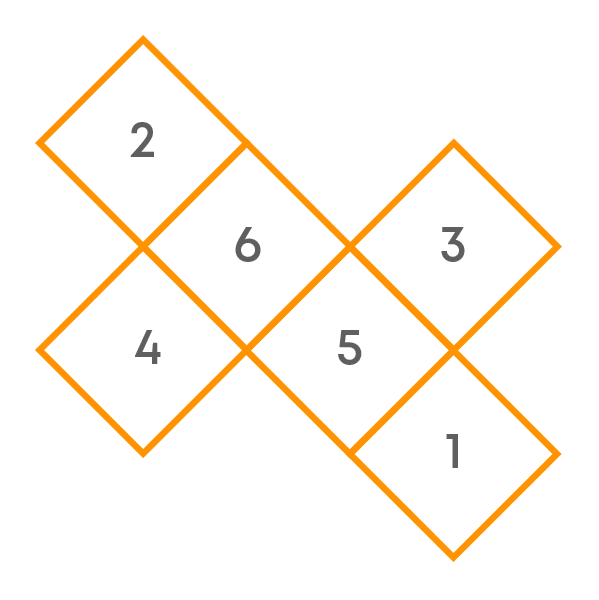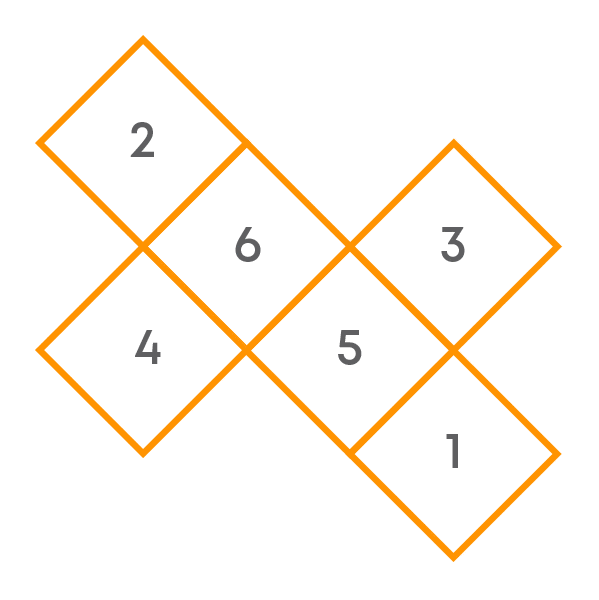
A dice is a cube with dots on each face. Opposite faces of a die always have a total of seven dots on them.

If we open a die from its edges, we get its net.

So, the net of a die is made up of 6 squares. If numbers in each square indicates the number of dots in that box, we get the figure as shown.
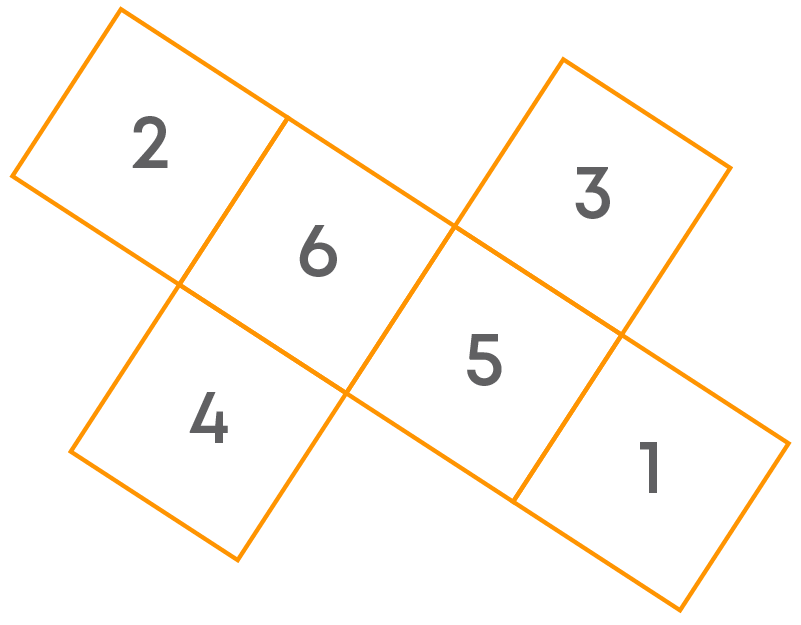
The numbers on opposite faces total to 7.
Consider the figure given below:

Observe that the sum of the two numbers on the opposite faces is not always 7.
Hence, this is not the net of a die.
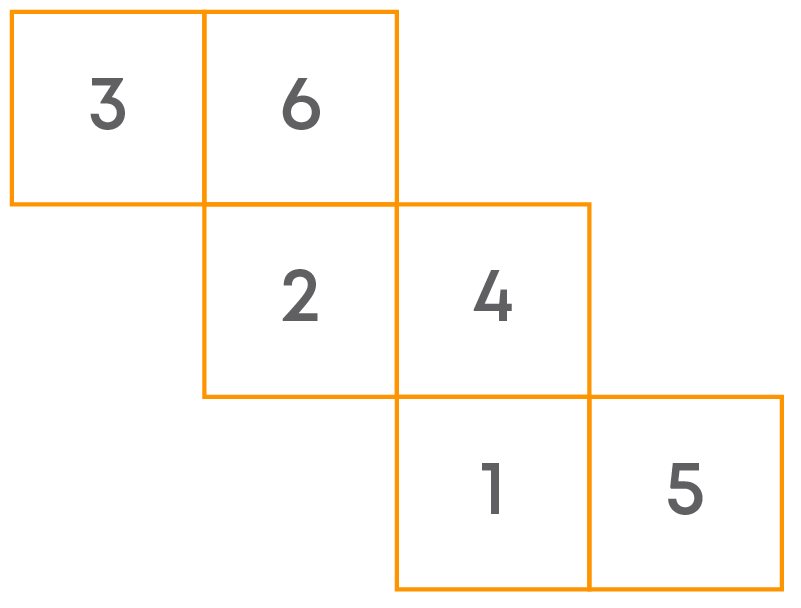
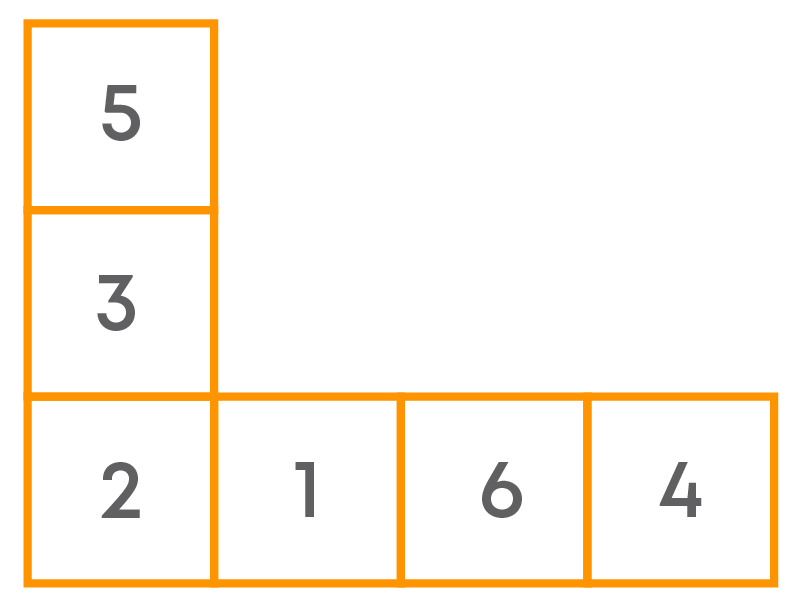
Here is the net to make a die. The numbers in each square indicate the number of dots in that square.
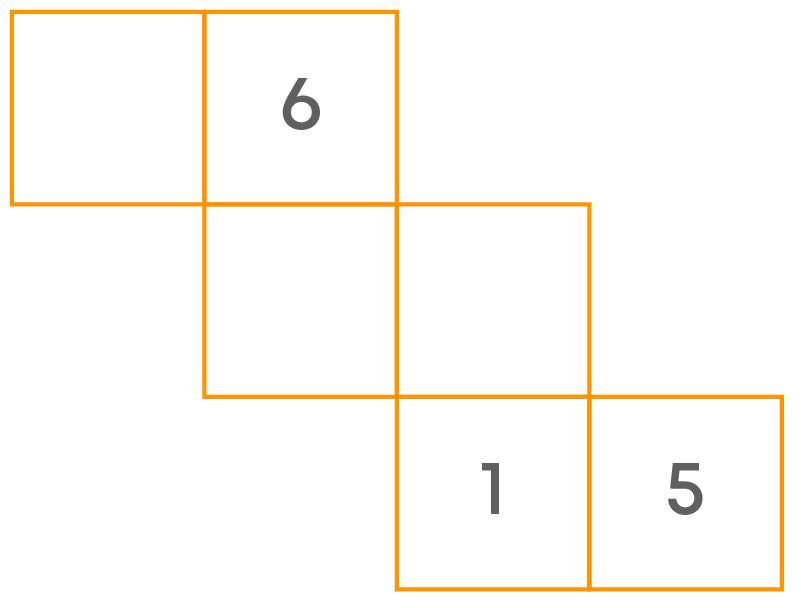
Can you insert the missing numbers so that its opposite faces have a total of seven dots on them?
The given net has the numbers 6, 1, and 5.
- To find the missing numbers, we first determine the pair of opposite faces of the die with the help of given net.
- We find the square that forms a pair of opposite faces with the square having 5.
As adding 2 to 5 gives us 7, the missing number is 2.
- Now as the numbers 1, 2, 5 and 6 are all taken, the only numbers that are left with us are 3 and 4.
The other two blank squares form a pair of opposite faces. Also, the remaining numbers 3 and 4 adds to 7.
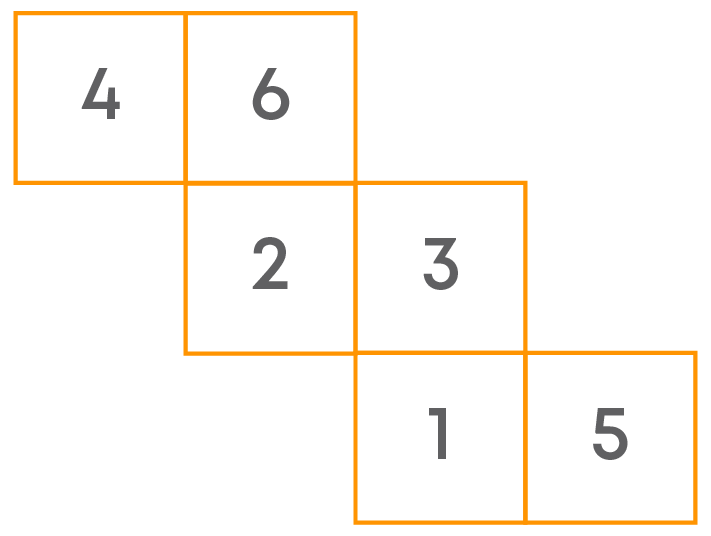
So, we have obtained the positions of missing numbers in the net of given die. There can be two such nets.
Drawing Solids
A net is a 2-D representation of 3-D solid objects. Is there any other way to represent the 3-D solid objects on a sheet of paper? Have you heard about an oblique sketch?
Given below is the oblique sketch of a 3-D solid (cube) on a square grid paper.
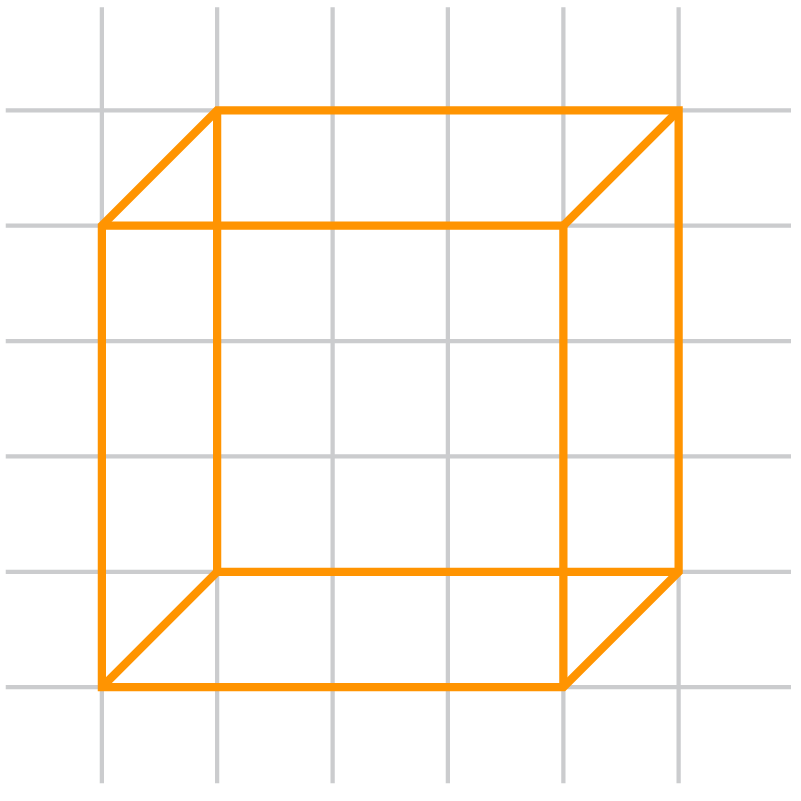
Observe that, in this sketch, the sizes of the front face and its opposite face are same.
Also, the length of each edge drawn is not the same but still it looks like a cube.
Such a sketch is called an oblique sketch. From the above, we can see that:
- An oblique sketch is drawn on a square-grid paper.
- An oblique sketch focuses more on the front face of a 3-D solid shape.
- All the edges of the oblique sketch may not be equal to the dimensions of the given solid.
- An oblique sketch is a 2-D representation of a 3-D solid shape.
Let us draw an oblique sketch of a cube with its each edge 2 units long.
Step 1: First, draw the front face with length of edge 2 units.
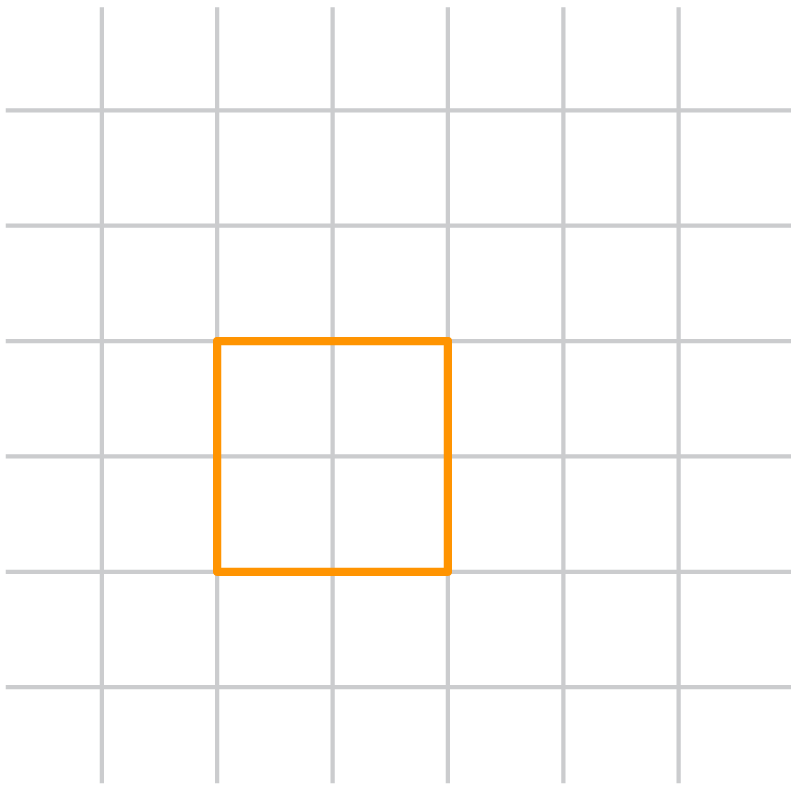
Step 2: We draw the opposite face of the same size which is offset to the front face.
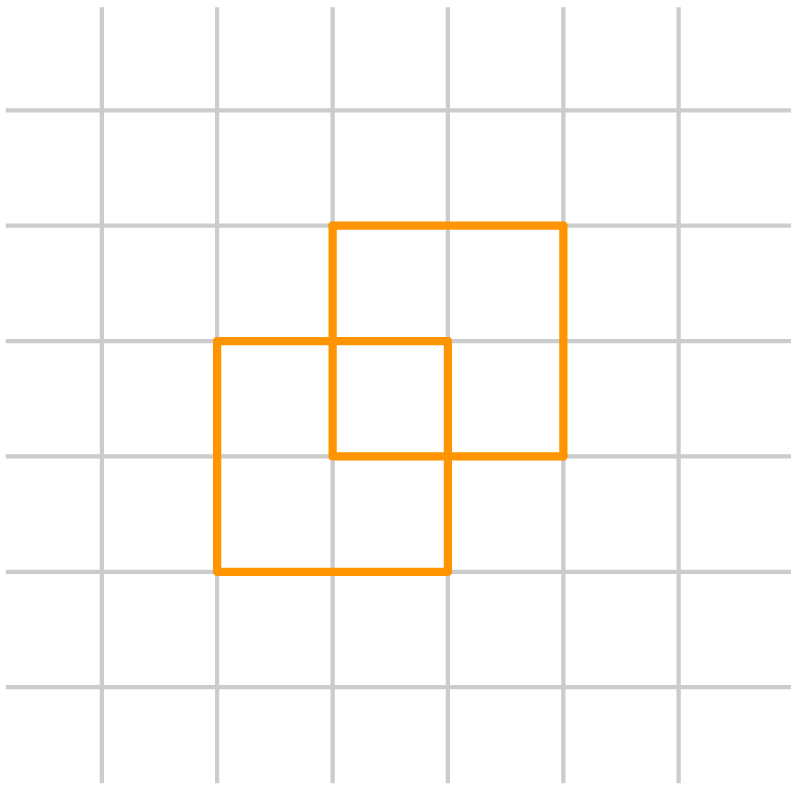
Step 3: Now, we join the respective vertices, to form a cube.

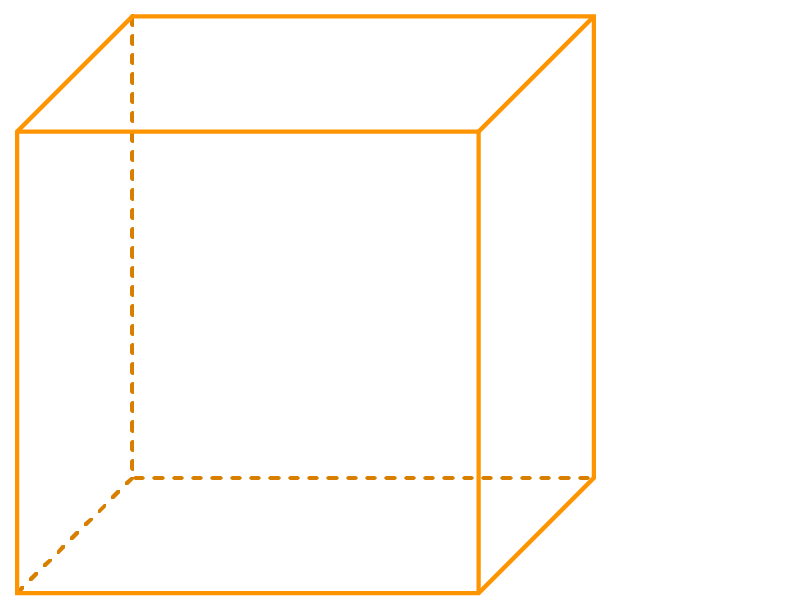
Step 3: Now we redraw using dotted lines for the hidden edges.
The oblique sketch of the cube whose each edge measures 2 units is:
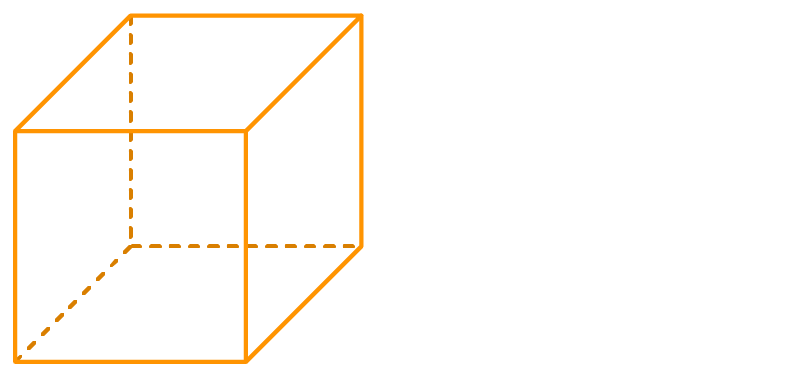
An oblique sketch is used to draw 3-D solid objects on a plane of paper. An oblique sketch focuses more on the front face of 3D solid shape.
You know how to draw an oblique sketch of a 3-D solid. Another method of representing an 3-D solid on a 2-D sheet of paper is an isometric sketch. This is done using an isometric dot sheet.
Let us understand what an isometric dot sheet is.
A sheet dividing the paper into small equilateral triangles made up of dots is known as an isometric dot sheet.

To represent 3-D solid objects on a 2-D plane of paper, such isometric dot sheets are used.
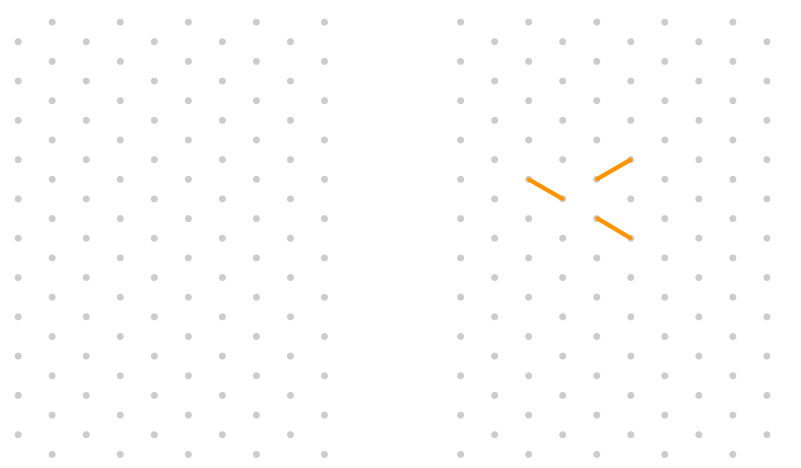
In an isometric dot sheet, the distance between two dots shown is considered 1 unit.
So, when we say draw a line of 3 units the dots can be joined to get 3 units using slant lines shown below:
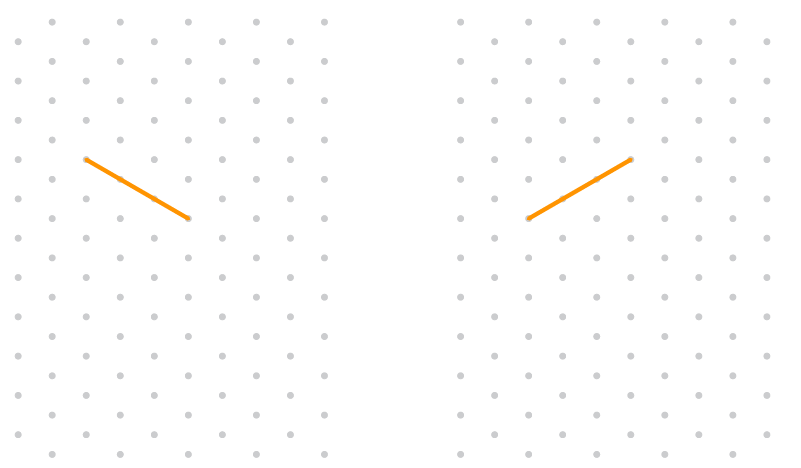
Consider the sketch below of a 3-D solid (cube) drawn on an isometric dot sheet.
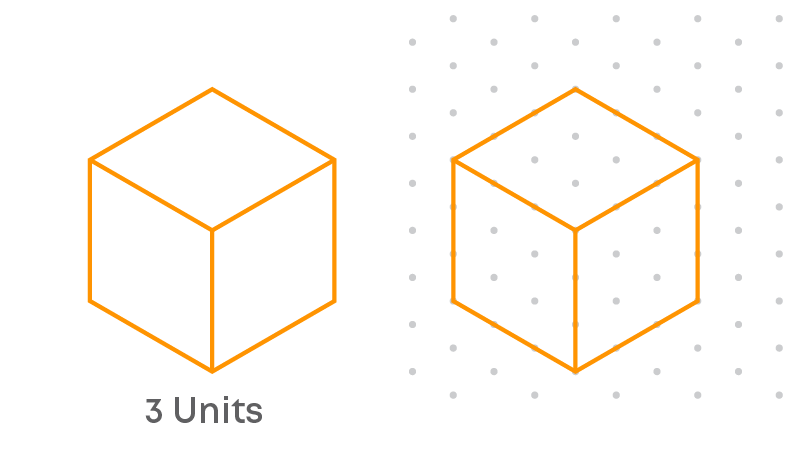
The edges of each face are drawn by joining the dots using slant lines to get 3 units. So, the measurements of the sketch are proportional to that of the 3-D object (cube). Such a sketch is called an isometric sketch.
Let us draw an isometric sketch of the cuboid with the help of its oblique sketch given below.
The dimensions of the cuboid are 8 units × 4 units × 2 units.

Step 1: Take an isometric dot paper.
Step 2: To draw the front face, join dots to form the length of the cuboid 8 units and adjacent dots to form its breadth of 4 units.

Step3 : From the vertices of the face drawn in step 2, draw 4 parallel line segments 2 units long.

Step 4: Join the vertices using appropriate line segments

Step 5: This is the isometric sketch
Visualising Solid Shapes
Consider the shape of the box shown below.

Can you identify the shapes which are combined to form the shape of the box?

Do you observe that the lower part of the box is of the shape of a cuboid? What about the shape of the upper part?

It is half of a cylinder. So, here a cuboid and a half of a cylinder form the shape of the box.
In our daily life, we find some objects which are combinations of different solid shapes. Two or more solid shapes combine to form another solid. To identify different shapes making a given solid, try to split the given solid into known shapes.
Viewing Solids
You might have seen different fruits cut into halves. Have you ever noticed the shape of the surface of a cut piece of any fruit? Let us consider a watermelon.

Now, let us cut it as shown below.

What is the shape of the surface of each cut piece?

Isn’t it circular? Yes, each half of the watermelon has the surface of a circular shape. We call this surface a ‘cross-section’ of the watermelon.
Can we cut a watermelon in any other manner?

What is the shape of the surface of each half now? Is it circular?

Do you notice that the boundary of this cross-section is a plane closed curve? But it is not circular.

Thus, the cross-section of an object will have different shapes depending on the way of cutting.
When an object is cut vertically or horizontally, the flat surface of each cut piece is called a cross-section of the object.
Let us see the cross-sections of different three-dimensional shapes.
CROSS-SECTION OF A TRIANGULAR PYRAMID
Consider a triangular based pyramid.
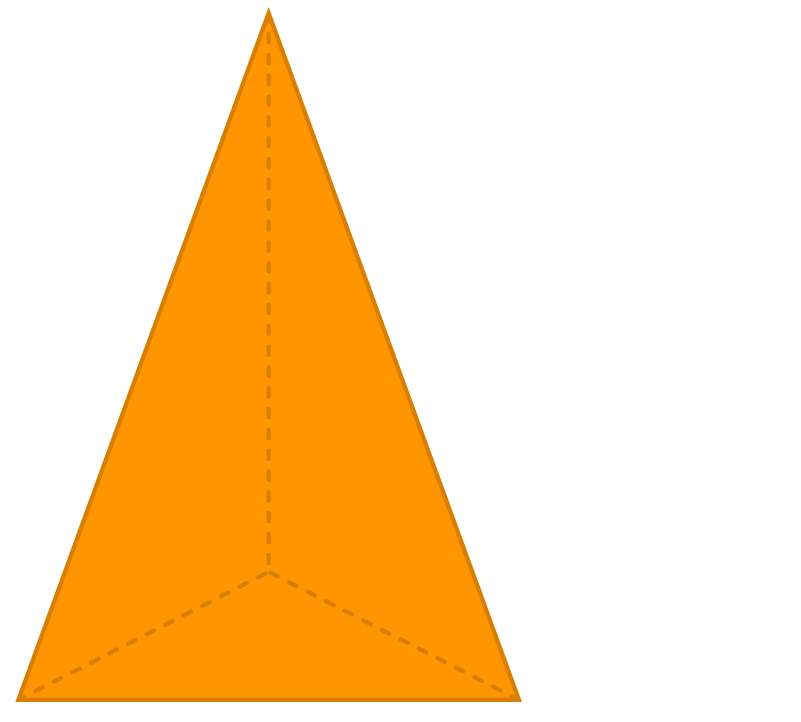
Let us see what the shape of the cross-section will be when it is cut vertically.


What is the shape of the cross-section? It is a triangle.
CROSS-SECTION OF A SQUARE PYRAMID
Now, let us check the cross-sections of a square pyramid.



We can see that we get cross-sections of the shapes - square, trapezium and triangle by cutting the pyramid in different ways.
CROSS-SECTION OF PRISMS
Similarly, we can see different shapes of cross-sections of prisms.
We observe that depending on the shape of a solid and the way of cutting the solid, the shape of the cross-sections varies.
Remember, for a given shape of cross-section, there may be more than one solid shapes.
Have you played the game of creating different creatures with the shadow of hand postures?
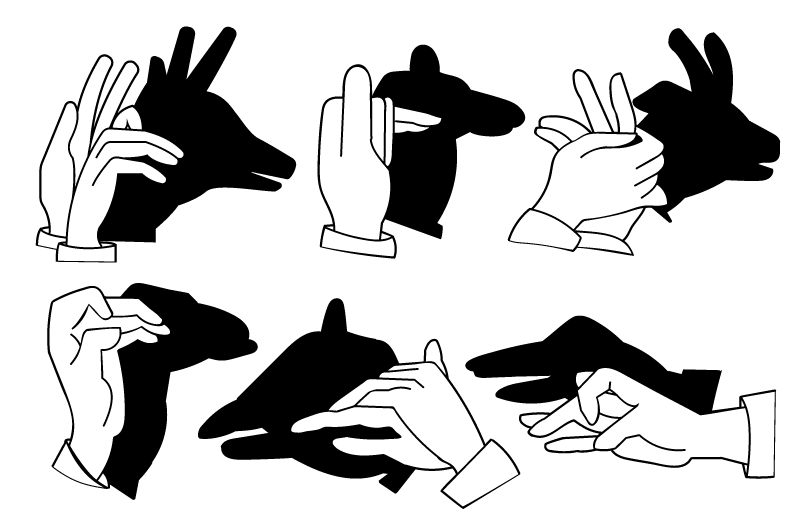
Here, the hand is three-dimensional, but the shadow cast is two dimensional. Similarly, we get the shadow of different three-dimensional objects as two-dimensional shapes.
Let us look at the following examples.
Shadow Of A Sphere
Consider a ball which has a spherical shape.

We know that it is a three-dimensional shape. Now, let us get its shadow using a torchlight.

What is the shape of the shadow? It is a circle. If the ball is cut vertically, the shape of the cross-section is also circular.

Shadow Of A Cylinder
Now, let us take a cylinder and get its shadow.

Here, we observe that the cylinder is kept vertically. Now, let us get the shadow by keeping the cylinder horizontally.

Thus, we observe that,
- The shape of the shadow of the cylinder is rectangular when the cylinder is kept vertically in front of torchlight.
- The shape of the shadow of the cylinder is circular when the cylinder is kept horizontally in front of torchlight.
It is similar in case of the cross-sections of the cylinder. When it is cut vertically, the cross-section is rectangular and when it is cut horizontally, the cross-section is circular.
A solid can look different from different angles of view. The front-view, the side-view and the top-view can provide a lot of information about the shape observed. It tells about the shape of the solid or the shapes of different solids combined if it is a combination of two or more solid shapes.
Now, let us consider the following solid made up of cubes.

Let us see how it looks from different angles of view. How does it look from the front?
If you look at the solid from the front, you can see 3 cubes arranged vertically and 3 cubes horizontally as shown below.

So, this is the front view of the solid. If you look at the solid from a side, you can see 3 cubes arranged vertically as shown below.

So, this is the side view of the solid. If you look at the solid from the top, you can see 3 cubes arranged horizontally as shown below.

So, this is the top view of the solid. Hence, we can say that a solid can look different from different angles of view.
Any solid shape has three dimensions. Hence, it can have different angles of views. Consider a car. We can observe here that the same car can look different from different angles of view.

Consider the following solid which is a combination of three cuboids.

Let us see its front view, side view and top view.
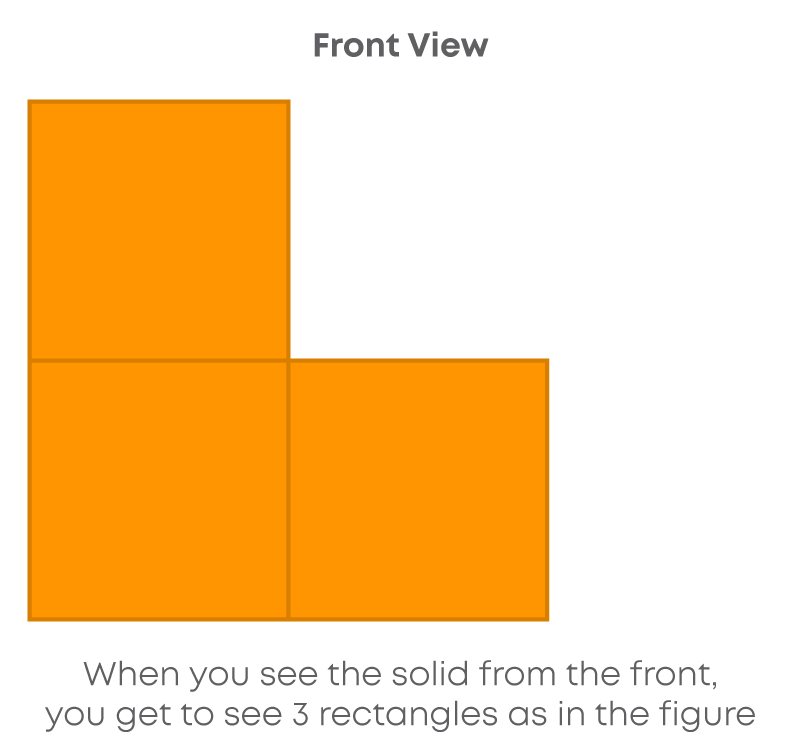

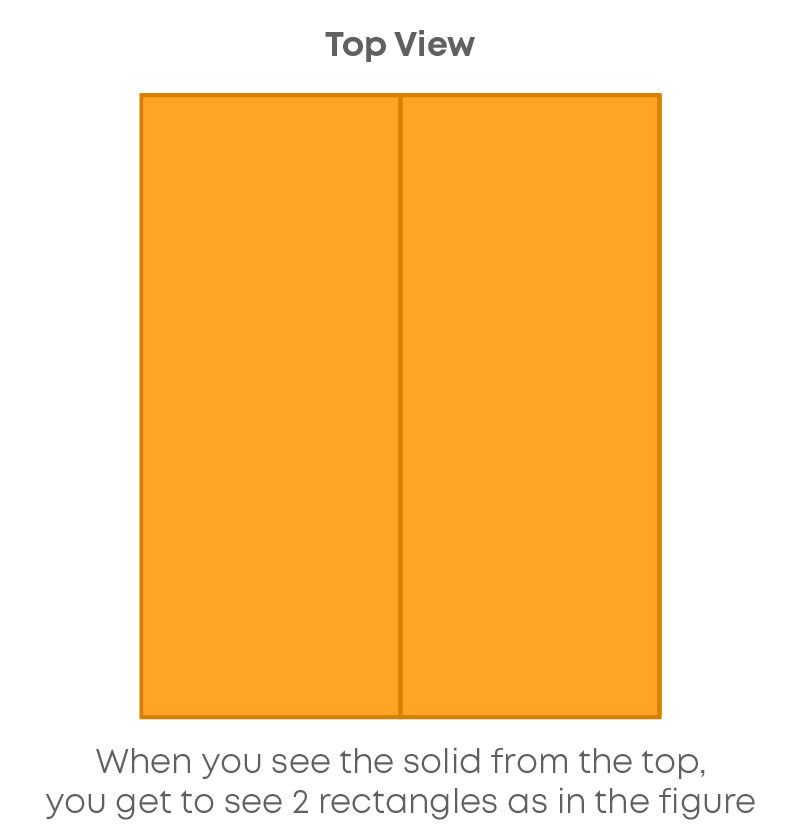

Consider the following solid formed using cubes.

This is the front view of the solid. How many cubes can you see here? There are 6.
Now, we will change the angle of view.

This is the side view of the solid. How many cubes can you see here? There are 2.
Now, we will see the solid from the top.

This is the top view of the solid. Here, we can see 4 cubes.
From the side view of the solid, we can see that the solid has only one column of cubes. So, whatever is visible from the front view, gives the number of cubes involved in the solid.
So, by collating all the views, we can observe that the solid has 6 cubes in total.
Common Errors
The following are topics in which students make common mistakes when dealing with visualising solid shapes:
- 1. A cube does not have only one net
- 2. Identifying nets of a die
- 3. Identifying the different views of a solid
A Cube Does Not Have Only One Net
There can be a number of nets for a cube. Remember! A net of a cube is an outline when folded forms a cube. So, it should be made up of 6 squares only.
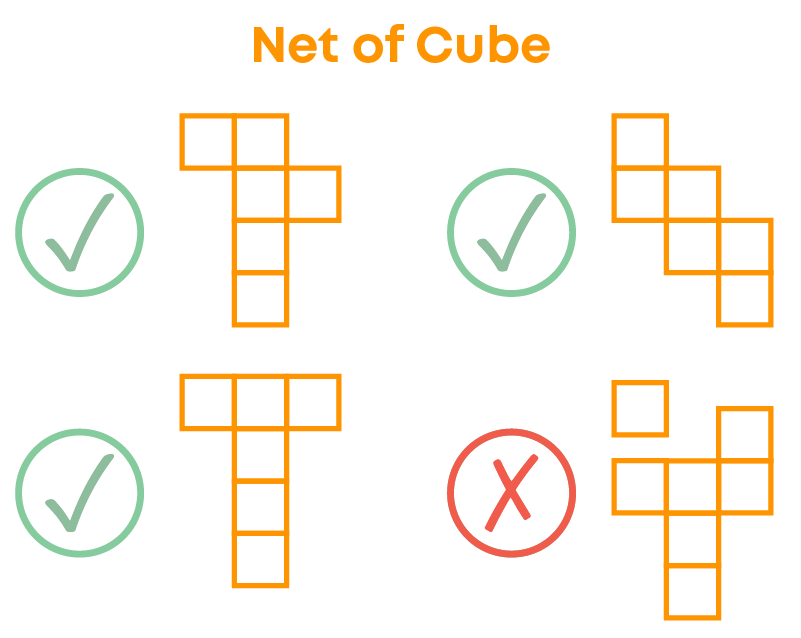
Identifying Nets Of A Die
There can be a number of nets for a die. Remember! A net of a die is an outline when folded forms a die such that:
1.It has 6 squares.
2.The numbers on the opposite faces add up to 7.
This is the net for a die as the numbers on the opposite faces add up to 7:
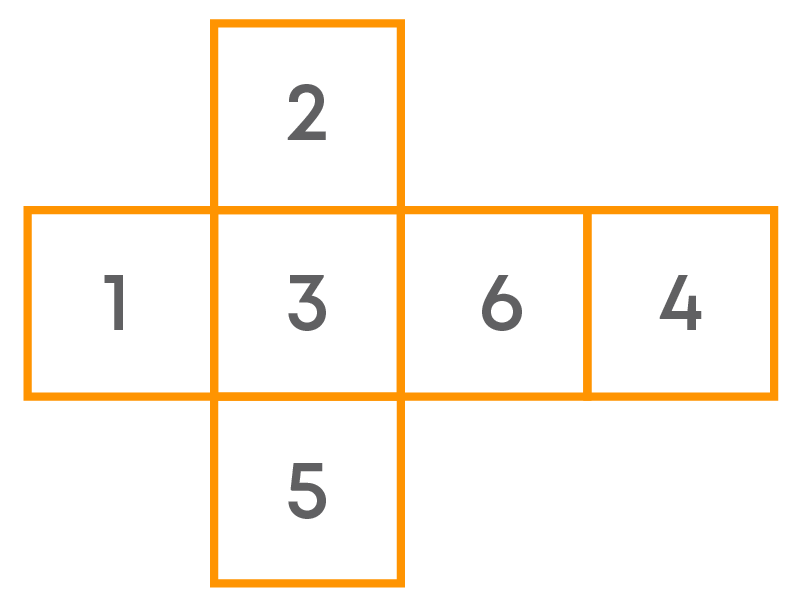
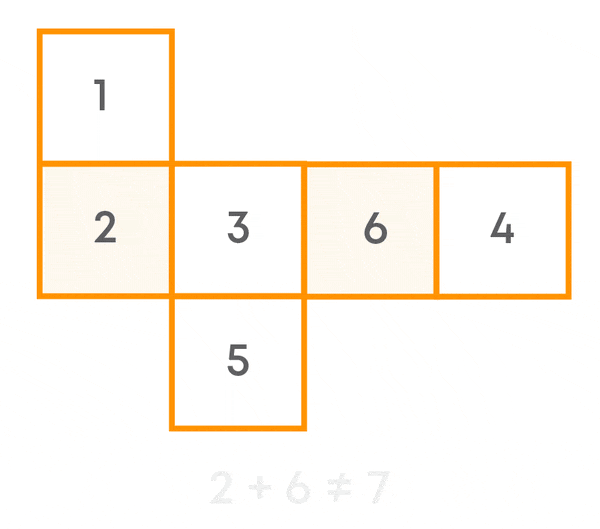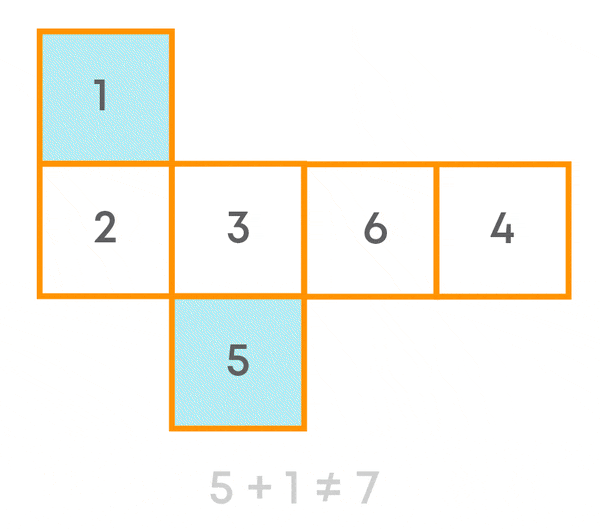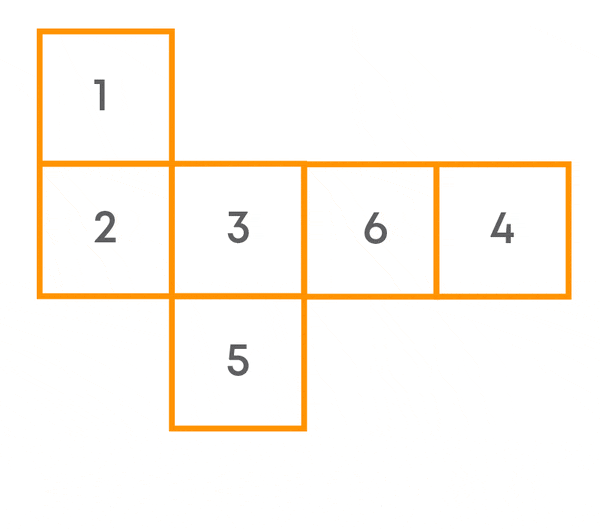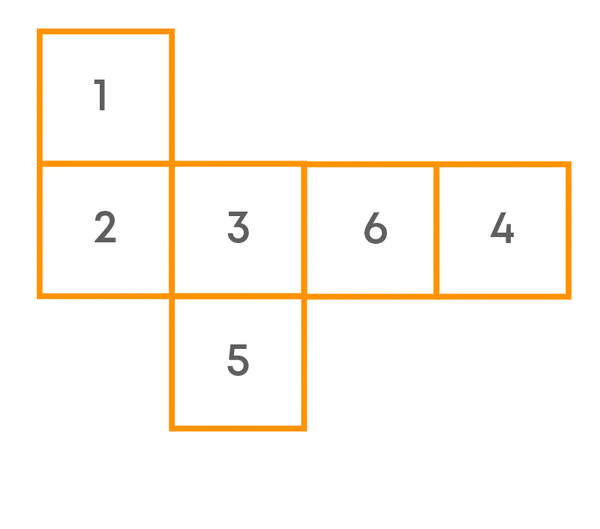
This is not the net for a die as the sum of the two numbers on the opposite faces is not always 7:
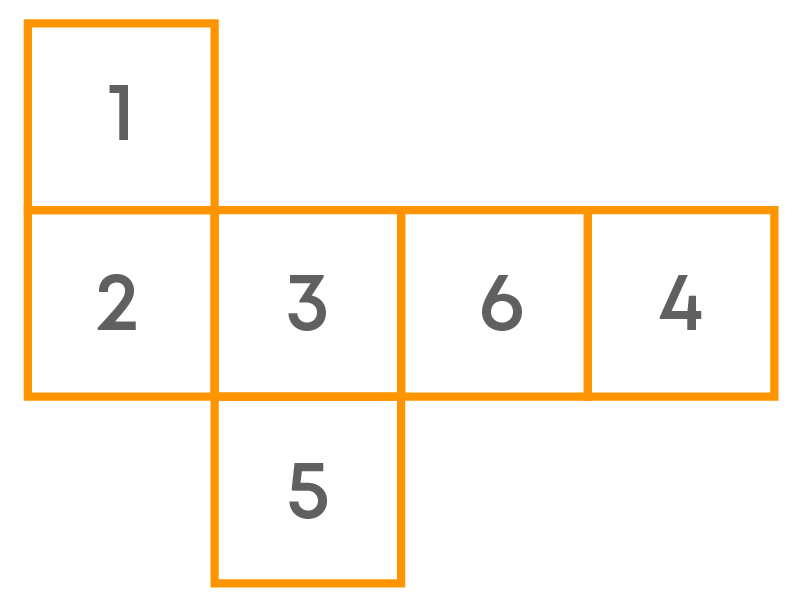
This is not the net for a die as the two faces have the same number 1:
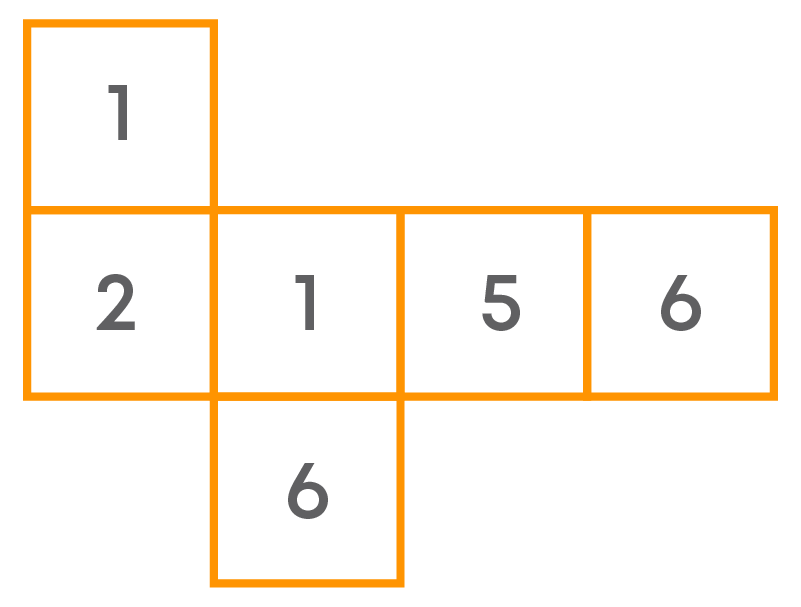
This is not the net for a die as some faces overlap each other:

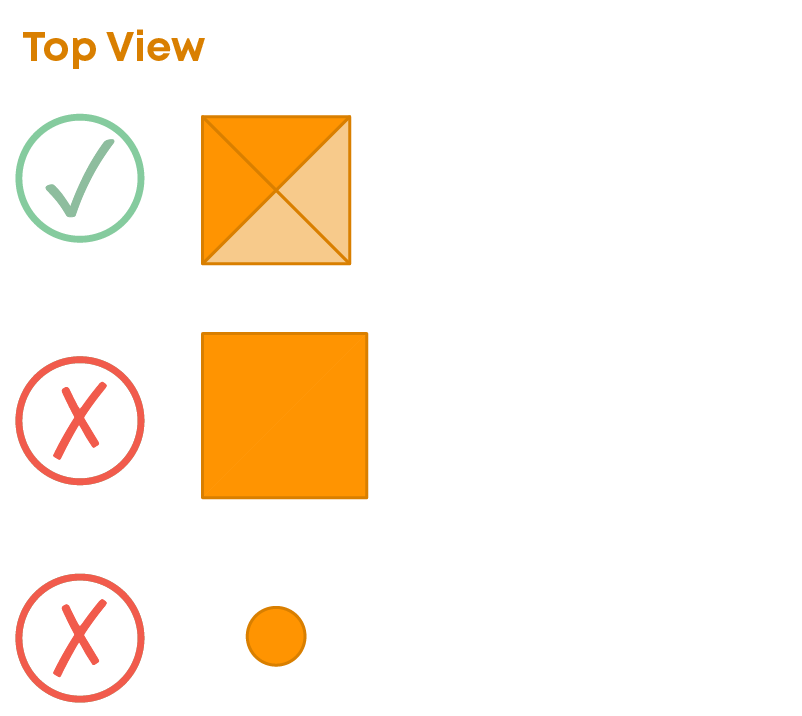
Identifying The Different Views Of A Solid
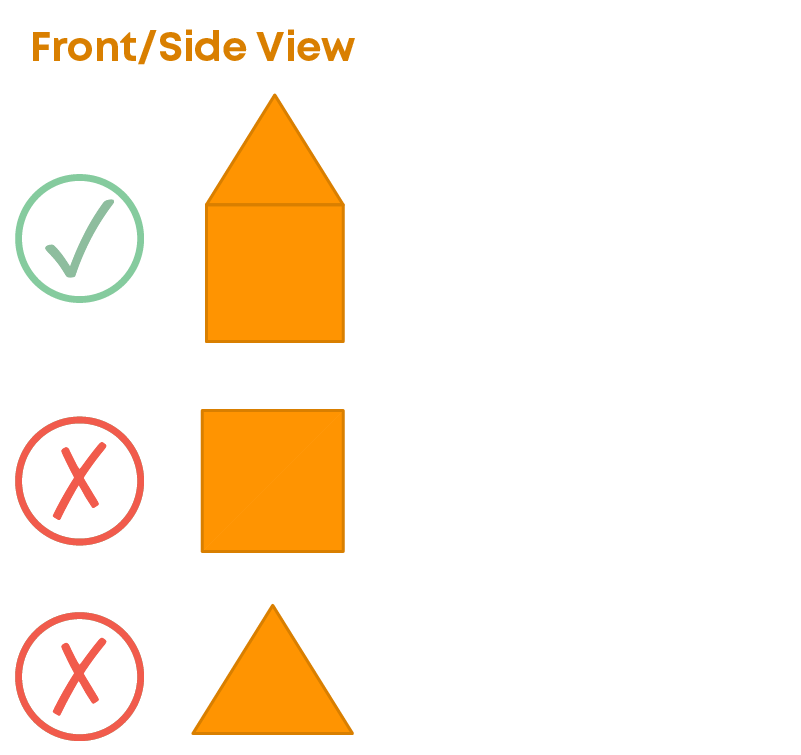
To identify the different views of a solid shown below, imagine how it looks from the top, side and front.

Remember! When the solid is seen from the top, you get to see a square containing four line segments in it, not a single dot or square.

When the solid is seen from a side, the solid will look the same as in the front view, we can see a combination of a triangle and a square, not only a square or a triangle.

Conclusion
Solve the riddle below after you are thorough with visualising solid shapes:
How many cubes can you count in the picture below?





















































