Introduction
Practical geometry is a branch of geometry in which we learn the method of constructing various geometrical shapes like line segments, angles, triangles, and different polygons.
We use various geometrical tools to construct the required shapes with the exact measurements given. In practical geometry, we will learn how to construct a given geometrical shape with certain measurements using a ruler, compass, and a protractor.
What is practical geometry and why do we need it? Let us watch this video to know this.
Did you know? Quadrilaterals are an important shape in arts and crafts. Learning how to construct them will help you create basic shapes such as squares, rectangles, kite, etc. Many art and craft projects involve the use of quadrilaterals.

Concepts
The chapter ‘Practical Geometry’ covers the following concepts:
Constructing Quadrilateral
Remember!
- With the same measures of the sides, we can create different quadrilaterals.
- To construct a unique quadrilateral, we need to know another measure such as that of an angle.
So, along with the four sides, it would have been better if we knew the measure of one of the angles to get the quadrilateral we want.
This means, to construct the desired quadrilateral, we need the measurement of at least 5 elements. But in what combination?
The following combinations of elements will be required to construct a unique quadrilateral:
- 1. Four sides and an angle
- 2. Four sides and a diagonal.
- 3. Two diagonals and the given three sides.
- 4. Two adjacent sides and the given three angles.
- 5. Three sides and the two given included angles.
We can also construct special quadrilaterals such as square, rectangle, parallelogram, or rhombus.
Consider the following conditions to construct a quadrilateral DEFG.
The quadrilateral DEFG, should have sides DE = 3.2 cm, EF = 3 cm, FG = 2.8 cm, DG = 2.5 and diagonal DF = 4 cm.
Any problem or situation in Geometry can be represented using a relevant figure. Before we start constructing, we must first represent the given quadrilateral with a figure. This figure should be a close approximation of the required quadrilateral. In other words, it should be a rough sketch of the actual quadrilateral we will be constructing. Let us draw a rough sketch of the quadrilateral DEFG that we must construct.
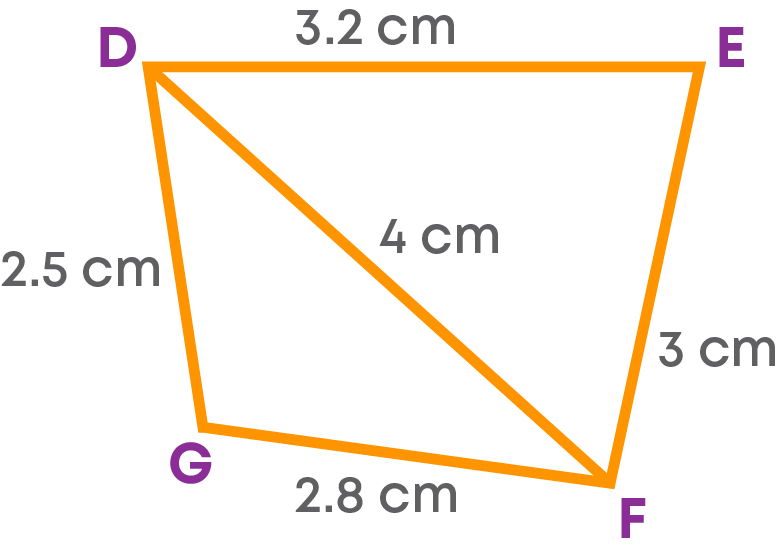
- Draw the given diagonal as a base.
- Construct the triangle that will be formed by the two adjacent sides and the diagonal on one side of the diagonal, using the SSS construction criterion.
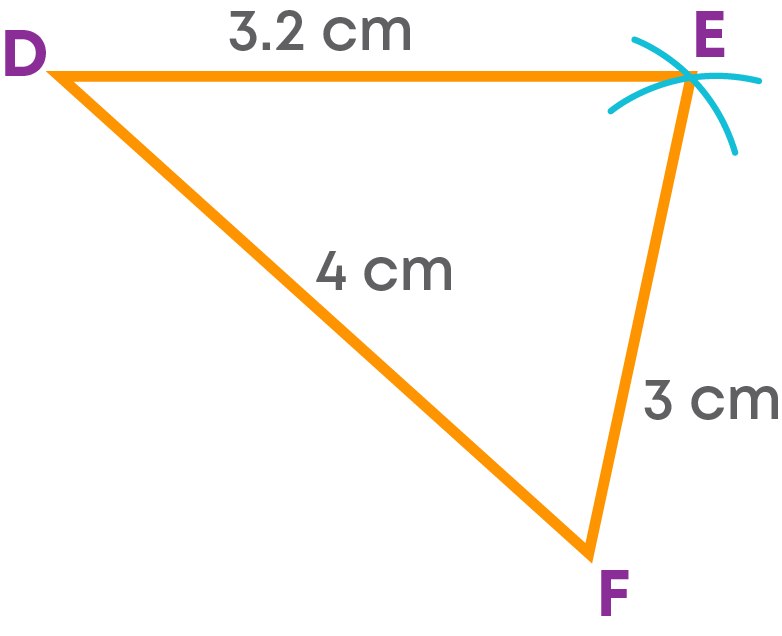
- Next, construct the triangle that will be formed by the other two adjacent sides and the diagonal.
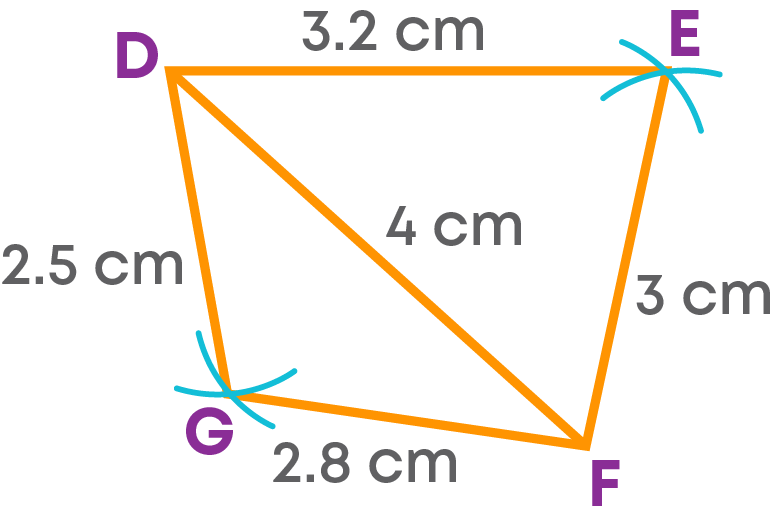
DEFG will be the required quadrilateral.
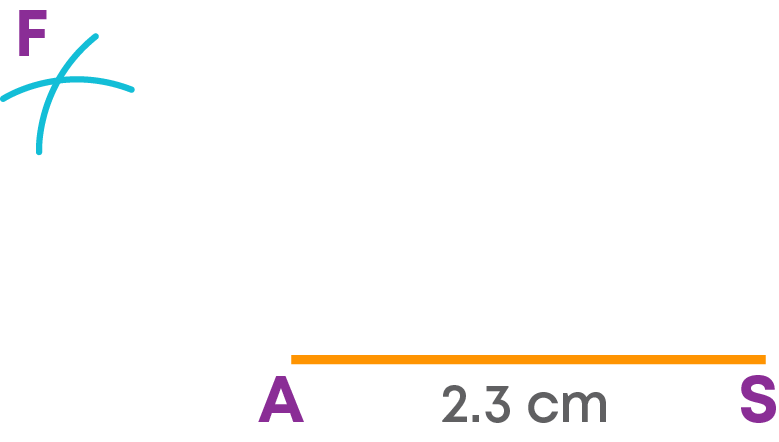
Let us construct a quadrilateral ASDF with AS = 2.3 cm, SD = 2.6 cm, DF = 1.5 cm, AF = 1.8 cm, and SF = 4 cm.
First, let us draw a rough sketch of the required quadrilateral.
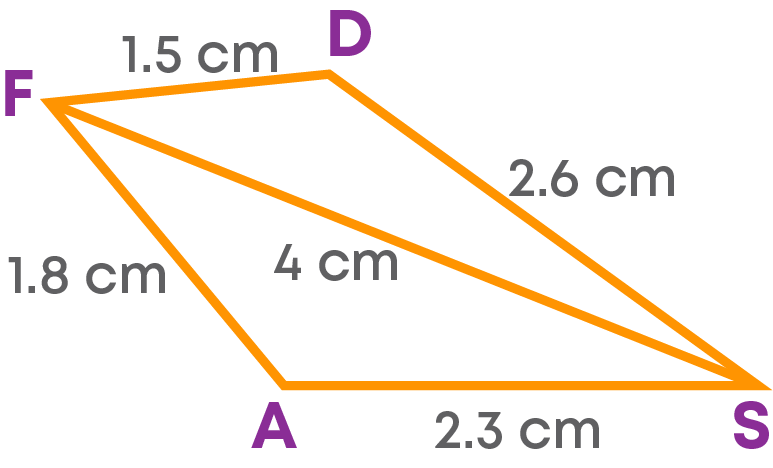
Step 1: Draw the side AS = 2.3 cm.

Step 2: Construct the triangle ASF with AF = 1.8 cm and SF = 4 cm.
- Using a compass, with A as the centre and radius 1.8 cm, draw an arc on one side of AS.
- With S as the centre and radius 4 cm, cut the previous arc at F.
Step 3: Join AF and SF.
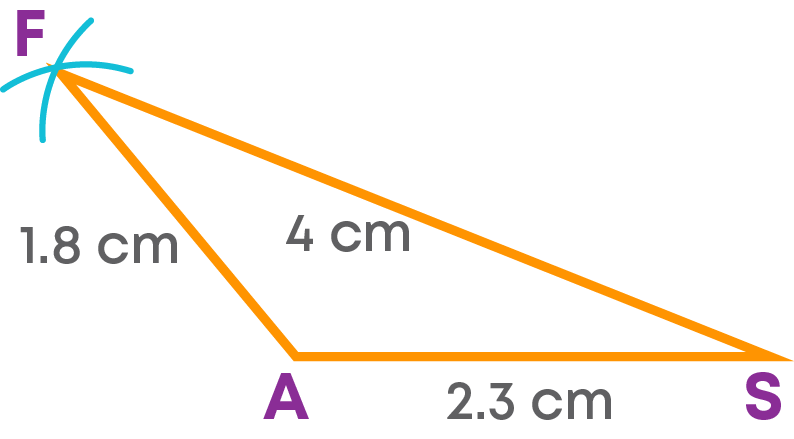
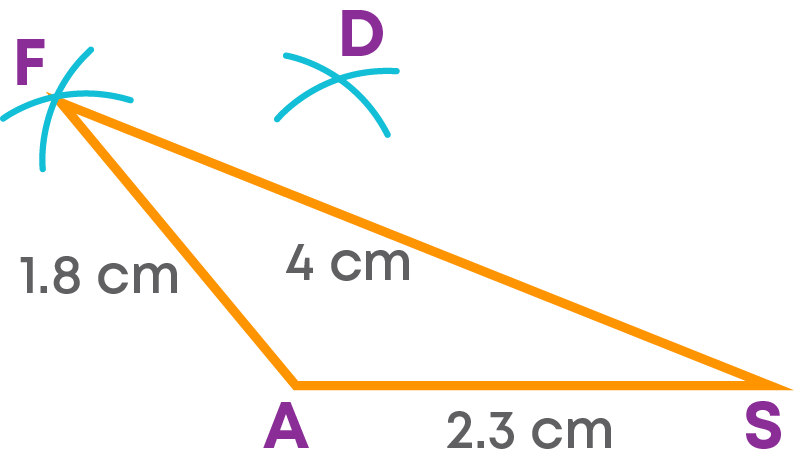
Step 4: Now, construct the triangle SFD.
- With F as the centre and radius, 1.5 cm cut an arc on the opposite side of the triangle ASF.
- With S as the centre and radius 2.6 cm, cut the previous arc at D.
Step 5: Join SD and DF.
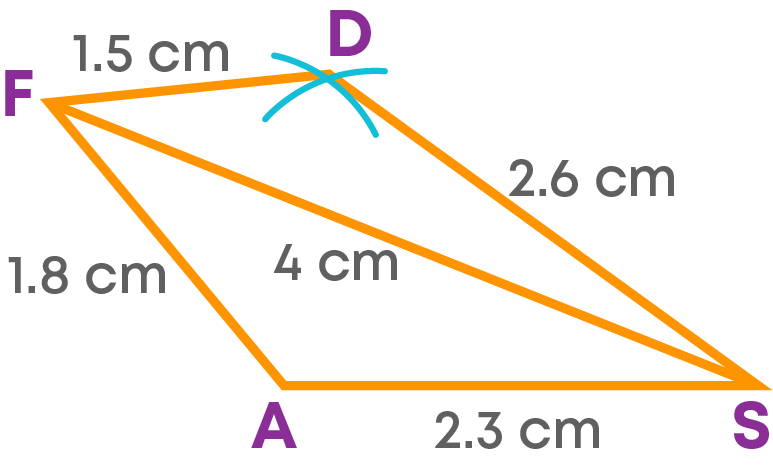
ASDF is the required quadrilateral. Let us see the construction.

How to construct a quadrilateral when the lengths of the two diagonals and the three sides are given?
Construct a quadrilateral ABCD whose diagonal AC = 5 cm, BD = 6 cm and the lengths of the sides AB = 4.6 cm, AD = 4 cm, and BC = 3 cm.
To construct such a quadrilateral:
- We draw a rough sketch of the required quadrilateral.
- From the rough sketch, we see that the two triangles formed by the diagonals can be constructed using the SSS construction criterion.
- Using compass and ruler, we construct the first triangle with one of the sides as the base and the diagonal and the adjacent side as the other sides.
- Next, we construct the second triangle formed by the same base, the second diagonal and the other adjacent side of the base.
- We join the remaining vertices of the quadrilateral.
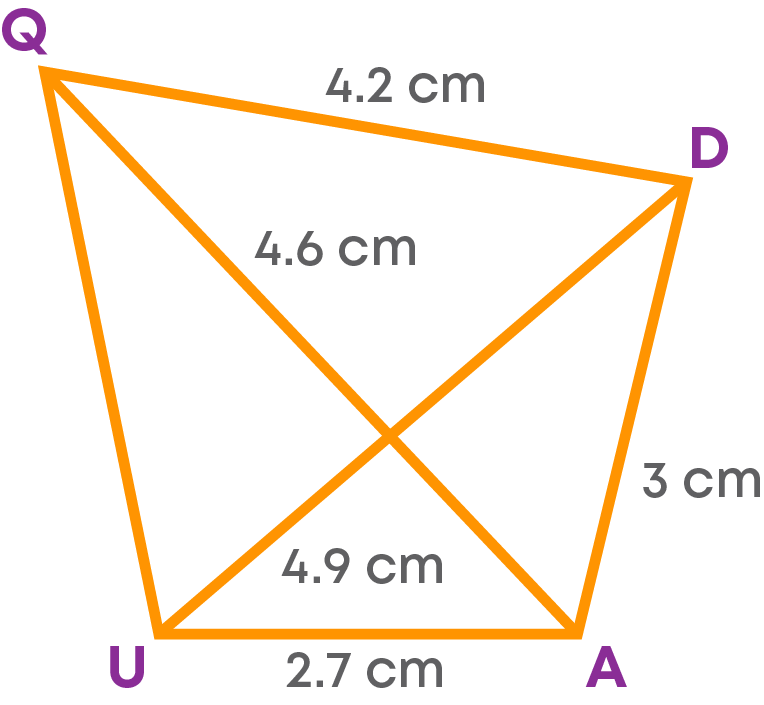
Example: Construct a quadrilateral QUAD with UA = 2.7 cm, AD = 3 cm, QD = 4.2 cm, QA = 4.6 cm and UD = 4.9 cm.
Rough sketch of the required quadrilateral:
Steps to construct the quadrilateral:
Step 1: Draw the side UA = 2.7 cm.
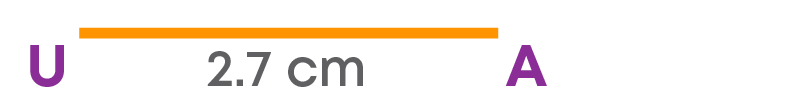
Step 2: Construct the triangle UDA with UD = 4.9 cm and CD = 3 cm.

Step 3: Construct the triangle QDA with QA = 4.6 cm and QD = 4.2 cm.
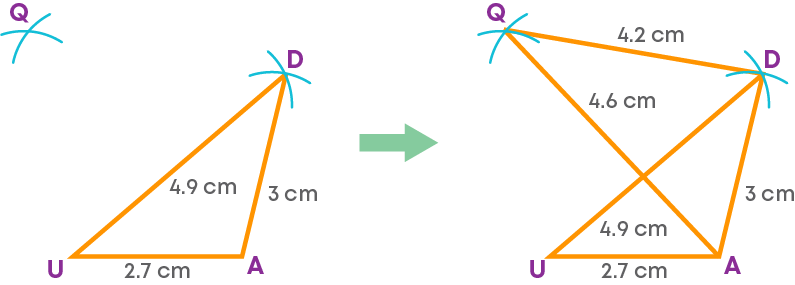
Step 4: Join the vertices Q and U.
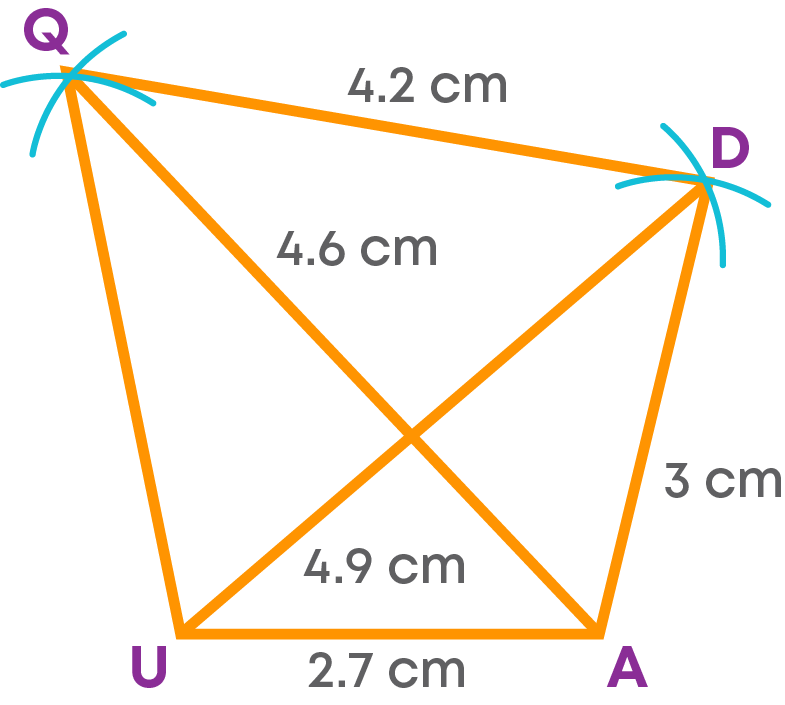
QUAD is the required quadrilateral.
Let us learn how to construct a quadrilateral when the lengths of its four sides and the measure of an angle are given:
Construct the quadrilateral ZXCV with ZX = 3.6 cm, XC = 2.5 cm, CV = 2.8 cm, ZV = 3.2 cm and ∠V = 110⁰.
First, we must draw the rough sketch of the required quadrilateral.
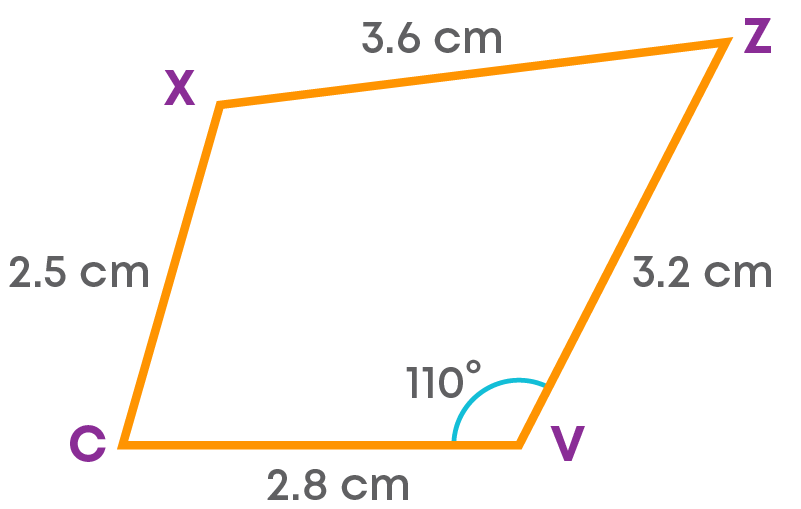
Let us consider CV as the base.
- Step 1: Draw the side CV = 2.8 cm.

Step 2: Using a protractor, draw an angle CVP = 110°, at V.
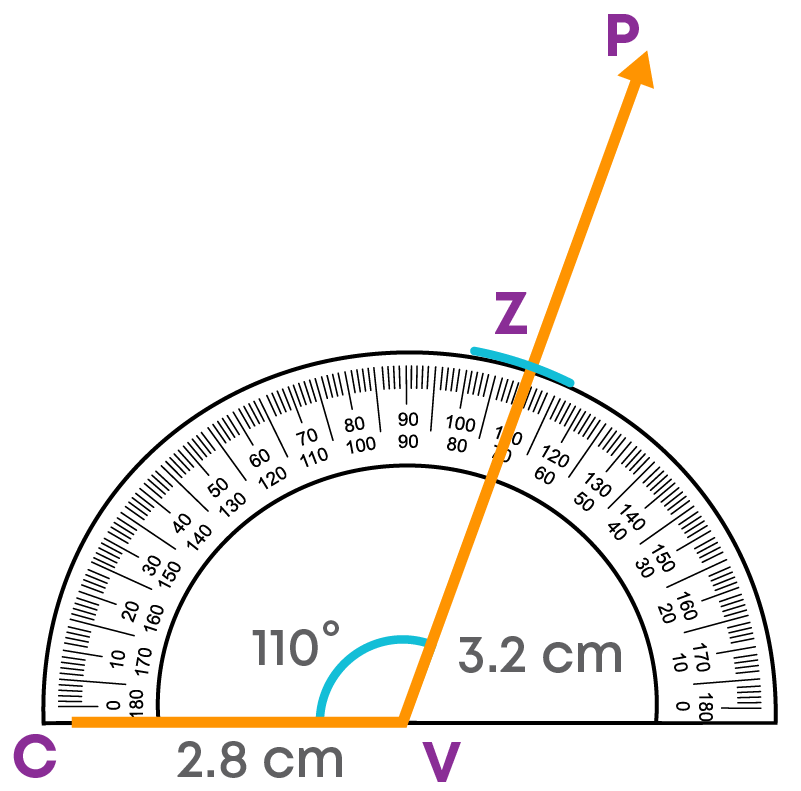
Step 3: With V as the centre and a radius of 3.2 cm, cut off a length of 3.2 cm on VP at Z.
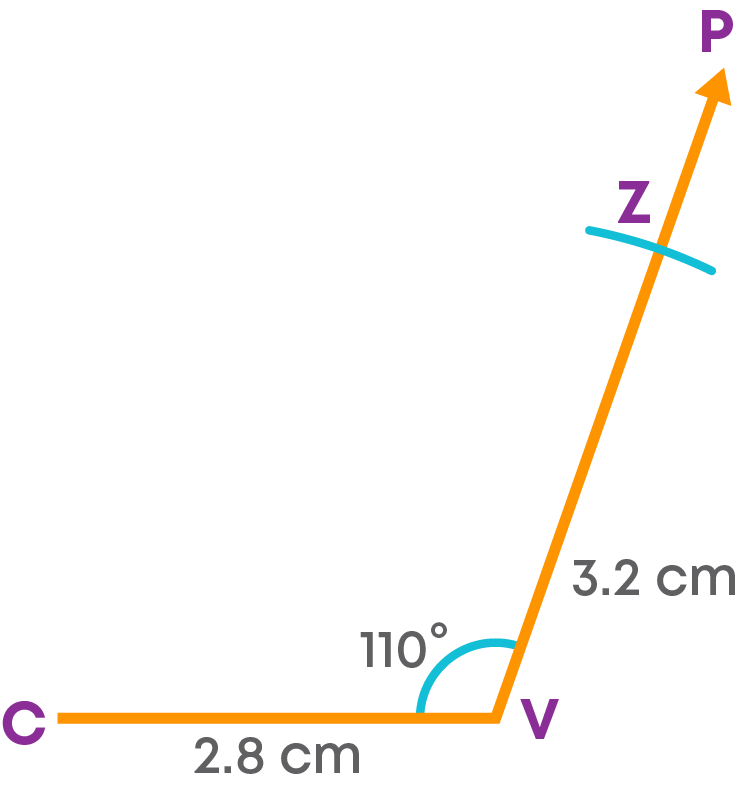
Step 4: With Z as the centre and radius 3.6 cm, draw an arc. Next with C as the centre and radius 2.5 cm, cut the arc drawn at X.
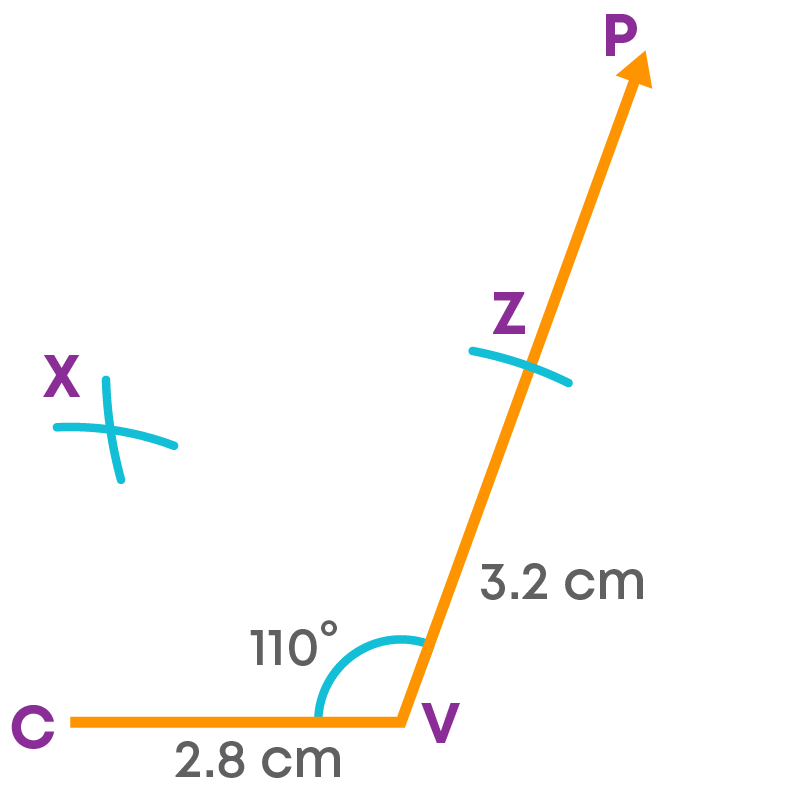
Step 5: Join ZX and CX.
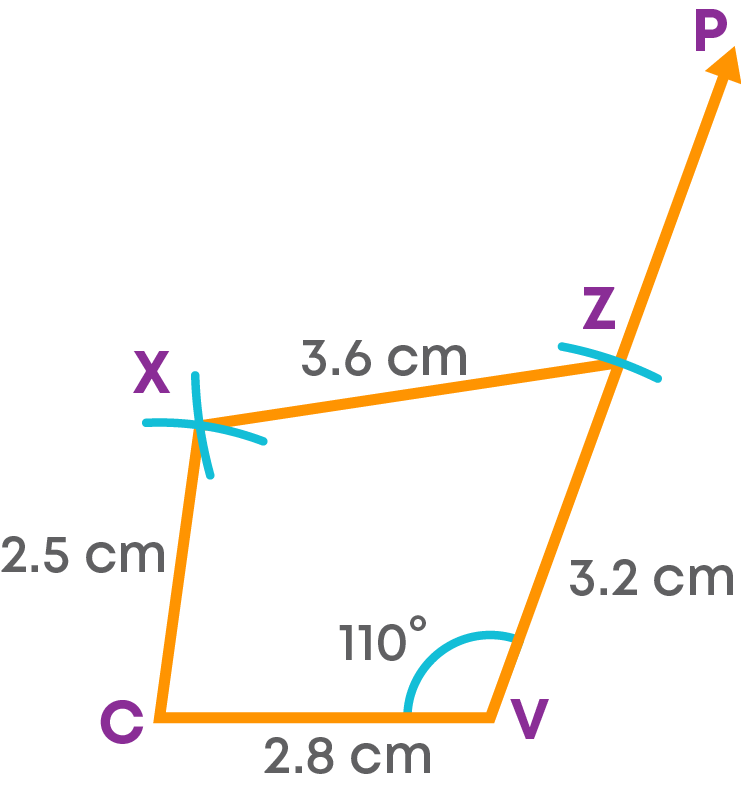
ZXCV is the required quadrilateral. Let us see the steps of construction.

Let us see how to construct a quadrilateral when the lengths of its two adjacent sides and the three angles are given.
Construct a quadrilateral EFGH with EF = 3 cm, EH = 3.5 cm, ∠E = 50⁰, ∠F = 110⁰, ∠H = 85⁰.
The rough sketch of the quadrilateral is:
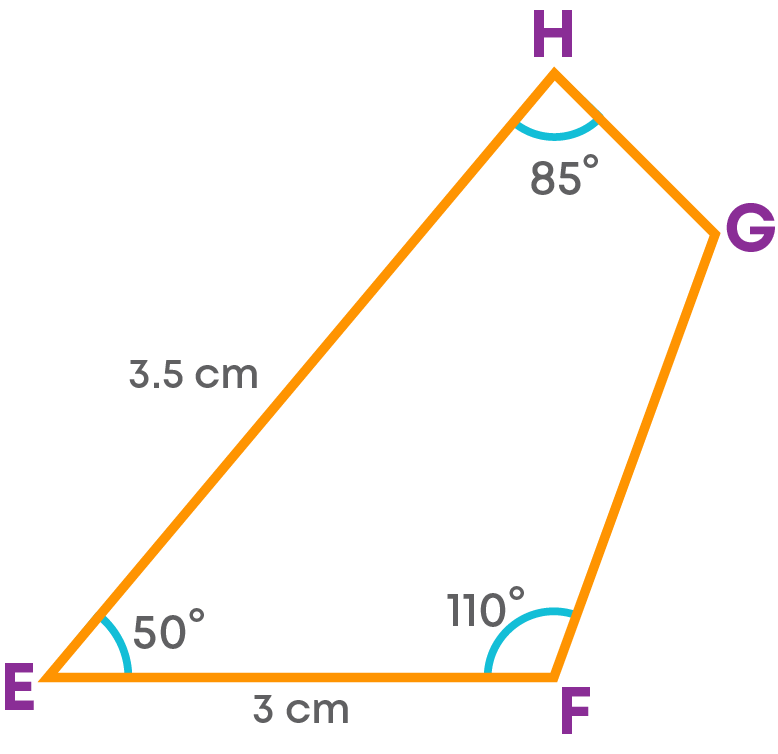
Step 1: Draw the side EF = 3 cm.
We choose this side as we know the measure of the angle at F and the length of the side EF.

Step 2: Draw an angle at E.
Draw angle XEF = 50⁰ at E.
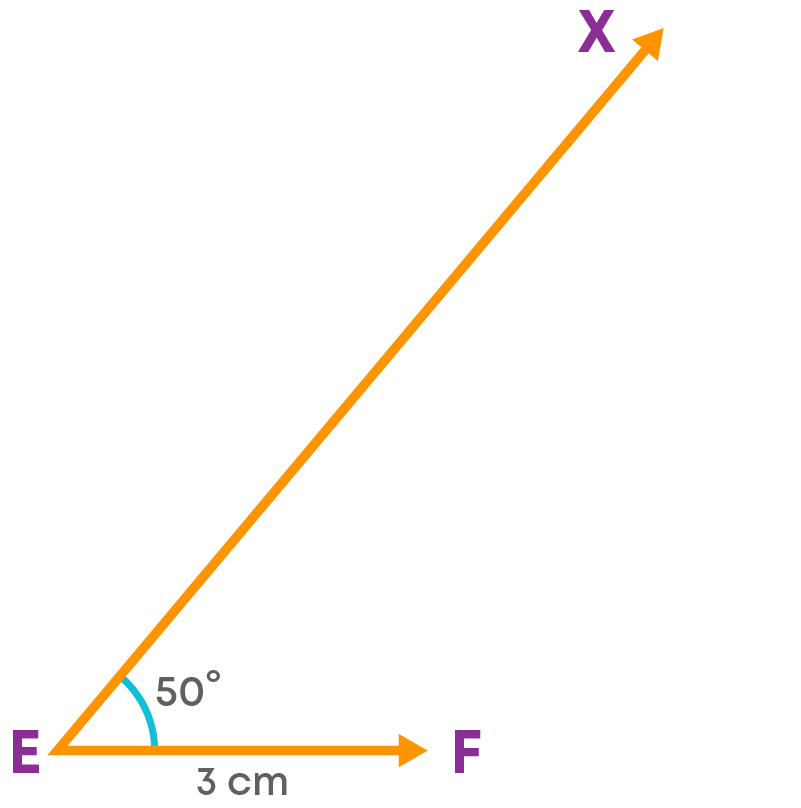
Step 3: Using the compass, cut off a length of 3.5 cm on EX at H.
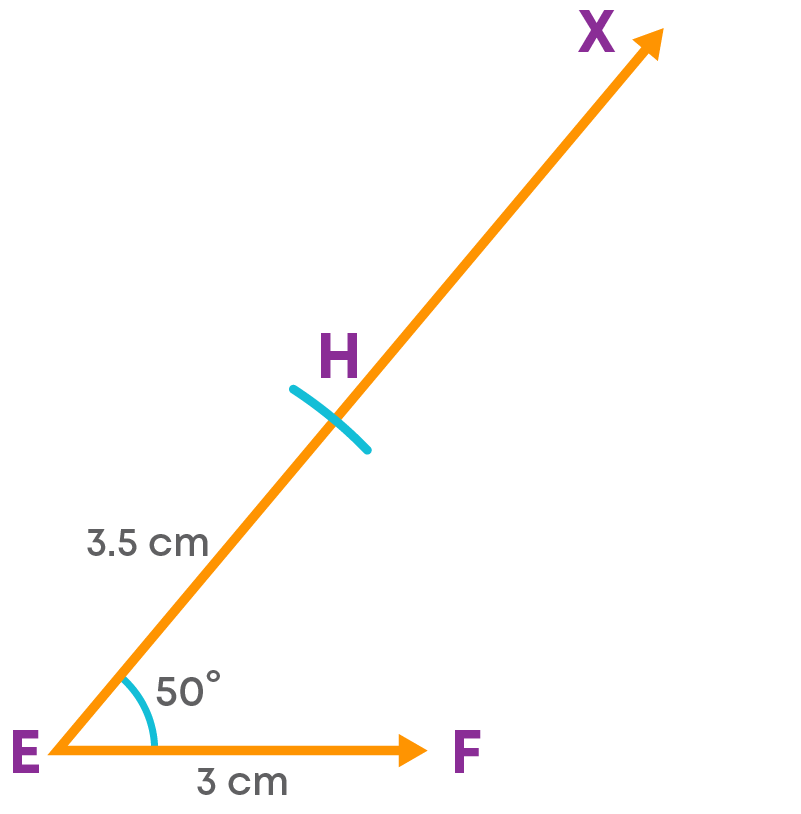
Step 4: Draw an angle at F.
At F, draw an angle EFY = 110⁰.
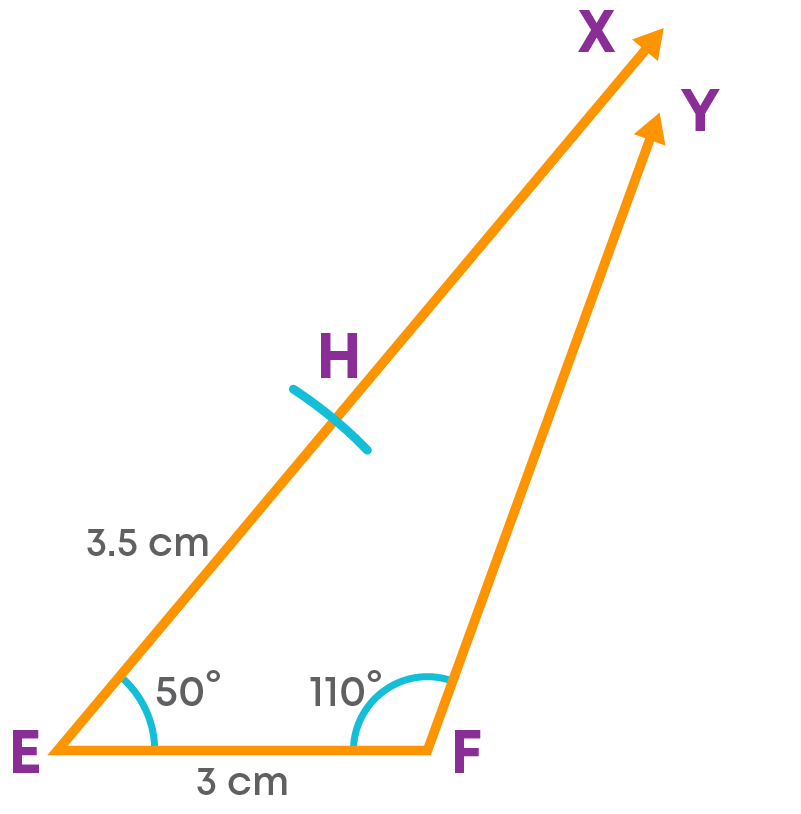
Step 5: With EH as the base, draw an angle of 85° at H.
Extend the arm of this angle to intersect FY at G.
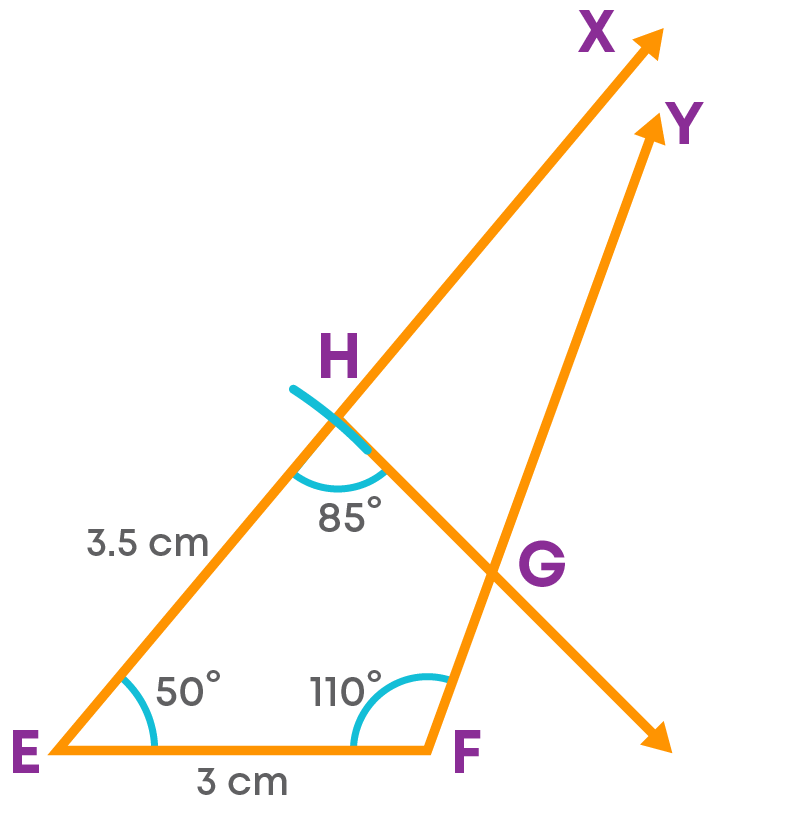
EFGH is the required quadrilateral.
Let us see the steps of construction.

Now, let us construct a quadrilateral when three sides and two included angles are given.
Construct a quadrilateral RGUH with GU = 4 cm, UH = 4.5 cm, RG = 3.8 cm, ∠RGU = 135⁰ and ∠GUH = 75⁰.
Let us construct quadrilateral RGUH:
- First, we draw the rough sketch of the required quadrilateral.
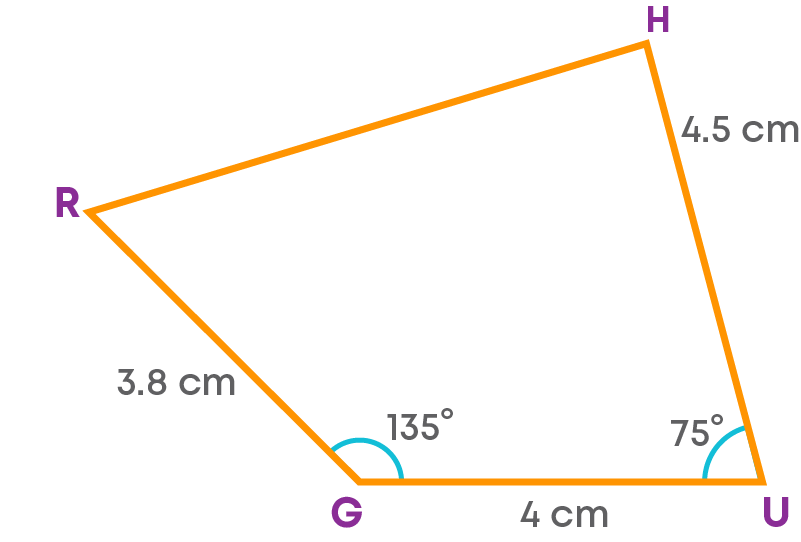
Steps of construction are as follows:
- Step 1: Draw side GU = 4 cm. At G, draw an angle ∠YGU = 135⁰ using a protractor or construct the angle using a compass.
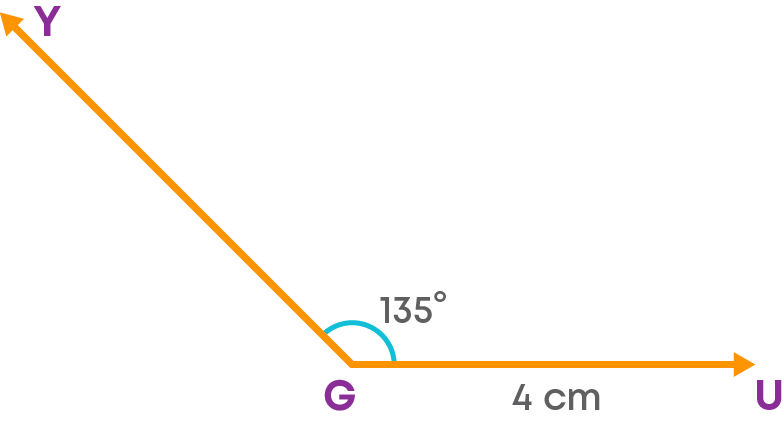
- Step 2: With G as the centre and a radius of 3.8 cm, cut off an arc on YG at R.
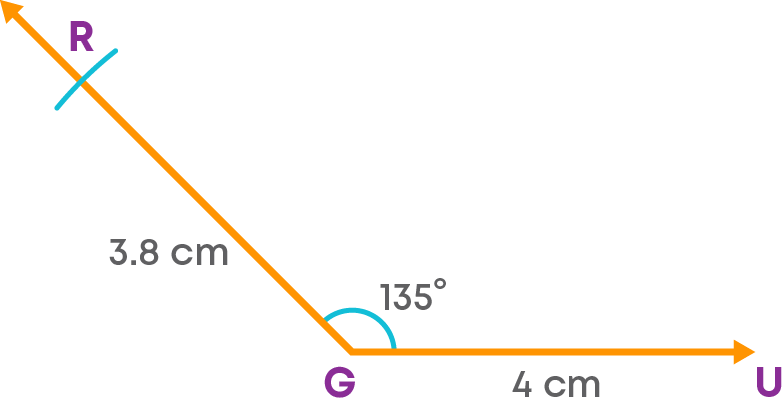
Step 3: At U, draw an angle GUZ = 75⁰.
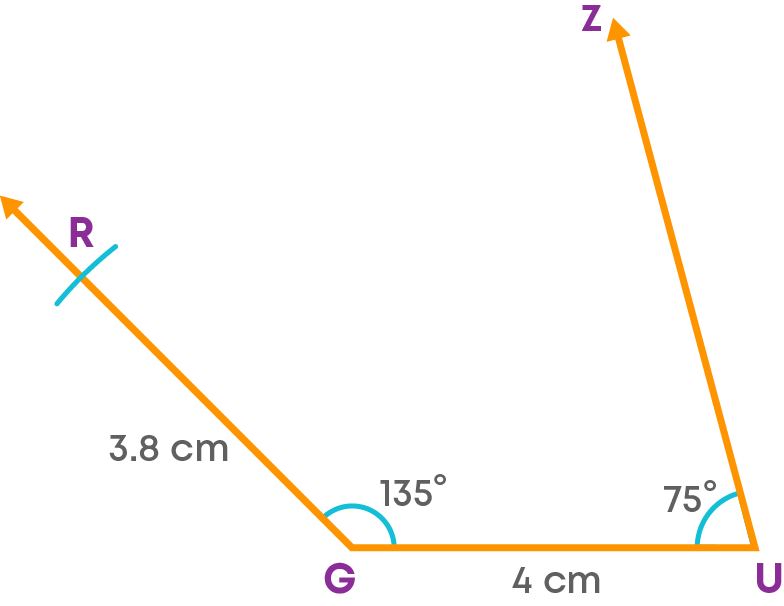
Step 4: With U as the centre and a radius of 4.5 cm, cut off an arc on UZ at H.
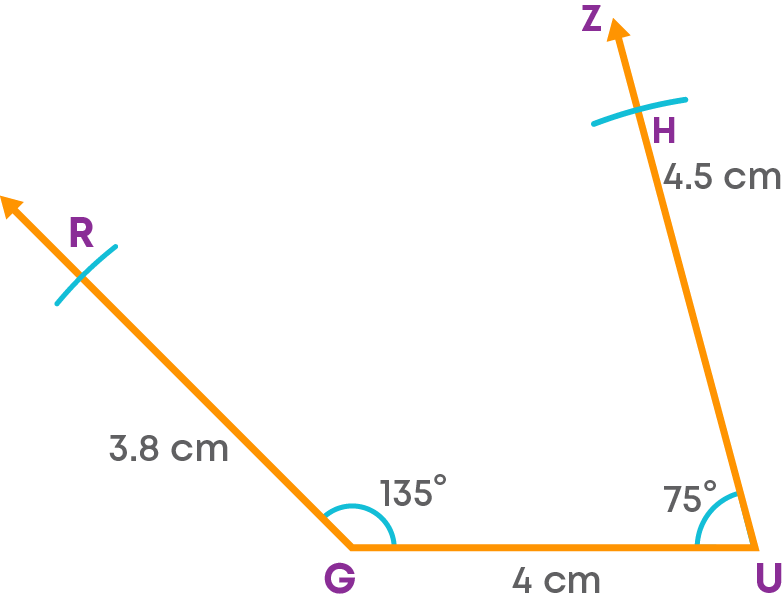
Step 5: Join R and H.
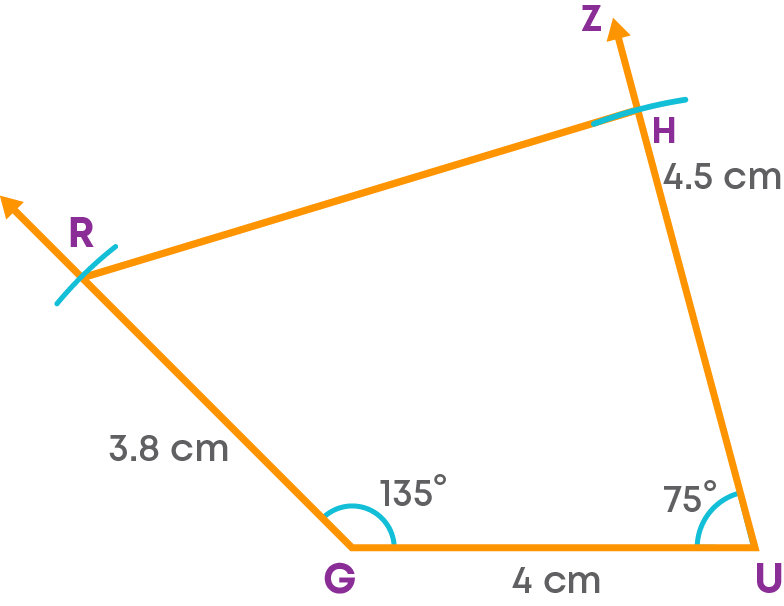
RGUH is the required quadrilateral.
Constructing Parallelograms
Let us understand the method of constructing a parallelogram when the two adjacent sides and a diagonal are given.
Construct the parallelogram ABEF with AB = 3.5 cm, BE = 3 cm, and the diagonal BF = 4 cm.
Step 1: Draw the side AB = 3.5 cm as the base. Construct the triangle ABF with AF = 3 cm and BF = 4 cm.

Step 2: With the diagonal BF as the base, construct the triangle BEF with BE = 3 cm and EF = 3.5 cm.
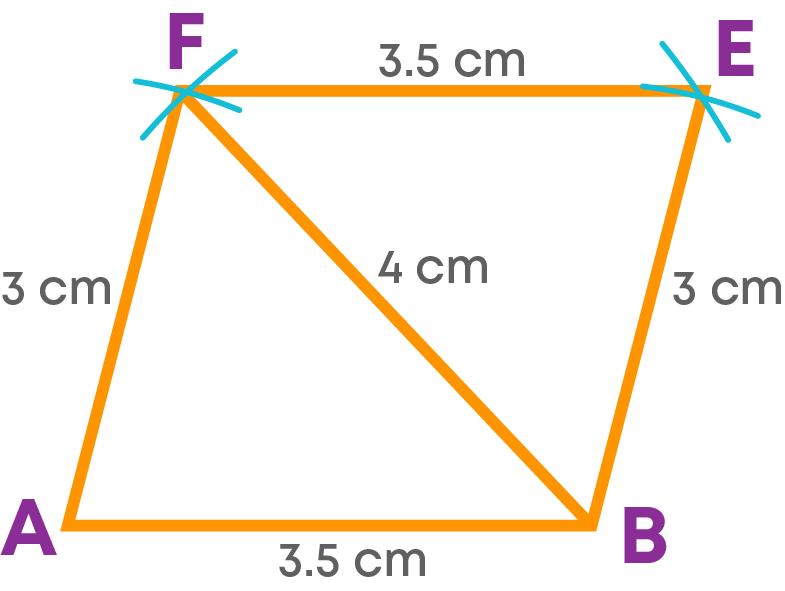
ABEF is the required parallelogram. Let us see the steps of construction.

Using the properties of the sides and angles of a parallelogram, let us see how to construct a parallelogram when the length of the adjacent sides and the angle between them are given.
Construct a parallelogram DFGH with FG = 3 cm, GH = 3.5 cm and ∠GFD = 60⁰.
Let us find the measures of the remaining two sides and the angle adjacent to the given angle.
FG = DH = 3 cm
GH = DF = 3.5 cm
∠HGF = 180⁰ - 60⁰ = 120⁰
Using the measurements, we must construct the parallelogram.
- We must first draw the rough sketch of the required parallelogram.
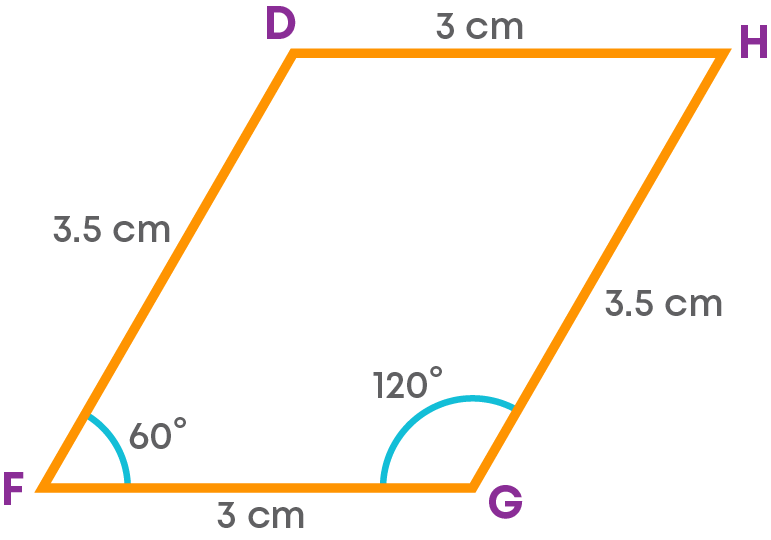
From the rough figure, we see that we have the measures of the three sides and the two angles included between them.
Hence, we will use the method of constructing a quadrilateral when the three sides and two angles between them are given.
Steps of construction:
Step 1: Draw the side FG = 3 cm.

Step 2: Construct an angle FGX = 120° at G.
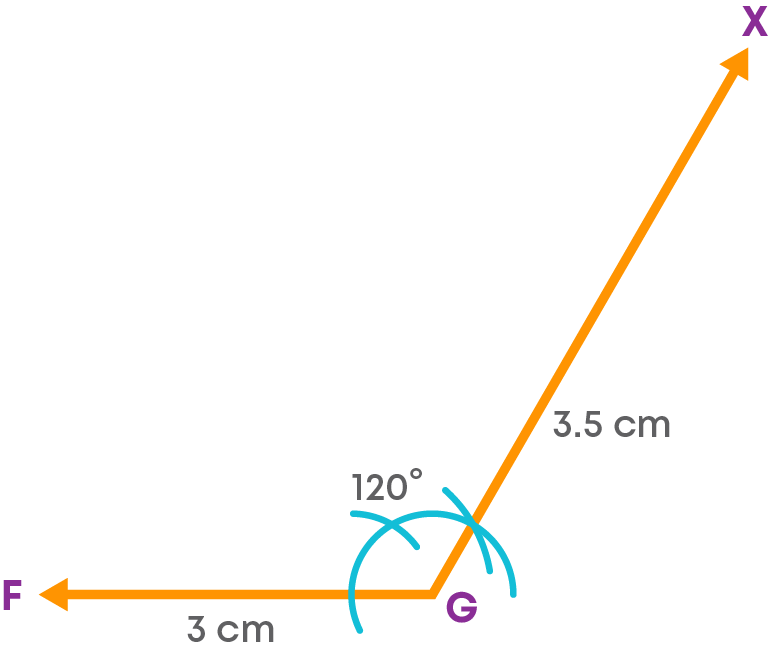
Step 3: With G as the centre and radius 3.5 cm, cut off an arc on GX at H.
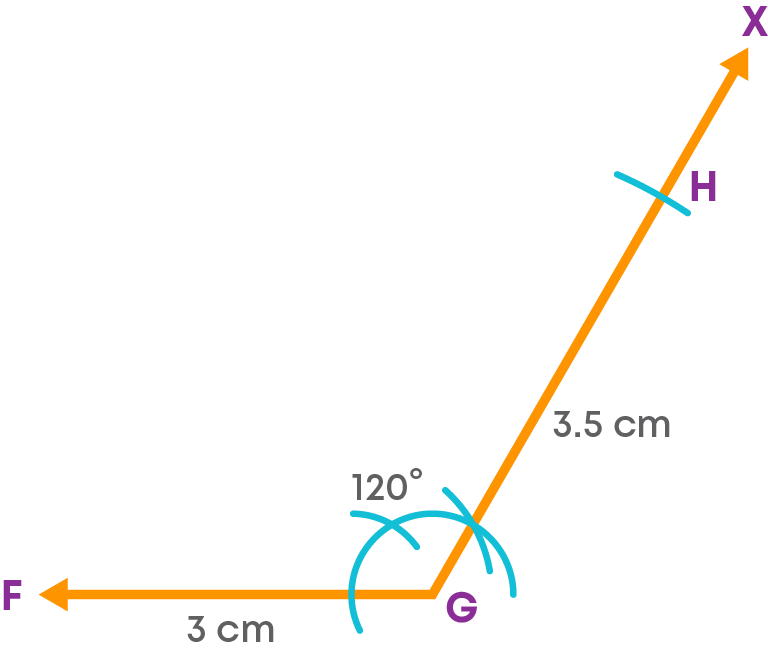
Step 4: Construct an angle at F.
Construct an angle ∠GFY = 60⁰ at F.
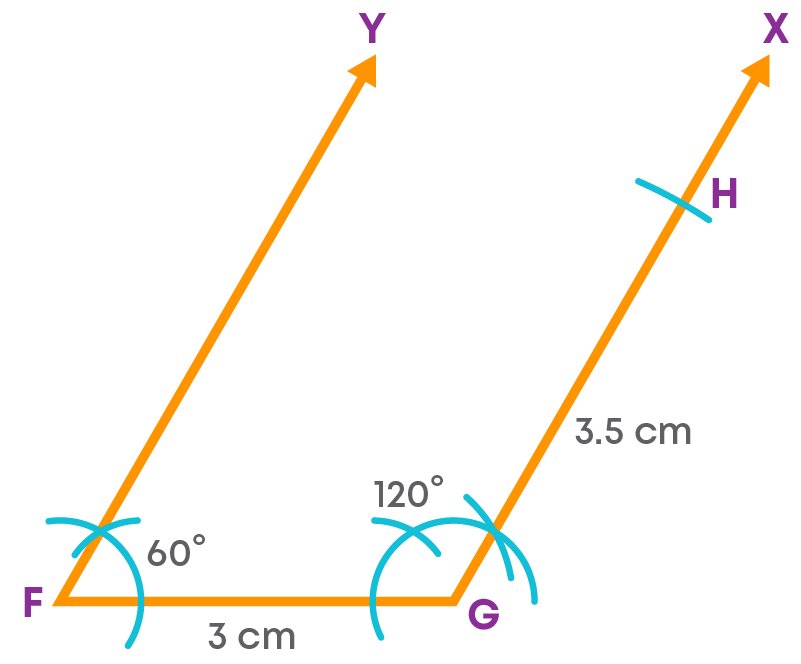
Step 5: With F as the centre and radius 3.5 cm, draw an arc on FY at D.
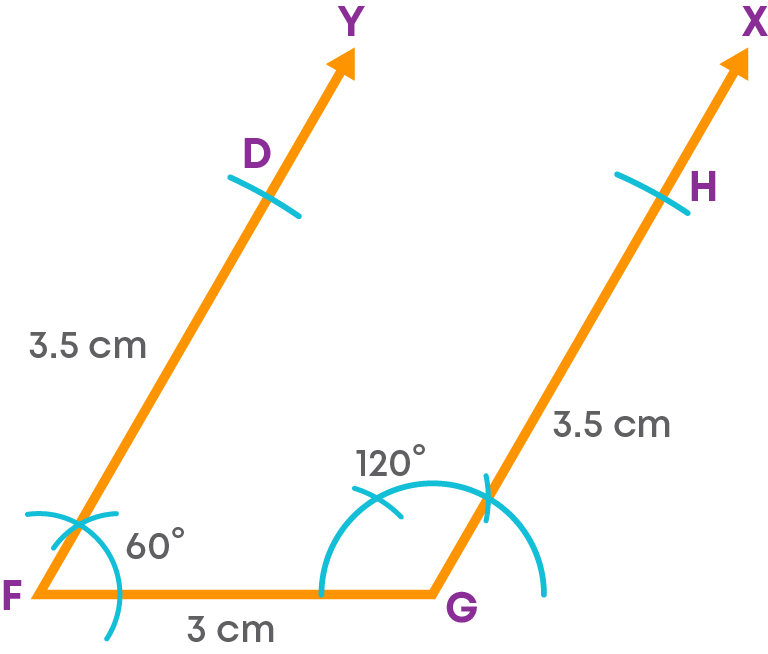
Step 6: Join D and H.
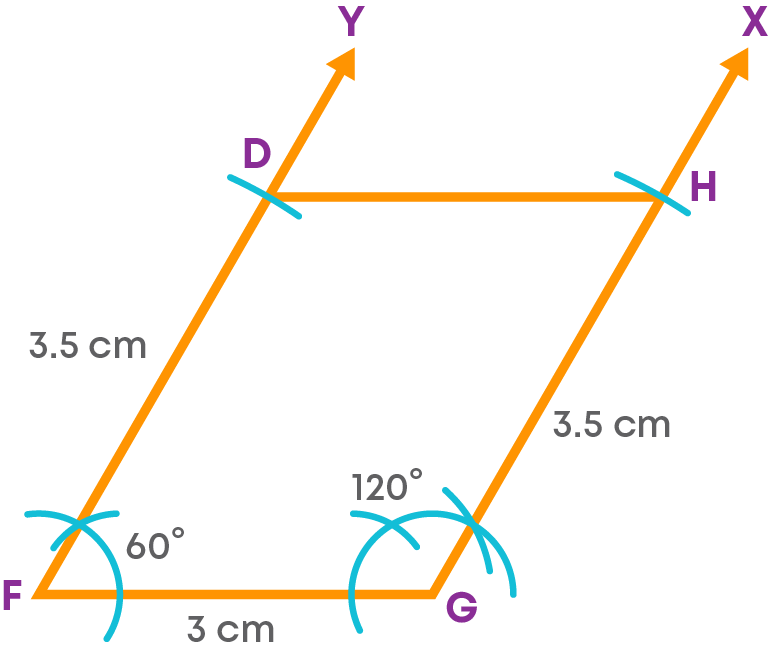
DFGH is the required parallelogram.
Let us see the steps of construction.

Using the properties of the diagonals, let us see how to construct a parallelogram when the lengths of the two diagonals and the measure of the angle between them are given.
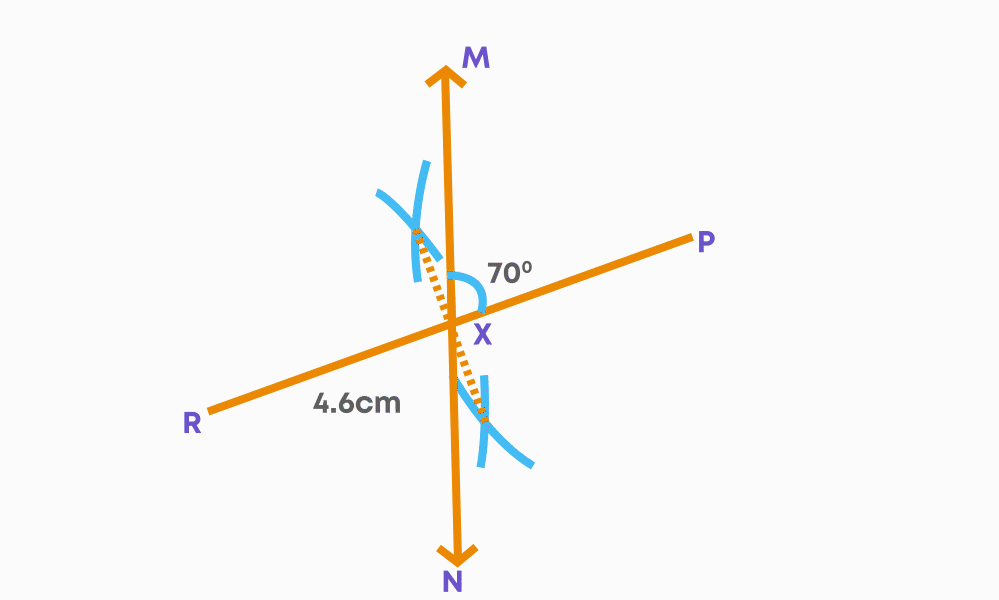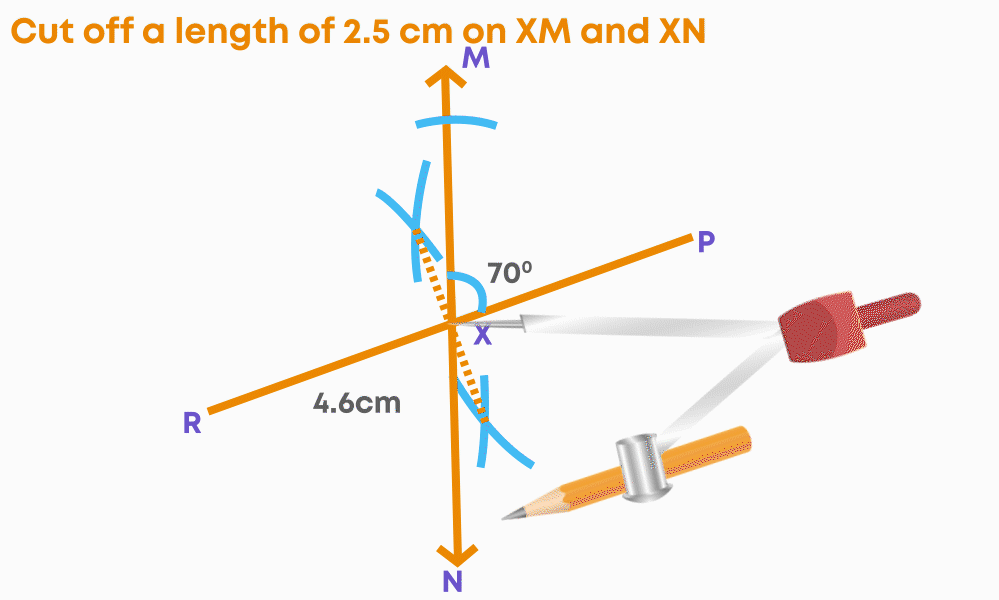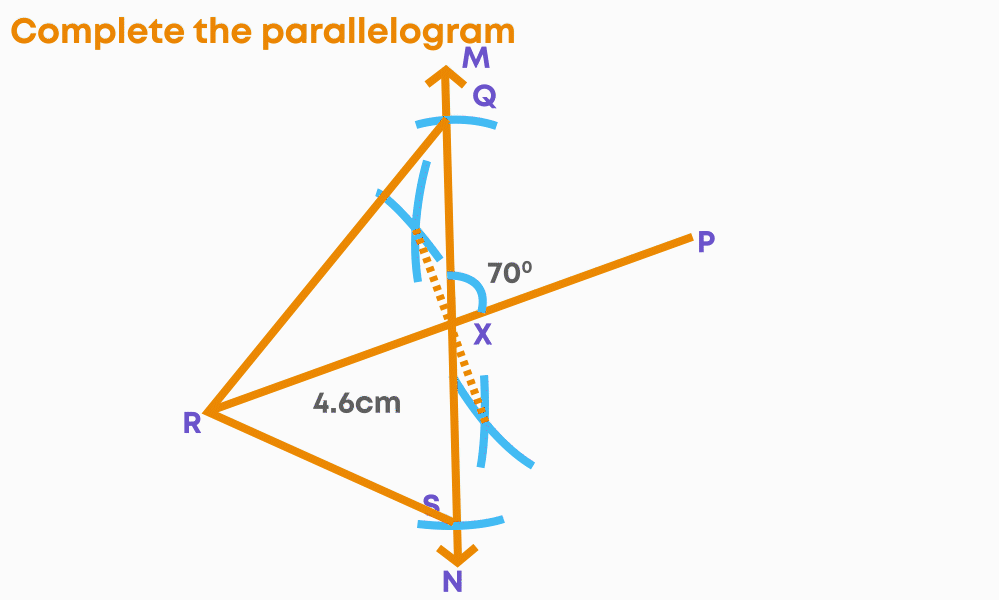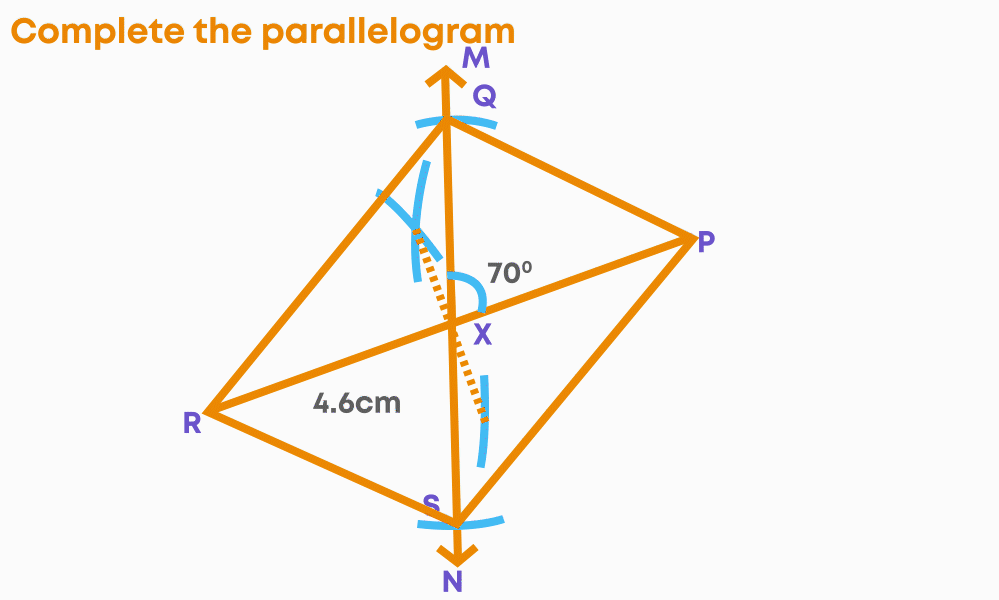
Construct a parallelogram PQRS with QS = 5 cm and PR = 4.6 cm. The angle between the diagonals is 70⁰.
Mark the point of intersection of the diagonals as X. Construct the angle ∠PXS = 70⁰.
The rough sketch of the required parallelogram is:

Steps of construction:
- Step 1: Draw the diagonal PR = 4.6 cm.

- Step 2: Using a compass and ruler, bisect PR. Mark the point of bisection as X.
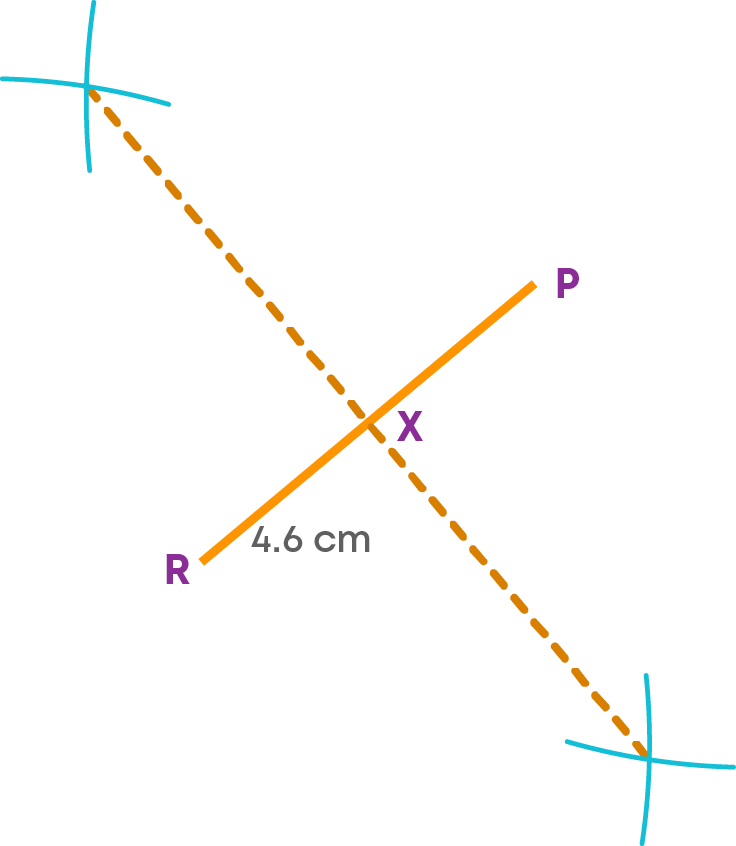
- Step 3: Draw an angle ∠MXP = 70⁰.
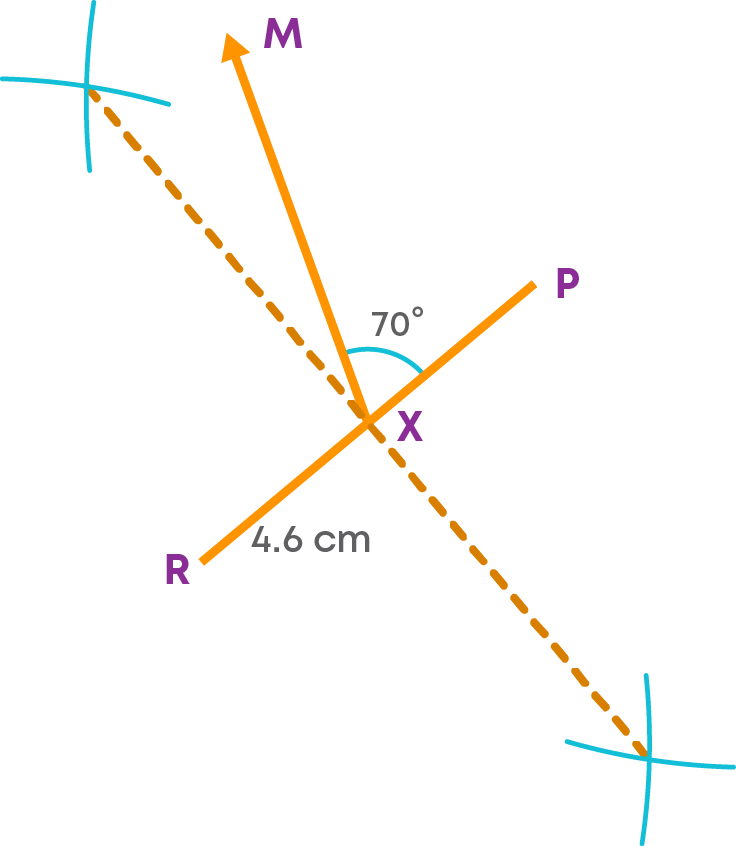
- Step 4: Extend MX to XN on the other side of PR.
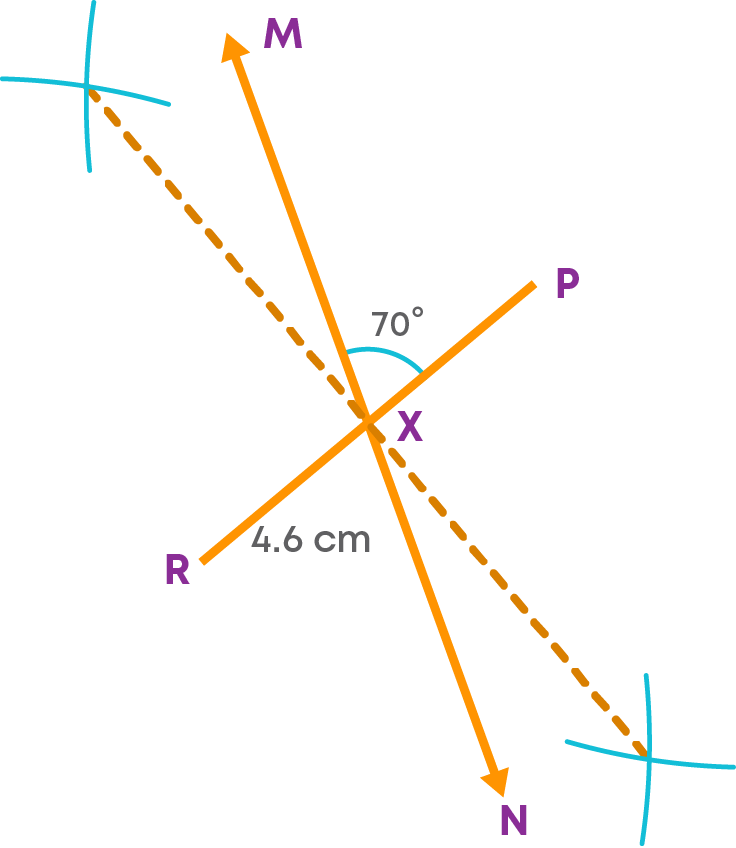
- Step 5: We know that QS = 5 cm.
Since, it is bisected at X, we have QX = XS = 2.5 cm. Cut off a length of 2.5 cm on either side of X on MN.
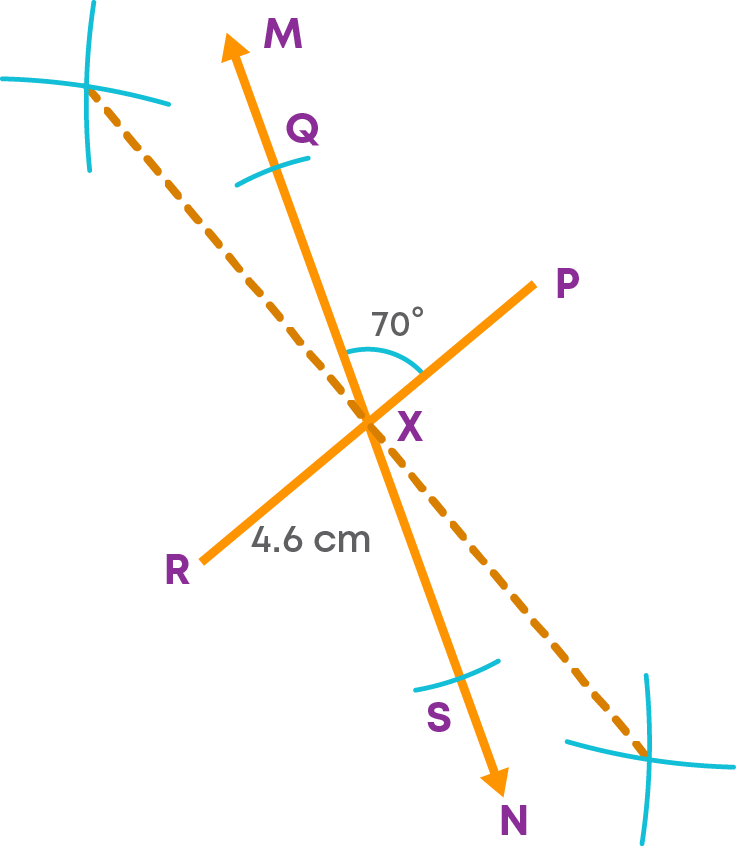
- Step 6: Join PQ, QR, RS and PS.
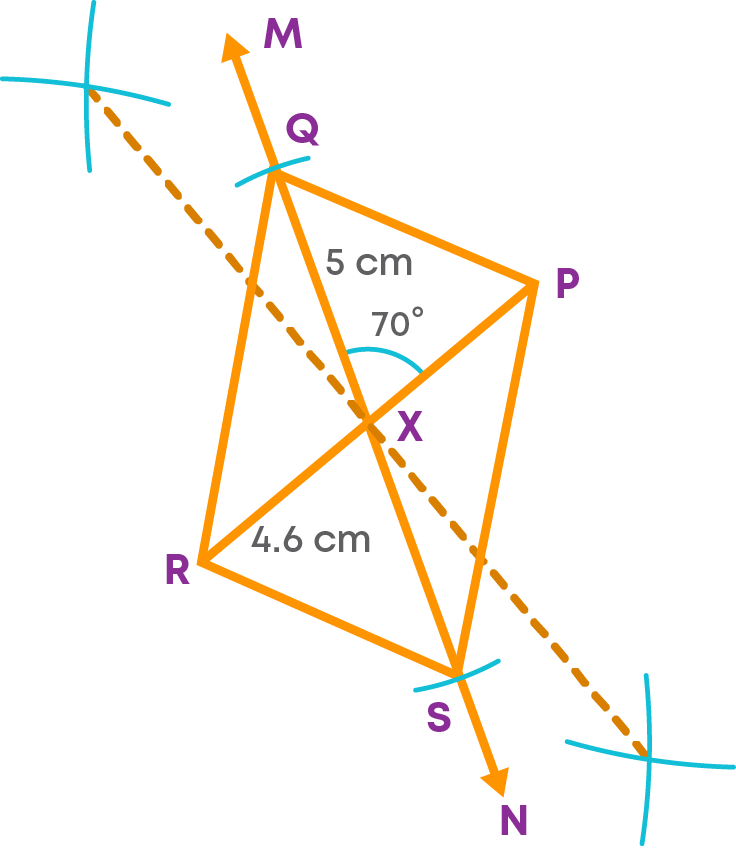
PQRS is the required parallelogram. Let us see the steps of constructing the parallelogram.
(1) Construct the diagonals with the given angle between them.

(2) Complete the parallelogram
Observe the parallelogram given below:
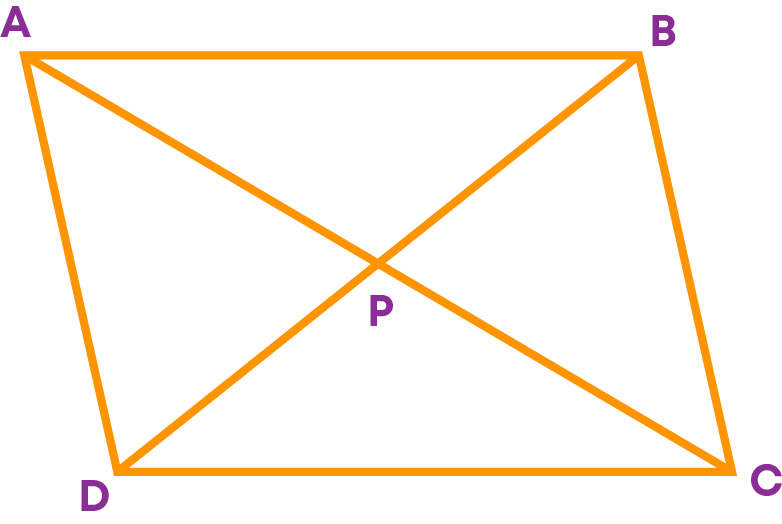
In the parallelogram ABCD, we can observe that:
- The diagonals form triangles.
- Four bigger triangles are formed. Namely, ∆ADC, ∆BDC, ∆ABD and ∆ABC.
- Four smaller triangles are formed. Namely, ∆DPC, ∆BPC, ∆APB and ∆APD.
Now, in a parallelogram DEFG, the length of the side EF = 3.5 cm, the length of the diagonal DF = 4.8 cm and diagonal EG = 6.2 cm.
Let us draw a sketch of the parallelogram.
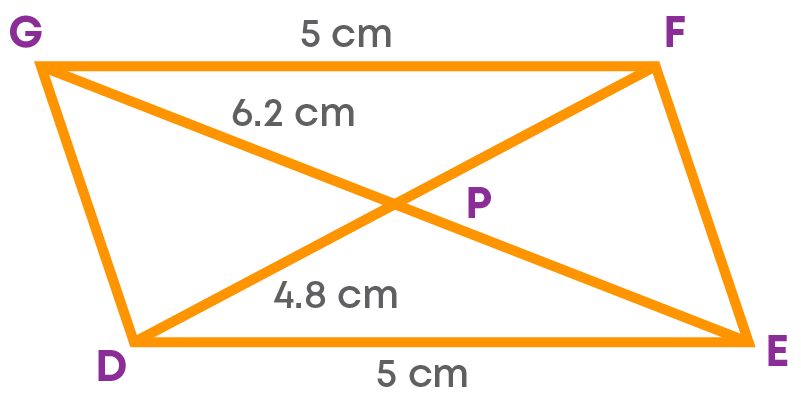
Applying the properties of a parallelogram, we get
DP = 2.4 cm
EP = 3.1 cm
Now, we have the measures of the sides of the triangle DPE. Hence, we can start by constructing the small triangle formed by the given side and half the lengths of the diagonals. Then, we complete the parallelogram by extending the diagonals.
When the side and the lengths of the diagonals are given, we can begin by constructing the triangle formed by the side and half the lengths of the diagonals.
Construct a parallelogram ABCD with AB = 4.7 cm, AC = 4.4 cm, and BD = 6.4 cm.
First, let us draw a rough sketch of the parallelogram.
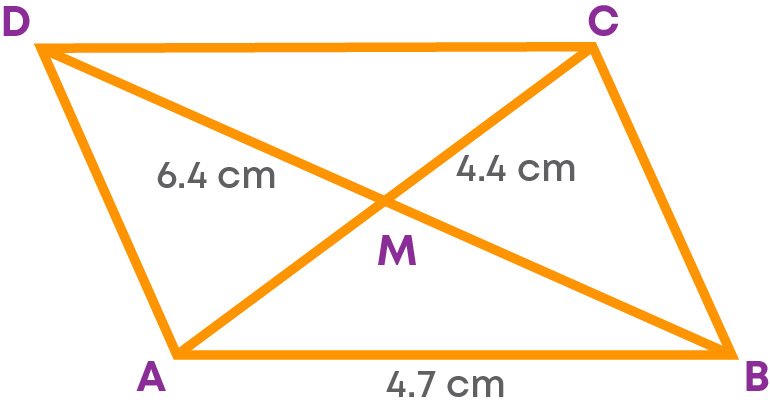
Also, let us draw the sketch of the triangle AMB.
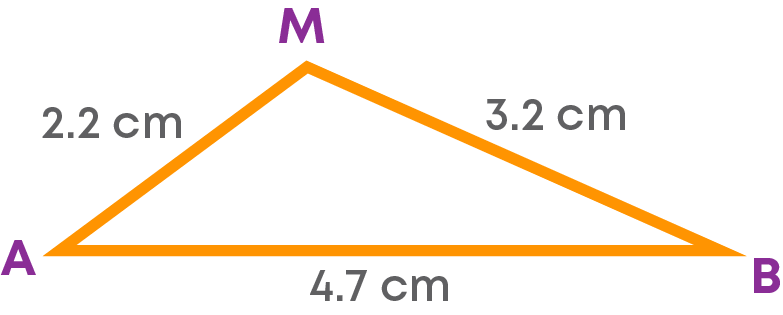
Now, let us construct the parallelogram ABCD.
Step 1: Draw the given side AB = 4.7 cm.

Step 2: Construct the triangle AMB formed by the side AB and half of each diagonal.
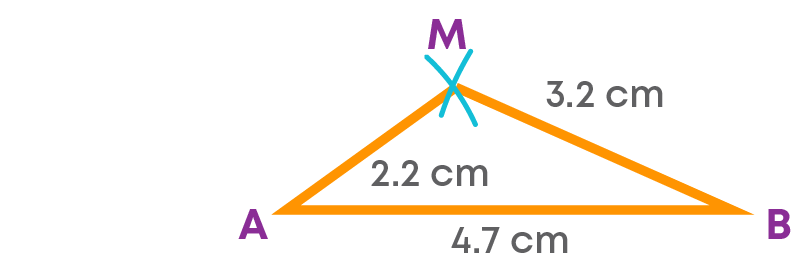
Step 3: Extend AM to X and BM to Y.
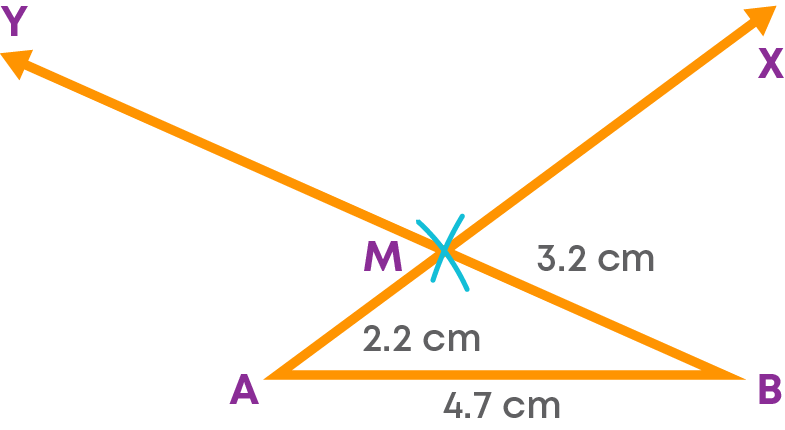
Step 4: With M as the centre, take a radius of 3.2 cm and draw an arc on MY at D. With M as the centre and the radius as 2.2 cm, draw an arc on MX at C.
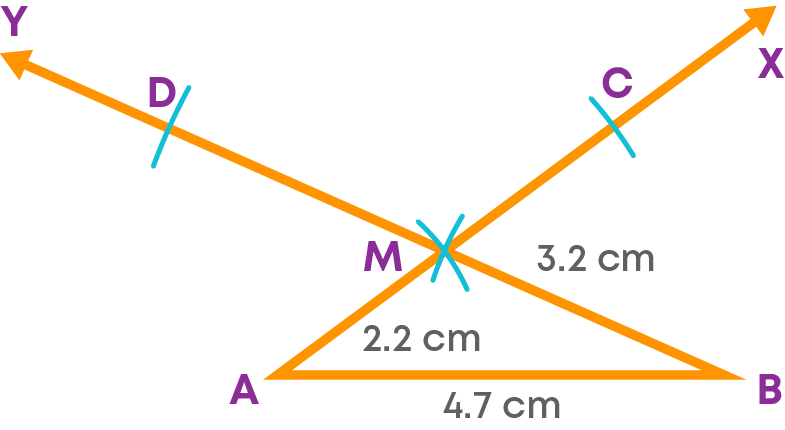
Step 5: Join BC, CD and AD.
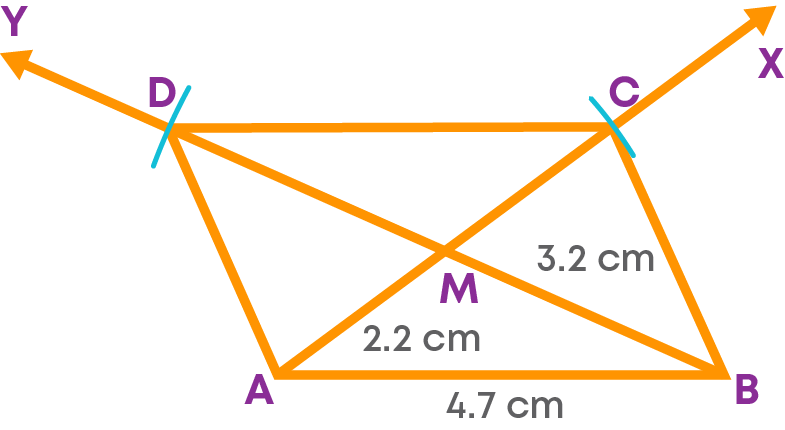
ABCD is the required parallelogram. Let us see the steps of construction.

To construct any quadrilateral, we need to know the measures of minimum 5 elements of the quadrilateral. We know that a square is a special quadrilateral. If we know the length of one of the sides, we can infer the lengths of the other three sides. Also, in a square, all angles are 90°. This gives us the minimum information required to construct the desired square.
How do we construct a square when we are given the length of a side? Let us understand with an example:
Construct a square JKLM with each side of length 3 cm.
First, we must draw a rough sketch of the required square.
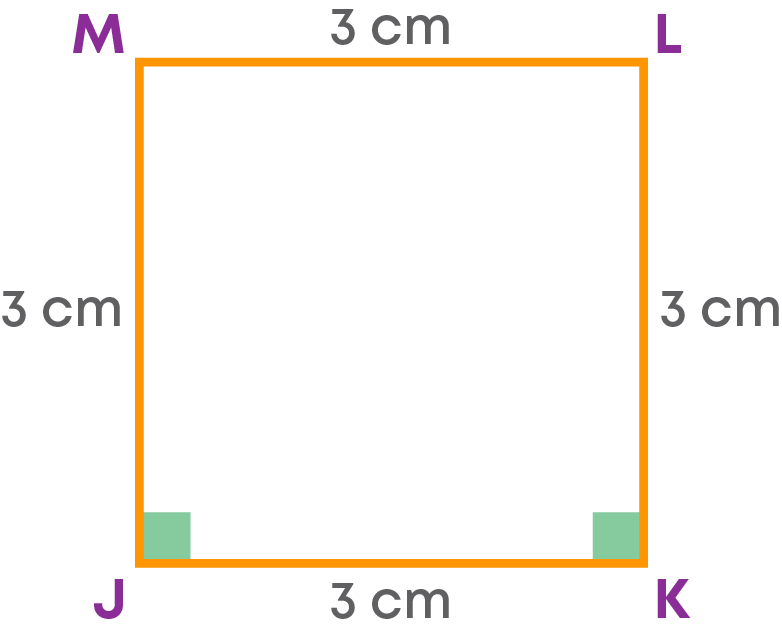
Now, let us construct the square.
Step 1: Draw the side JK = 3 cm.

Step 2: Construct a 90° angle at J and K.

Step 3: On the arms of these angles, cut off a length equal to 3 cm each. Mark the points made by the arc as M and L.
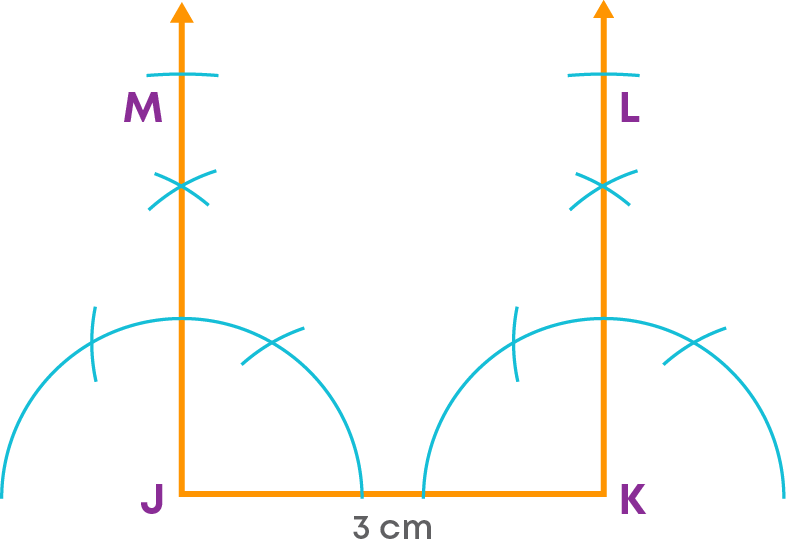
Step 4: Join the vertices M and L.
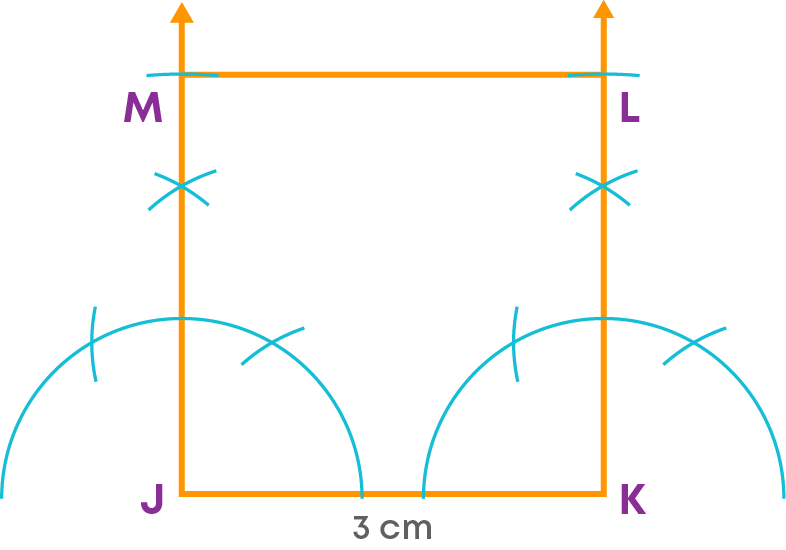
JKLM is the required square. Let us see the steps of construction.

To construct a square when the length of a diagonal is given:
- We need to understand that the length of the other diagonal is the same as the given length.
- The angle between the diagonals is 90⁰.
Construct a square RSTU with a diagonal of length 3.6 cm.
Let us construct a square RSTU.
- Step 1: Draw the diagonal RT = 3.6 cm. Construct the perpendicular bisector of the diagonal RT. Mark the point of intersection of the diagonal and the bisector as ‘X’.
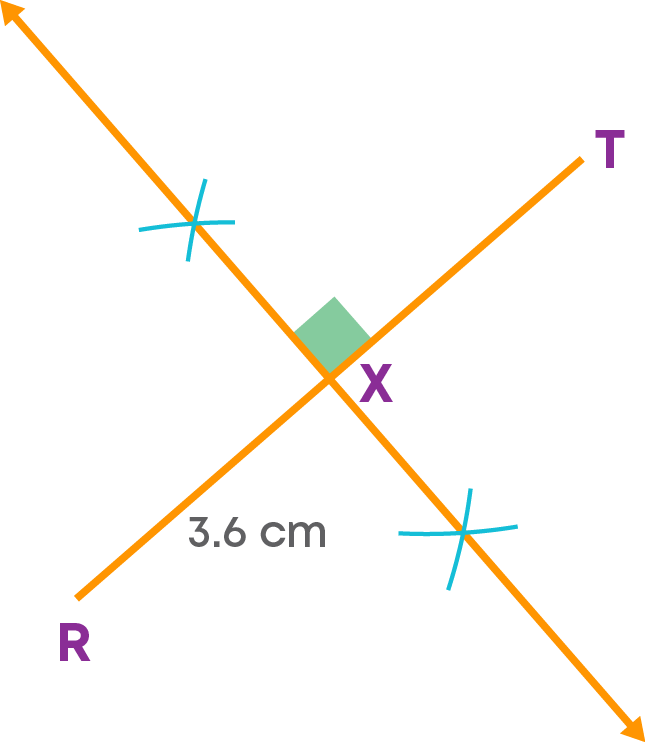
- Step 2: With X as the centre and a radius of 1.8 cm, cut off the length on either side of the bisector at S and U.
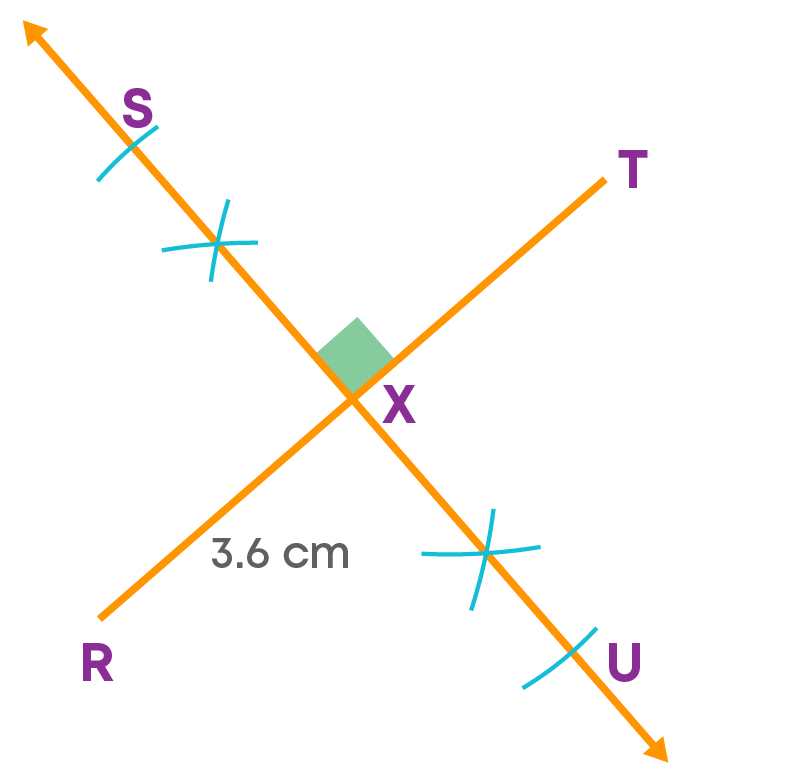
- Step 3: Join RS, ST, TU and RU.
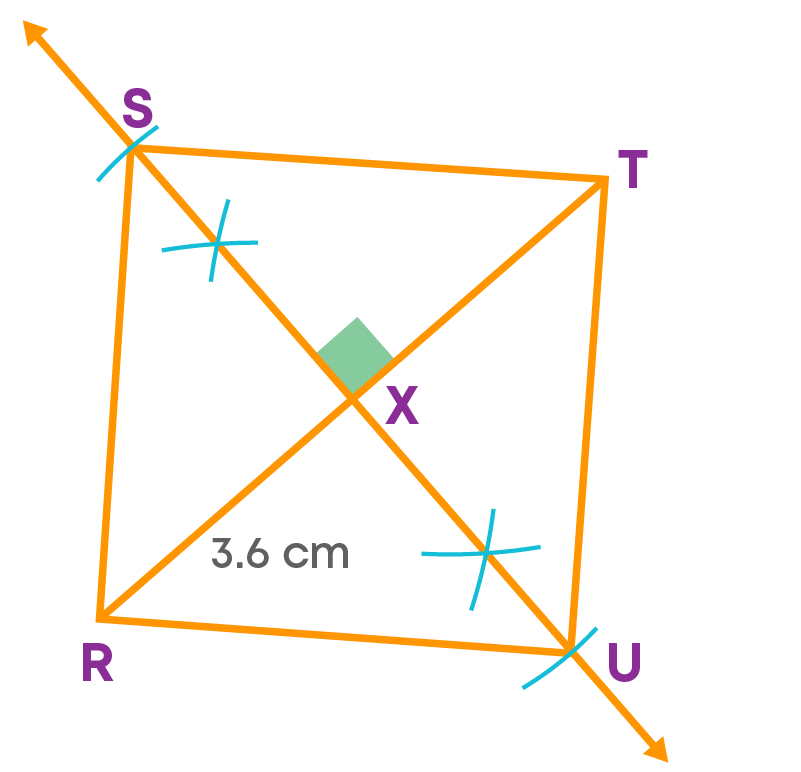
RSTU is the required square. Let us see the steps of construction.

When the lengths of the adjacent sides of a rectangle are given, the strategy to construct the rectangle is:
- With one of the sides as the base, we can construct right angles at each end of the base.
- On the arms of these angles, we need to cut off a length equal to the adjacent side given.
To construct a rectangle ASDF with AS = 4 cm and AF = 3 cm, we follow these steps:
Step 1: Draw side AS = 4 cm.

Step 2: Construct 90° angle at A and S.

Step 3: On the arms of the 90° angles, cut off a length of 3 cm each at D and F.

Step 4: Join D and E.
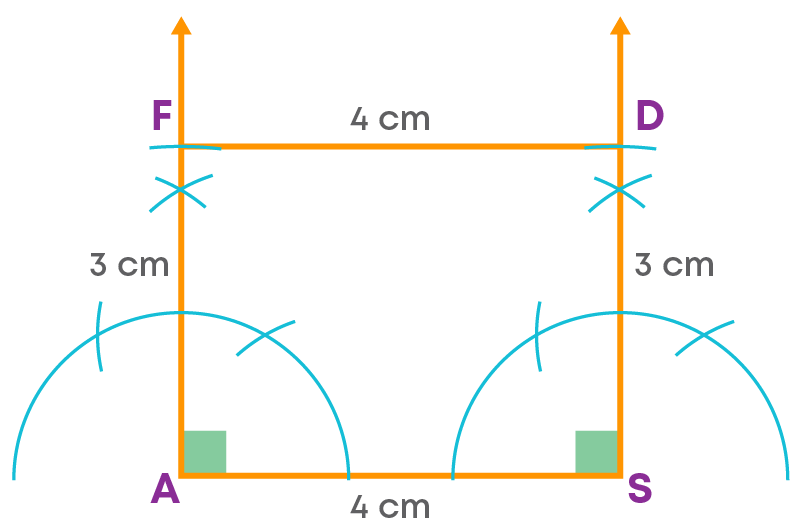
ASDF is the required rectangle. Let us see the steps of construction.

When a side and an angle of a rhombus are given, we can find the lengths of the remaining sides and angles. This gives us the minimum information required to construct it.
Construct a rhombus JKLM of side 2.8 cm and ∠KLM = 50⁰.
First, find the measures of the other sides and angles:
Each side = 2.8 cm
JK = KL = LM = JM = 2.8 cm
∠KLM = ∠MJK = 50⁰
∠JML = ∠JKL = 180 – 50 = 130⁰
Rough sketch of the required rhombus:
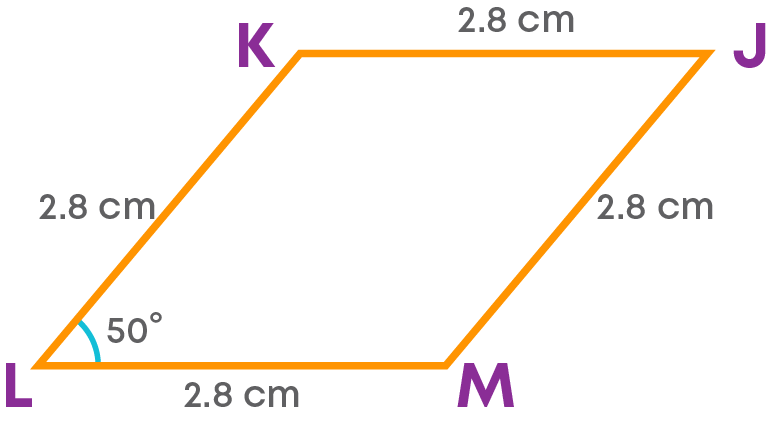
Constructing the rhombus:
Step 1: Draw the side LM as the base.

Step 2: Draw an angle of 50⁰ at L and an angle of 130⁰ at M.
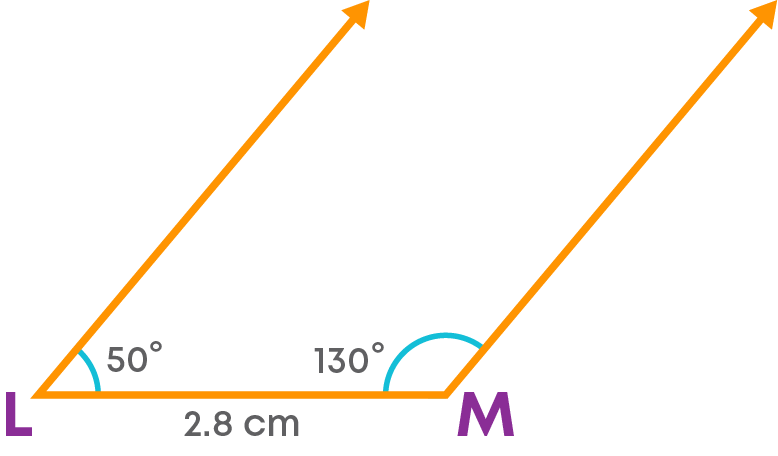
Step 3: With L as the centre and a radius of 2.8 cm, draw an arc on the arm of the angle at K
Similarly, with M as the centre, draw an arc on the arm of the angle drawn here at J.
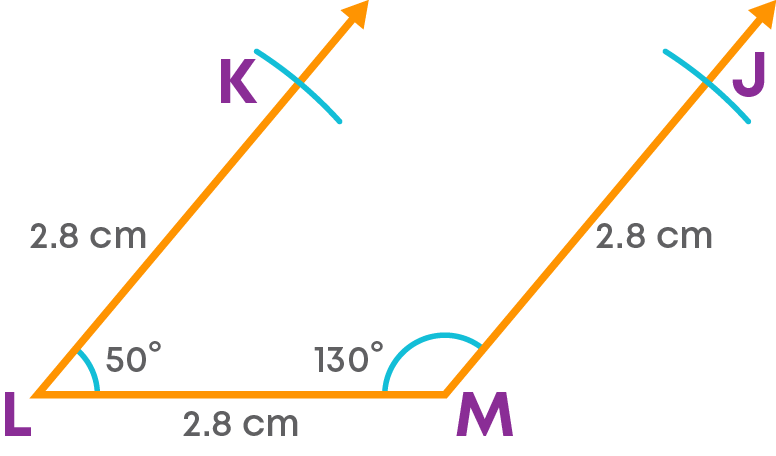
Step 4: Join KJ.
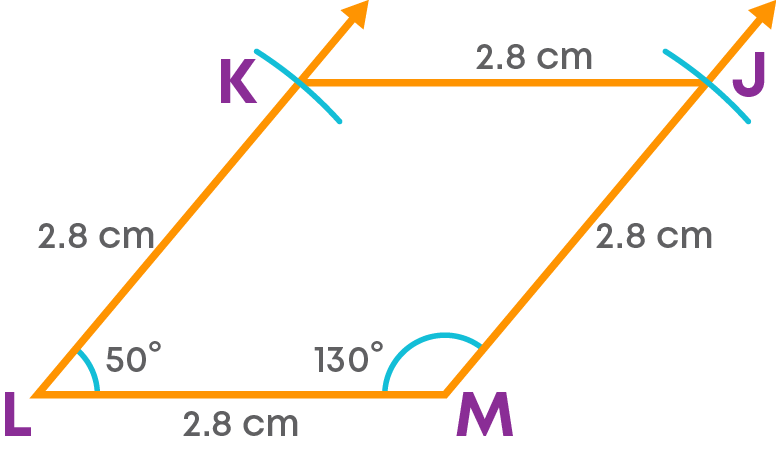
JKLM is the required rhombus. Let us see the construction.

Can you construct a rhombus when the lengths of diagonals are given? Let us learn how with an example.
Construct a rhombus WERT with diagonal WR = 5 cm and ET = 4 cm.
Let us draw the rough sketch of the required rhombus.
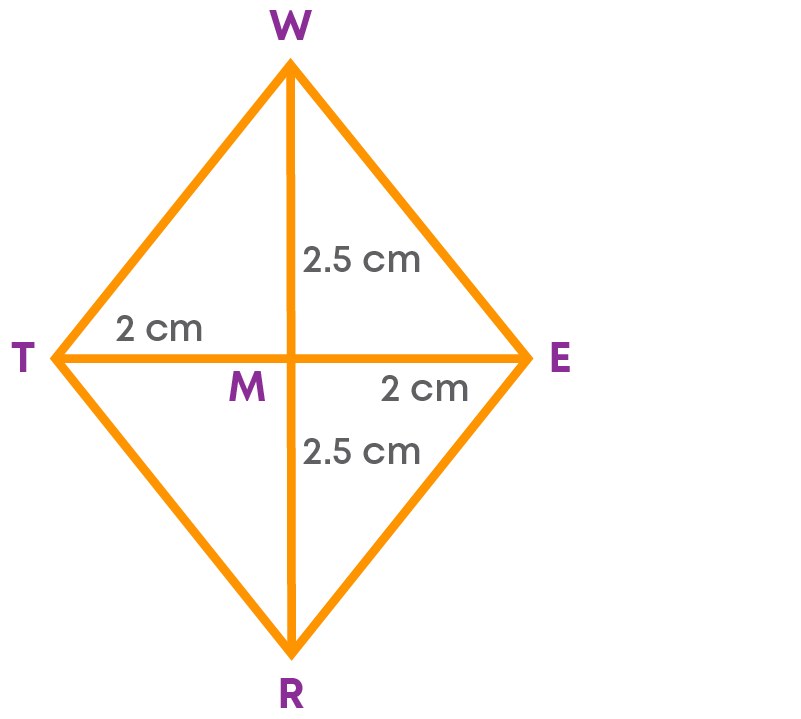
Now, let us construct the rhombus.
Step 1: Draw the diagonal TE = 4 cm.

Step 2: Construct the perpendicular bisector of the diagonal. Mark the point of intersection as ‘M’.
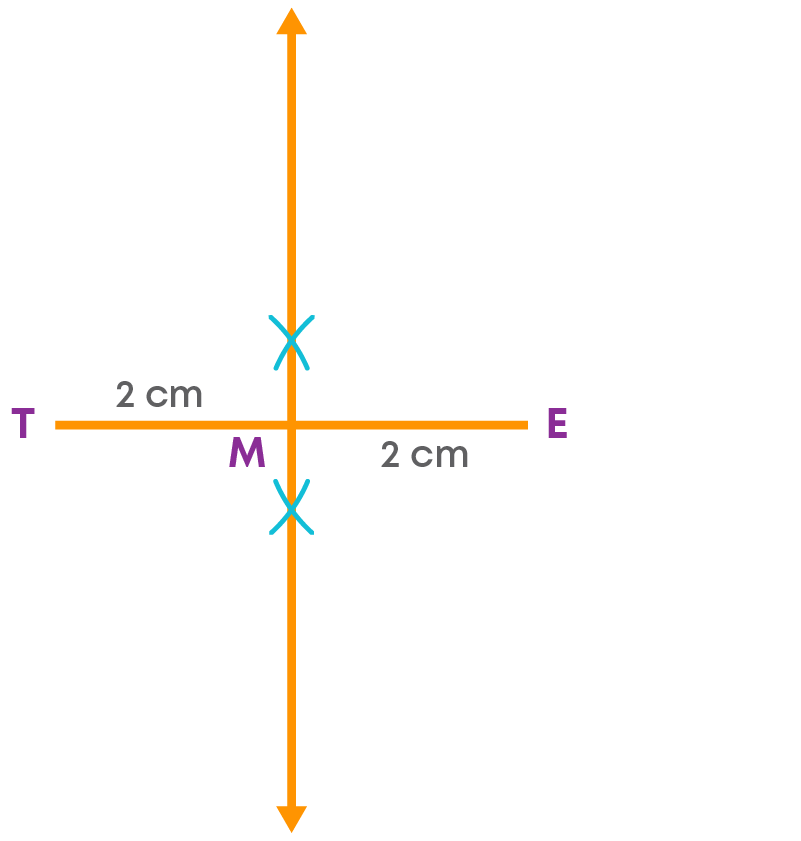
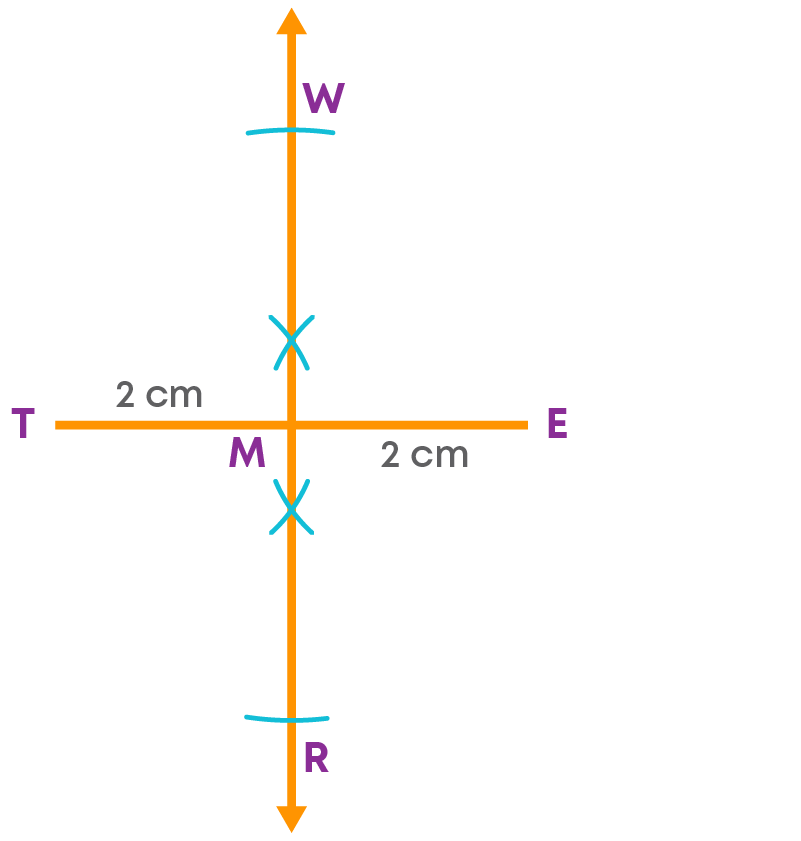
Step 3: Now, the other diagonal is 5 cm.
This means, on either side of the bisector, we must cut off a length which is half of 5 cm. Half of 5 cm is 2.5 cm. Cut off a length of 2.5 cm on both sides of the bisector. With ‘M’ as centre and a radius of 2.5 cm, cut an arc on the perpendicular bisector at W. With the same radius and centre, cut off another arc on the other side at R. These will be the other two vertices of the rhombus.
Step 4: Join the vertices of the rhombus.
Join WT, TE, ER and TR.
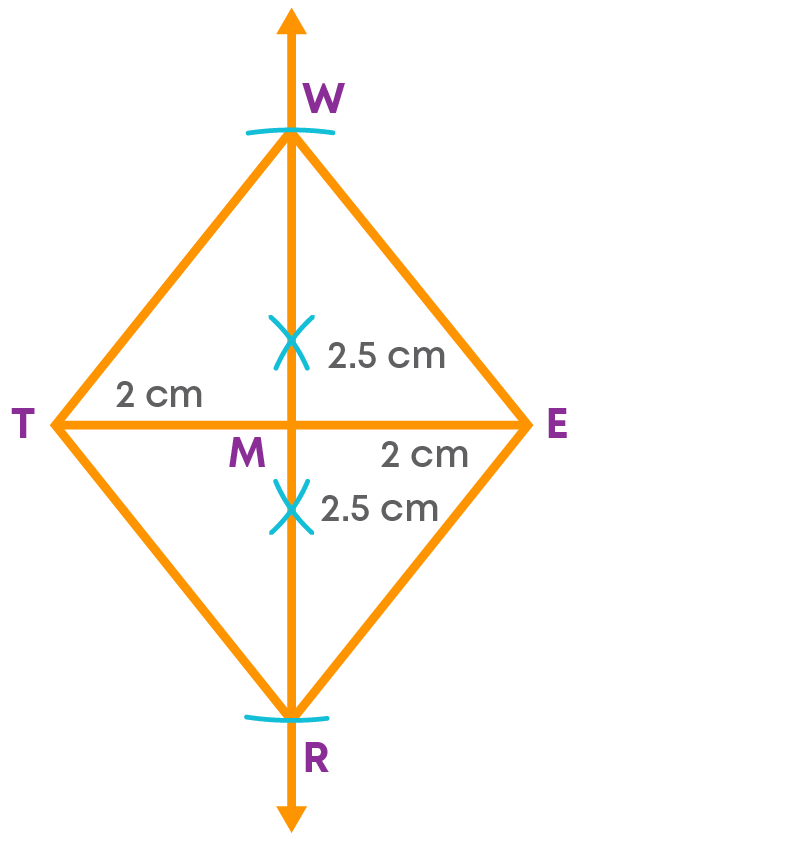
WERT is the required rhombus.
Common Errors
The following are topics in which students make common mistakes when dealing with practical geometry:
- 1. Constructing a quadrilateral
- 2. Draw the rough figure of the required quadrilateral

Draw The Rough Figure Of The Required Quadrilateral
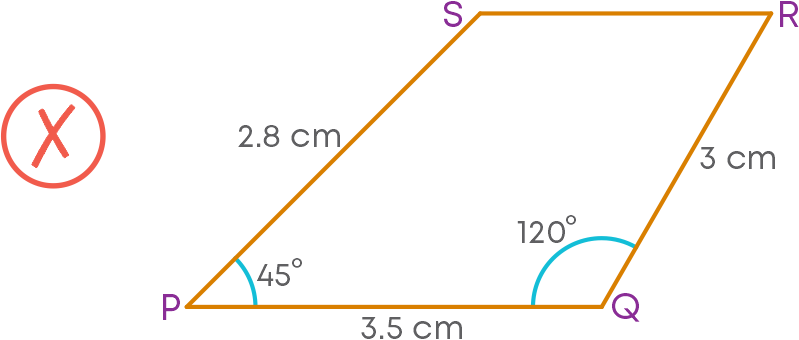
Before doing the actual construction with a compass and ruler, draw a rough figure of the required quadrilateral and mark the respective measures of sides / angles / diagonals. Example:
Construct a quadrilateral PQRS with PQ = 3 cm, QR = 2.8 cm, PS = 3.5 cm, ∠SPQ = 45⁰ and ∠PQR = 120⁰.
First, draw a rough figure of the required quadrilateral. The rough figure will help to understand how to construct the quadrilateral. Remember to mark the corresponding measures given correctly in the rough figure.
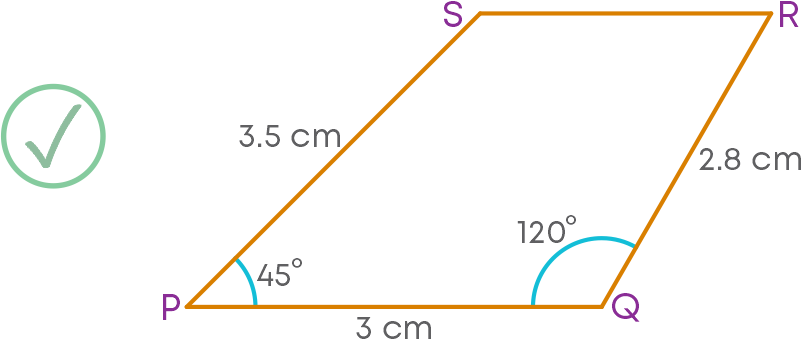
Constructing A Parallelogram
While constructing a parallelogram, you will find that the measure of adjacent sides is given and the angle between them is given. Do not mistake it for insufficient information. Remember to apply the properties of a parallelogram to find the other required measures.
- Adjacent sides are given, their corresponding opposite sides will be equal.
- Angle between the two sides is given.
This means the opposite angle is of the same measure, and its adjacent angle will be 180⁰ - the given angle.
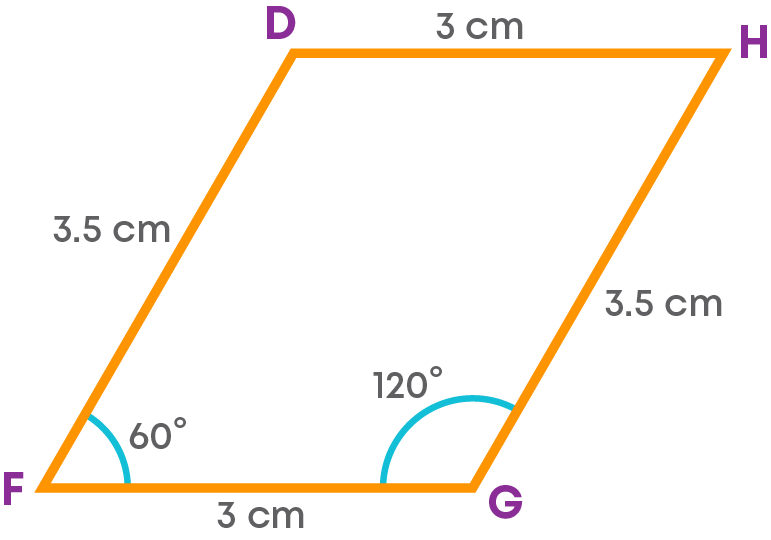
Example:
To construct a parallelogram DFGH with FG = 3 cm, GH = 3.5 cm and ∠FGH = 120⁰.
Here, the measures of the adjacent sides are given. The sides opposite to these sides will also be of the same measure. That is, FG = DH = 3 cm, GH = DF = 3.5 cm. Now, the ∠FGH = 120⁰.
The angle opposite to this angle will be equal, i.e., ∠FGH = ∠FDH = 120⁰.
Also, the sum of the adjacent angles will be 180⁰.
So, ∠FGH + ∠DFH = 180⁰.
∠DFH = 60⁰
Now, we have the measures of 4 sides and two angles. With this we can construct the parallelogram.
Conclusion
Now that you have learnt about construction of quadrilaterals and parallelograms, can you solve the following riddle?
Reeta constructed the figure given below:
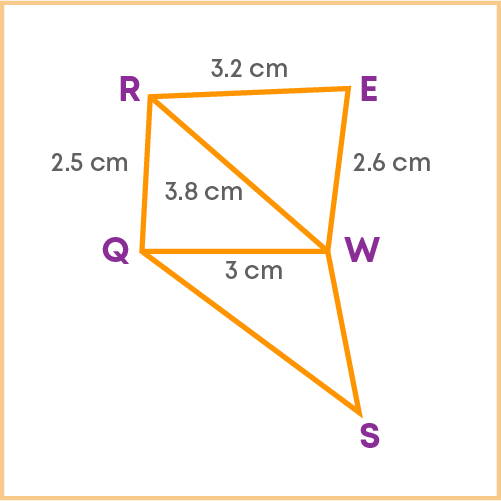
In this,
QWER is a quadrilateral whose measures are given as: QW = 3 cm, QR = 2.5 cm, RE = 3.2 cm, WE = 2.6 cm, and RW = 3.8 cm.
QS is parallel to RW and QR is parallel to WS.
Complete the following steps of construction
Step 1: Construct _____ with QW = 3 cm as the base, QR = 2.5 cm and RW = 3.8 cm
Step 2: Construct _____ with RW as the base and sides RE = 3.2 cm and EW = 2.6 cm
Step 3: Construct _____ with QW as base and sides _____ .




















































