Introduction
In our day-to-day life, we frequently encounter situations where the variation in values of a certain quantity is influenced by the variation in values of the other quantity.
For example, the siren of an approaching fire engine or an ambulance becomes louder as the vehicle nears you and quieter as it gets farther away from you.
You noticed that the lesser the distance between you and the vehicle, the louder the siren and the more the distance, the quieter the siren becomes.
Watch the video below to know more.
If the values of two quantities depend on each other in such a way that a change in one causes a corresponding change in the other, then the two quantities are said to be in variation.
There are two types of variations:
- Direct proportion
- Indirect or inverse proportion

Sometimes, we observe that the variation in the value of one quantity is similar to the variation in the value of the other quantity, that is when the value of one quantity increases then the value of the other quantity also increases in the same proportion and vice versa.
In such situations, two quantities are termed to exist in direct proportion.
In an inverse variation, it's exactly the opposite: as one number increases, the other decreases. This is also called the inverse proportion.
Concepts
The chapter ‘Direct and Inverse Proportion’ covers the following concepts:
Direct Proportion
You know the meaning of ratio. If two ratios are equal, we can say that the quantities in the ratios are in proportion.
In many situations in our day-to-day life, we can see that the variation in one quantity brings in a variation in the other quantity. For example:
If the cost of 1 kg of rice is ₹40, then what would be the cost of 3 kg of rice?
If one kg rice costs ₹40, then cost of 3 kg of rice = 3 x ₹40 = ₹120. Similarly, we can find the cost of 5 kg or 6 kg of rice.
Observe the following table:
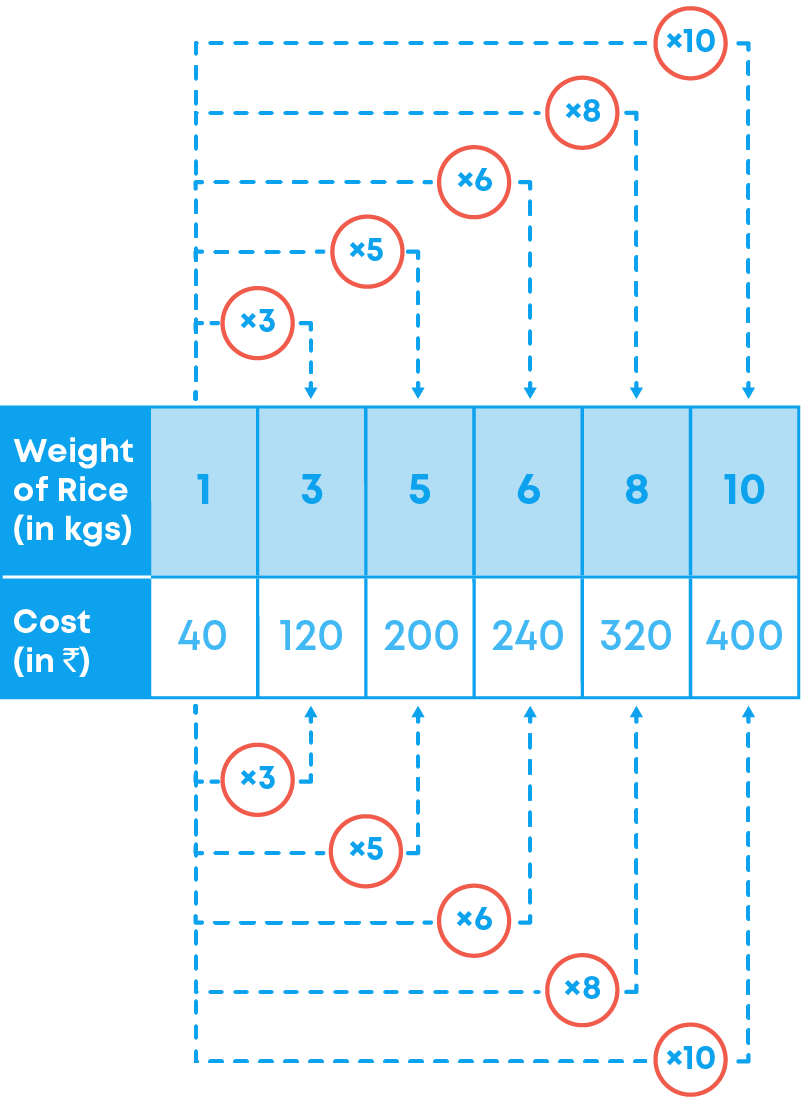
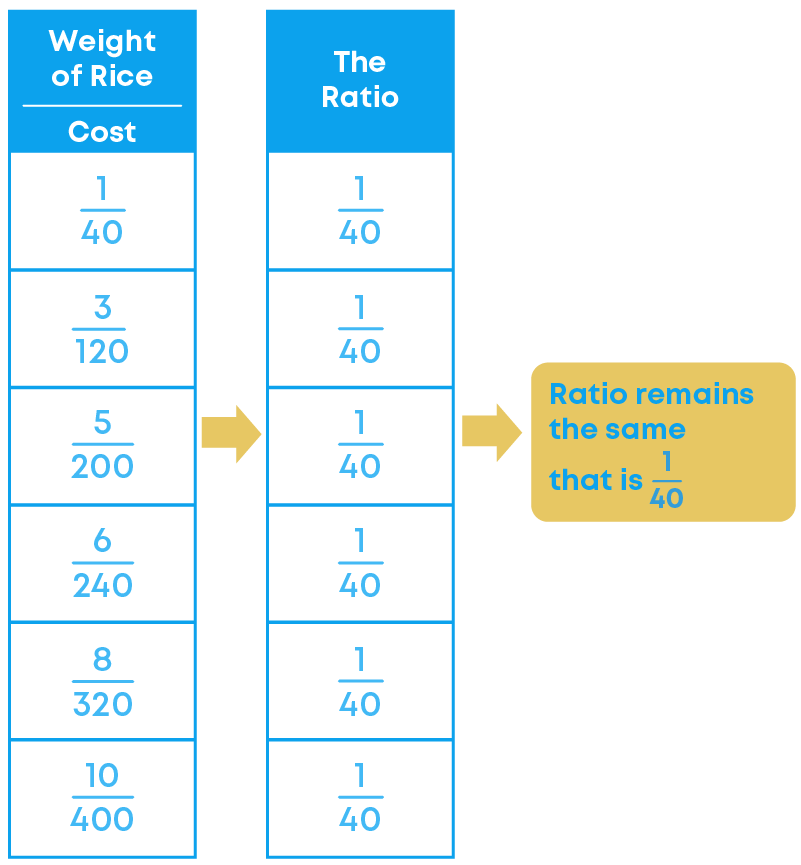
Observe that as the weight of the rice increases, the cost also increases in such a manner that their ratio remains constant.
Two quantities ‘x’ and ‘y’ are said to be in direct proportion if:
- Increase in ‘x’ increases the value of ‘y’
- Decrease in ‘x’ decreases the value of ‘y’
But the ratio of their respective values must be the same.
‘x’ and ‘y’ will be in direct proportion if x y = k (k is a constant) or x = ky
When ‘x’ and ‘y’ are in direct proportion, we can write:
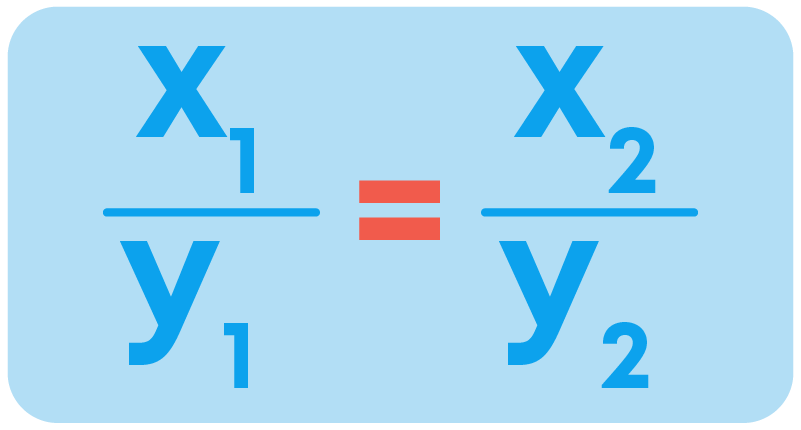
(y1, y2 and x1, x2 are the corresponding values of ‘y’ and ‘x,’ respectively)
The direct proportion is also known as direct variation.
When ‘x’ and ‘y’ are in direct proportion (or vary directly), they are also written as:

Suppose the minute hand of a clock is at 12 initially and it starts moving. Record the angle through which the minute hand has turned from its original position and the time that has passed, in the following table:
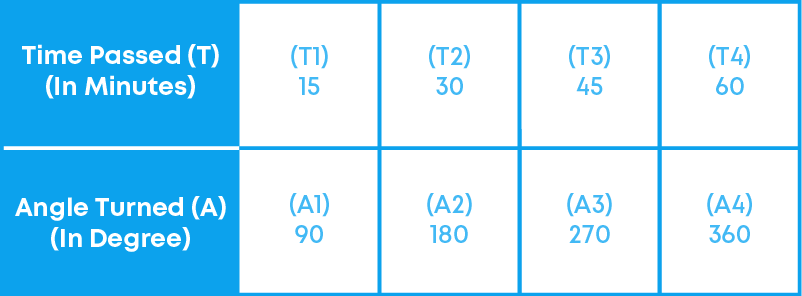
Now, let us find the ratio of the time passed to the angle, in each case:
T1 A1 = 15 90 = 1 6
T2 A2 = 30 180 = 1 6
T3 A3 = 45 270 = 1 6
T4 A4 = 60 360 = 1 6
What do you observe about T and A? Do they increase together? Is T A the same every time?
Yes! We see that the ratio T A remains the same which is 1 6
We know that ‘x’ and ‘y’ are said to vary directly with each other, if k = x y for a positive
number, say ‘k’, where ‘k’ is a constant. Therefore, time is in direct proportion with the angle.
We come across many such situations in our day-to-day life, where we get to see the variation in one quantity bringing in a variation in the other quantity. For example:
- 1. If the number of articles purchased increases, the total cost also increases.
- 2. More the money deposited in a bank the more is the interest earned.
Observe that increase in one quantity leads to an increase in the other quantity and therefore we say they are in direct proportion.
To solve such problems, we use the relation x1 y1 = x2 y2
The method by which first we find the value of one unit and then the value of the required number of units is known as the Unitary Method. Consider the question:
Rishi bought 12 registers for Rs 156, find the cost of 7 such registers.
Cost of 12 registers = ₹156. Therefore, the cost of one register = 156 ÷ 12 = ₹13
Therefore, the cost of 7 registers = ₹13 × 7 = ₹91
Inverse Proportion
Let us look at the following situation. Amita can go to her school in four different ways. She can walk, run, cycle, or go by car.
If she,
- Walks at a speed of 3 km/hr she reaches school in 54 minutes.
- Goes to school running at the speed of 6 km/hr she reaches her school in 27 minutes.
- Goes to school by cycling at a speed of 9 km/hr she reaches her school in 18 minutes.
- Goes by car at a speed of 45 kilometres per hour she reaches her school in 3.6 minutes.

Observe that as the speed increases, the time taken to cover the same distance decreases.
If we represent the speed as ‘x’ and the time taken as ‘y’, then as ‘x’ increases, ‘y’ decreases, and vice-versa. It is important to note that the product of ‘x’ and ‘y’ remains constant.
If the value of a variable ‘x’ decreases or increases upon the corresponding increase or decrease in the value of the variable ‘y’, then we can say that variables ‘x’ and ‘y’ are in inverse proportion.
There exists a relation xy = k between them, ‘k’ being constant.
When ‘x’ and ‘y’ are in inverse proportion, we can write:

(y1, y2 and x1, x2 are the corresponding values of ‘y’ and ‘x,’ respectively)
When ‘x’ and ‘y’ are in inverse proportion (or vary inversely), they are also written as:
x ∝ 1 y
Take a squared paper and arrange the 36 counters on it in a different number of rows as shown below.

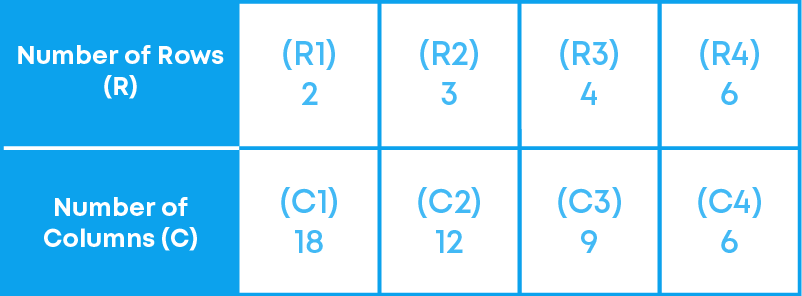
What do you observe? As R increases, C decreases.
Is R1 : R2 = C2 : C1?
R1 : R2 = 2 : 3
C2 : C1 = 12 : 18 = 2 : 3
Thus, R1 : R2 = C2 : C1
Is R3 : R4 = C4 : C3?
R3 : R4 = 4 : 6 = 2 : 3
C4 : C3 = 6 : 9 = 2 : 3
Thus, R3 : R4 = C4 : C3
Are R and C inversely proportional to each other?
We see that R1 : R2 = C2 : C1 and R3 : R4 = C4 : C3
Therefore, R and C are inversely proportional to each other.
We come across many such situations in our day-to-day life, where we see a variation in one quantity bringing in a variation in the other quantity. For example:
- As the speed of a vehicle increases, the time taken to cover the same distance decreases.
- For a given work, more the number of workers less will be the time taken to complete the work.
Observe that an increase in one quantity leads to a decrease in the other quantity and therefore we can say they are in inverse proportion.
To solve such problems, we use the relation x1y1 = x2y2
Common Errors
The following are topics in which students make common mistakes when dealing with direct and inverse proportion:
- 1. Is it a direct proportion if x and y increase together?
- 2. Calculate inverse proportion
Is It A Direct Proportion If x And y Increase Together?
We know that,
- Direct proportion: Two quantities x and y are said to be in direct proportion if they increase or decrease together in such a manner that the ratio of their corresponding values remains constant.
- Inverse proportion: Two quantities x and y are said to be in inverse proportion if an increase in x causes a proportional decrease in y and vice-versa, in such a manner that the product of their corresponding values remains constant.
Now, consider the example given below:
The following table shows the ages of the mother and the daughter.
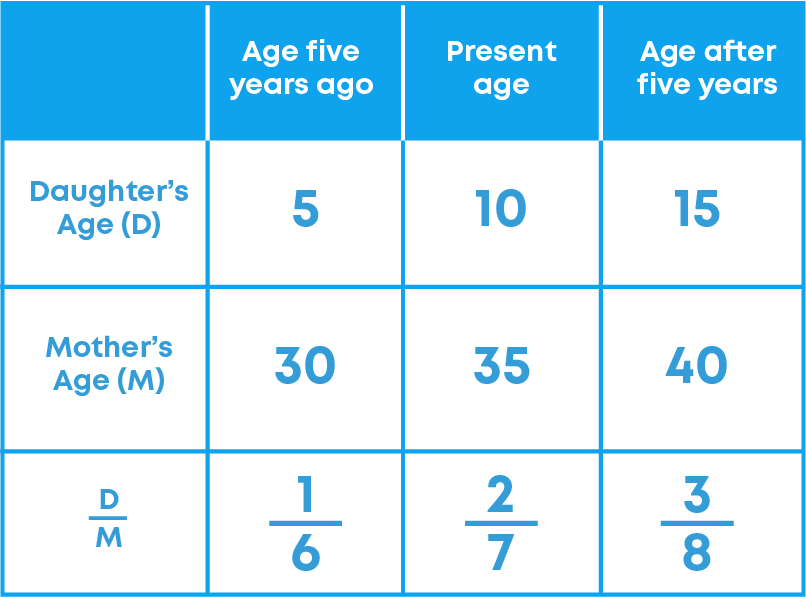
What do you notice? Do the daughter’s age (D) and the mother’s age (M) increase together?
Is D M the same every time? No.
Thus, variables increasing (or decreasing) together need not always be in direct proportion.
Calculate Inverse Proportion
Consider the example below:
If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
We have the following table:

Observe the two calculations:
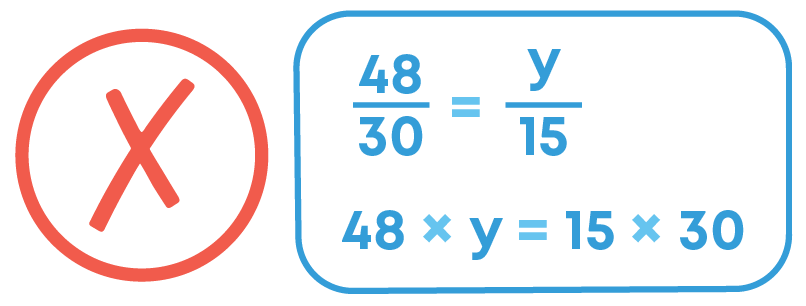
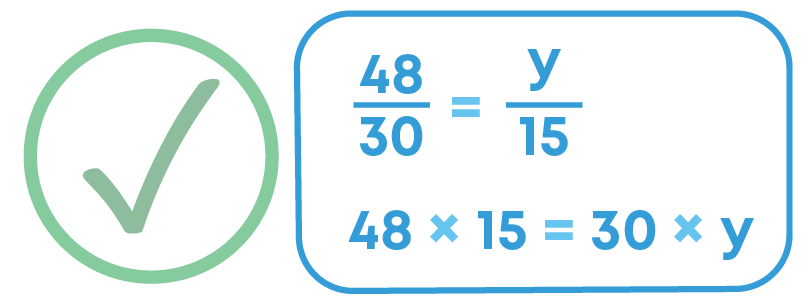
Remark: While solving such problems we cross multiply, that is, numerator of first fraction gets multiplied with denominator of the second fraction.
Conclusion
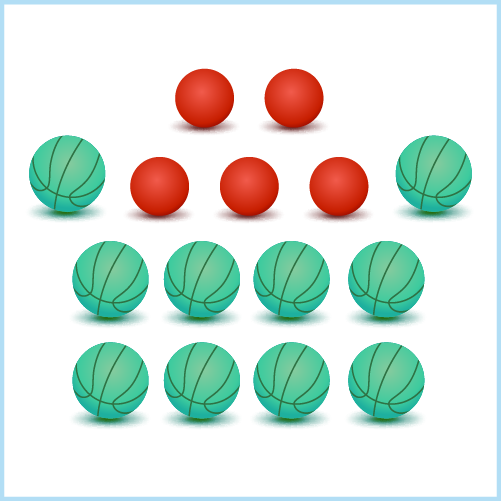
Now that you are familiar with direct and inverse proportion, can you solve the riddle below?
Find the odd one out if the number of red and green balls are in direct proportion.
a.

b.

c.
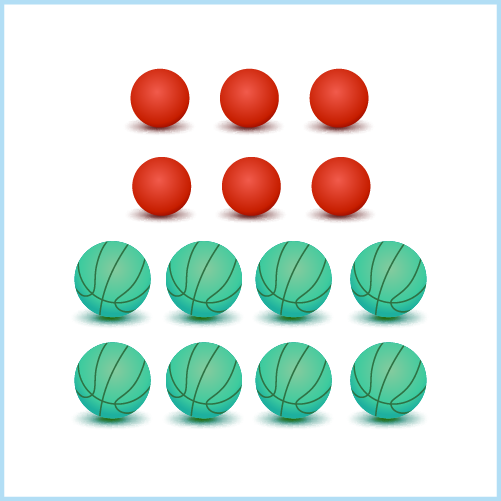
d.