Introduction
Fraction is a number representing equal parts of a whole. The whole may be a single object or a group of objects. For example, look at this circle. It is divided into 3 equal parts.
Look at the fraction 3/8. It has two parts - Numerator and Denominator.
- The numerator tells us the number of parts considered. In the above example, it is the number of slices of pizza that you ate.
- The denominator tells us the total number of equal parts in the whole. This is the total number of slices in your pizza.
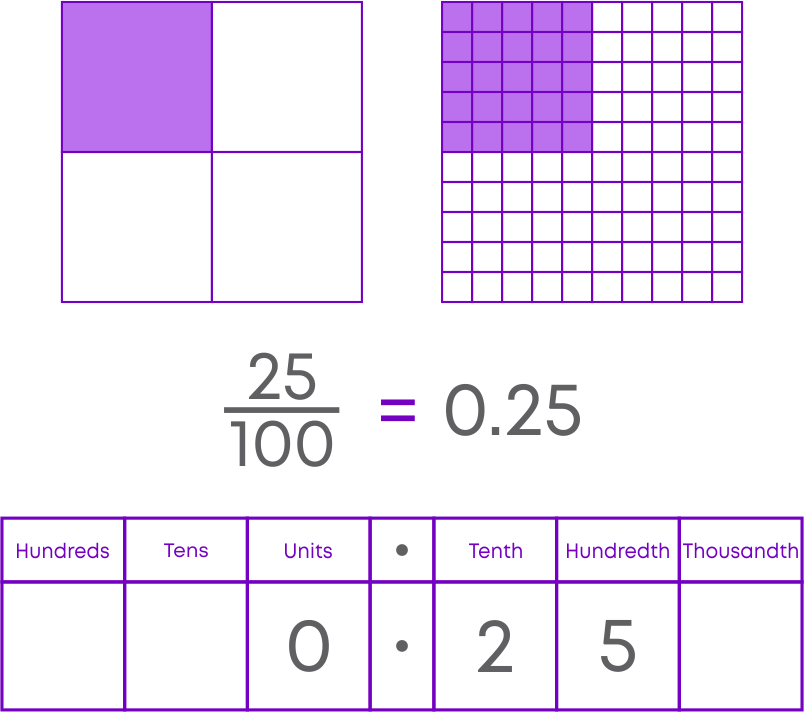
Decimal numbers are special fractions whose denominator is 10, 100, 1000 etc. For example, a square is divided into 4 equal parts. Shaded part represents 1/4 of the square.
The same square is divided into 100 parts. Here the shaded part represents 25/100.
The fraction 25/100 can be represented as the decimal number 0.25.
You have learnt about fractions and decimals in your earlier classes. Let us understand where fractions and decimals are used in real life. Watch the video below.
Concepts
The chapter ‘Fractions and Decimals’ covers the following concepts:
Multiplication of Fractions
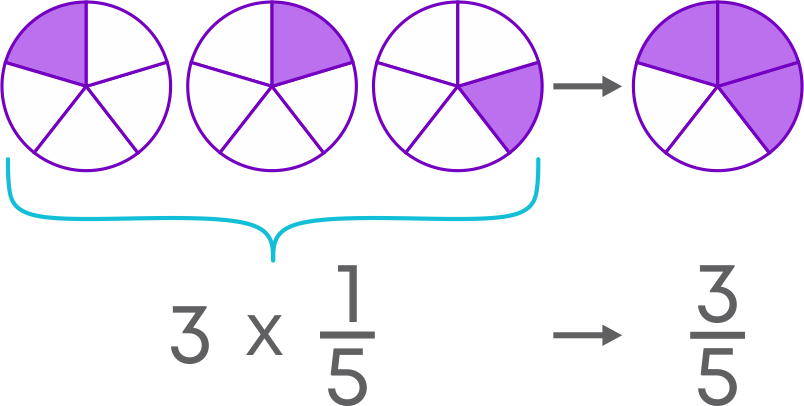
Let us visualise multiplication of fraction by whole number pictorially. For example, consider 3 × 1/5. As you know, multiplication is nothing but repeated addition. Hence,
3 × 1/5 = 1/5 + 1/5 + 1/5 = 3/5
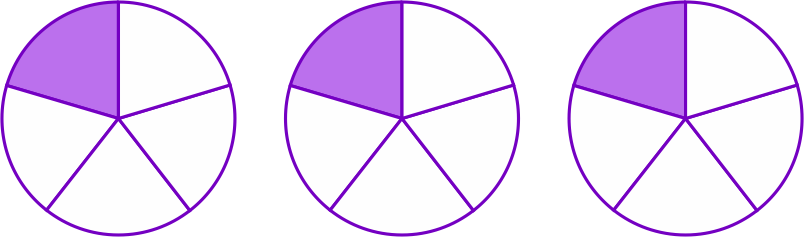
Look at these circles.
They are circles of the same size. The shaded part of each of the given circle represents the fraction 1/5.
Now we have 3 of them. This means that these three circles represent 3 × 1/5 = 1/5 + 1/5 + 1/5 = 3/5.
We can represent the multiplication of the proper fraction 15 and the whole number 3 using this representation.
Take another example:
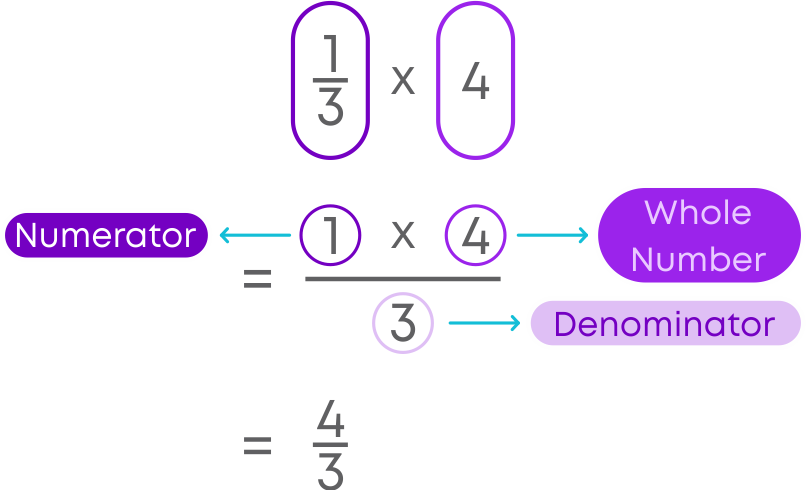
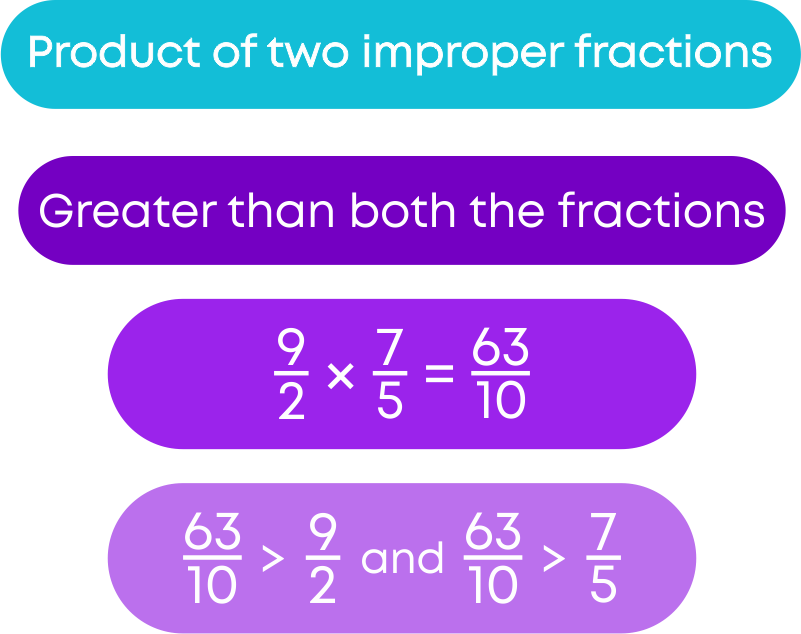
Let us see how to multiply an improper fraction by a whole number.
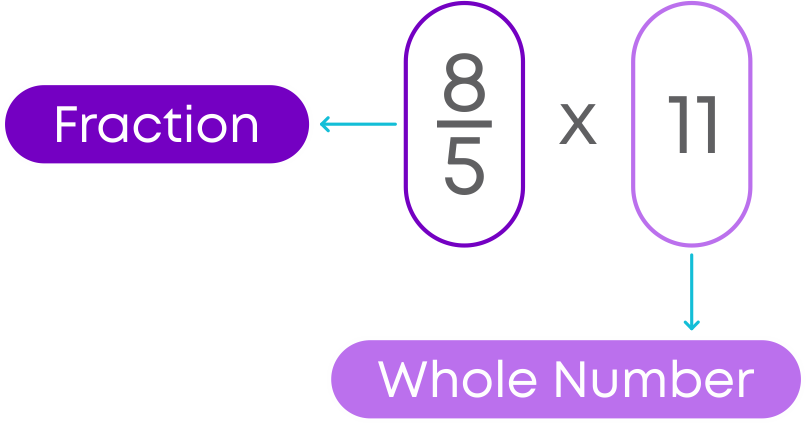
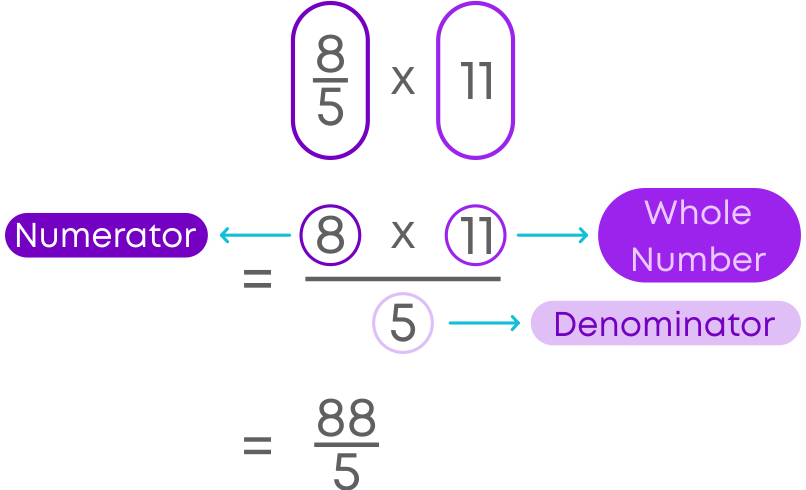
To multiply them:
- Multiply the numerator of the fraction by the whole number.
- Keep the denominator same.
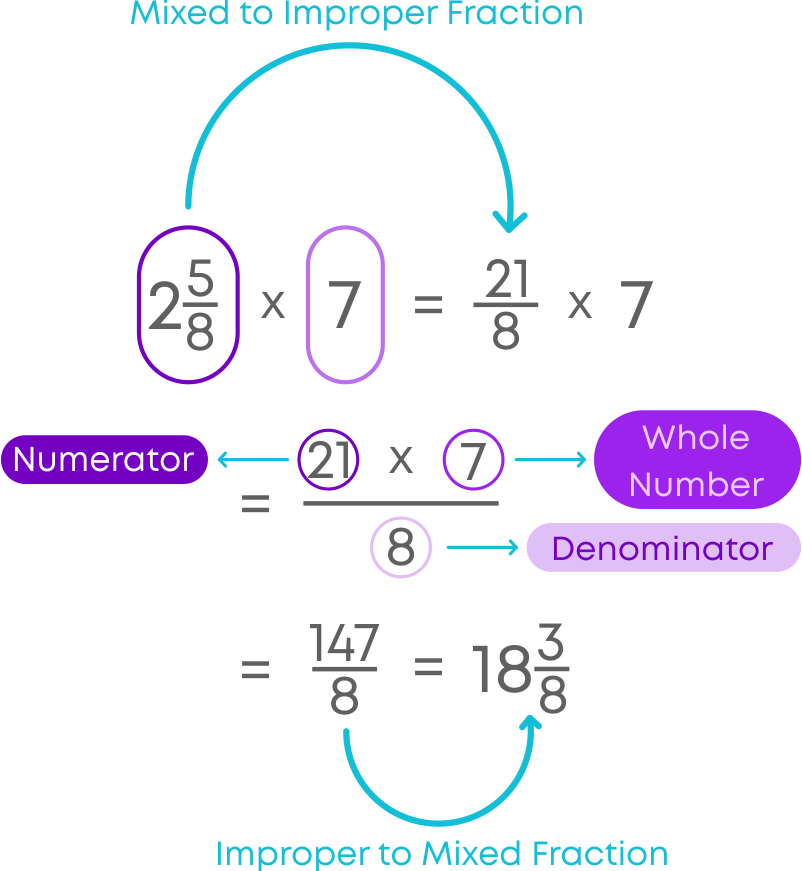
We will see how to multiply a mixed fraction by a whole number.
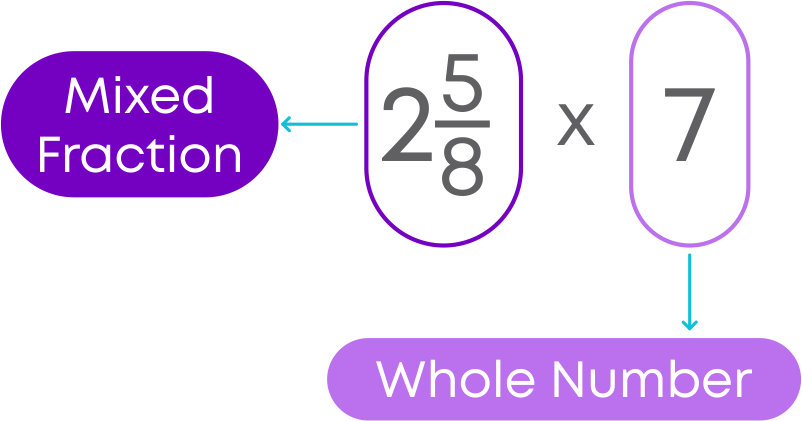
- Convert the mixed fraction into improper fraction.
- Multiply the whole number by the numerator of fraction.
- Convert the resultant fraction to a mixed fraction.
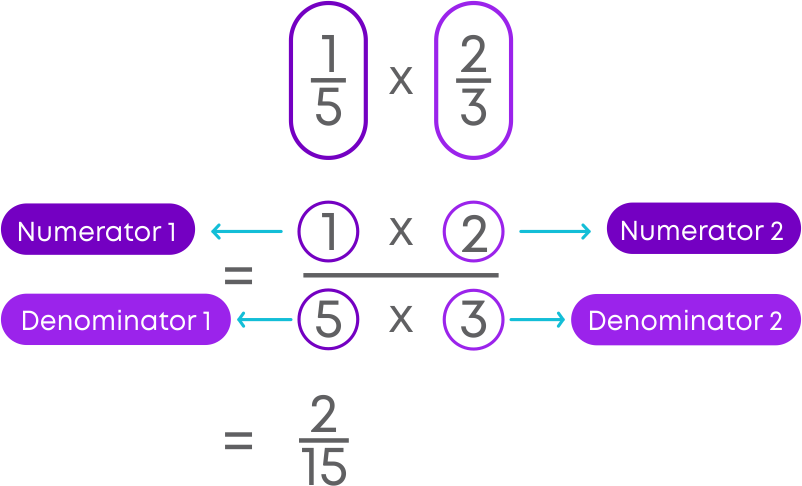
You know how to multiply a fraction and a whole number. Now let us see how to multiply two fractions.
To multiply follow these steps
- Multiply the numerator of the first fraction by the numerator of the second fraction.
- Multiply the denominator of the first fraction by the denominator of the second fraction.
Now, let us learn multiplication of fractions with the operator ‘of.’
There are 15 balloons. Diya wants to use 1/3rd of the balloons for decorating her classroom. Diya wants to know how many balloons does she need?
To know this, Diya needs to find what is one-third of 15.
In the example above, the fraction 1/3 acts as an operator on the total number of balloons. 1/3 of 15 gives the number of balloons in each group when 15 is divided into 3 groups.
Did you also notice that:
15 × 1/3 = 1 ×15/3 = 15/3 = 5
Hence, we can conclude that, for fractions, the ‘of’ operator works the same way as multiplication.
Remember these points:
Division of Fractions
Reciprocal of a fraction is obtained by inverting the numerator and denominator of the fraction. For example, the reciprocal of 5/3 is 3/5. Remember, reciprocal of 1 is 1, and 0 does not have a reciprocal. Follow these steps to write the reciprocal of mixed fraction 3 1⁄2 :
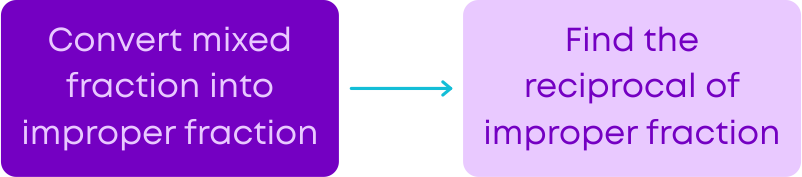
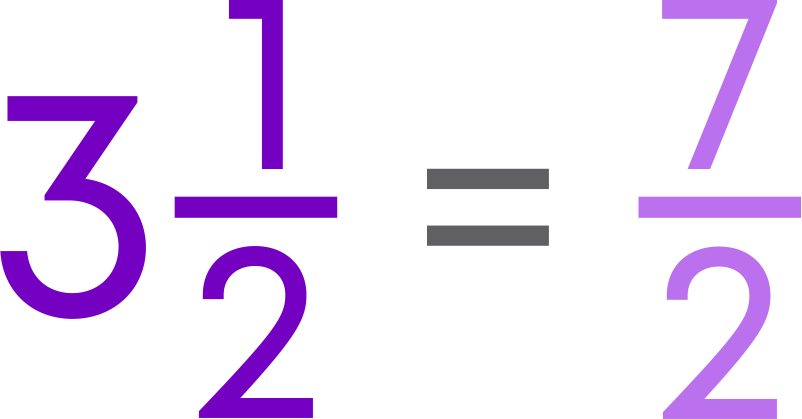
Reciprocal of 7/2 = 2/7
Hence, the reciprocal of 3 1⁄2 = 2/7
To divide a whole number by any fraction, multiply that whole number by the reciprocal of that fraction.
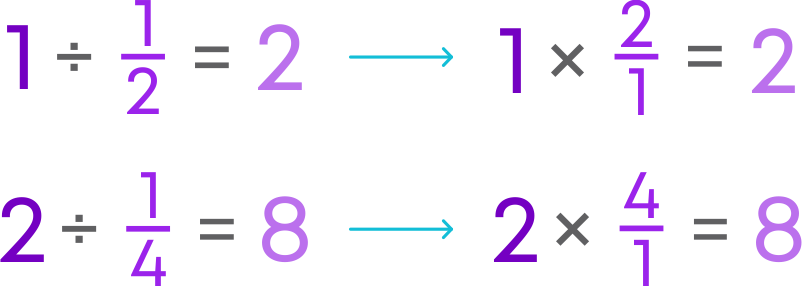
Let us see how to divide a whole number by a proper fraction or an improper fraction.
To divide a whole number by a fraction, multiply the whole number by the reciprocal of that fraction.
If the resultant fraction is an improper fraction, convert it to a mixed fraction.
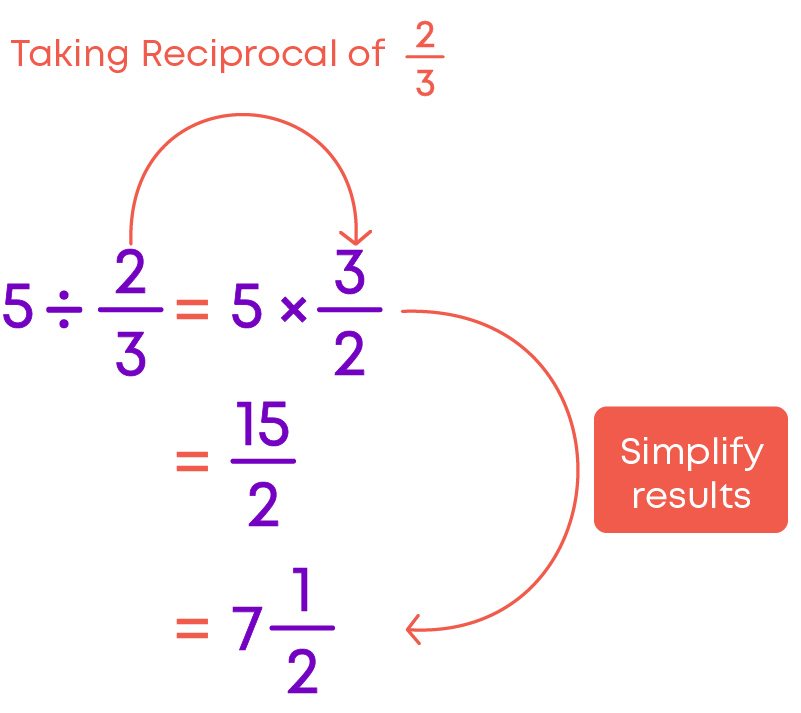
Hence, 5 ÷ 2/3 = 7 1⁄2
Let us see how to divide a whole number by a mixed fraction.
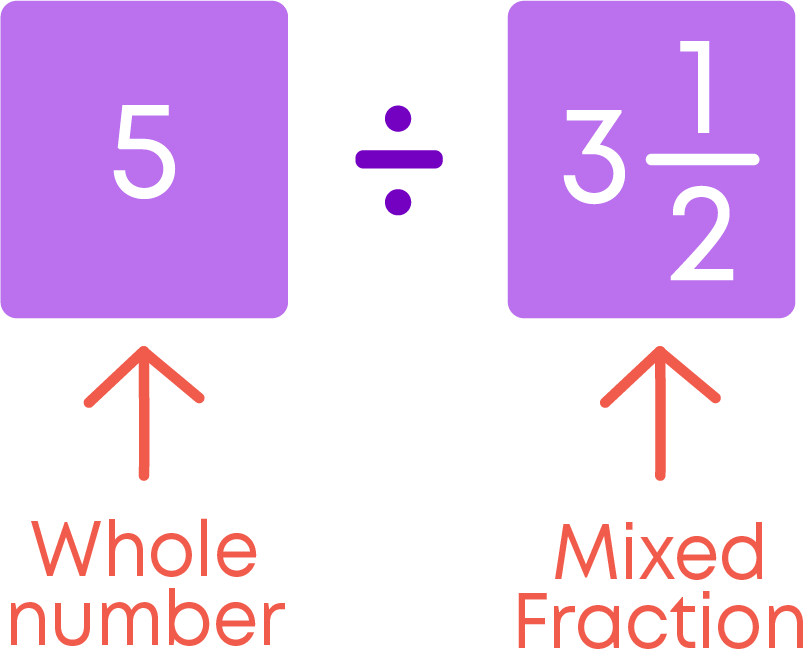
To divide a whole number by a mixed fraction:
- Convert the mixed fraction to an improper fraction.
- Multiply the whole number by the reciprocal of the mixed fraction.
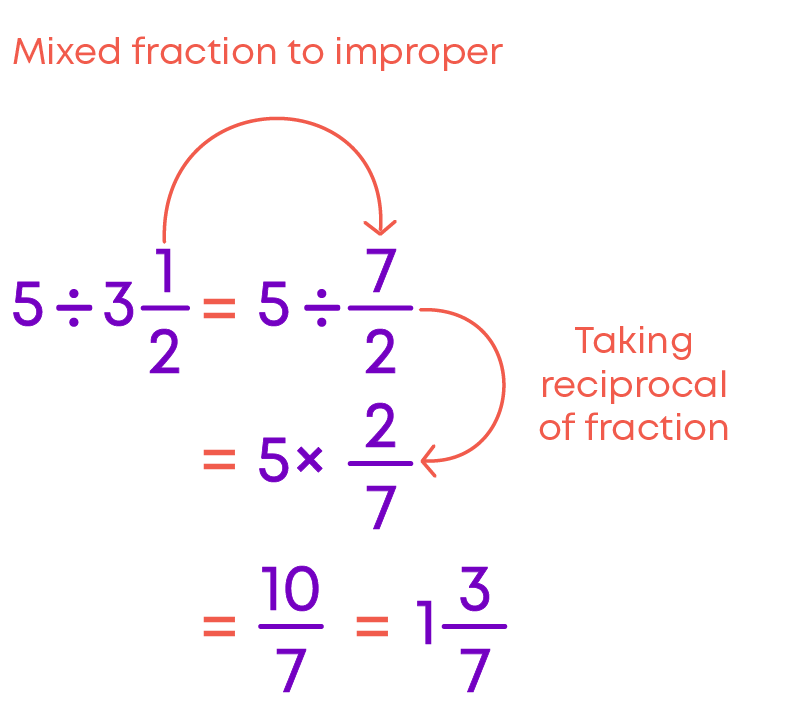
Let us see how to divide a proper or an improper fraction by a whole number.
To divide a fraction by a whole number
- Find the reciprocal of the whole number.
- Multiply the fraction by the reciprocal of the whole number.
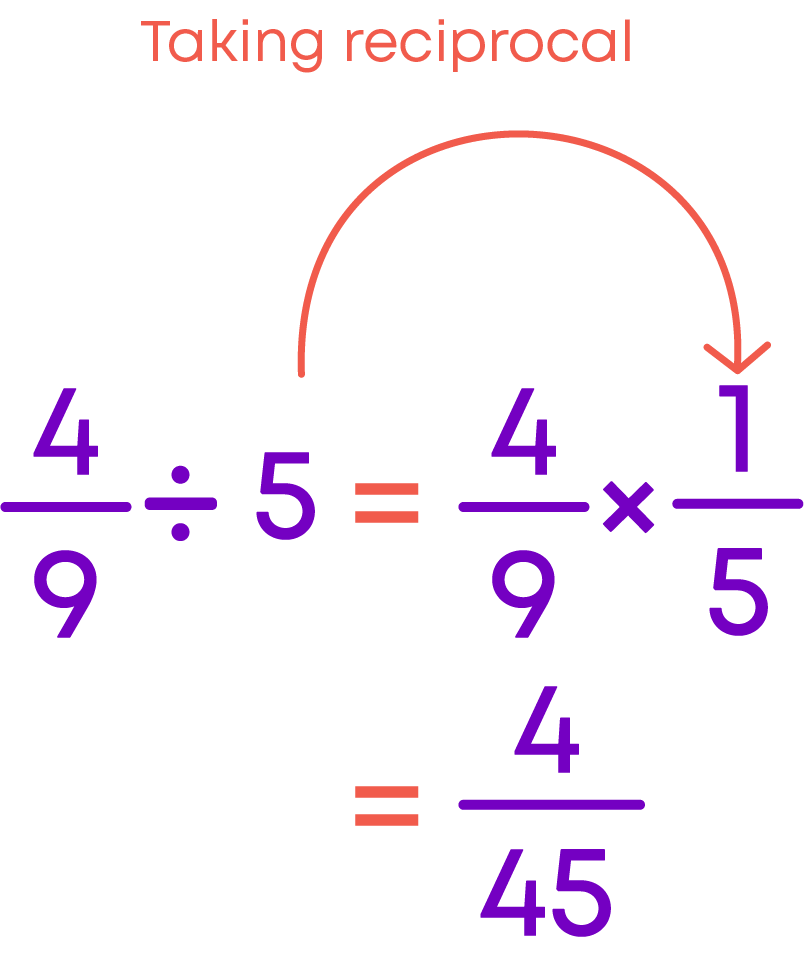
Hence, 4/9 ÷ 5 = 4/45
Let us see how to divide a mixed fraction by a whole number.
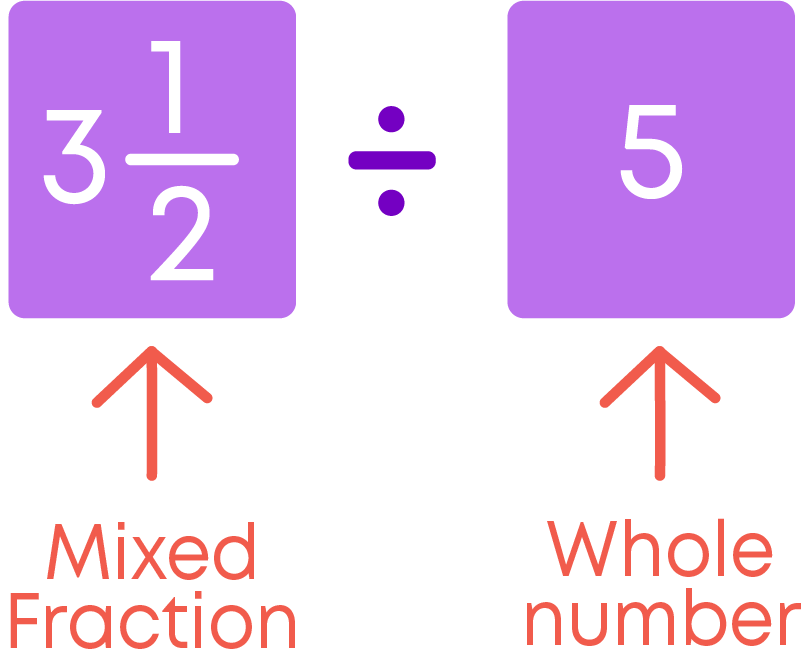
To divide a mixed fraction by a whole number
- Find the reciprocal of the whole number.
- Convert the mixed fraction to an improper fraction.
- Multiply the improper fraction by the reciprocal of the whole number.
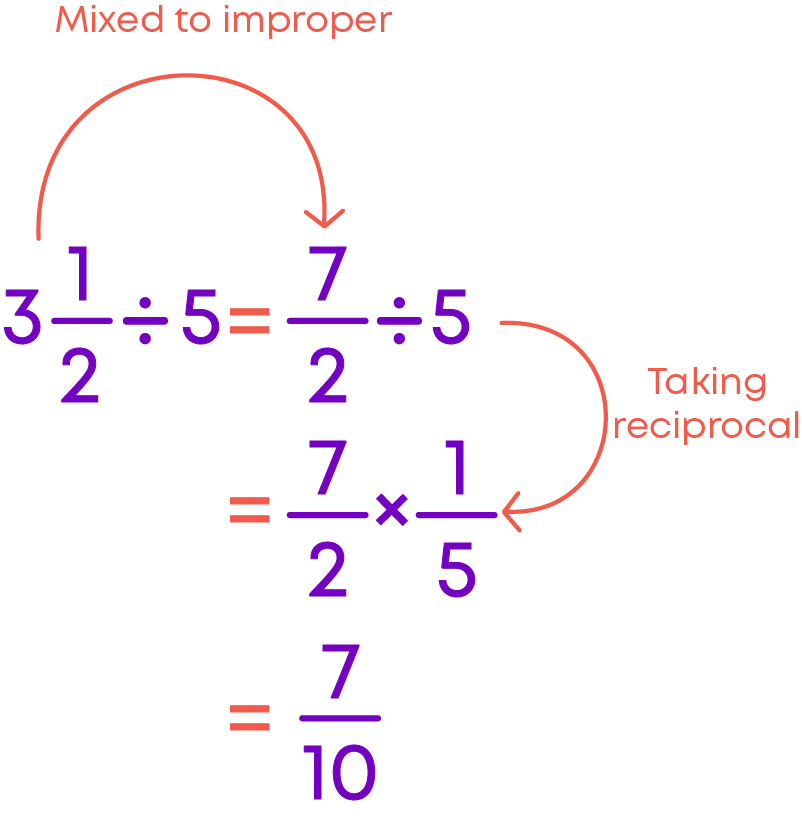
Now, let us see how to divide a fraction by another fraction.
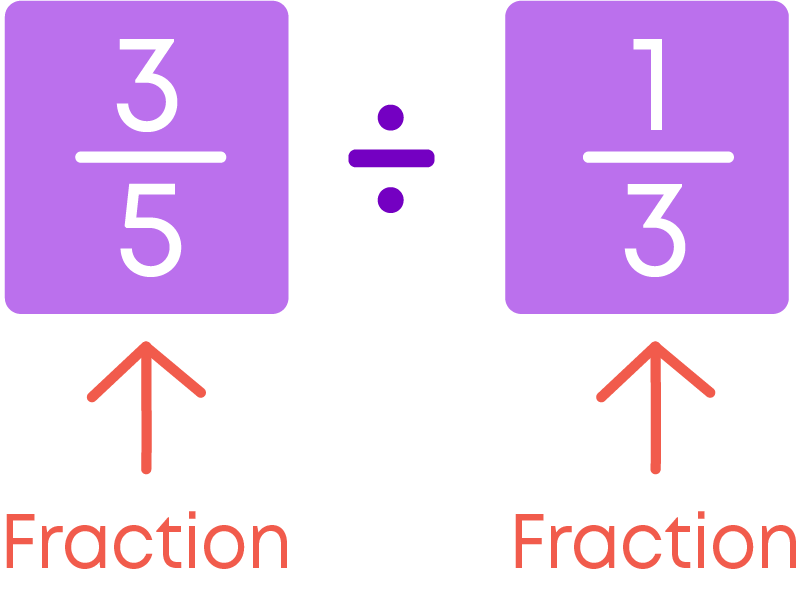
To divide a fraction by another fraction,
- Find the reciprocal of the divisor.
- Multiply the dividend by the reciprocal of divisor.
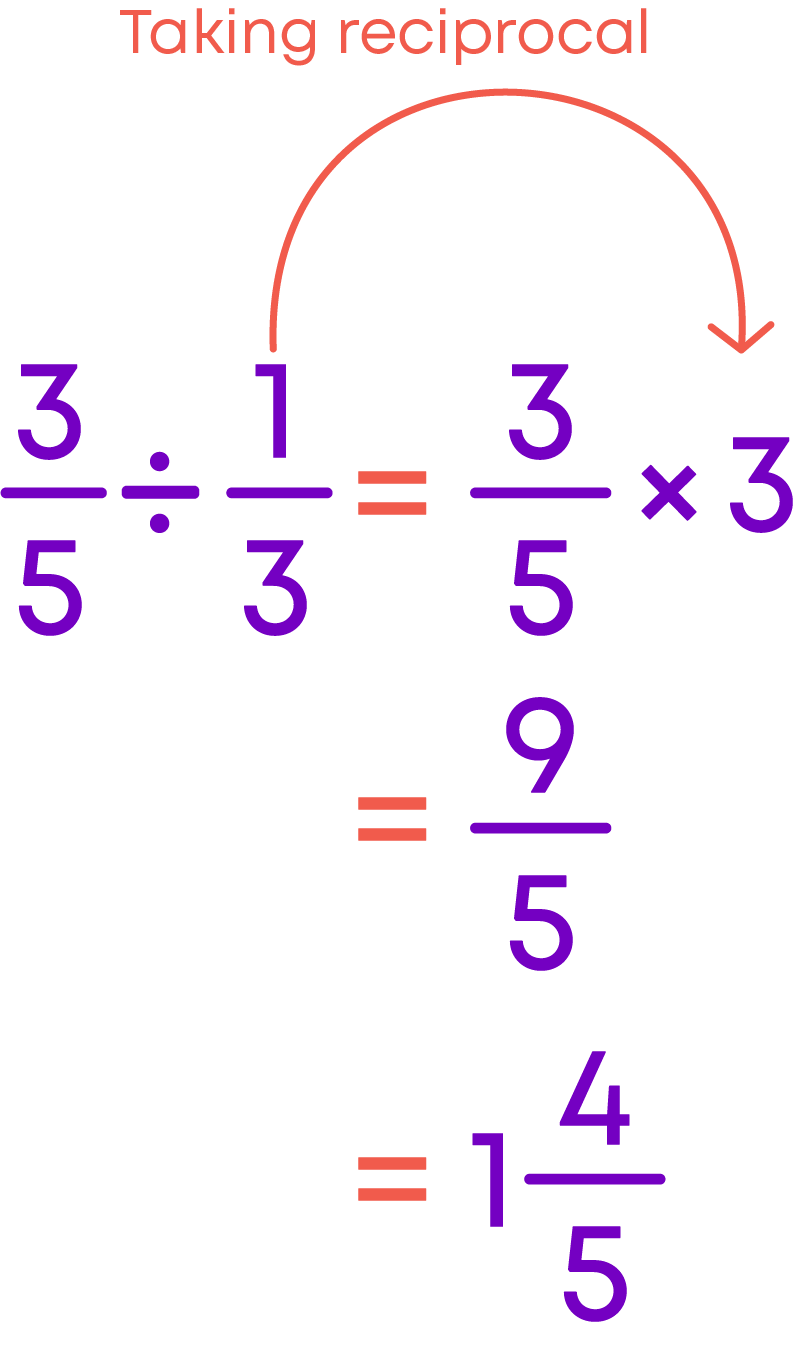
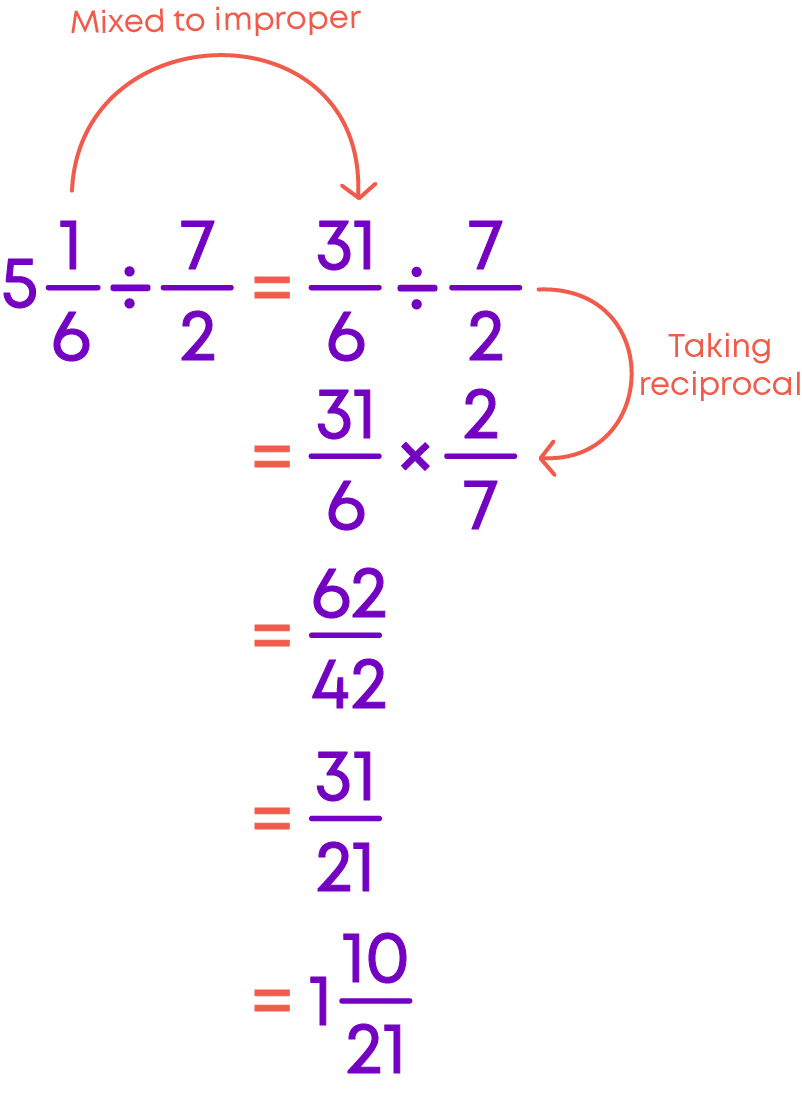
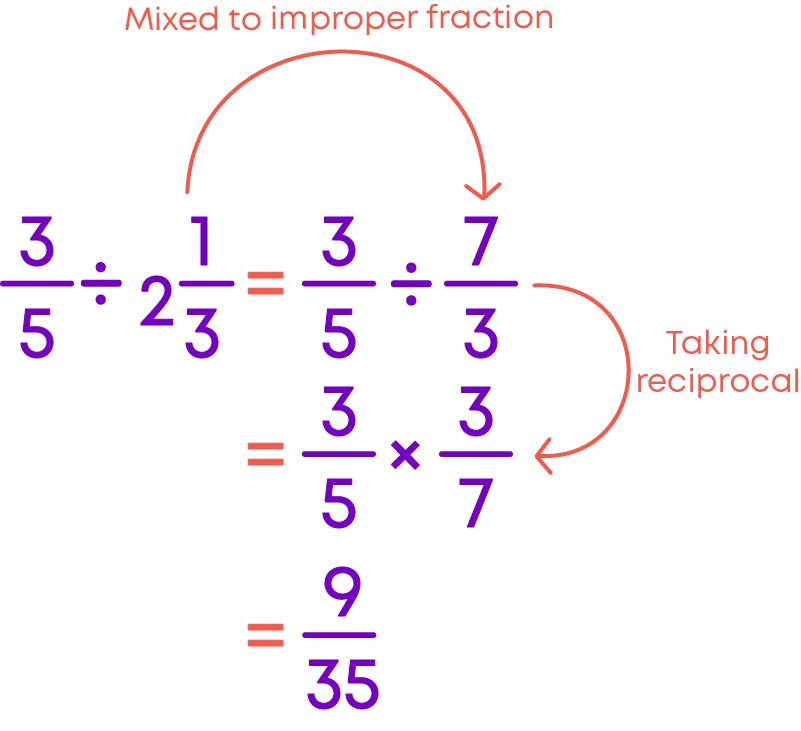
Let us see how to divide a mixed fraction by a proper or an improper fraction.
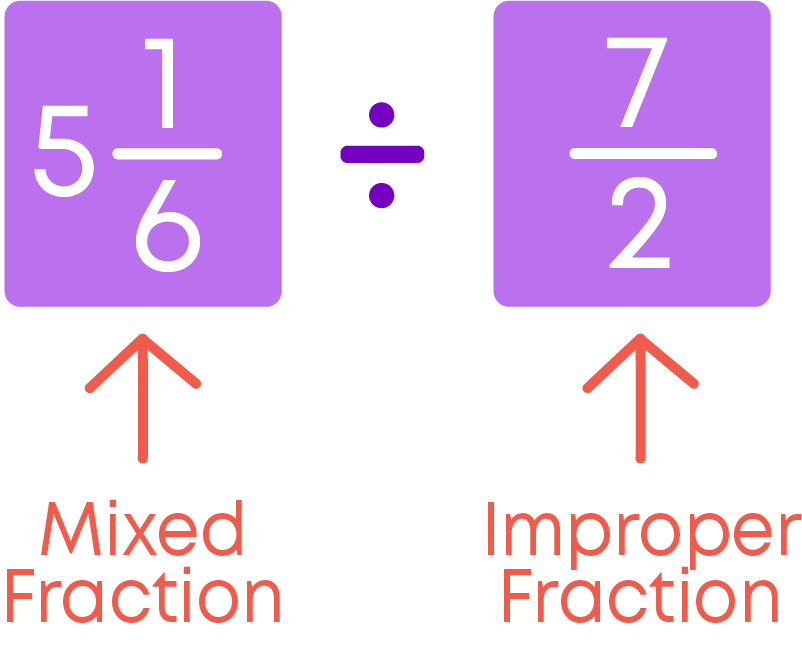
To divide a mixed fraction by a proper/improper fraction
- Convert the mixed fraction to an improper fraction.
- Find the reciprocal of the divisor.
- Multiply the improper fraction by the reciprocal of the divisor.
Let us see how to divide a proper or an improper fraction by a mixed fraction.
To divide a proper or improper fraction by a mixed fraction
- Convert the mixed fraction to an improper fraction and find its reciprocal.
- Multiply the proper/improper fraction by the reciprocal of the mixed fraction.
Multiplication of Decimal Numbers
We know how easy it is to multiply a whole number by 10, 100, 1000 etc. For example, let us take the number 37.
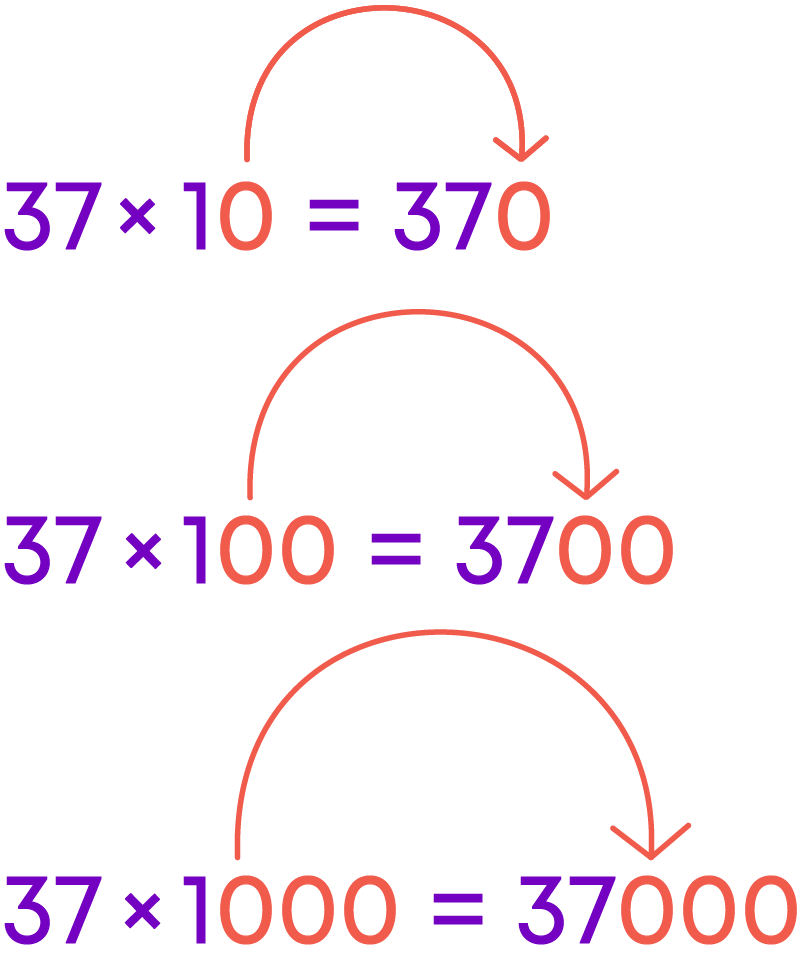
But how do we multiply decimal numbers? Let us find out. Consider the decimal number 5.37:
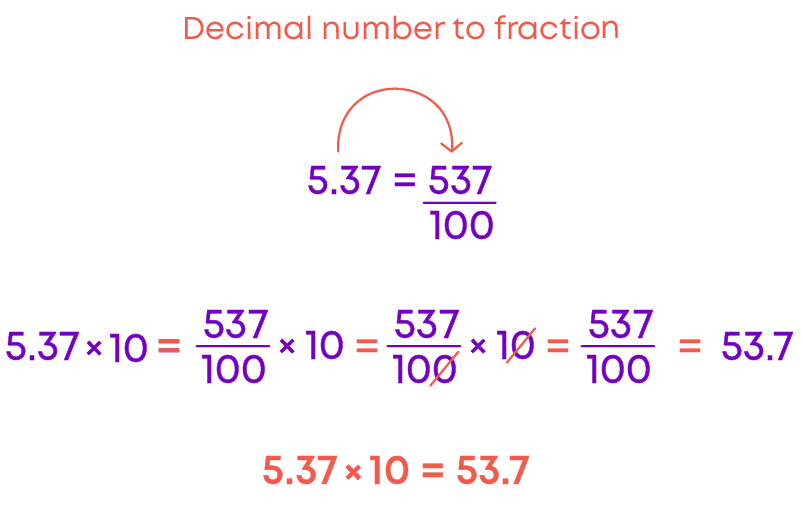
Did you notice that when 5.37 is multiplied by 10, the number 537 gets converted from hundredth part to tenth? That is why the decimal point is shifted one place to the right.
Now let us multiply 5.37 by 100 and 1000.
In short,
- 5.37 × 10 = 53.7
- 5.37 × 100 = 537
- 5.37 × 1000 = 5370
Do you notice a pattern here?
To multiply a decimal number by 10, shift the decimal point to the right by one place. To multiply a decimal number by 100, shift the decimal point to the right by two places. To multiply a decimal number by 1000, shift the decimal point to the right by three places.
You know how to multiply a decimal number by 10, 100, 1000 etc. Let us multiply 2.45 by 6:
We can see that 2.45 = 245/100
2.45 × 6 = 245/100 × 6 = 245 ×6 / 100 = 1470100 = 14.70
Hence, 2.45 × 6 = 14.7
The product of a whole number and a decimal number will have the same number of decimal places as that of the decimal number being multiplied.
Follow these steps to multiply a decimal number by a whole number:
Now let us multiply 12.5 × 3.32.
We can see that 12.5 = 125/10 and 3.32 = 332/100
Hence, 12.5 × 3.32 = 12/510 × 332/100 = 41500/1000 = 41.50
When two decimal numbers are multiplied, the number of decimal places in the product will be the sum of the decimal places of the numbers being multiplied.
Follow these steps to multiply a decimal number by another decimal number:
Division of Decimal Numbers
We know how easy it is to divide a whole number by 10, 100, 1000 etc. For example, let us take the number 54,000.
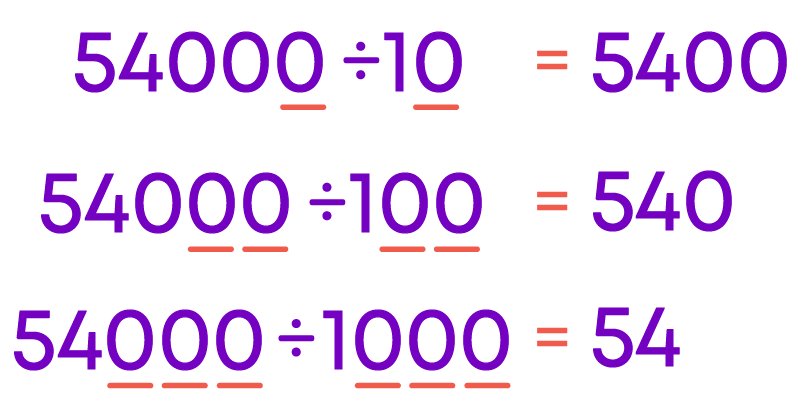
But how do we divide decimal numbers? Let us find out. Consider the decimal number 23.5 divided by 10.
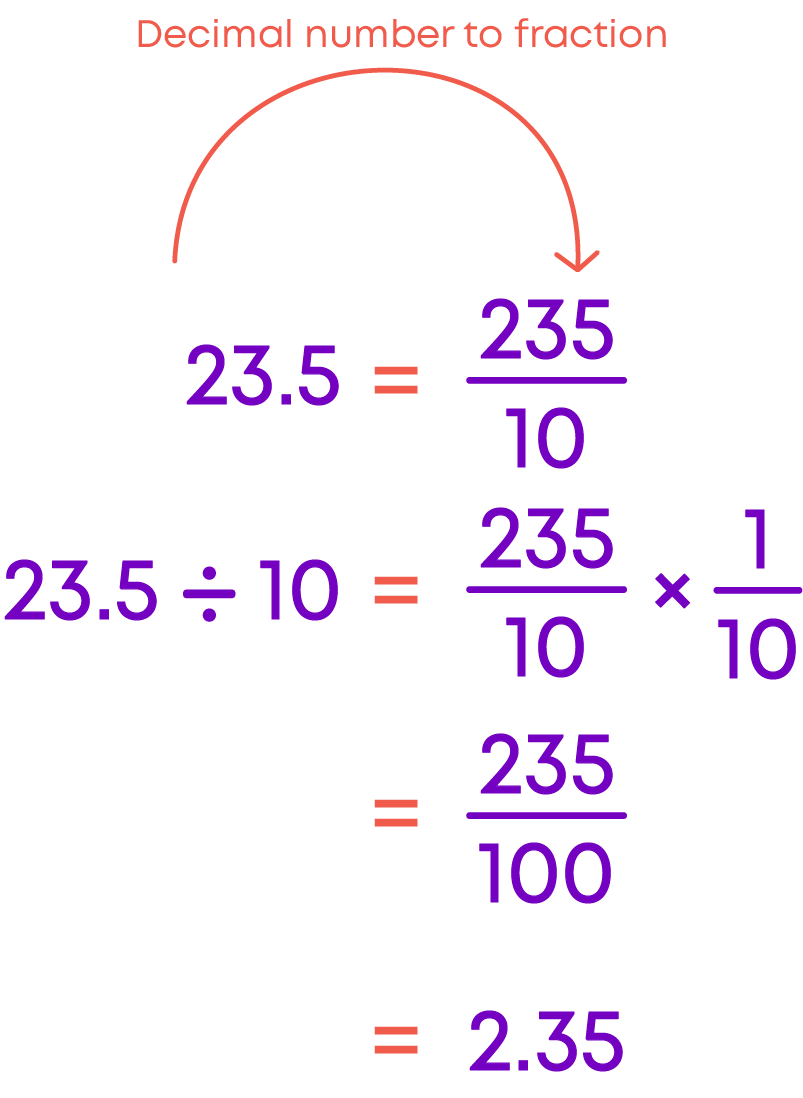
Did you notice that when 23.5 is divided by 10, the number 235 gets converted from tenth part to hundredth part? That is why the decimal point is shifted one place to the left.
Let us divide 23.5 by 100 and 1000:
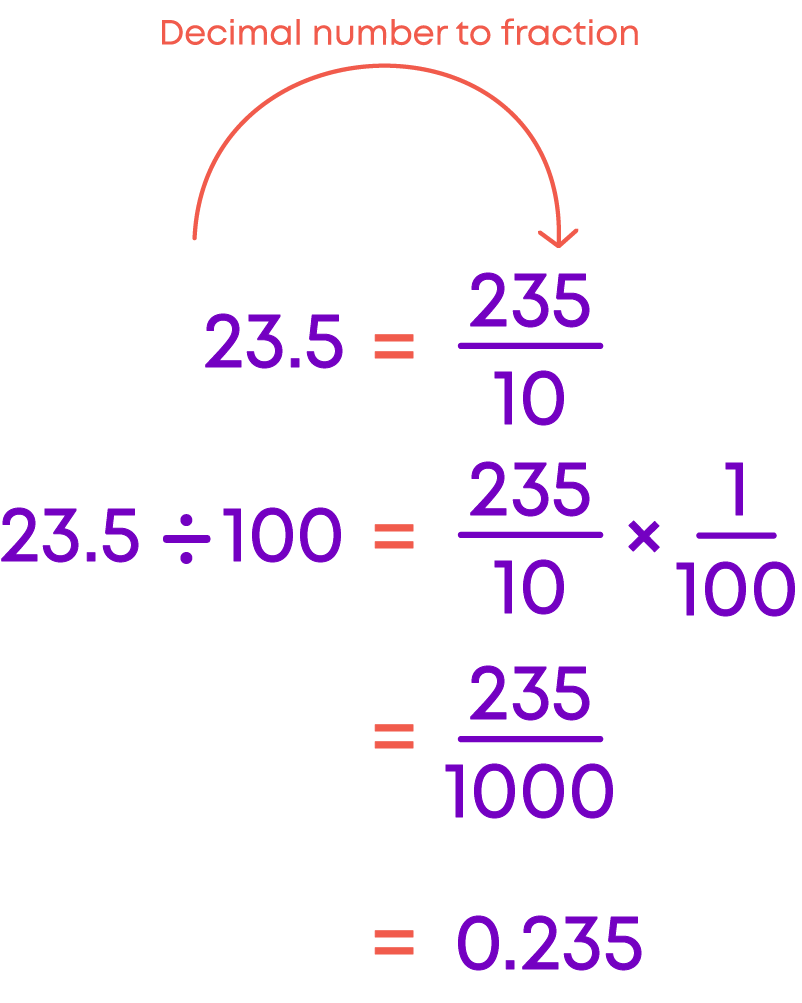
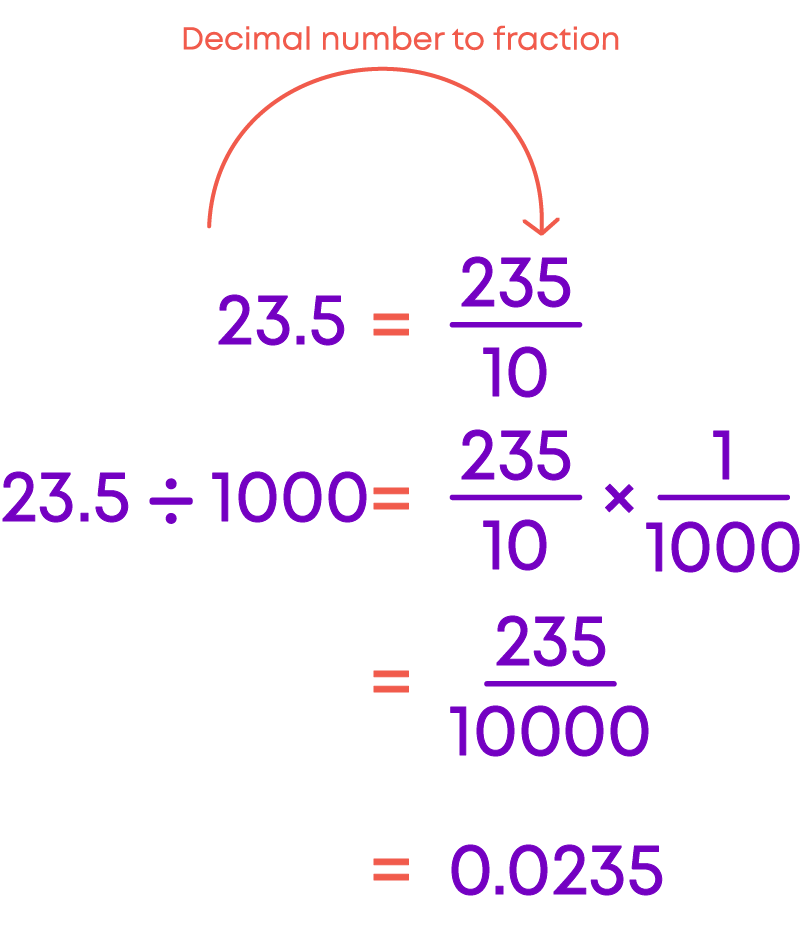
In short,
- 23.5 ÷ 10 = 2.35
- 23.5 ÷ 100 = 0.235
- 23.5 ÷ 1000 = 0.0235
Did you notice the pattern here?
To divide a decimal number by 10, shift the decimal point to the left by one place. To divide a decimal number by 100, shift the decimal point to the left by two places. To divide a decimal number by 1000, shift the decimal point to the left by three places.
You know how to divide a decimal number by 10, 100, 1000 etc. Let us learn how to divide a decimal number by a whole number.
To divide a decimal by a whole number
- Perform long division method like the division of whole numbers.
- If there is a decimal point before any digit that is to be brought down from the dividend, place a decimal point in the quotient before doing so.
We saw how to divide 8.48 by 4.
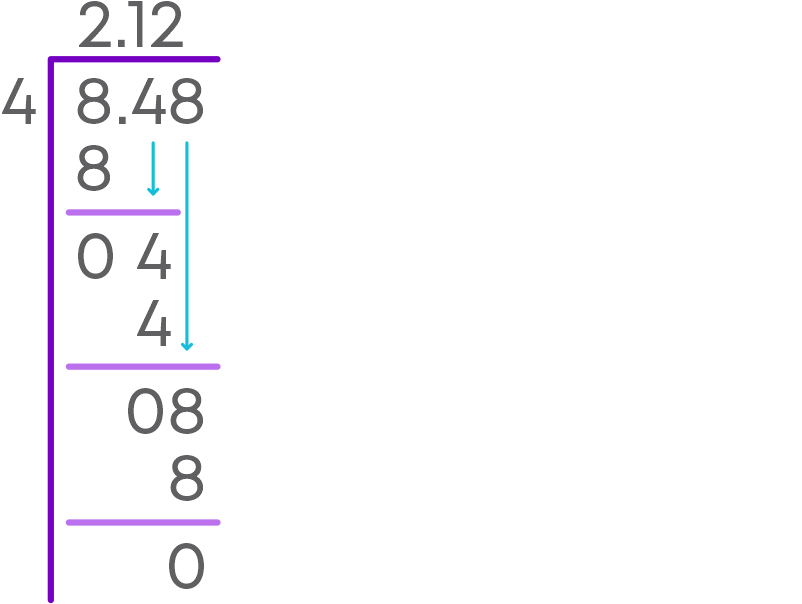
8.48 ÷ 4 = 2.12.
We also saw how to divide 163.25 by 8.
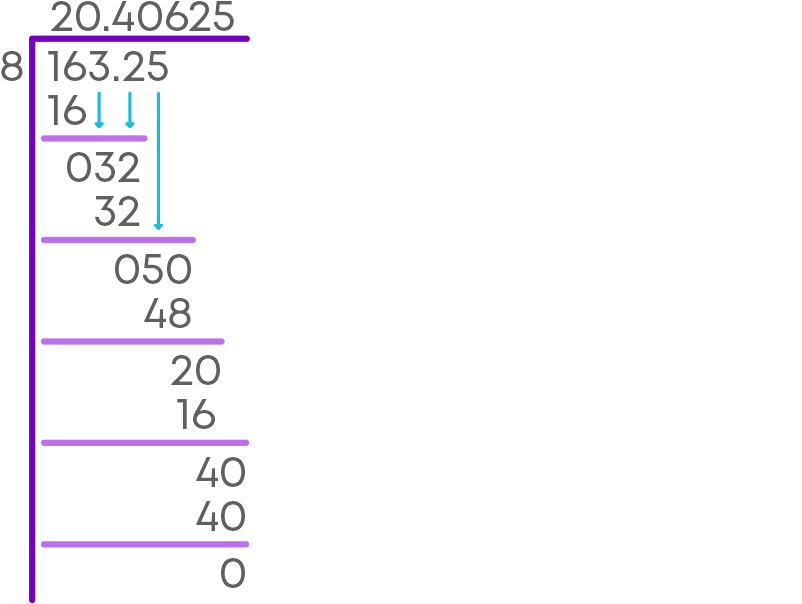
163.25 ÷ 8 = 20.40625.
How to divide a decimal number by another decimal number? For example, divide 8.48 by 0.4.
Convert the divisor into a whole number by multiplying both the dividend and the divisor by the powers of 10.
8.48 ÷ 0.4 = 8.48/0.4 = 8.48 ×10/0.4 ×10 = 84.8/4 = 84.8 ÷ 4
Perform long division method similar to the division of decimal numbers by whole numbers.
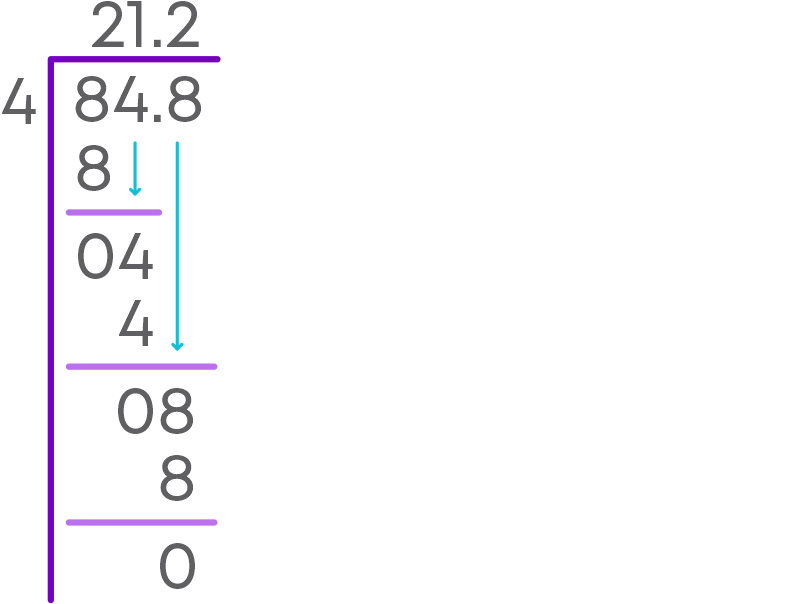
Hence, 8.48 ÷ 0.4 = 84.8 ÷ 4 = 21.2.
Common Errors
The following are topics in which students make common mistakes when dealing with fractions and decimals:
- 1. Multiply a fraction and a whole number
- 2. Cancelling out common factors
- 3. Finding the reciprocal of the correct fraction
- 4. Multiplication and division of decimal numbers by powers of 10
- 5. Placing decimal points in multiplication
- 6. Placing decimal points while dividing
Multiply A Fraction And A Whole Number
What is 3/4 × 10?
When you multiply a fraction by a whole number, the whole number gets multiplied to the numerator of the fraction. Hence, 3/4 × 10 = 3 ×10/4 = 30/4
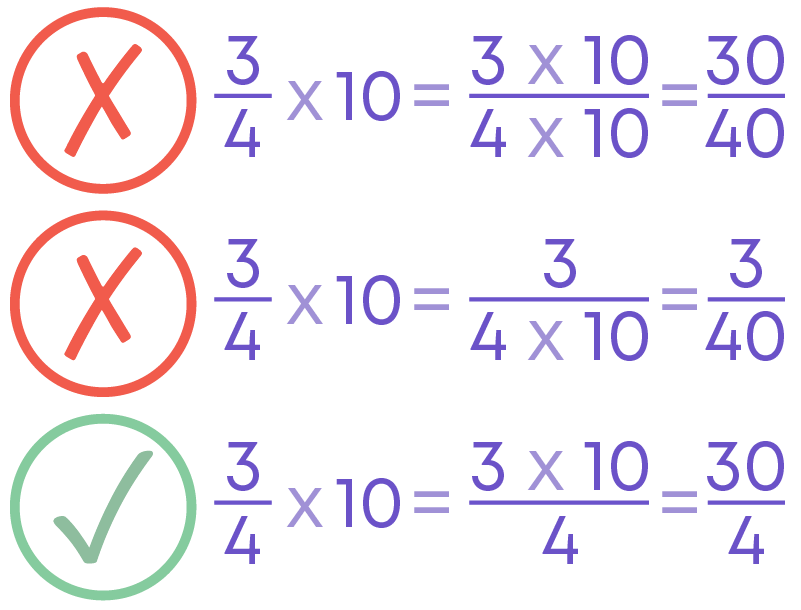
Cancelling Out Common Factors
Consider 3/8 × 12.
3 and 12 have common factors. Can we cancel them? No! The whole number 12 can be written in a fractional form as 12/1 and not 1/12.
Both 12 and 3 are the numerators and we cannot cancel their common factors.
Meanwhile, common factors of 8 and 12 can be cancelled as 8 is in the denominator and 12 is in the numerator.
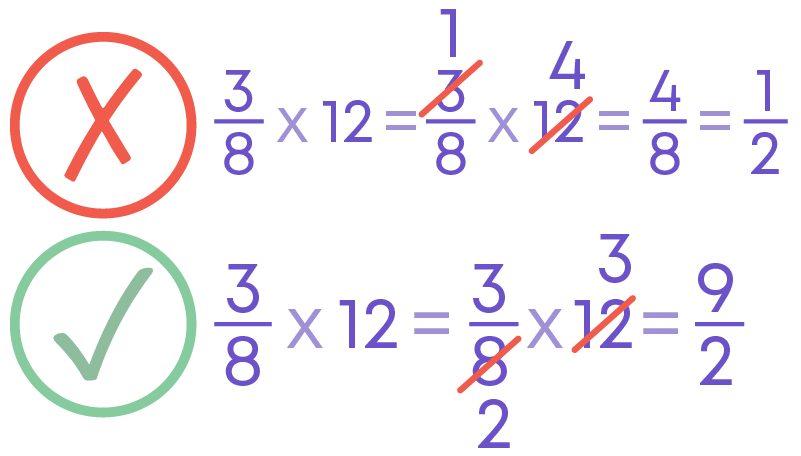
Finding The Reciprocal Of The Correct Fraction
We know that division of fractions is the same as multiplication by the reciprocal. Care should be taken that it is the reciprocal of the divisor and not the dividend.
For example, consider 4/9 ÷ 1/3.
Dividing 4/9 by 1/3 is the same as multiplying 4/9 by the reciprocal of 1/3.
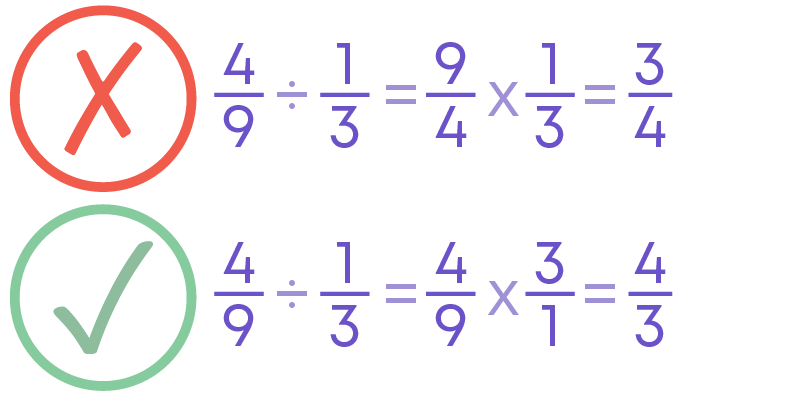
Multiplication And Division Of Decimal Numbers By Powers Of 10
Consider the decimal number 5.608. To multiply or divide a decimal number by powers of 10, we shift the decimal places.
Care should be taken that the decimal places must be shifted
- Right – For multiplication
- Left – For division.
Let us find out what is 5.608 × 100 and 5.608 ÷ 100.
Do not get confused between LEFT and RIGHT.
Remember that, upon multiplication by powers of 10, the magnitude of the number increases, and you must get a greater number as the answer.
Placing Decimal Points In Multiplication
Do you know how to multiply two decimal numbers?
- Multiply the numbers by ignoring the decimal point.
- The number of decimal places in the product is the sum of the number of decimal places in the multiplicand and the multiplier.
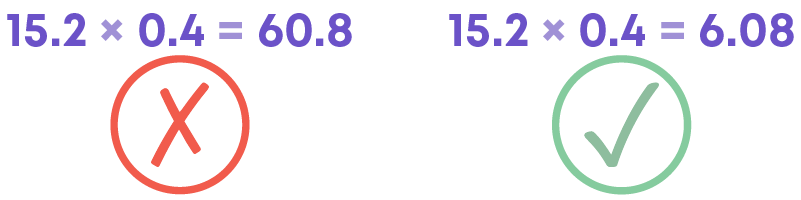
Placing Decimal Points While Dividing
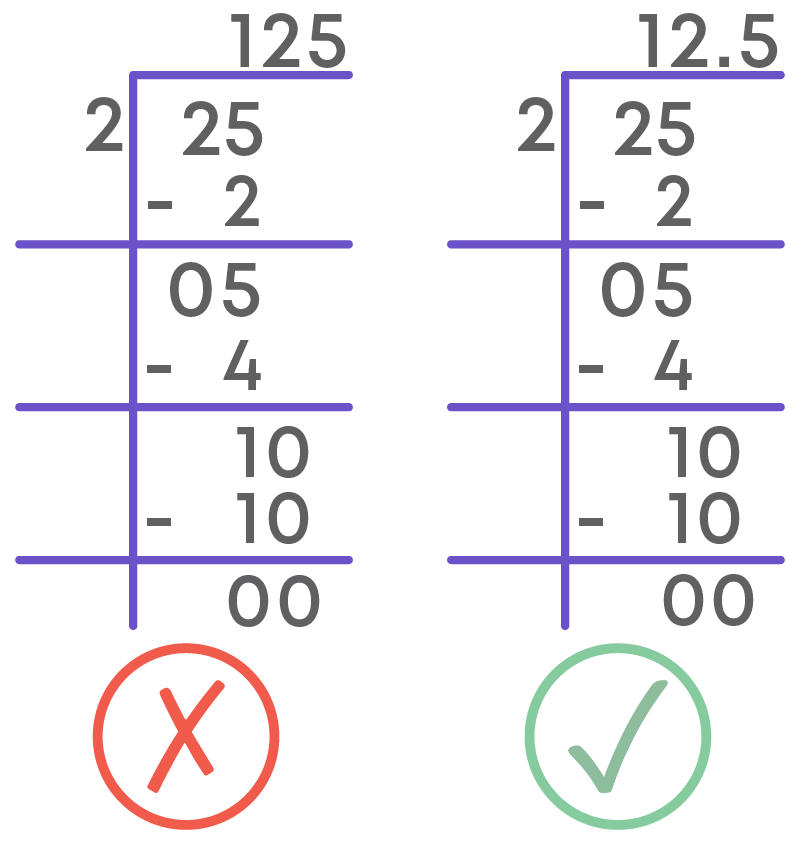
While dividing numbers, we go on with the division till we get ‘0’ as the reminder.
Once the digits in the whole number are exhausted, do not forget to add a decimal point in the quotient before adding ‘0’ to the dividend.
Conclusion
Now you have learnt about multiplication and division of fractions and decimals. Can you solve the puzzle below?
Solve the picture:
Jyothi
Author
A math enthusiast and an educationist, Jyothi has a strong academic background and has demonstrated an impressive history of working in the education industry. Jyothi is skilled in developing and reviewing lesson plans, learning content, assessments, and video story boards and scripts.
