Introduction
If you look closely, you will notice that symmetry is all around us. Some great examples of finding symmetry in nature can be seen among animals such as starfish, peacocks, and turtles, and in sunflowers, honeycombs, snowflakes, rainbows, etc.
Symmetry is also commonly used in architecture by architects to build complex designs. A famous example of symmetry in architecture is the Taj Mahal.

You must have seen the following objects in your surroundings:

We can say that the figures show symmetry when the figures are folded in half where we have the left and right halves matching exactly. Hence, the images of these objects show symmetry.
Let us watch this video to know more about symmetry and its applications.
Concepts
The chapter ‘Symmetry’ covers the following concepts:
Symmetrical Figures
We say that a figure shows symmetry when it is folded in half, where we have the left and right halves matching exactly. When you fold symmetric figures into half, one half of the drawing would fit exactly over the other half. Consider the shapes of a door and a pair of spectacles and divide the shape into two halves.

Are the two halves of each shape the same? Yes! Each half of the door is the same as the other half. Also, each half of the spectacles is the same as the other half. Each half is of the same size and shape as the other half. Such shapes are said to be symmetrical.
When you fold them along the dotted line, one half of the drawing would fit exactly over the other half.


If we place a mirror on the dotted line. We see that the image of the one side of the picture will fall exactly on the other side of the picture.

Now look at the following images of objects in your surroundings:



These images can be folded into half but the two halves do not match exactly.

If a figure can be folded or divided into half but the two halves do not match exactly, then such a figure is called an asymmetrical figure.
We can create symmetrical figures using paper cuttings, ink blots, and ink strings. Follow these steps to create symmetrical figures using ink blots:
- Take a piece of paper and fold it in half.
- Spill a few drops of ink on one-half of the side.
- Now press the halves together.
- Unfold the paper, and you will get a symmetric design.
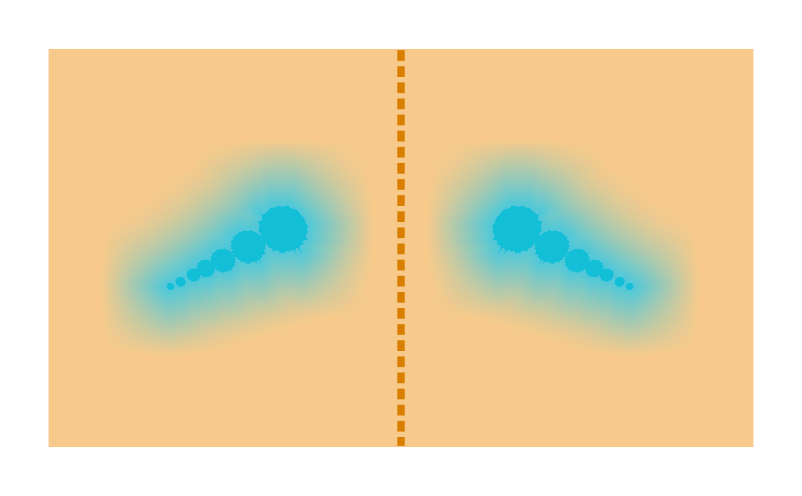
Line of Symmetry
Observe the figures given below:
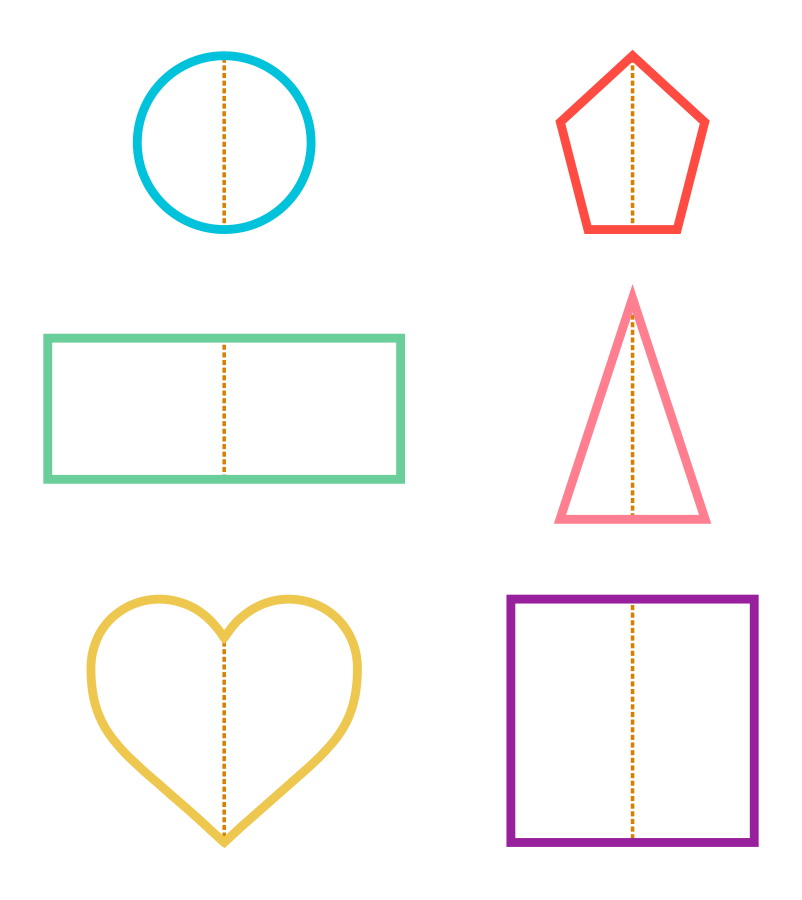
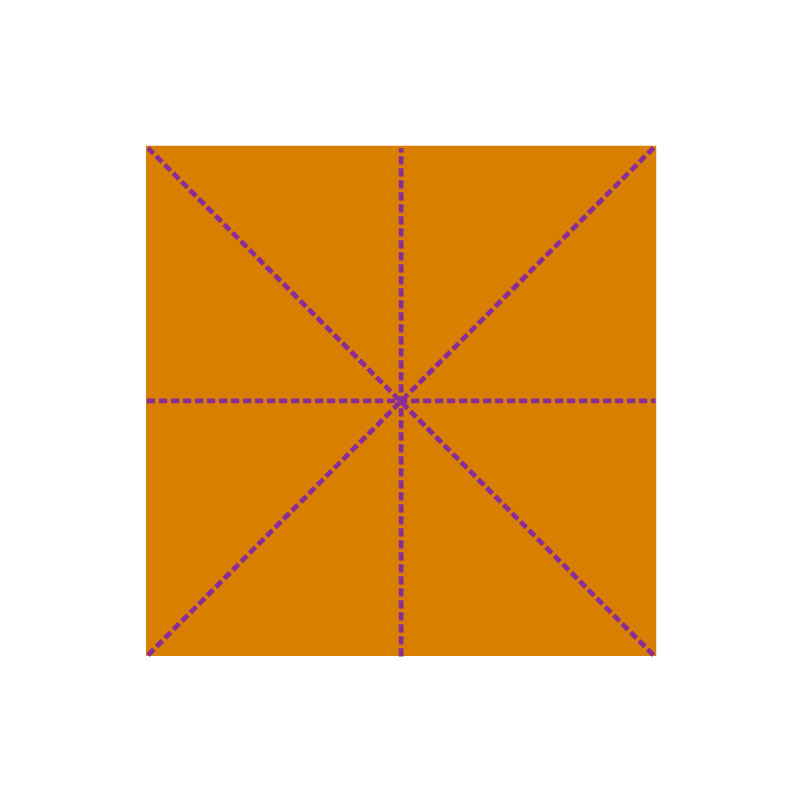
The dotted line, which is the mirror line for a given figure is called the line of symmetry or an axis of symmetry for the figure. The line of symmetry divides the figure into two equal halves. The line of symmetry may be vertical or horizontal or slant. A square has all the three lines of symmetry:
For any symmetrical figure, when we place a mirror along the line of symmetry, the reflection or the mirror image will be the same as the half of the figure. Hence, we can say that about the line of symmetry, one part of the figure is a mirror image of the other
We can visualize and identify the number of lines of symmetry in a given figure by finding the possible number of fold lines that can be created so that the figure is divided into two equal halves. Did you know that some letters in the English alphabet also have lines of symmetry?
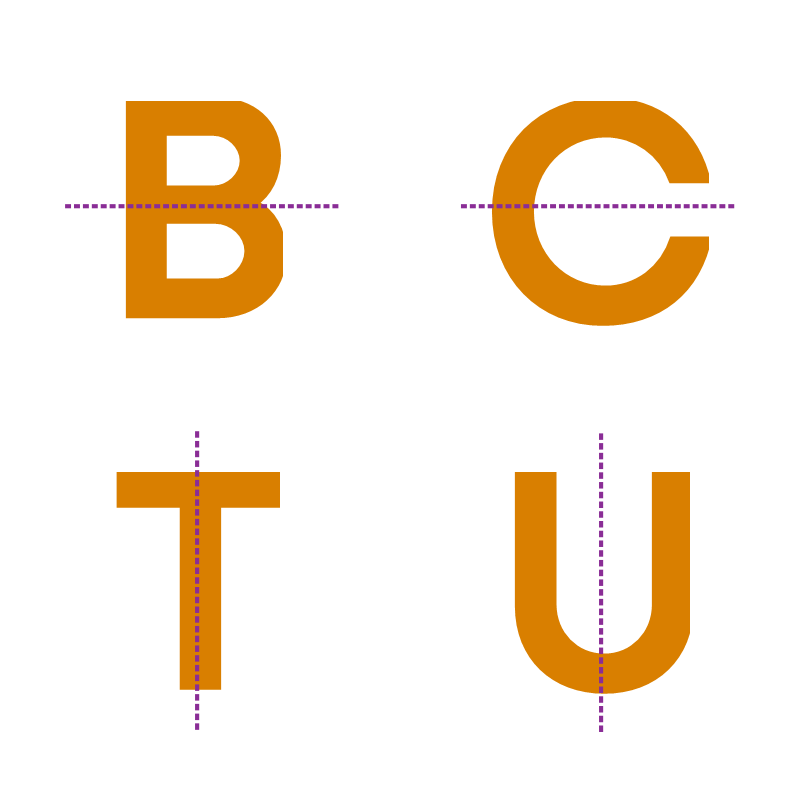
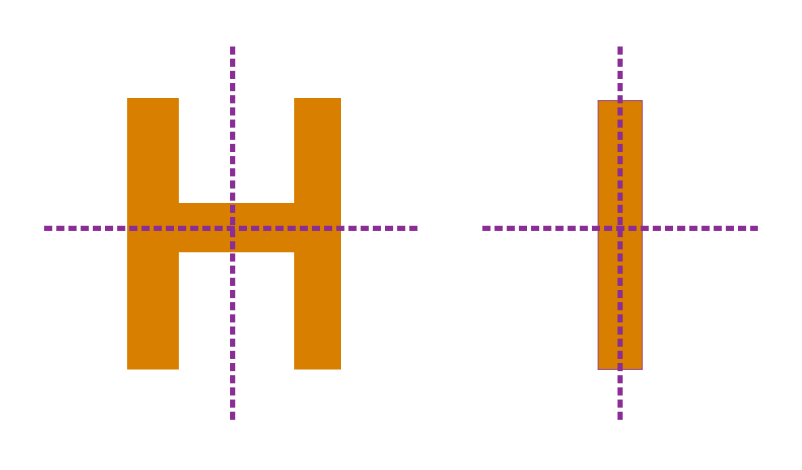
Some letters do not have any lines of symmetry:

Let us learn how to draw a hexagon with exactly two lines of symmetry.
A hexagon has six sides so let us start with drawing two lines
Let us draw two more sides and make the figure symmetric about the vertical line.
Now let us draw two more sides on the lower side of the dotted line.

We draw the remaining two sides such that the hexagon becomes symmetric about the horizontal line.

In this way, we have obtained a hexagon which is symmetric about two lines, hence, having two lines of symmetry.
You can also create symmetric figures using square grids:
We look at each vertex of the image and measure its distance from the fold line.
We draw each vertex corresponding to the image part vertices, keeping the same distance from the fold line.

Reflection Symmetry
When a mirror is placed in the middle of a figure, if the half of the image is the same as its reflection, then it is reflection symmetry.
If we place a mirror on a line such that the image of one side of the figure will fall exactly on the other side of the figure, then this line is called the mirror line.
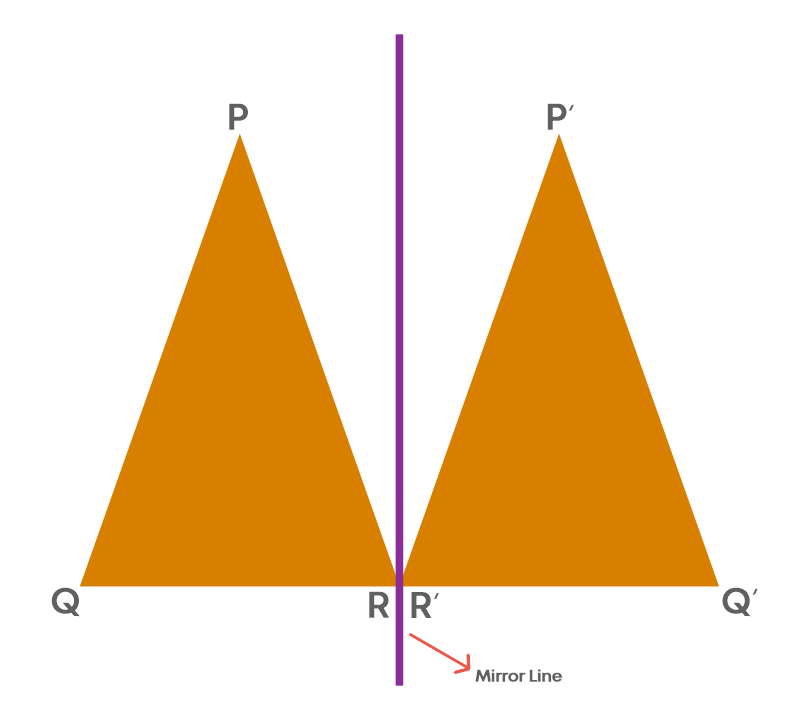
The object and its image are symmetric with reference to the mirror line. When an object is reflected, there is no change in the corresponding lengths and angles of the image.
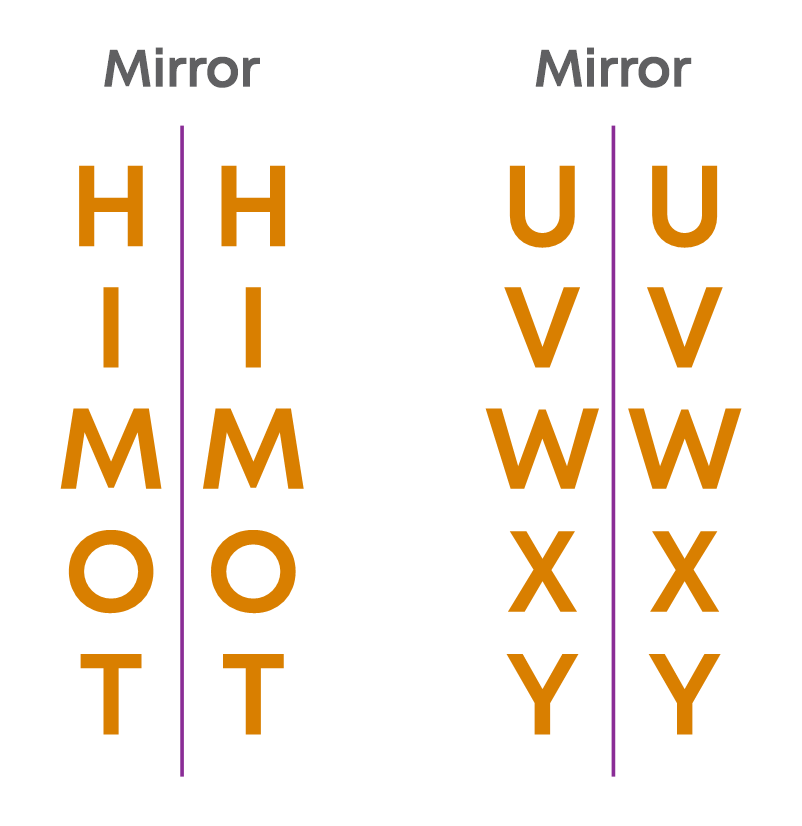
Let us identify the reflection symmetry of different letters.
Hence, the reflection of an object will always be of the same size as the original object.
In reflection symmetry, the left side of the object is changed to the right side in the image and vice versa. The letters T, U, V and A look the same after reflection. The letters Q, P, B, C and Z do not look the same after reflection. Some letters look the same because they have a vertical line of symmetry.
While drawing the mirror image of given objects, we keep in mind the following points:
- We look at each vertex of the image part and measure its distance from the mirror line.
- We draw each vertex corresponding to the image part vertices, keeping the same distance from the mirror line.
Common Errors
The following are the topics in which students make common mistakes when dealing with symmetry:
- 1. A figure can be either symmetric or asymmetric
- 2. Line of symmetry is not always a horizontal line
- 3. Is reflection a type of symmetry?
A Figure Can Be Either Symmetric Or Asymmetric
A figure can be either symmetric or asymmetric but cannot be both. Figures having line/lines of symmetry are symmetric. Figures having no line/lines of symmetry are asymmetric.

Line Of Symmetry Is Not Always A Horizontal Line
The line of symmetry may be vertical or horizontal or slant. The given letter has both vertical and horizontal lines of symmetry.


Is Reflection A Type Of Symmetry?
Reflection is also a type of symmetry. When a mirror is placed in the middle of a figure, if the half of the image is the same as its reflection then it is reflection symmetry. The object and its image are symmetric with reference to the mirror line.

Conclusion
Now you know all about symmetry and its concepts. Can you solve this puzzle?
Which figure should replace the question mark?

Options:
1. 
2.
3.
4.




















































