Introduction
Look around your room or house or classroom. You find different objects and shapes such as the following:

There are many objects around us which are of different shapes. What are these shapes and why do we need to learn about them? Let us watch this video to know:
In this video, we saw that every object around us is made of some basic shape like a line, curve, triangle, circle, etc. To be able to build these objects, we must know more about them.
We should be able to understand what shape suits the object, what should be their size, and how we can create the shapes with the measurements we want. Geometry is also needed to:
- Construct buildings
- Design the furniture for a space
- Make precision tools to cut wood or metal
- Measure area and perimeter of a field or room or a box
- Decide what size and type of packaging is needed for a solid or a liquid
Real-Life Applications Of Shapes:
Have a look at your surroundings, do you notice that even the screen you are looking at now is either a square or a rectangle? Shapes are all around us.
Do you or any of your friends have an interest in arts? Artists often use geometrical elements such as lines, angles, and shapes to create a theme throughout their artwork. World-famous artist Picasso used geometrical shapes throughout his work, which later became his signature style.

Understanding elementary shapes is also useful for scientists and astronomers. The study of geometry starts with single points and branches out to lines and then to three dimensional objects. If you look up at the night sky you will see stars, which are single points.
The arrangement of the stars is such that some stars connect with lines to form basic shapes, which are constellations. Did you know, in ancient times, stars were used to map out the location of places?

Concepts
The chapter ‘Understanding Elementary Shapes’ covers the following concepts:
Lines
A line segment is a geometrical shape which is a part of a line. It has a fixed length and can be measured. It cannot be extended in any direction. Example:
AB is a fixed part of the line ‘m’.

Remember:
We use a ruler to measure the length of a line segment. A ruler has two edges with centimeters on one edge and inches on the other edge. On the centimeter edge, there are a total of 15 equal parts. Each part is of length 1 centimeter or 1 cm.
Each centimeter is divided into 10 smaller divisions.

Each small division is 1 millimeter or 1 mm. Therefore:
1 cm = 10 mm and 1 mm = 0.1 cm
Measuring line segments using a divider is a more accurate method than just a ruler. To measure the length of a line segment using a divider and ruler:
- Open the divider and place the point of the divider on one end point of the line.
- Holding the divider firmly, open the other leg of the divider and place it on the other end point of the line segment.
- Now, take the divider and place it along the edge of the ruler to measure the length.
Now that you know how to measure line segments, let us learn about comparing line segments. Comparing the line segments by mere observation is not an accurate way of comparing. To compare two line segments, we use a divider and a ruler to measure and compare. Measure the length of the first line segment, then measure the second line segment. Now, compare the lengths.
Angles
Let us learn about the different types of angles.
-
A right angle is an angle which is exactly in the shape ‘L’. It also can be considered as an angle made by a line whose turn is 1/4th of a circle or 1/4th of a revolution.

-
An angle which has exactly 2 right angles in it is a straight angle. Example:

Angle DOC or COD is a straight angle. It is made of exactly 2 right angles.
-
An angle which has exactly 4 right angles is a complete or whole angle.

This is a complete angle because after completing one rotation, the line is coming back to its original position.
-
Any angle which is less than a right angle is an acute angle. The angles given below are all acute angles:

-
All angles which are more than a right angle but less than a straight angle are called obtuse angles.

-
A reflex angle is an angle which is more than a straight angle but less than a complete angle.

Every acute, obtuse, and right angle will have a corresponding reflex angle.
Perpendicular Lines
Look around your room or classroom and identify the perpendicular lines.


Such pairs of lines which intersect at right angles are called perpendicular lines. So, two lines are said to be perpendicular lines if the angle made at their point of intersection is a right-angle.
Now, consider a line segment AB with P as its mid-point. Draw a perpendicular to AB through the point P. That is, we will draw MN such that it makes a 90⁰ angle with AB.

Now, MN ⟂ AB. Since, MN is dividing the line segment AB into two equal parts or bisecting the line segment AB, MN is known as the perpendicular bisector of the line segment AB.
Triangles
Triangles can be classified into three types based on the length of their sides:
-
Equilateral triangle: A triangle with all three sides of equal length.

-
Isosceles triangle: A triangle with two sides of equal length.

-
Scalene triangle: A triangle with all three sides unequal in length.

Triangles are also classified based on the measures of their angles.
-
A triangle in which all the three angles are acute angles is an acute-angled triangle.

-
A triangle in which one angle is an obtuse angle is an obtuse-angled triangle.

-
A triangle in which one of the angles is a right angle is a right-angled triangle.

Quadrilaterals
Square
For any square, the following are true:
- All sides are equal.
- Pair of opposite sides are parallel.
- Diagonals are equal.
- Diagonals bisect each other at 90°.
Rectangle
For any rectangle, we can say that:
- Pair of opposite sides are equal in length.
- Pair of opposite sides are parallel.
- All the angles are 90°.
- Diagonals are equal in length.
- Diagonals bisect each other.
- Diagonals are not perpendicular to each other.
A parallelogram is a quadrilateral with each pair of opposite sides parallel and equal. A square and a rectangle are also a parallelogram.
Rhombus
A rhombus is also a parallelogram. Its properties are:
- All sides are equal.
- Diagonals bisect each other perpendicularly.
- Opposite angles are equal.
Trapezium
Properties of a trapezium:
- A quadrilateral with one pair of opposite sides parallel.
- The other pair will be non-parallel.
- No sides are equal in length.
- Diagonals are also not equal.
- The diagonals are not perpendicular to each other.
Kite
A kite is a quadrilateral with:
- Adjacent sides equal.
- One pair of opposite angles equal.
- Diagonals not equal.
- Diagonals perpendicular to each other.
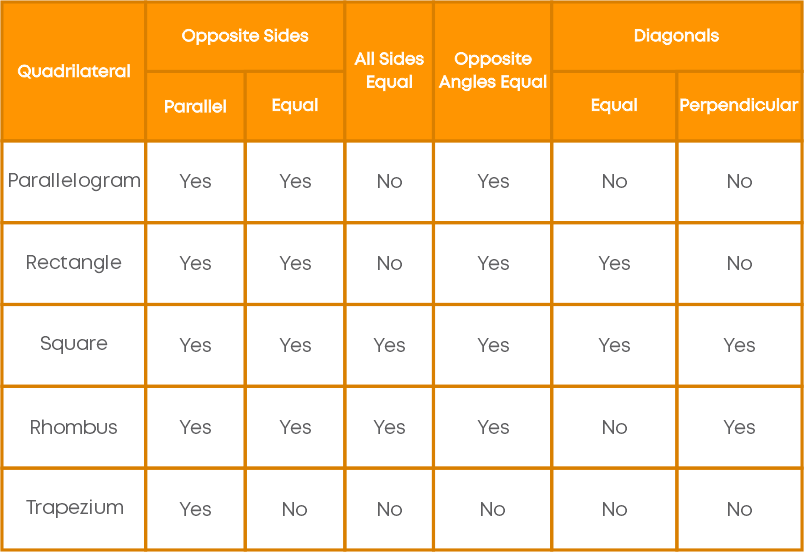
The following table summarises the properties of the sides, angles, and diagonals of different quadrilaterals:
Polygons
Polygons are closed shapes made of only line segments. Polygons can be regular or irregular.
Regular polygons are polygons which have all sides equal and all angles equal. Examples:

Irregular polygons are polygons which have unequal sides or angles. Examples:

Further, based on their angles, polygons can be classified as convex and concave polygons.
-
A convex polygon will have all its angles less than 180°, as shown in figure (a), and a concave polygon will have at least one angle more than 180° or at least one of the diagonals will lie outside the polygon, as shown in figure (b).

3D Shapes
Shapes can further be classified into two types based on their dimensions:
-
2D or two-dimensional shapes: Also known as flat shapes, these shapes have only two dimensions as length and width.

-
3D or three-dimensional shapes: Also known as solid shapes, these shapes have three dimensions as length, width, and height.

There are different 3-dimensional shapes which we see and use every day. 3D shapes can be broadly categorised as:
- Cubes
- Cuboids
- Cones
- Cylinders
- Prisms
- Pyramids
- Spheres
The three main elements of a 3D shape are:
- Faces – The sides of a 3D shape are the faces of the shape.
- Edges – The line where two faces meet is the edge of the shape.
- Vertices – The point where two edges meet is the vertex.
Let us see how many faces, edges, and vertices a triangular prism has.

Common Errors
The following are the topics in which students make common mistakes when dealing with elementary shapes:
- 1. Fraction of revolution covered by the hour hand of a clock
- 2. Measuring angles using a protractor
- 3. Finding the number of faces of a cube / cuboid
Fraction Of Revolution Covered By The Hour Hand Of A Clock
To check what fraction of a revolution is covered when the hour hand of a clock moves from one time to another time. Consider the clock to be divided into 12 equal parts according to the hours.
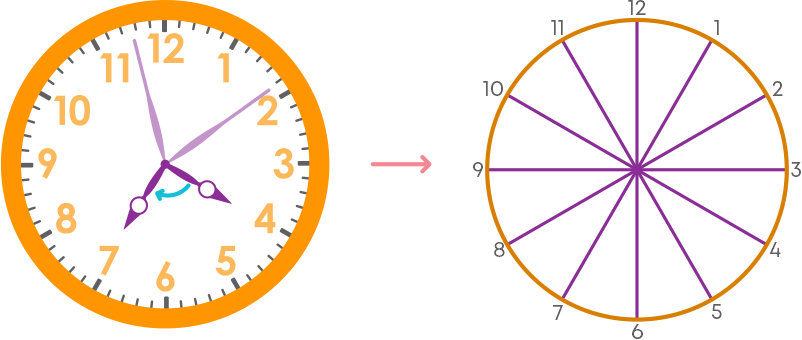
So, the denominator of the fraction will be 12 as the whole is divided into 12 parts. Check the parts covered by the hour hand from the initial time to the end time in the direction that the hand has moved. This will be the numerator of the fraction. Take care of the direction of movement. Example:
Let us say the hour hand moves from 3 o’clock to 8 o’clock in the clockwise direction, so, from 3 to 8, the hour hand covers 5 parts which means the fraction of revolution is 5/12.

Measuring Angles Using A Protractor
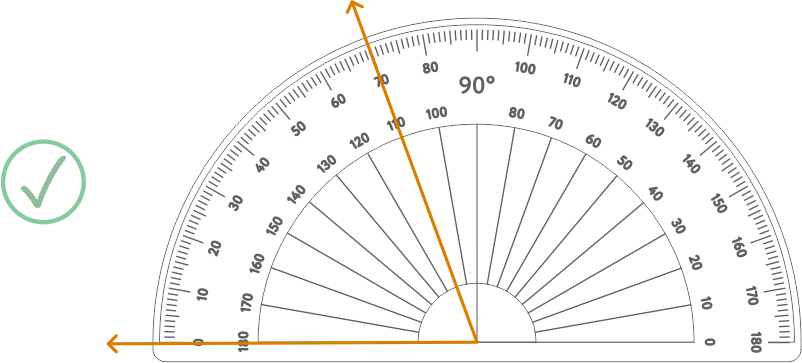
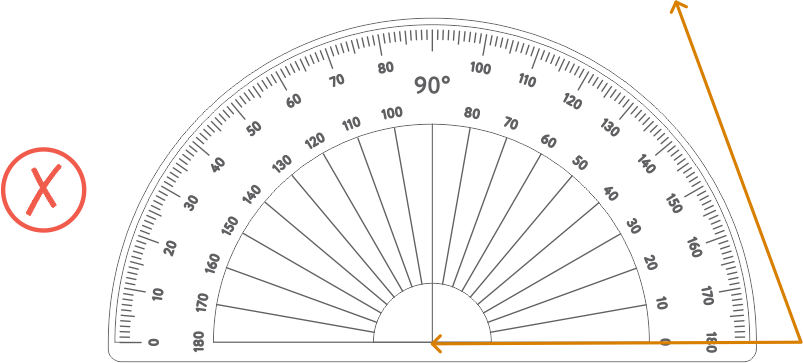
While measuring angles in the anti-clockwise direction using a protractor:
Make sure you place the base line on the base arm of the angle and the origin of the protractor on the vertex of the angle. Since the angle is in the anti-clockwise direction, take care to coincide the 0 on the left side of the protractor on the arm of the angle.
Finding The Number Of Faces Of A Cube / Cuboid
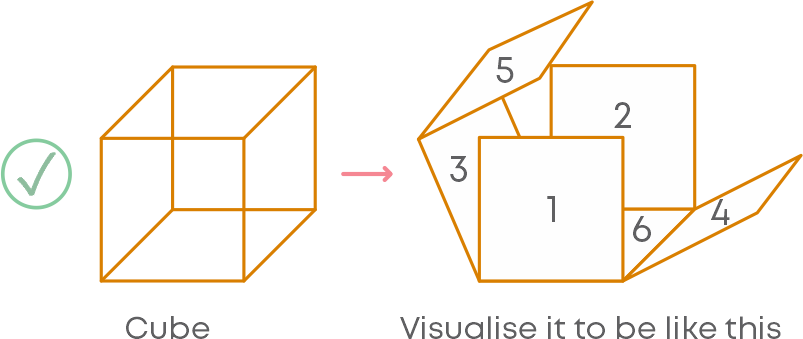
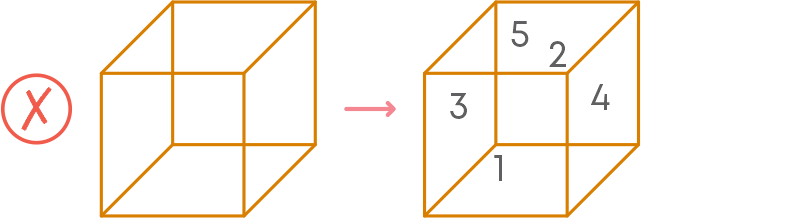
A cube and a cuboid are 3-dimensional shapes. Hence, we must turn them around to see the different sides of the shapes. But on paper, we cannot turn around to see the sides. Instead, we must imagine the sides of these shapes. To find the number of faces of a cube or a cuboid:
Consider:
1 face on the front
1 face opposite to it, i.e., exactly behind the front
2 faces on each side
1 face on the bottom
1 face on the top
So, a cube or a cuboid has 6 faces.
Conclusion
Now you know all about elementary shapes, how to measure them, how to compare them, and their properties. Using this knowledge, can you solve the following riddle?
I have many shapes:
I look square from the outside, circle on the inside, and triangle when taken out.
What am I?




















































