Introduction
Counting numbers from 1, 2, 3.. are called natural numbers. Whole numbers include 0 and counting numbers. Nothing can be written as zero and is represented as “0”.
All counting numbers are natural numbers and they start from 1. All natural numbers are whole numbers. All whole numbers are not natural numbers. Zero is not a natural number but whole number.

Watch the video below to know what whole numbers are:
Now let us examine some real-life applications of the properties of whole numbers:
Reema went to the store and bought a set of 10 pens, but upon reaching home her mother informed her that she already had 4 pens at home.
So, totally, Reema now has 14 pens. Adding two whole numbers will result in a whole number, and the addition is always commutative.
i.e., you can add the two numbers, either way, 10 + 4 or 4 + 10.

The same goes for the multiplication of whole numbers. Reema bought the pens at ₹2 per pen. So, the set of 10 pens she bought will cost (10 × 2 or 2 × 10 =) ₹20.
To find this, you multiply either 10 with 2 or 2 with 10; the answer will be the same and will be a whole number.
Concepts
The chapter ‘Playing With Numbers’ covers the following concepts:
Understanding Whole Numbers
Let us understand the difference between Natural Numbers and Whole Numbers.

Predecessors of Whole Numbers
The predecessor of a number is obtained by subtracting 1 from the given number:

Zero does not have a predecessor. Since whole numbers start from zero, there is no predecessor for zero.
Remember! The predecessor of the largest three -digit number (999) is a three-digit number (998). The predecessor of the smallest three-digit number (100) is a two-digit number (99). The predecessor of the largest four-digit number (9999) is a four-digit number (9998). The predecessor of the smallest 4-digit number (1000) is a 3-digit number (999).
So, the predecessor of a whole number is a whole number which is one step to the left of the whole number. The predecessor of a given number will have the same number of digits as in the given number or one digit less than that of a given number.
Successors of Whole Numbers
Similarly, the successor of a whole number is a whole number which is one step to the right of the whole number. The successor of a whole number is more than the given number. To find the successor of a number, add 1 to the given number.

Remember! The successor of the largest 3-digit number (999) is a 4-digit number (1000). The Successor of the smallest 3-digit number (100) is a 3-digit number (101). The Successor of the largest 4-digit number (9999) is a 5-digit number (10000). The Successor of the smallest 4-digit number (1000) is a 4-digit number (1001).
The successor of a given number will have the same number of digits as in the given number or one more than that of the given number.
When learning about whole numbers, it is important to understand how a number line works. A number line will help you in comparing two numbers.
Can you think of some everyday objects or devices which have a number line on them? Observe below:
A ruler and a thermometer both have straight number lines:

A protractor and a clock have a curved shape, but the number line is no different:

A number line is a horizontal straight line on which whole numbers are arranged from the left to the right. A number line starts from '0' and can be extended to any count of numbers. The numbers are placed at equal intervals. The numbers increase as we move forward, and numbers decrease as we move backwards.
Now, let us understand how to locate numbers on the number line. Let us mark 6 and 13 on the number line.
To form a number line, draw a horizontal straight line, mark the numbers 0, 1, 2, 3… at an equal distance. Then, locate the numbers 6 and 13.

Since 13 > 6, 13 is located to the right of 6. Or we can say that 6 is located to the left of 13.
Number lines are also helpful in conducting addition, subtraction, and multiplication by making ‘jumps’ over the numbers. Let us learn how to perform addition, subtraction, and multiplication using the number line:
Addition

Hence, 2 + 5 = 7.
Subtraction

Hence, 6 - 2 = 4.
Multiplication

Hence, 4 × 2 = 8.
Closure and Commutative Property
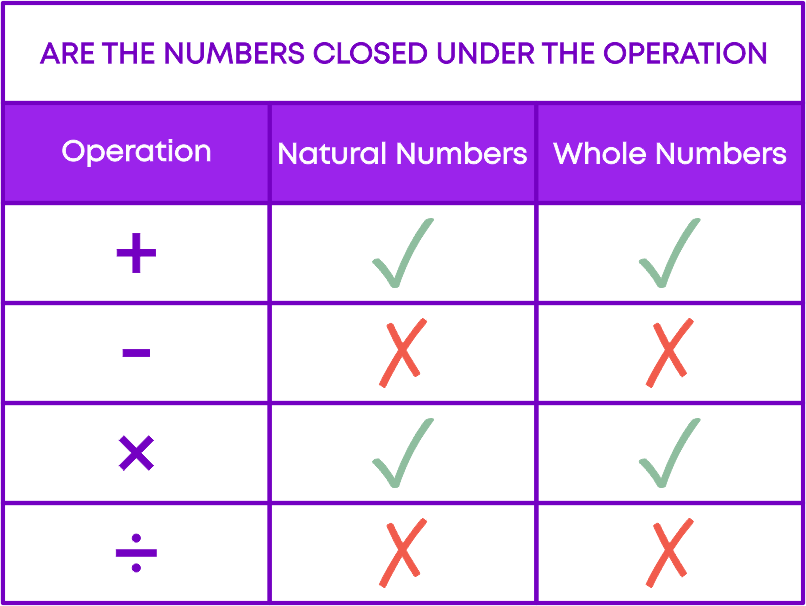
Whole numbers follow closure property under addition and multiplication. The sum/product of two whole numbers is always a whole number.


Therefore, when we add two whole numbers the sum is always a whole number. We can say that whole numbers are closed under addition.
This special property of whole numbers is called the closure property for addition of whole numbers.
Similarly, when we multiply two whole numbers the product is always a whole number. We can say that whole numbers are closed under multiplication.


Whole numbers do not follow closure property under subtraction or division.
The difference of two whole numbers is not always a whole number. Observe the following subtractions.

The result of the division of two whole numbers is not always a whole number. Observe the following division:

Let us now understand closure property of natural numbers and whole numbers under different operations:
Whole numbers follow commutative property under addition and multiplication. Two whole numbers can be added/multiplied in any order.
That is:
-
if ‘a’ and ‘b’ are two whole numbers then, a + b = b + a

- if ‘a’ and ‘b’ are two whole numbers then, a + b = b + a

Remember, whole numbers are not commutative under division and subtraction.

Consider subtracting 9 and 5 in two ways:
9 – 5:

5 – 9:

From the above, we can say that the subtraction and division of whole numbers is not commutative.
Associative Property
Whole numbers follow closure property under addition and multiplication. The sum/product of two whole numbers is always a whole number.
Whole numbers follow associative property under addition and multiplication. To add/multiply three numbers, any two numbers can be grouped and added/multiplied first. The sum/product remains the same even when the grouping is changed. That is:
-
if ‘a’, ‘b’ and ‘c’ are three whole numbers then, (a + b) + c = a + (b + c)

-
if ‘a’, ‘b’ and ‘c’ are three whole numbers then, (a × b) × c = a × (b × c)

Whole numbers do not follow associative property under subtraction and division.


Associative property lets you re-arrange the numbers in numeric expressions for easier calculations. Identify the numbers which can be multiplied easily. For example, the numbers whose sum or product will be a multiple of 10, 100, etc. Group these numbers and simplify the numeric expression.
Remember: when we apply associative property, we cannot randomly group numbers. We need to group friendly numbers.
Distributive Property
Whole numbers also follow distributive property of multiplication over addition. That is, if ‘a’, ‘b’ and ‘c’ are three whole numbers then,
a × (b + c) = (a × b) + (a × c)

We use distributive property to solve numeric expressions.
Split the number in the expression as a sum of two numbers, e.g., 6 × 102 can be written as 6 × (100 + 2).
Identify the common number in the given expression to form a sum of two numbers, e.g., 12 × 7 + 12 × 3 = 12 × (7 + 3).
Properties of 0 and 1
Did you know? Zero is the additive identity of whole numbers. For any whole number ‘a’, a + 0 = a.
One is called an identity for multiplication of whole numbers or the multiplicative identity of whole numbers. For any whole number ‘a’, a × 1 = a.
Now, the product of any whole number and zero is ‘zero’. In general, for any whole number ‘a’, a × 0 = 0.
Patterns in Whole Numbers
Did you know that we can derive relationships between the whole numbers by finding patterns between them? Let us start representing each whole number with a set of dots and arrange these dots in some geometrical shapes to find number patterns. To arrange these dots, we can take four shapes:
-
Line
The number 3 can be represented by

-
Rectangle
The number 6 can be arranged as a rectangle with 2 rows and 3 columns as

-
Square
The number 4 can be represented as

-
Triangle
The number 3 can be represented as

Number patterns are a sequence of numbers that are ordered based upon a rule. For example:
- The numbers 2, 4, 6, 8, … are a set of even numbers.
- The numbers 10, 20, 30, 40, ... are multiples of 10.
By observing the numbers, we can identify the relationship among them and find out the next number that occurs in the pattern. There are many ways to figure out the rule, such as:
- Use a number line to see the distance between the numbers or what they have in common.
- Look at the last one or two digits or the first digit to see if they repeat in a particular manner.
- Look at the numbers and see if there is a pattern, like taking each number and multiplying.
- Think about the common number patterns, like counting by 2’s, 5’s or 10’s.
- Find the difference between the numbers.
We can use number patterns to simplify numeric expressions involving addition, subtraction, multiplication, etc. Observe the given pattern, identify the rule, and apply the same rule to find out the next step. Consider the product of 84 and 9:
84 × 9
= 84 × (10 – 1)
= 840 – 84
= 756
Hence, 84 × 9 = 756.
Common Errors
The following are the topics in which students make common mistakes when dealing with whole numbers:
- 1. Group friendly numbers
- 2. Distributive property of addition over multiplication
- 3. Properties of zero
- 4. Successor of a whole number
- 5. Predecessor of a whole number
Group Friendly Numbers
When you apply associative property, we cannot randomly group numbers. We need to group-friendly numbers. For e.g., 67 + 245 + 13 should be ideally grouped as
(67 + 13) + 245, as 67 + 13 gives 70.
(We call 67 and 13 as friendly numbers as their sum is a multiple of 10, 100, etc.)
Distributive Property Of Addition Over Multiplication
For any three whole numbers a, b and c,

Properties Of Zero
Remember properties of zero.
- Zero added to any number is the number itself.
0 + 5 = 5 - Zero multiplied by any number is 0.
0 × 5 = 5
Successor Of A Whole Number
The successor of a whole number is a whole number which is one step to the right of a whole number. What is the successor of 3? Is it 2 or 4? Let us find the successor of a whole number 3. Now, if we move 1 step to the right of 3, we get the successor of 3.

Hence, the successor of whole number 3 is 4.
Predecessor Of A Whole Number
The predecessor of a whole number is a whole number which is one step to the left of a whole number. What is the predecessor of 2? Is it 1 or 3? Let us find the predecessor of a whole number 2. Now, if we move 1 step to the left of 2, we get the predecessor of 2.

Hence, the predecessor of whole number 2 is 1.
Conclusion
Now you know whole numbers and their properties. Can you solve this riddle?
Solve for the question mark:





















































