Introduction
There are many shapes around us. You have learnt about plane shapes and solid shapes in your earlier classes. Let us visualise solid shapes in this blog.
You must have seen these objects around you:

Observe that these objects have length, breadth, and height.

So, they all occupy space and have three dimensions. Hence, they are called three-dimensional shapes or 3D shapes or solid shapes.
Concepts
The chapter ‘visualising solid shapes’ covers the following concepts:
Views of 3D Shapes
You have come across 2-D shapes and 3-D shapes. Now, let us look at some examples of combinations of shapes around us. We can recognise different shapes of nested objects. Nested objects are the objects that are inside another object.
Raj bought an ice cream.

Look at the shape of this ice cream.

Is it a combination of 2 shapes? Yes! This ice – cream is a combination of a cone and a hemisphere.

Now, let look at another example. Observe the figure given below.

Here, this is made up of a cylinder and two hemispheres.

Like these, we can find many figures which are combinations of shapes. Shapes can be a combination of the same solid shape or different solid shapes.
The different views of objects are top view, front view, and side view. Example: different views of a car.

- The view from the front is the front view
- The view from the side is the side view
- The view from the top is the top view
Example: different views of a house:

Now, consider a solid shape.
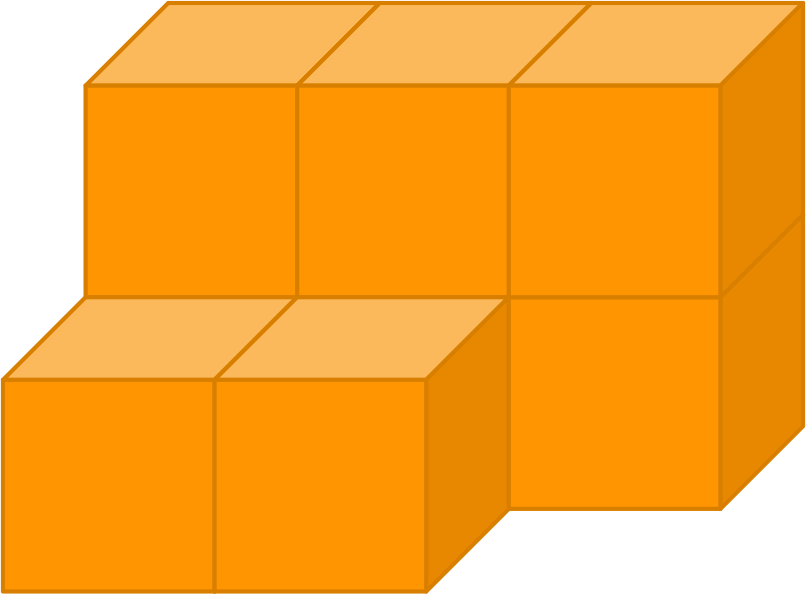
The front view, top view and side view of the given solid are as follows:

Another example:
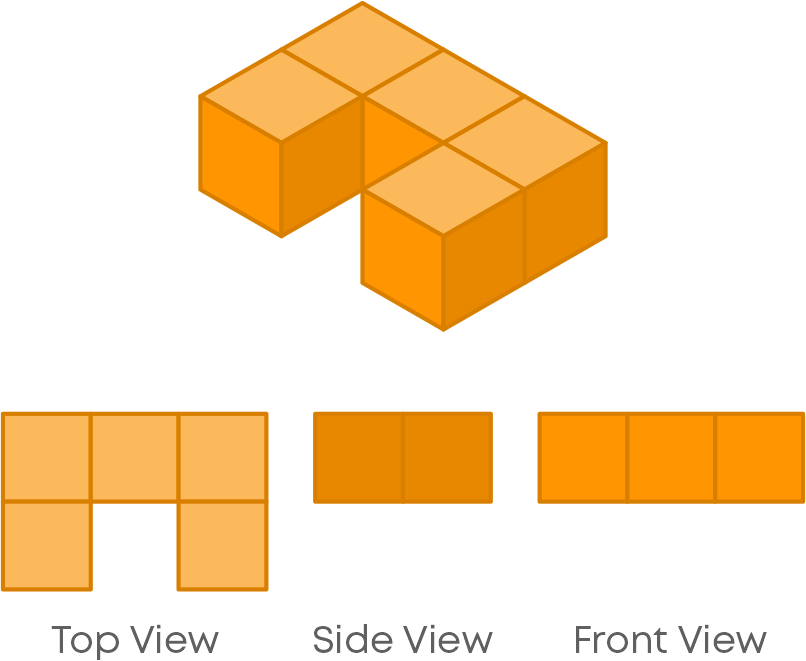
So, solid shapes also have different views from different positions
Faces, Edges, And Vertices
Shapes such as a cone, sphere, and cylinder are not made up of only line segments. Let us look at the sphere.
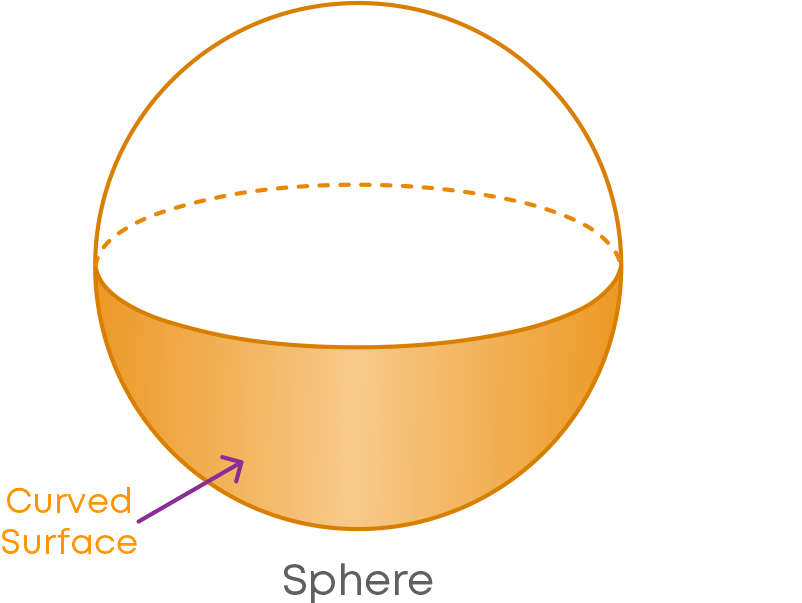
From this, we can see that sphere is a solid which has a curved surface.
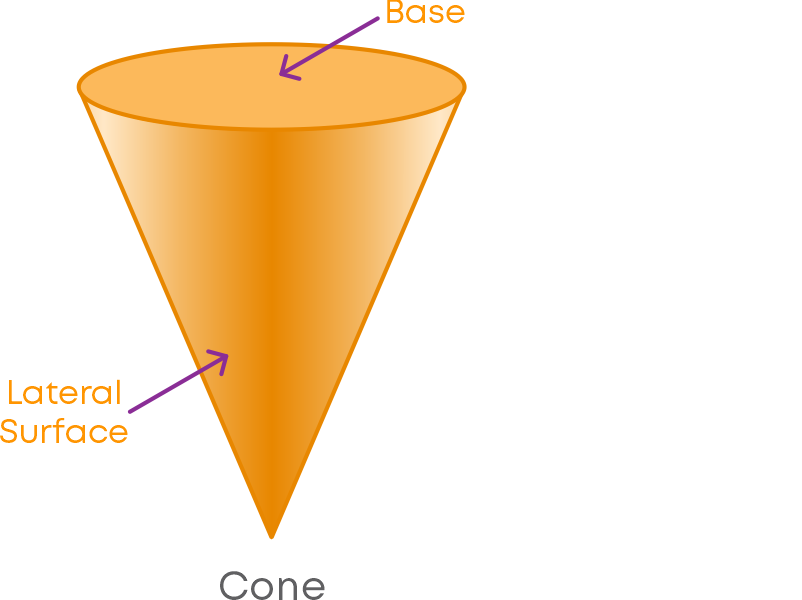
Cone is a solid which has a base and a lateral surface.

Similarly, a cylinder also has a circular base and a lateral surface which is curved as shown in the figure. Now, let us look at different shapes.

How do you differentiate these shapes and the shapes which we discussed above?

We can clearly see that the shapes which are on the right side of the table are shapes whose faces are polygons. Do all these shapes have faces, vertices, and edges?
Yes, each of these solids is made up of polygonal regions which are called its faces. These faces meet at edges which are line segments. The edges meet at vertices which are points. Such solids are called polyhedrons.
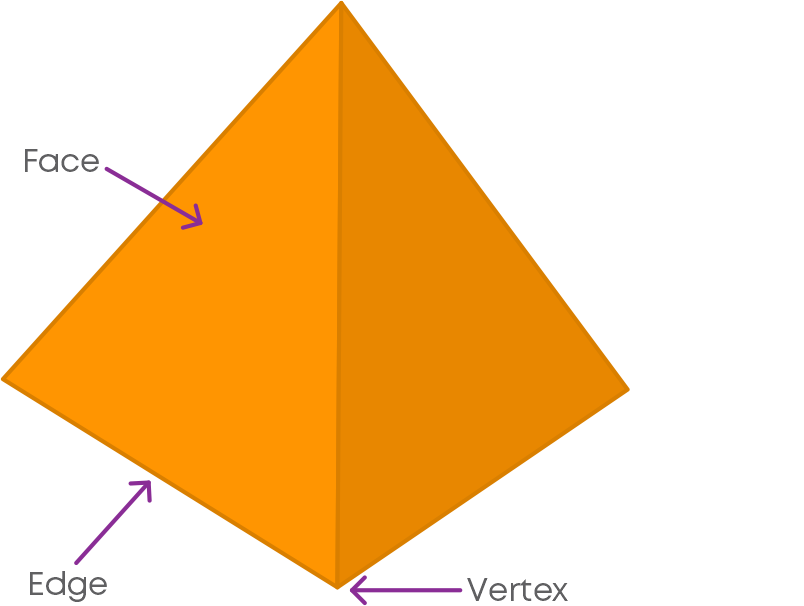
In other words, polyhedrons are three-dimensional shapes with polygonal faces.
A polyhedron is a geometric solid in three dimensions with flat faces and straight edges, i.e., each face is a polygon. Examples of polyhedrons:

The following image will help you remember how to differentiate between a polyhedron and a non – polyhedron:

In convex polygons,
- All the interior angles are less than 180°
- No diagonal has its portion lying on the exterior of the polygon
- Any line segment joining two different points in the interior of the polygon lies wholly in the interior of the polygon.
Now, let us learn about convex polyhedrons. Consider a polyhedron as a cube.

Consider two points in the interior of the polyhedron and join the points with a line segment.

Here, we can see that the line segment joining the two different points in the interior of the polygon lies wholly in the interior of the polyhedron. Also, all the faces of the polyhedron are convex polygons. We call these type of polyhedrons as “convex polyhedrons.”
Now, let us consider a polyhedron and take the two points in the interior surface of the polyhedron and join the points with a line segment.

Here, we can see that a portion of the line segment joining the two points lies in the exterior of the polyhedron. We call these type of polyhedrons as “non - convex polyhedrons”.
Now, let us see some examples of regular polyhedrons.
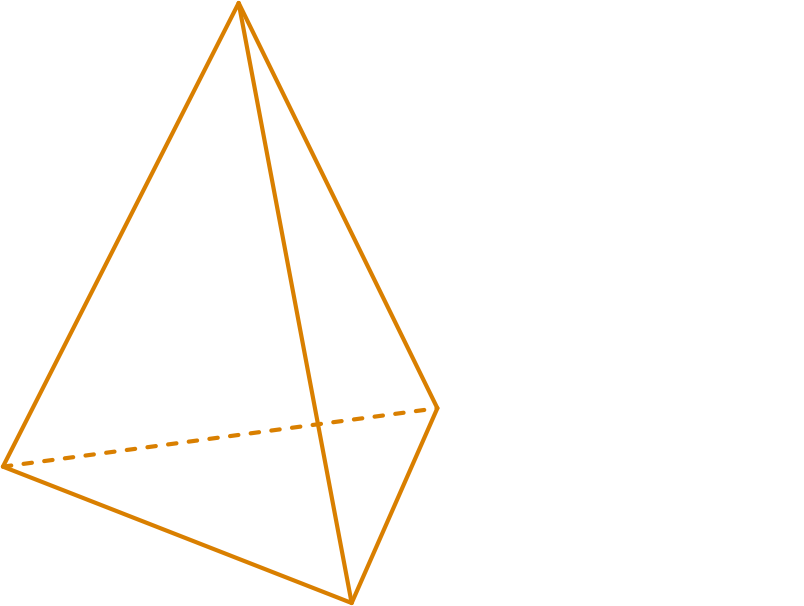
Here, we can see that the faces of polyhedron are formed by regular polygons and the vertices are formed by the same number of faces.
A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex.
Let us look at an example of an irregular polyhedron.
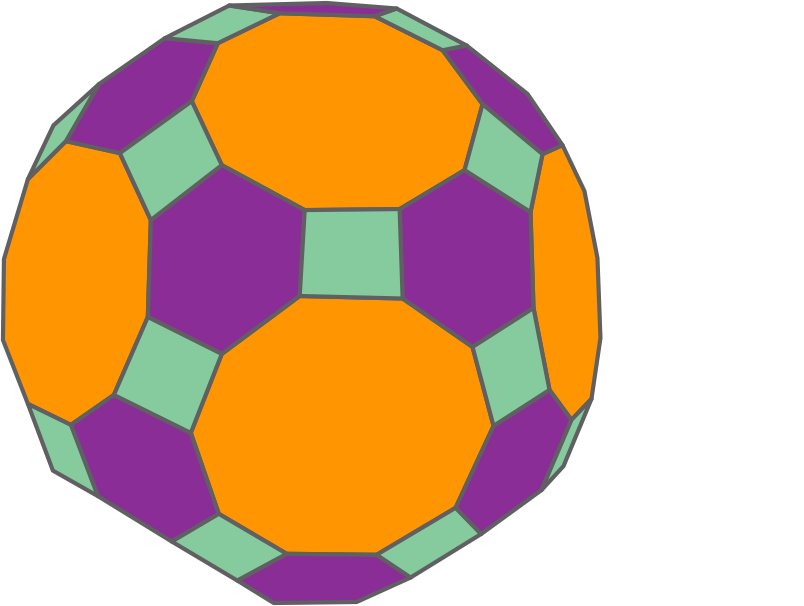
Here, we can see that the faces are made up of irregular polygons and the number of faces that meet at each vertex is different. So, it is an irregular polyhedron.
A polyhedron is said to be irregular if its faces are made up of irregular polygons and the different number of faces meet at vertices.
We have already learnt about the two polyhedrons shown below.
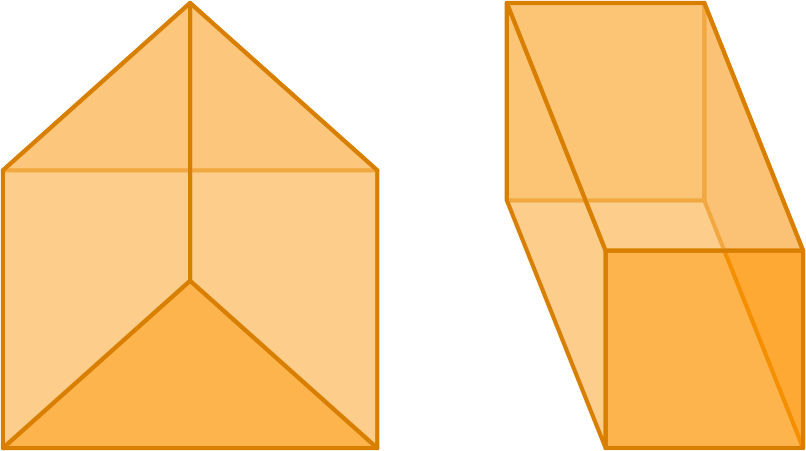
Also, we noted that two things are common about these polyhedrons.
- The lateral faces are parallelograms.
- Base and top are congruent polygons.
We call such polyhedrons as prisms. Also, we name the prism according to its base. For example,
If the prism has a triangular-shaped base, then we call it as a triangular prism.

If the prism has a square-shaped base, then we call it as a square prism.
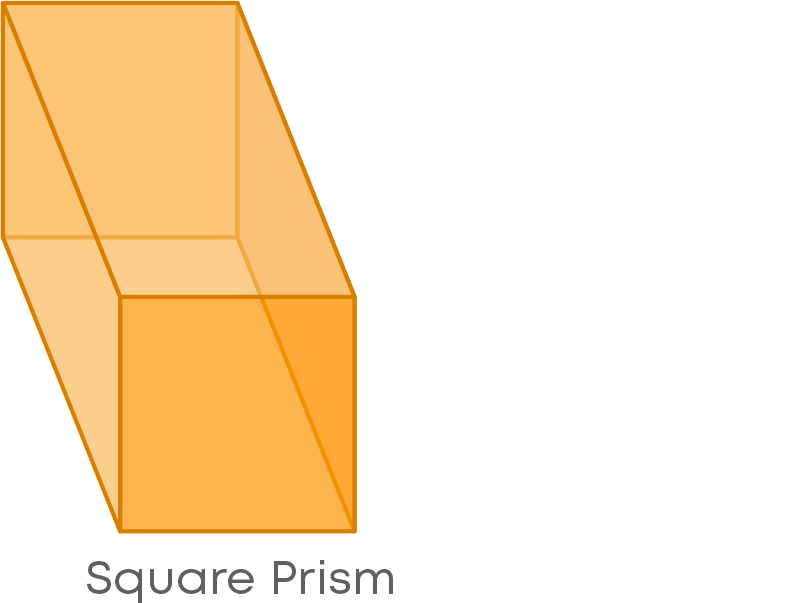
A polyhedron whose base is a polygon and lateral faces are triangles with a common vertex. We call such polyhedrons as pyramids. Let us look at one example of a pyramid.

We can see that here the base of the polyhedron is a triangle, and the lateral faces are triangles with a common vertex. So, it is a pyramid. Also, we name the pyramid according to its base. For example,
If the pyramid has a triangular-shaped base, then we call it a triangular pyramid.

If the pyramid has a square-shaped base, then we call it a square pyramid.

Euler’s Formula:
For any polyhedron, F + V = E + 2
Where V stands for number of vertices, F stands for number of faces, and E stands for number of edges.
This is known as Euler’s formula. If Euler’s formula doesn’t apply for the given vertices, faces and edges, then they do not form a polyhedron.
Consider a cuboid.

First, let us see how many faces, vertices and edges it has.
Faces = F = 6
Vertices = V = 8
Edges = E = 12
Now, let us apply Euler’s formula, F + V = E + 2
F + V = 6 + 8 = 14
E + 2 = 12 + 2 = 14
Hence, Euler’s formula is verified.
Consider this example:
A polyhedron has 5 faces and 9 edges. Find the number of vertices of the polyhedron.
Given that, a polyhedron has 5 faces and 9 edges, i.e., F = 5, E = 9
Let us apply Euler’s formula to find the number of vertices. We know, F + V = E + 2
5 + V = 9 + 2
5 + V = 11
So, V = 11 – 5 = 6
Hence, the number of vertices of the polyhedron is 6.
Mapping Space Around Us
You have learnt that a 3-dimensional object can look differently from different positions. We can draw each side of the object to show how it looks from different perspectives. Here, the top view of a house (from the roof) is given.
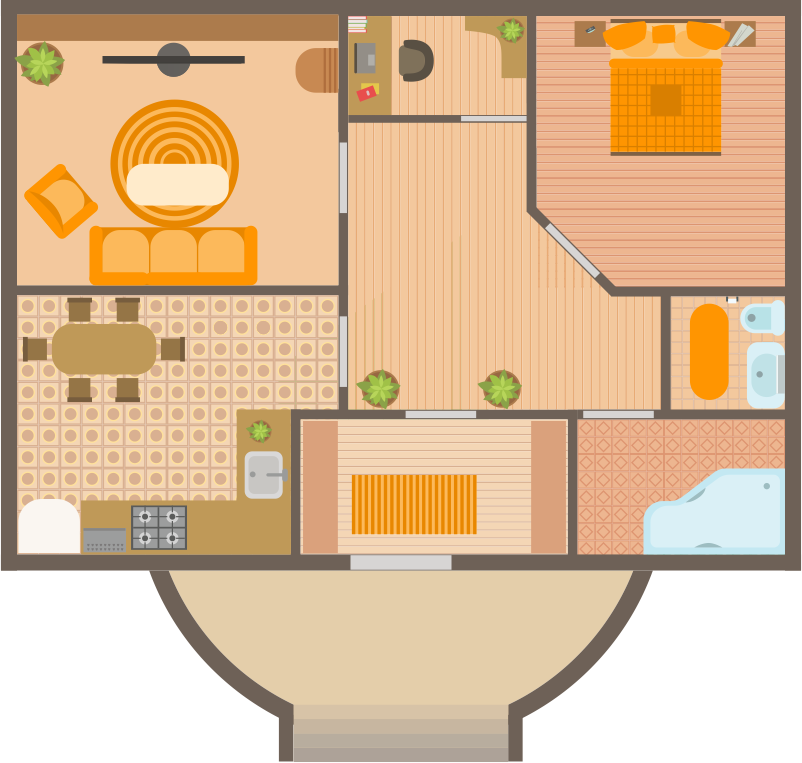
Have you seen these kinds of pictures anywhere? When somebody is planning to buy a new flat, these kinds of pictures of the house will be provided by the property owner. This is the plan of the house. It shows the relative positions of the rooms, or the space used for each room of the house.
Here, every object that can be kept in the house is represented using small pictures, every room is represented using rectangles, etc. This is called the map of the house. You would have seen the maps of cities, states, and countries.
A map basically shows the relation between a particular object or place with other objects/places. Symbols are used to show different objects or places. Maps use a scale which is fixed for a particular map. The scale can vary from map to map.
Consider this example where a girl has drawn a map of the route between her school and house.
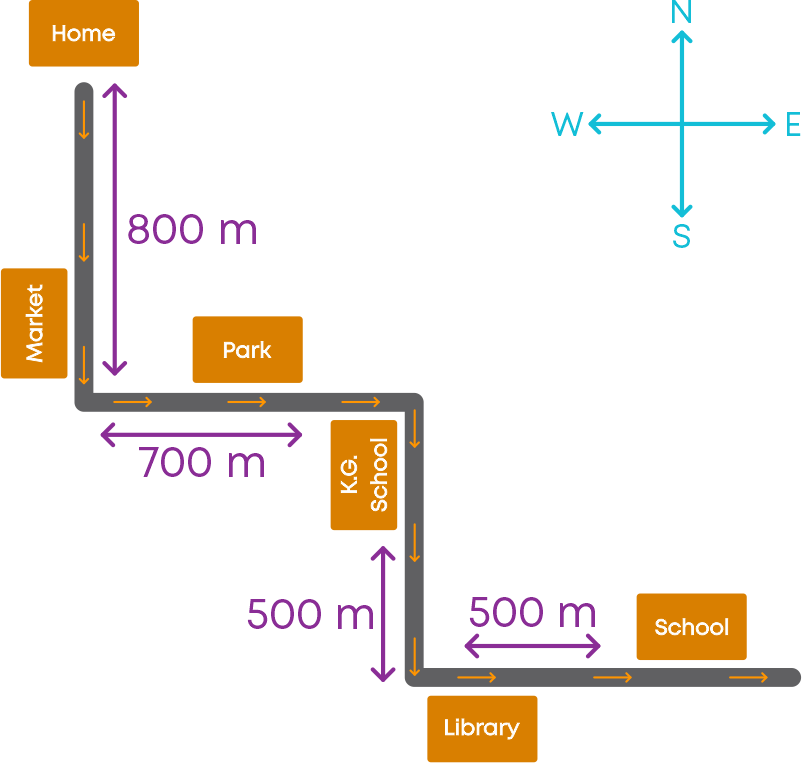
It gives a clear picture of the route between her house and school. Looking at this map, one can have an idea of:
- Different landmarks in the route
- The distance between them
- he total distance between the house and the school
Observe that the distances shown on the map are proportional to the actual distances on the ground. This is done by considering a proper scale. While drawing (or reading) a map, one must know, to what scale it must be drawn (or has been drawn). That is, how much of the actual distance is denoted by 1 mm or 1 cm in the map. This scale can vary from map to map but not within a map.
So, the scale of a map says how much of the actual distance is denoted by 1 mm or 1 cm in the map.
We know that a map of a route or a city gives its clear picture. Here is a map of the route between Aditi’s home and her school.
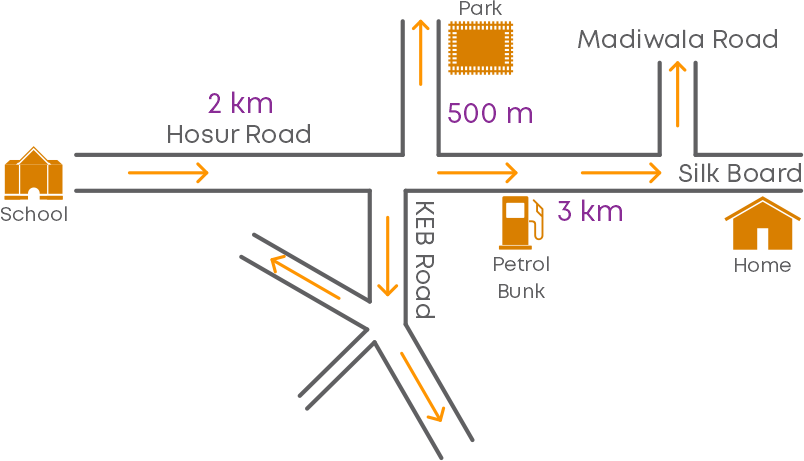
Observing this map, can you describe the route between the school and the home? Can you say which one is nearer to the park, the home or the school?
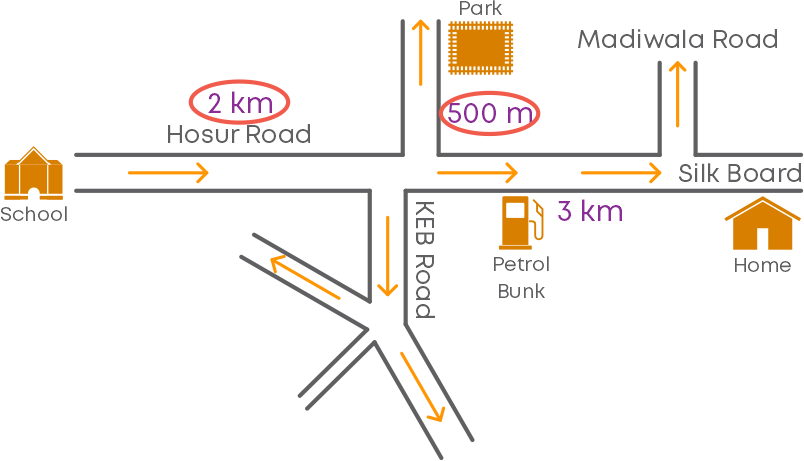
We can see that the distance between the school and the park is given by 2 km + 500 m,
i.e., the distance between them is 2.5 km.
The distance between the home and the park is given by 3 km + 500 m,
i.e., the distance between them is 3.5 km.
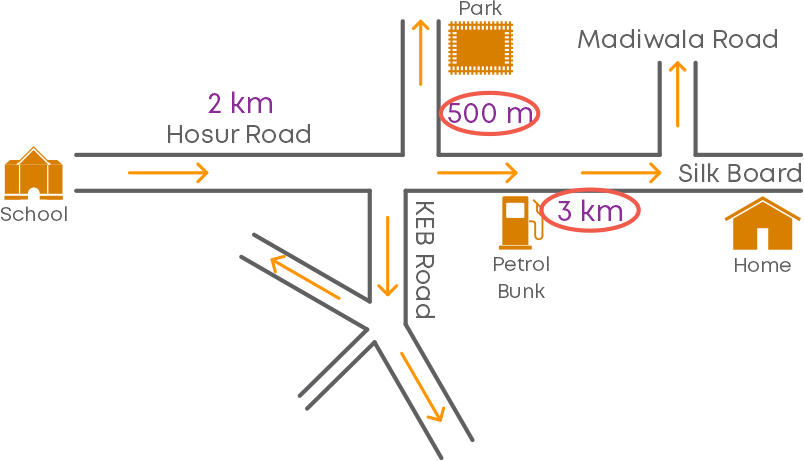
So, which place is nearer to the park? The school is nearer to the park.
What is the distance between the school and the home? The distance between the home and the school is given by 2 km + 3 km,
i.e., the distance between them is 5 km.
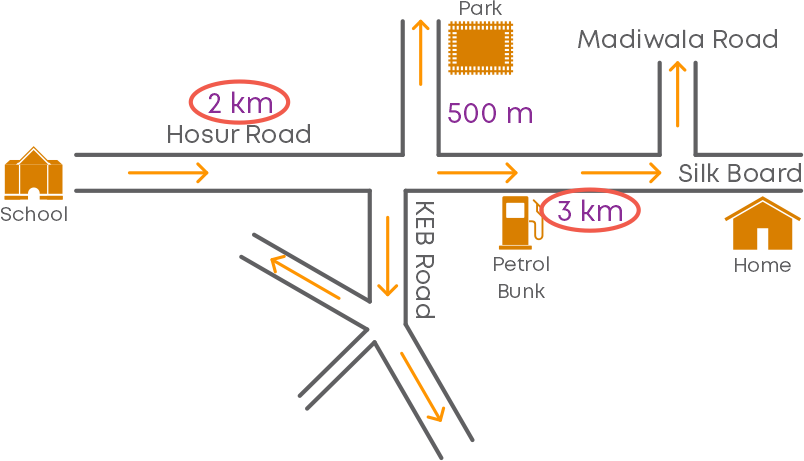
Is there any landmark on the route between the home and the school? We can find that there is a petrol bunk on the route.
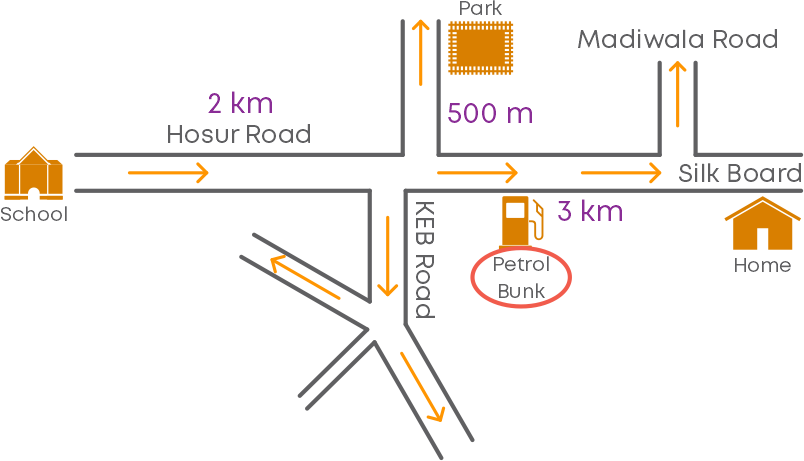
Thus, we can interpret a map with the information represented in it.
Observe the map of a place given below.
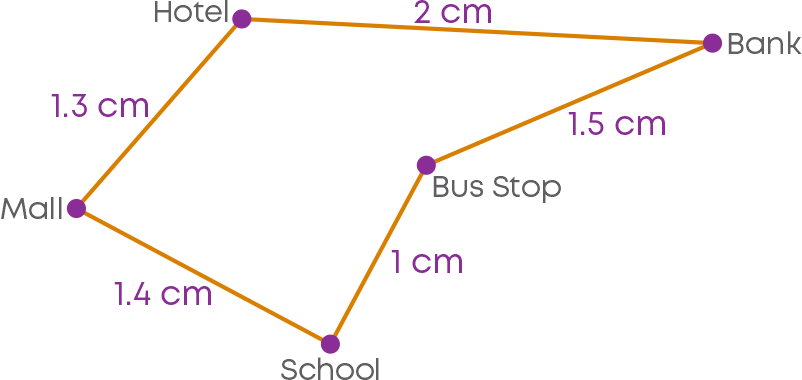
In the map, the distance between the places is shown in 'cm'. A distance of 200 m is represented with a length of 1 cm in the map. This means the distance is shown using the scale 1 cm : 200 m.
What is the length of the line segment joining the points representing the bus stop and the school? It is 1 cm.
Then, what is the actual distance between the school and the bus stop? We know that a distance of 200 m is represented with a length of 1 cm in the map. So, the actual distance between the school and the bus stop is 200 m. Every 200 m is represented as 1 cm. So, the actual distance between the two places will be calculated proportionately.
If the distance between two places is mentioned in smaller units (mostly in centimetres) and the scale of the map is given, then the actual distance is calculated using the concept of ratio and proportion.
A survey on the businesses running around a school is represented as shown below.
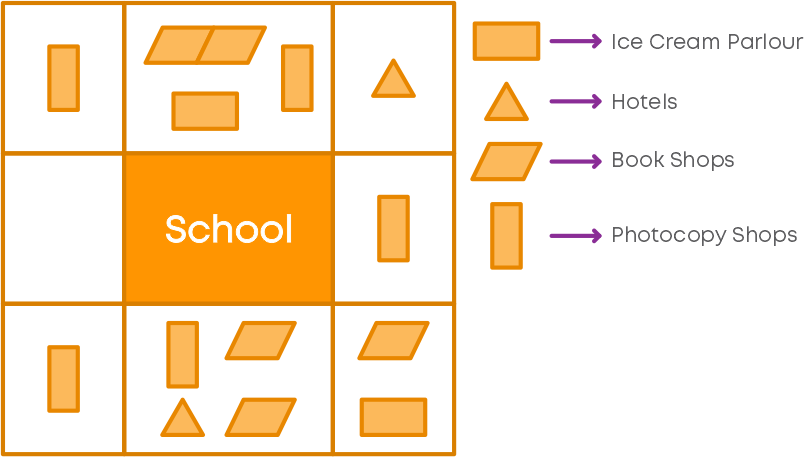
By observing this map, can you say on which businesses the survey was conducted?
We can observe here that ice cream parlours, hotels, book shops and xerox shops are represented using different symbols. So, the survey was conducted on these businesses.
Can you find what is the number of book shops running around the school? First, look for the symbol which represents book shops.
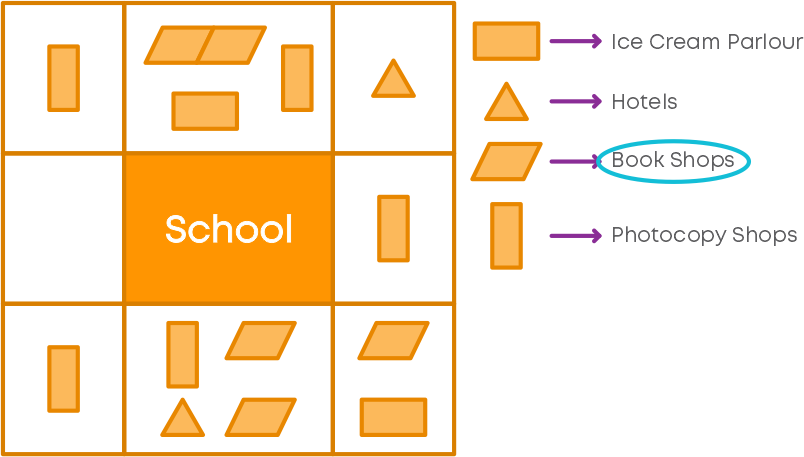
We can find that book shops are represented using parallelograms. How many parallelograms do you find in the map?
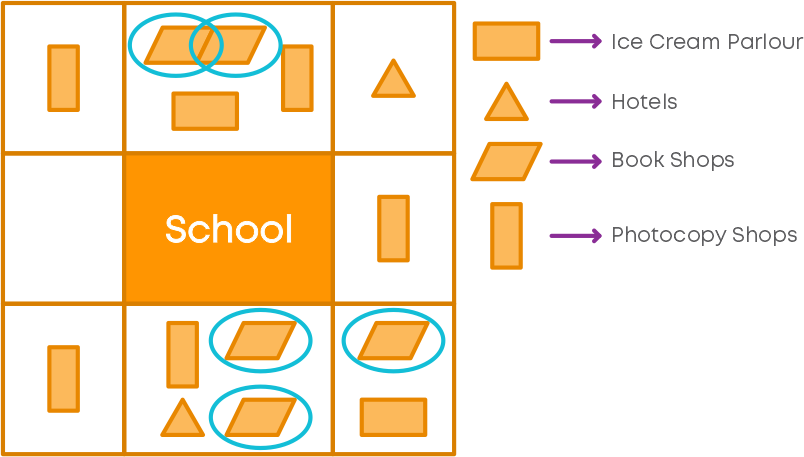
We observe that there are 5 parallelograms. So, we can say that there are 5 book shops around the school.
Common Errors
The following are topics in which students make common mistakes when dealing with visualising solid shapes:
- 1. Finding the actual distance between two places when the scale is given.
- 2. Identifying polyhedrons
Finding The Actual Distance Between Two Places When The Scale Is Given
To find the actual distance between two places when the scale is given, we need to convert the given distance in a map according to the given respective scale. For example, here the scale of the map is given as 1 cm : 100 m.
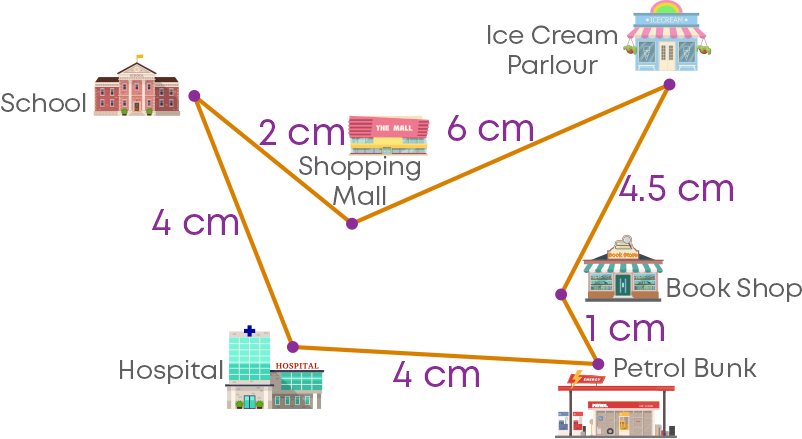
To find the distance between the hospital and the petrol bunk, we cannot directly say that the actual distance is 4 cm. We cannot represent the actual distance in a map since it is a larger unit. So, we need to convert the distance to 4 cm according to the given respective scale.
The actual distance can be found as follows:
A distance of 100 m is represented with a length of 1 cm on the map. The distance between the petrol bunk and the hospital is represented as 4 cm. So, if we consider the actual distance to be ‘x’ m, then we have
1: 4::100 : x
⇒ x = 100 × 4
= 400
Therefore, the actual distance between the petrol bunk and the hospital is 400 m = 0.4 km.

Identifying Polyhedrons
While identifying polyhedrons, we need to observe the following:
Check whether the given 3D shape is made up of flat faces and straight edges or not. For example, sphere, cone, and cylinder are not polyhedrons while cubes, pyramids, and prisms are polyhedrons.

Conclusion
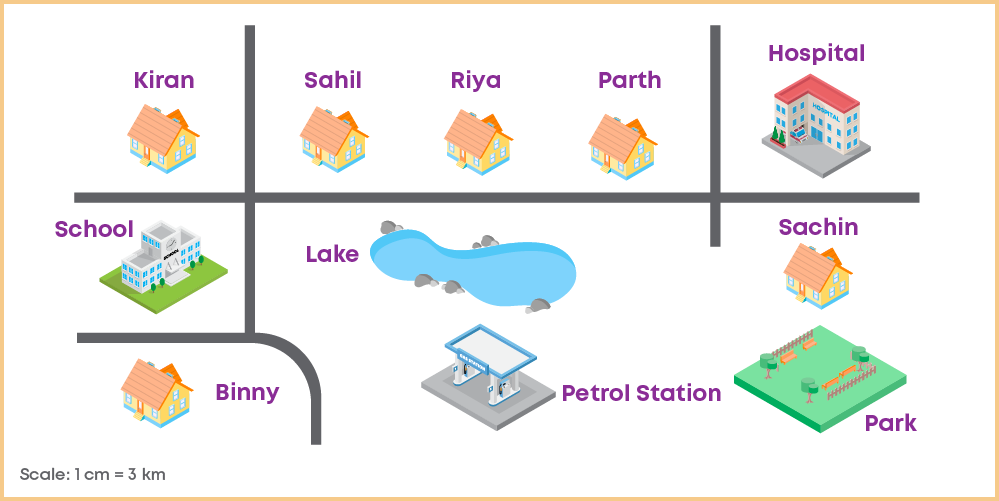
Solid shapes are all around us. Can you solve this riddle based on everything you learnt in this blog about maps?
Below is a map of the locality where Sachin stays.
Complete the following statements based on the map and the scale given.
(a) If the distance between Sachin’s house and the school is 6.2 cm on the map, the actual distance is _____ km.
(b) If the actual distance between the hospital and the petrol station is 12.9 km, the distance on the map will be _____ .
(c) The distance between Binny’s house and the park is 3 cm while the distance between Riya’s house and the park is 4 cm.
The ratio of the distances between Binny to Riya’s house will be _____ .