Introduction
We have learnt about different shapes. Let us watch this video to know these shapes and what we call them.
Have you observed the shape of the door of your classroom?

Notice that the sides or edges of the door are all straight lines. You would have seen more such objects around you. A few are shown below.


Each of these shapes are made by line segments. To use these shapes in buildings or other real-life constructions, it is important for us to know
- what these shapes are
- what their properties are
- what their measurements should be
We know that many of the objects we use in real-life are four-sided shapes. The sides of each of these were line segments. Such shapes are called quadrilaterals.
A quadrilateral is a geometric shape which is closed and made up of four line segments which are called its sides.
To construct these, it is important to know more about the properties of these shapes.
Concepts
The chapter ‘Understanding Quadrilaterals’ covers the following concepts:
Revisiting Polygons
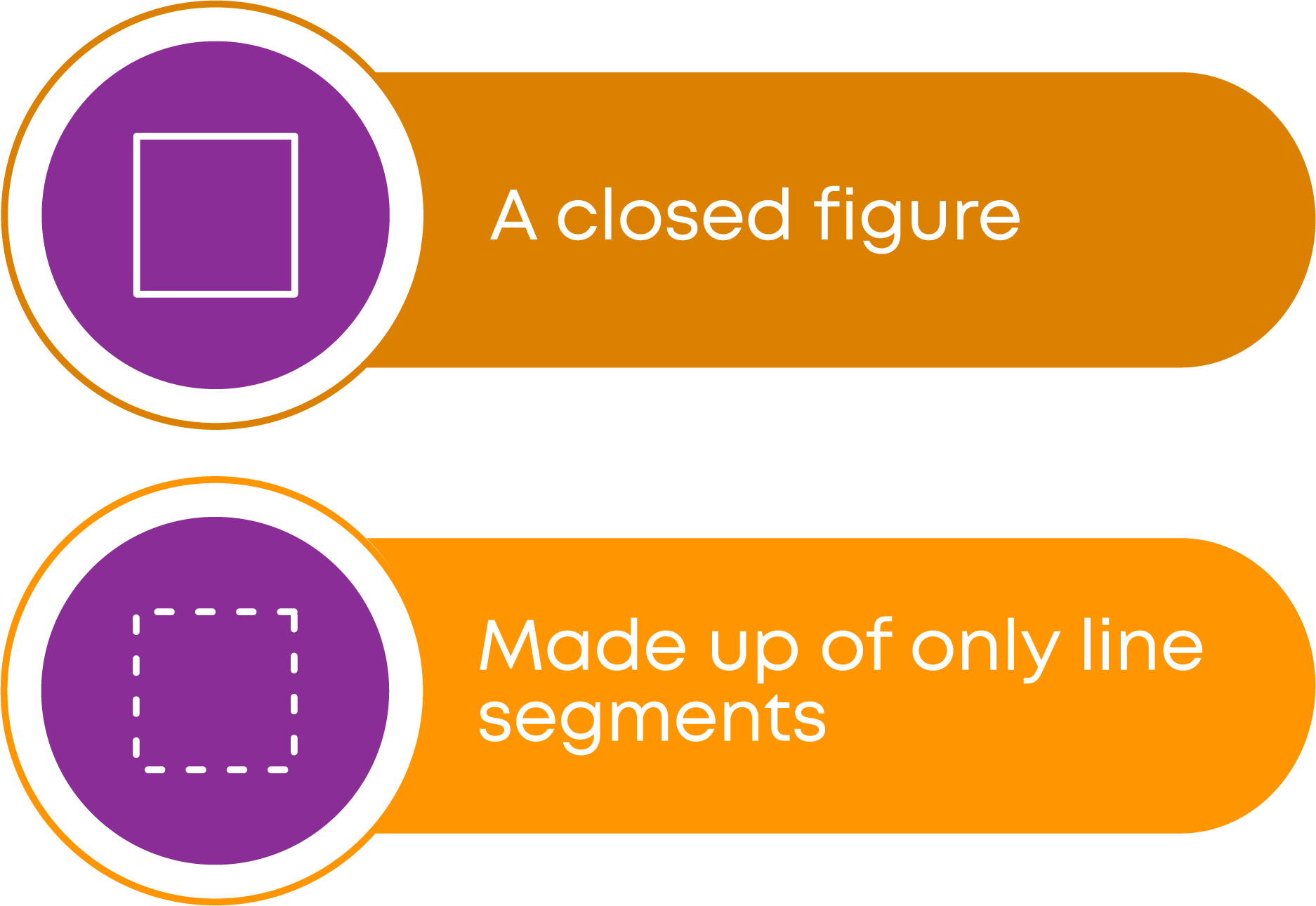
A polygon is a closed figure made up of only line segments. Examples:


For a figure to be called a polygon, it should be a closed figure.
We learnt about the properties of a polygon. So, to identify a polygon, we must check for those properties. If the given figure possesses all the properties, then the figure is a polygon. Properties to be checked in the given figure:
More About Polygons
The name given to a polygon with least number of sides (that is with three sides) is a triangle. Similarly, polygons with different number of sides have different names.
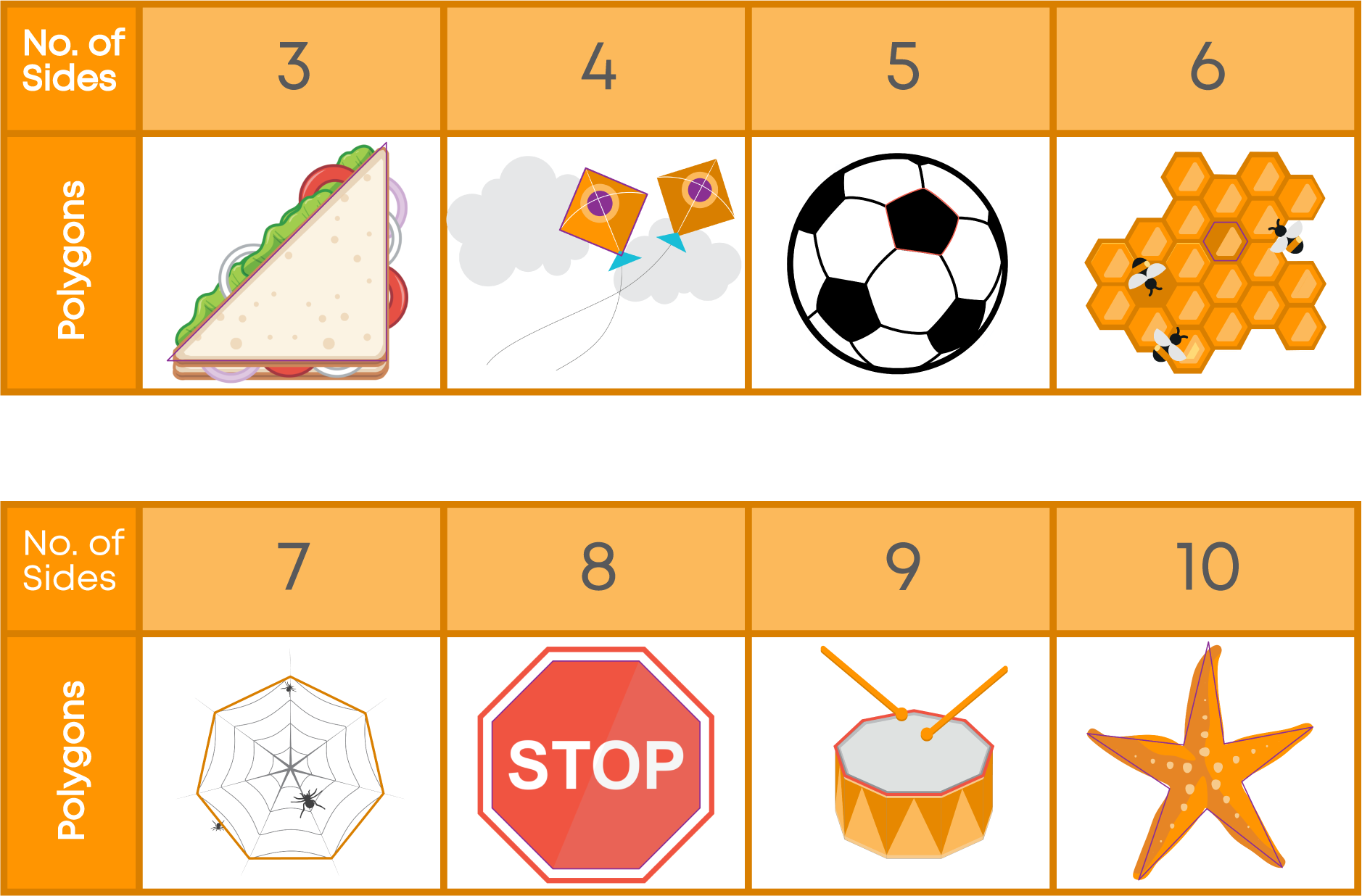
Now let us look at some polygonal shaped objects we see in our daily life.

Let us classify these figures according to the number of sides of the polygons.
Do you know why a polygon with three sides is called a triangle? The term ‘tri’ means three. So, triangle means three angles. A polygon with three sides has three angles, hence, it is called a triangle.
Similarly, other polygons are also named according to their number of sides.

In general, a polygon with ‘n’ number of sides is called an n-gon. Prefixes are Greek words for particular numbers. For example, ‘penta’ is a Greek word for ‘five’. So, a polygon with 5 sides/angles is called a pentagon.
Consider the pentagon below.
We see that every pair of sides of the polygon meet at a point. This point is called a vertex of the polygon. In any polygon, the number of vertices is equal to the number of sides of the polygon. Let us name the vertices of the polygon above.
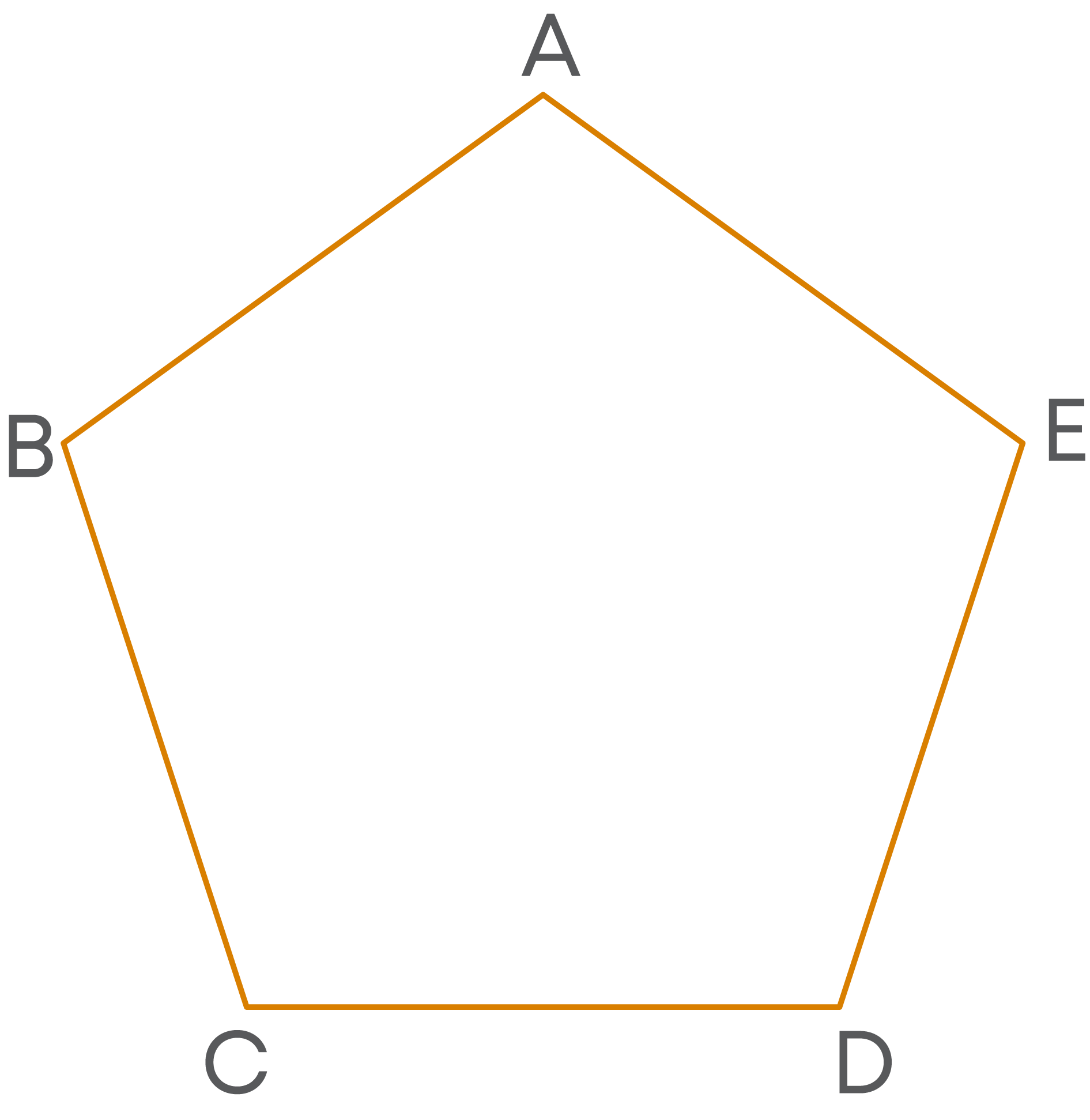
We can name this pentagon as pentagon ABCDE.
We observe that the line segments:
- AE and AB are sides of the polygon.
- AD and AC are not sides of the polygon.
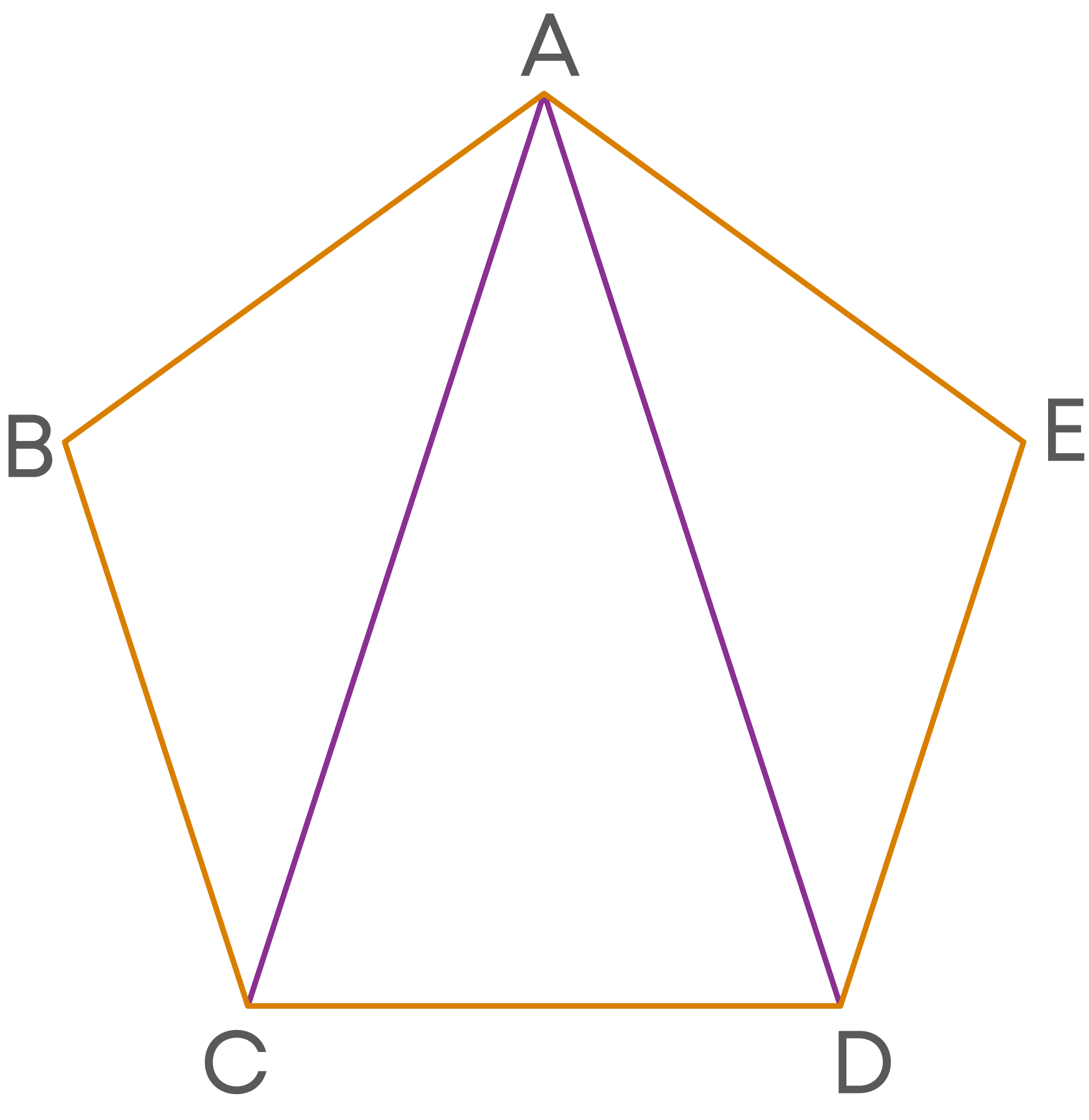
Here, all the four-line segments are drawn from the same vertex A to other vertices of the polygon. But two of them are sides of the polygon and the other two are not. How do we differentiate?
We can observe in the figure that, vertices B and E are adjacent (consecutive) to the vertex A. But the vertices C and D are not adjacent to the vertex A. Thus, each side of a polygon joins two consecutive vertices of the polygon. Then, what do we call those line segments which join two non-consecutive vertices?
They are called diagonals of the polygon.
A diagonal of a polygon connects only non-consecutive vertices of the polygon. Every line segment joining two non-consecutive vertices of a polygon is a diagonal of the polygon.
Example:
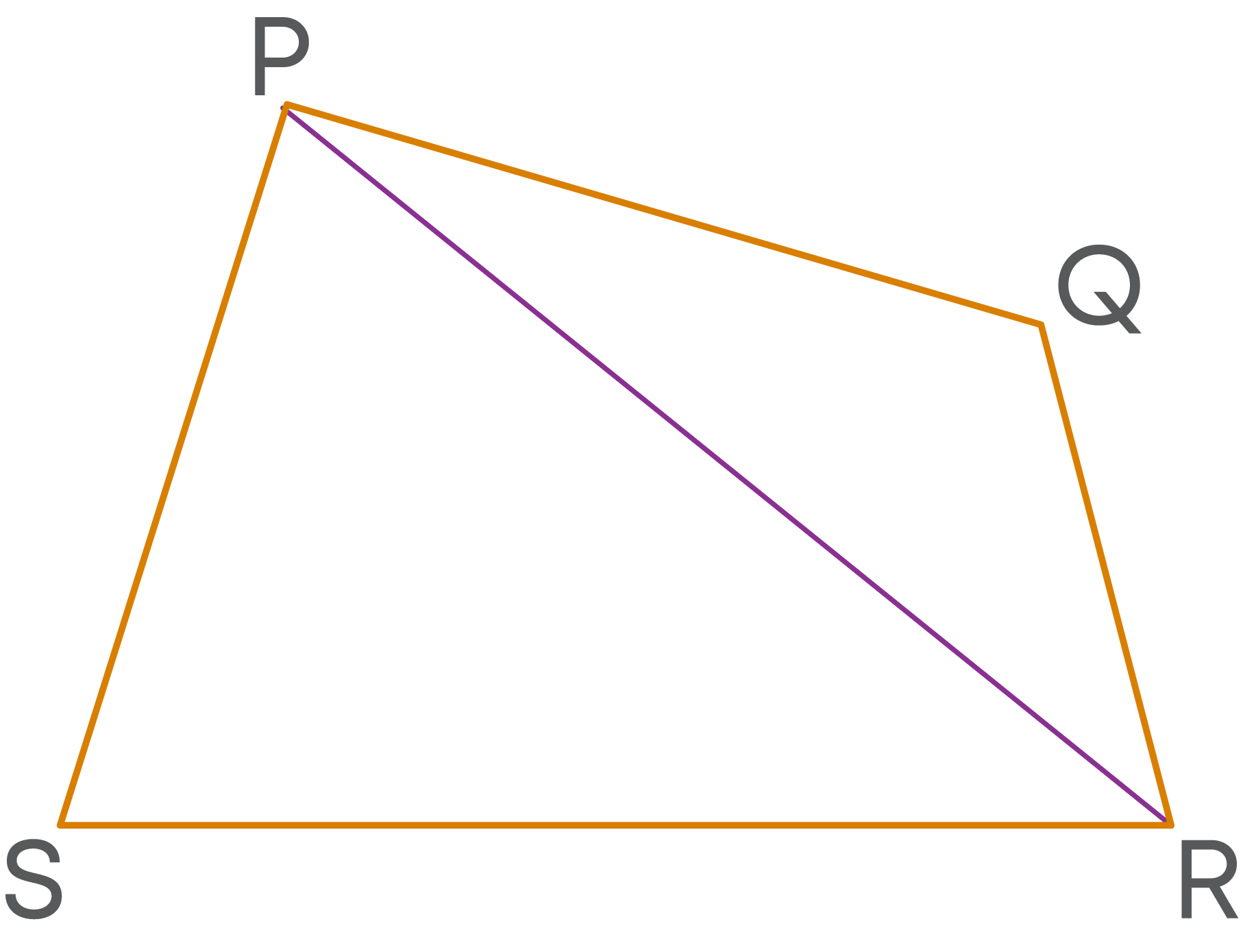
PR is a diagonal of the polygon PQRS.
Now consider a hexagon.
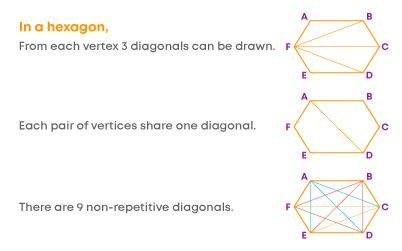
We can draw three diagonals from each of the 6 vertices of a hexagon. But we have a total of 9 non-repetitive diagonals.
The number of diagonals is different for different polygons. How does it vary?
Is there any relation between the number of sides of a polygon and the number of its diagonals? Let us start with a quadrilateral.
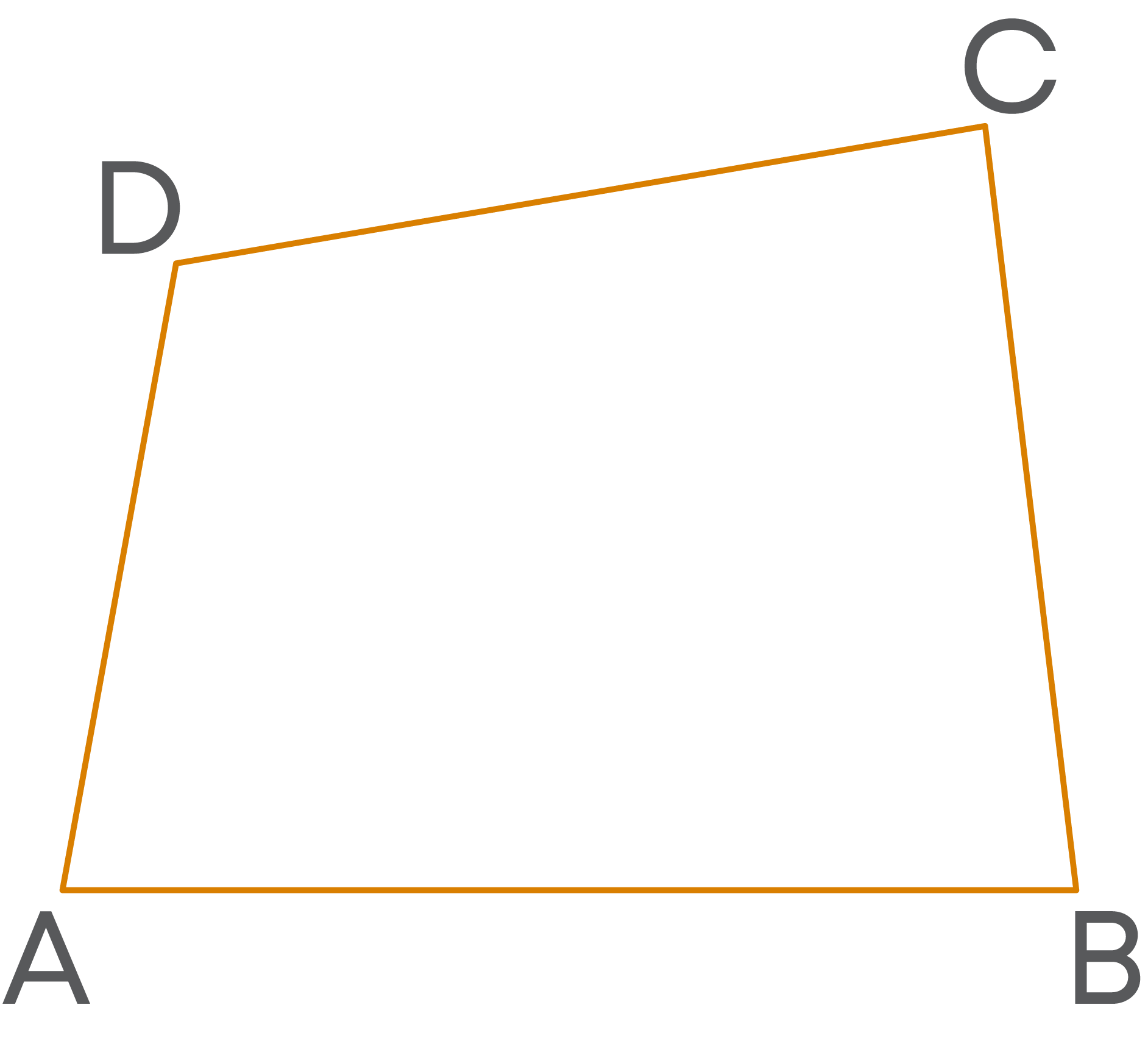
Consider a quadrilateral ABCD. How many vertices does it have? All quadrilaterals have 4 sides and 4 vertices. Now, consider the vertex A.
How many vertices of the quadrilateral ABCD are non-consecutive to the vertex A? Only one, that is the vertex C. So, from the vertex A, diagonals cannot be drawn to the vertices B and D. Also, diagonal cannot be drawn from any vertex to itself. Only to the vertex C, a diagonal can be drawn from the vertex A. This is similar for other vertices too. From any vertex of a quadrilateral, only one diagonal can be drawn.
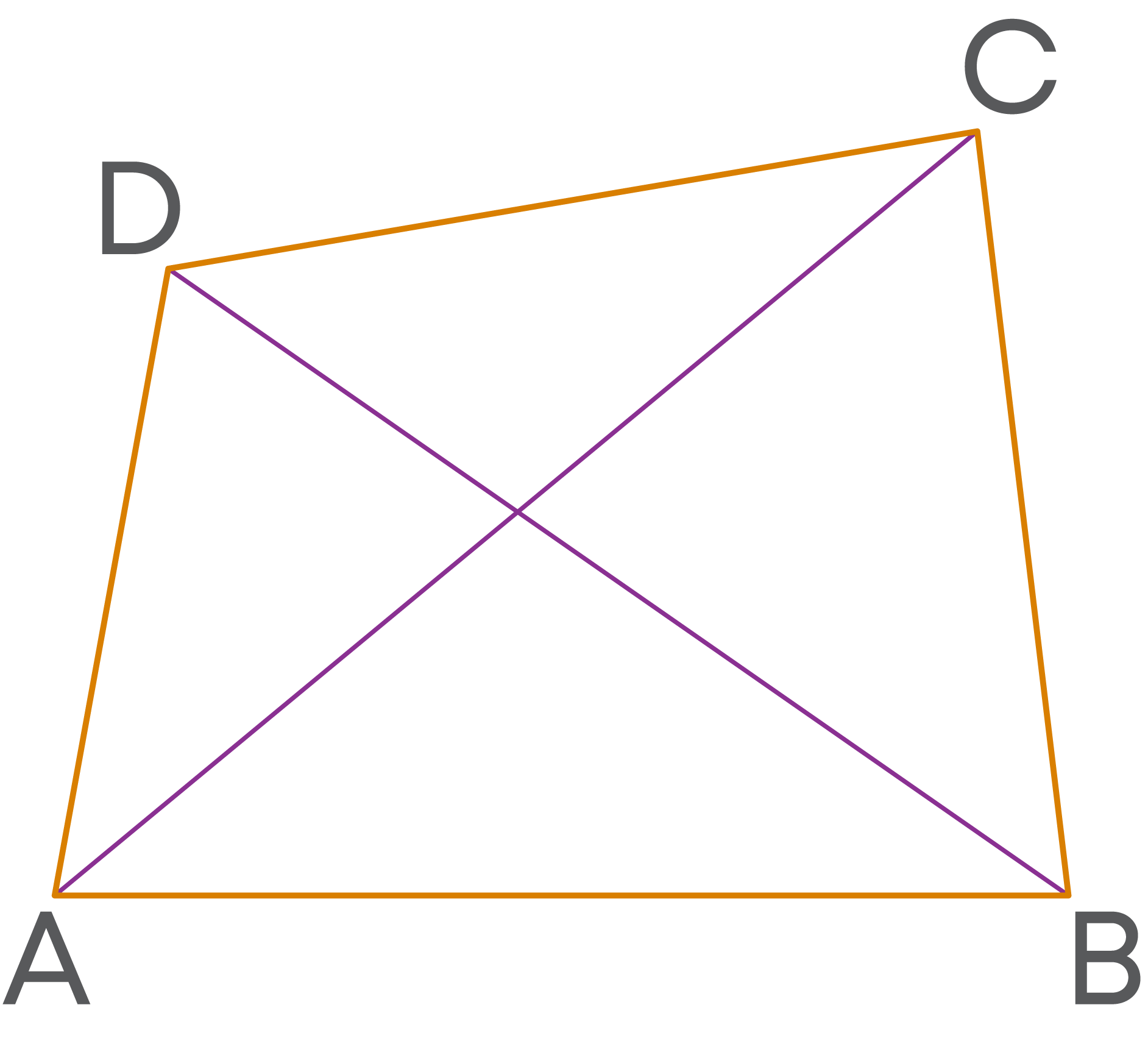
So, there should be a total of 4 diagonals in a quadrilateral. But we find only 2. Why is it so? Don’t forget that 2 vertices share each diagonal. If you count the same diagonal for both the vertices, then you will get the count of diagonals as double of what it actually is.
Hence, there are 2 diagonals for a quadrilateral.
Consider the pentagon PQRST.
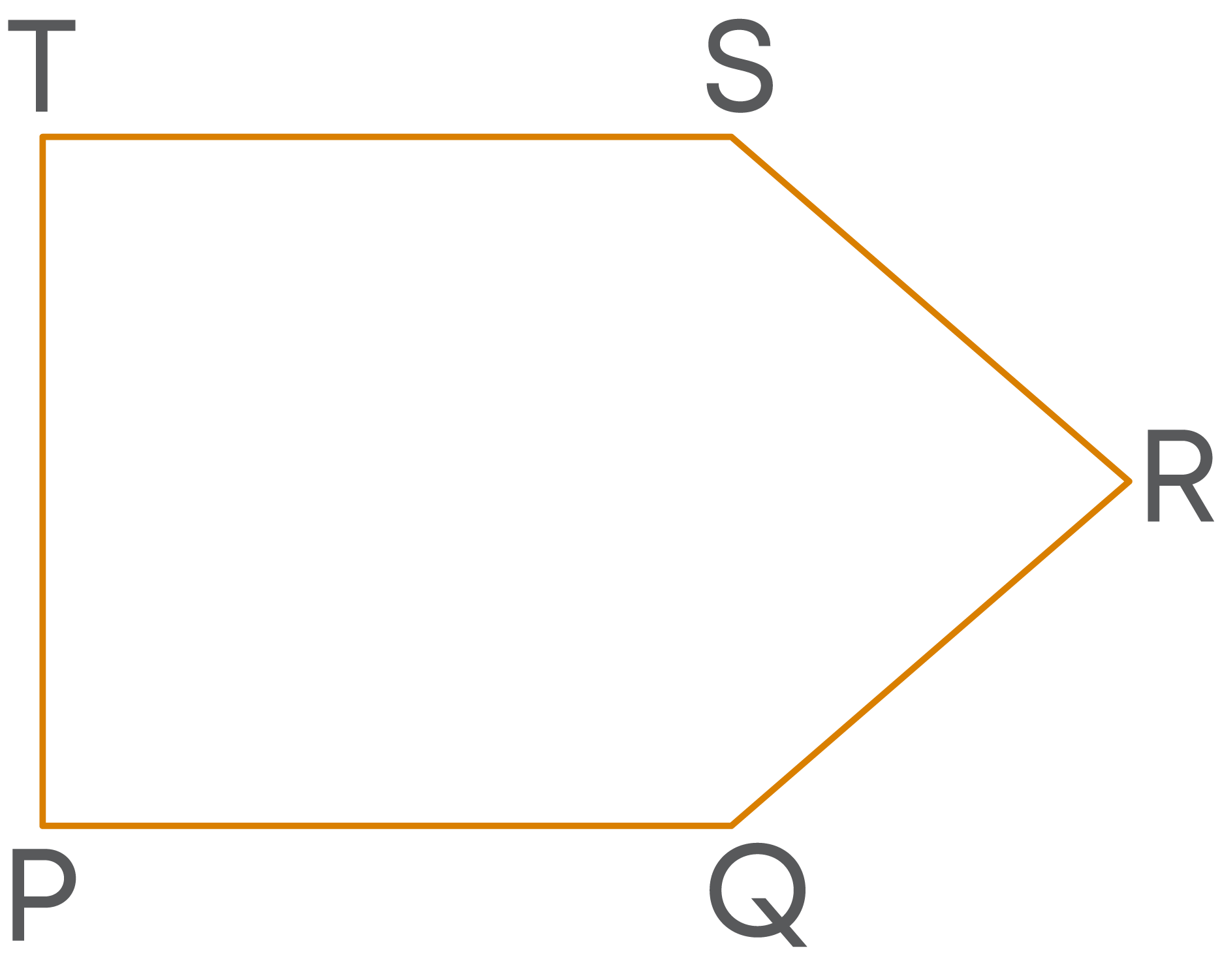
How many diagonals can be drawn from the vertex T?
Out of five vertices, P and S are consecutive to T. So, diagonals cannot be drawn to them from T. Also, diagonal cannot be drawn to itself. So, out of the 5 vertices, to three vertices diagonals cannot be drawn from T.
So, the number of diagonals possible from point T = 5 – 3 = 2
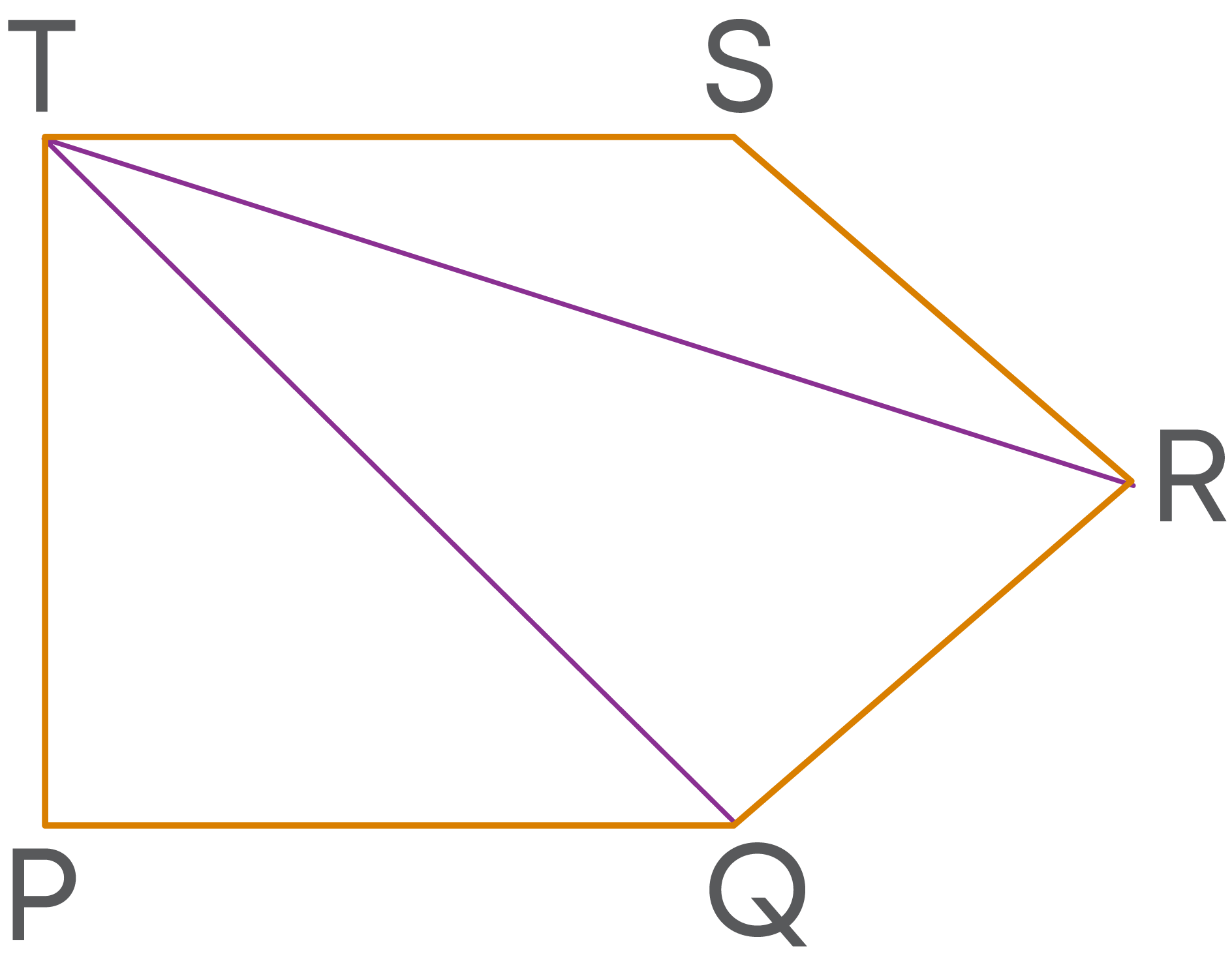
This is similar for other vertices too. So, from all the five vertices only two diagonals can be drawn.
There are 5 vertices in total.
So, the total will be 5 × 2 = 10.
i.e., 5 × (5 – 3)
But, in this way, while counting, we have considered each diagonal twice.
For example, diagonal TR is considered as the diagonal from T as well as from R. That means it is counted twice. This is the case for each diagonal. Hence, to get the actual count we must divide 5 × (5 – 3) by 2.
Thus, number of diagonals of a pentagon 5 × (5 – 3) 2 = 5
In general, for a polygon with ‘n’ sides,
- From each vertex (n – 3) diagonals are possible.
- There are ‘n’ vertices in total. So, the total count will be n(n – 3).
- Each diagonal is shared by two vertices. So, the total count gives the double of the actual number of diagonals of the polygon. That is why the total count must be divided by 2 to get the actual count of the diagonals in the polygon.
The number of diagonals of a polygon with ‘n’ sides = n × (n – 3) 2
Types of Polygons
Observe the figures below:

Do you find any difference between the two polygons given in the previous question?
Certainly, there is no difference in the number of sides of the polygons because both have 6 sides.
So, let us explore how these two polygons differ from one another.
To find the difference, you must observe the interior angles of the two polygons.
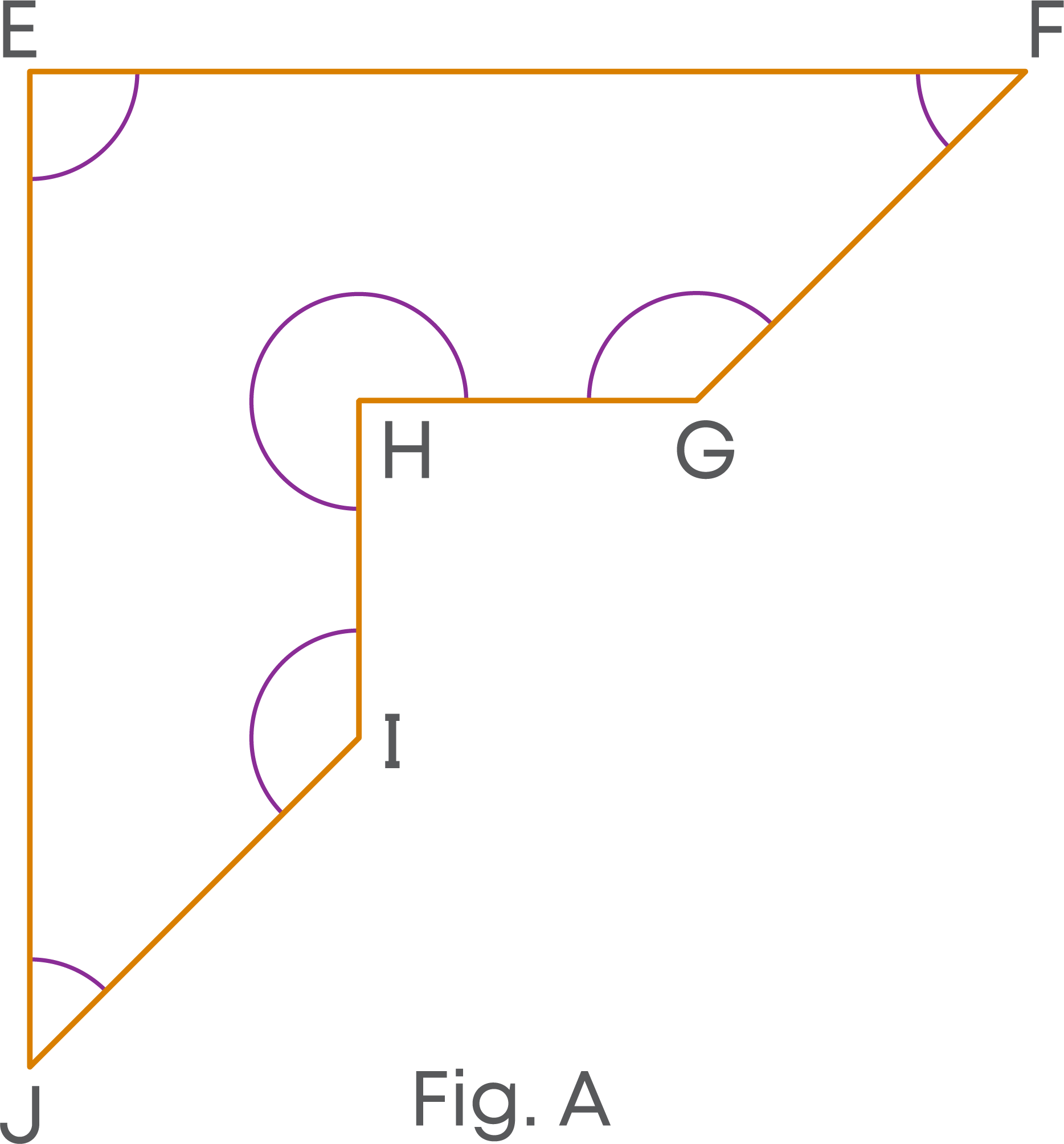
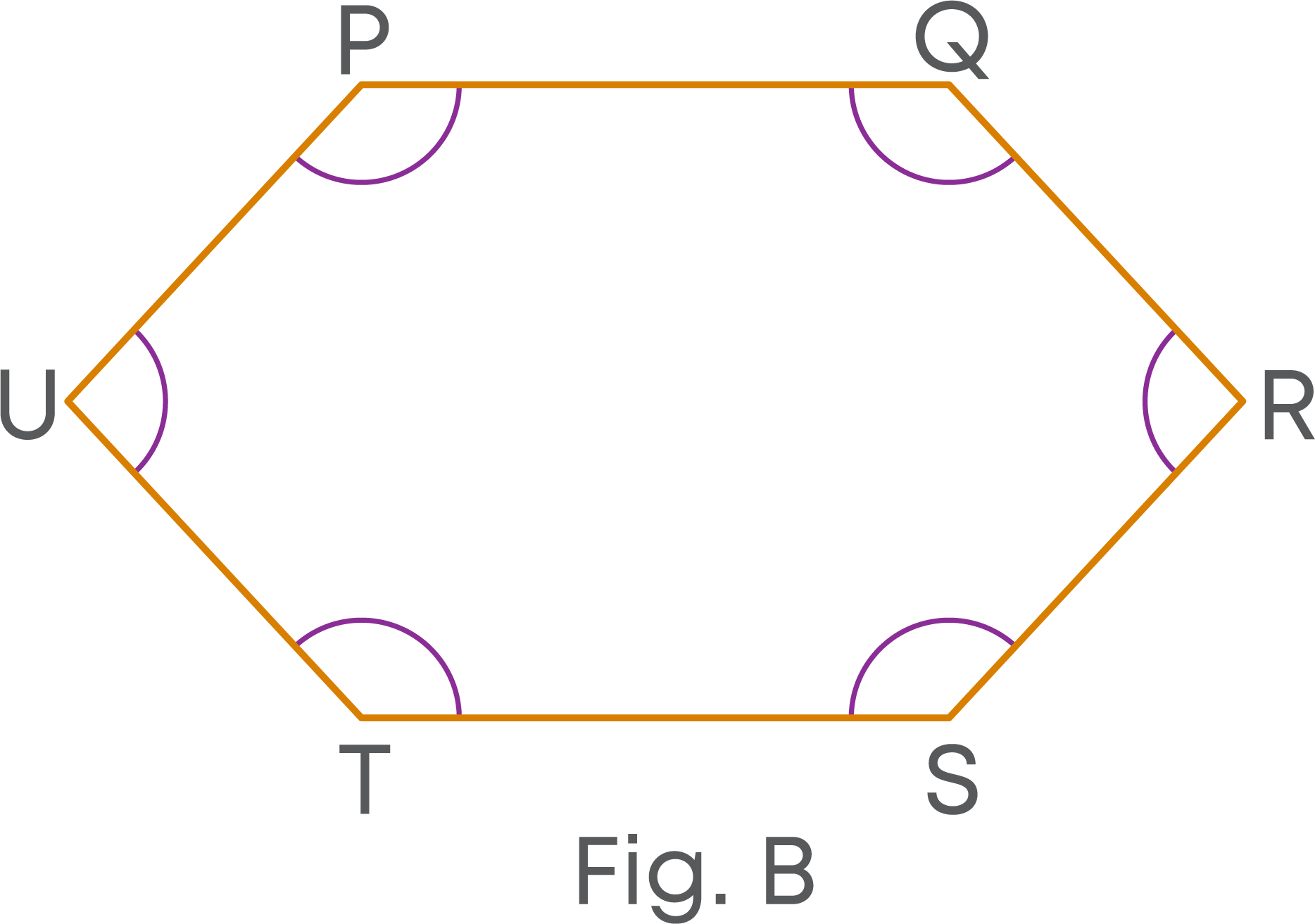
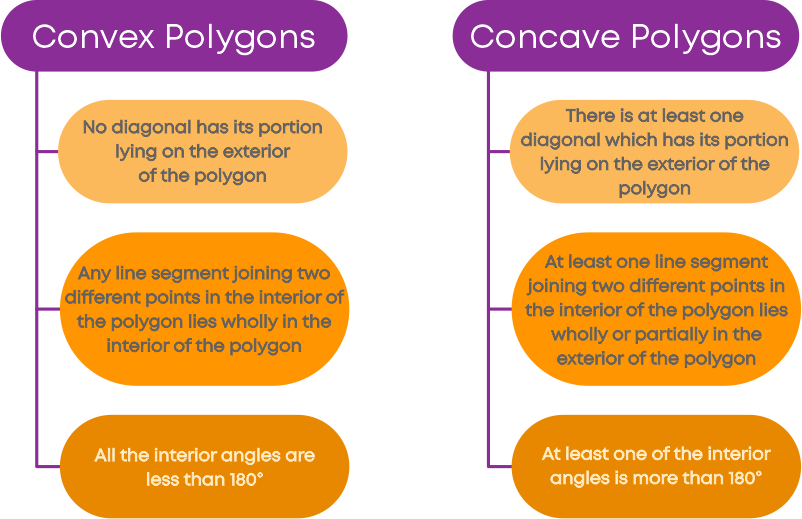
We find the difference between the two polygons is in their interior angles.
- In the polygon PQRSTU, none of the interior angles is a reflex angle.
- But, in the polygon EFGHIJ, one of the interior angles is a reflex angle.
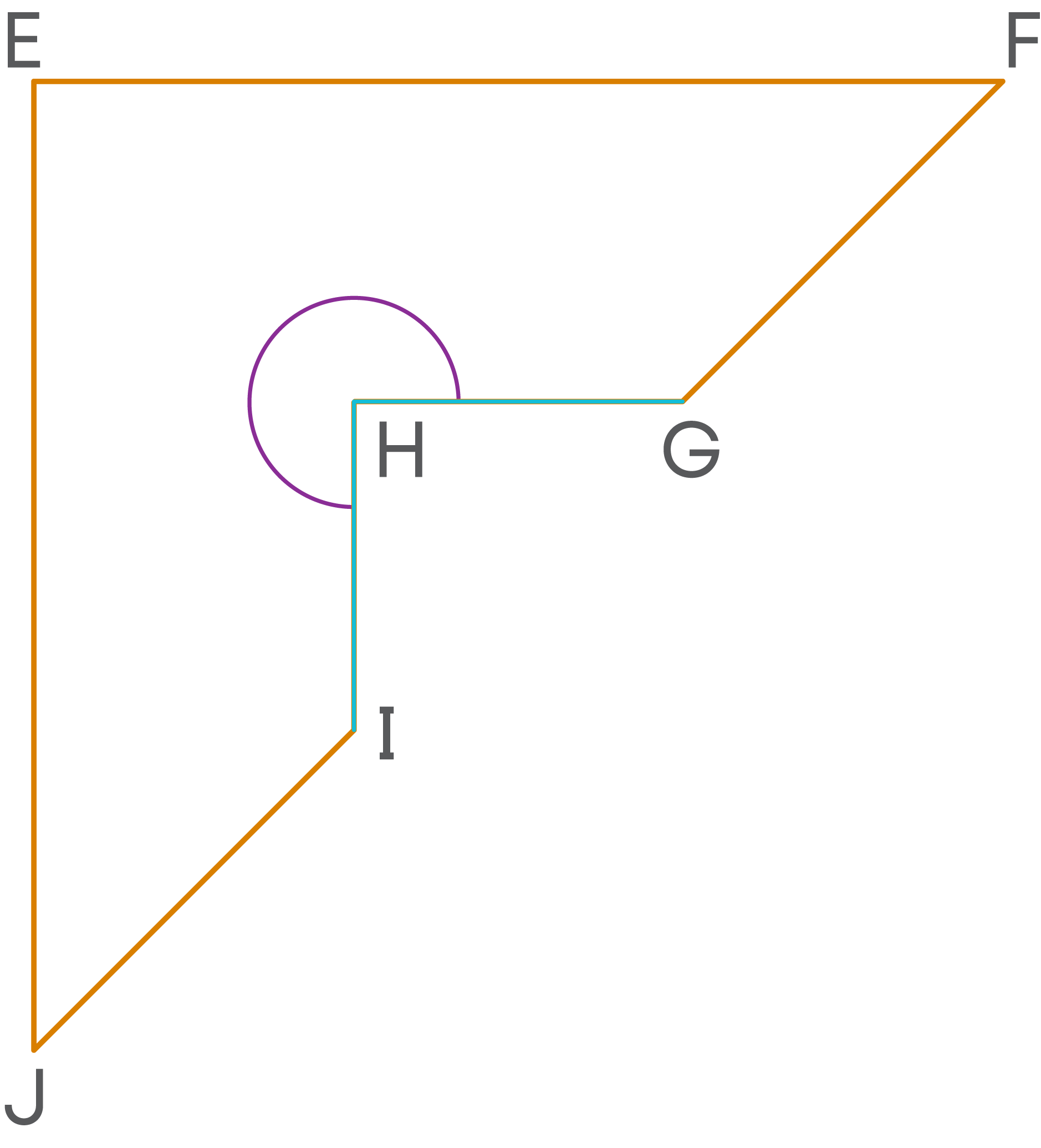
Such polygons are called concave polygons.
Diagonals of a concave polygon which we saw in the previous example are shown in the figure below.

Diagonals of few convex polygons are also drawn in the figures below.

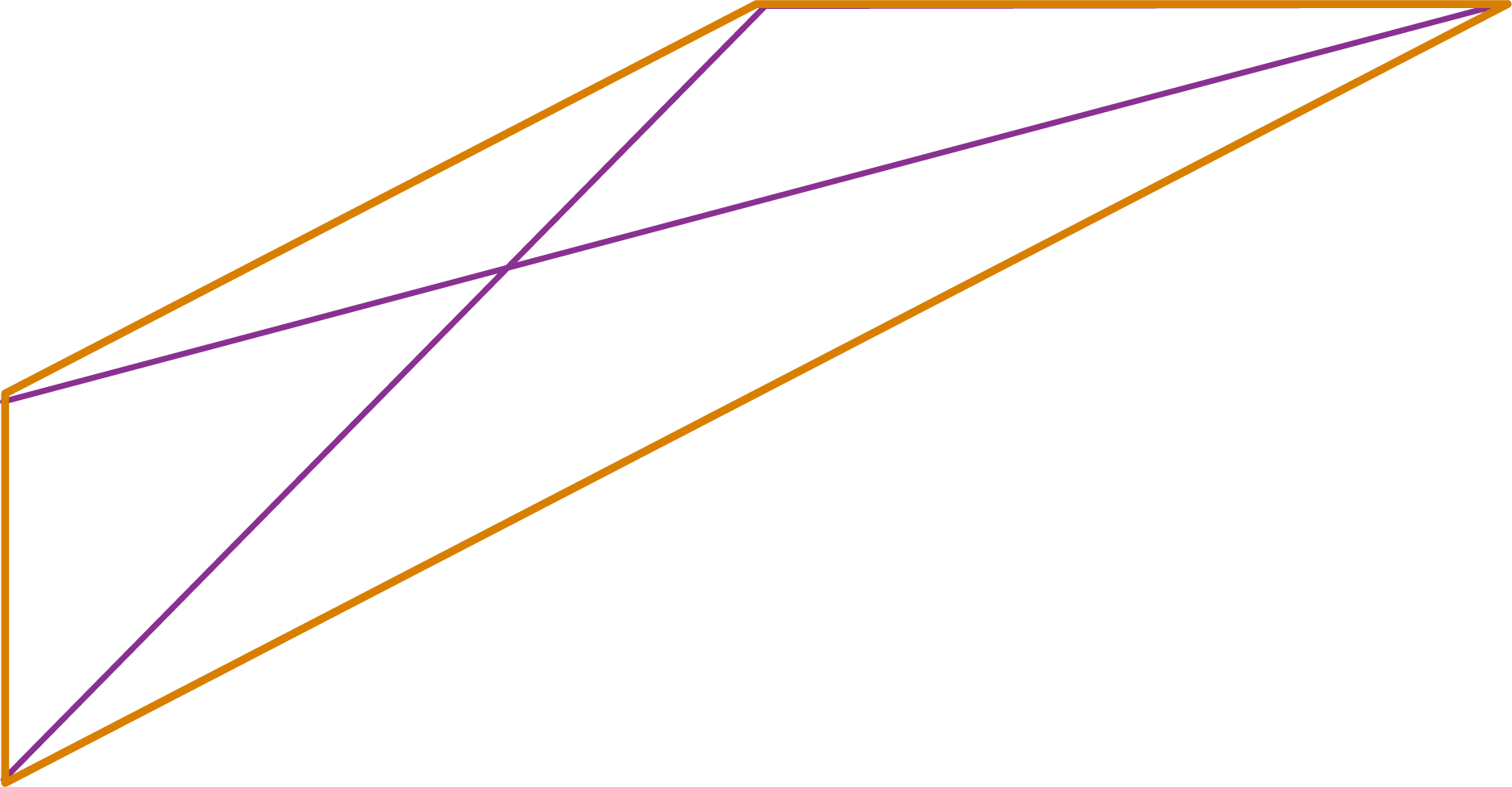
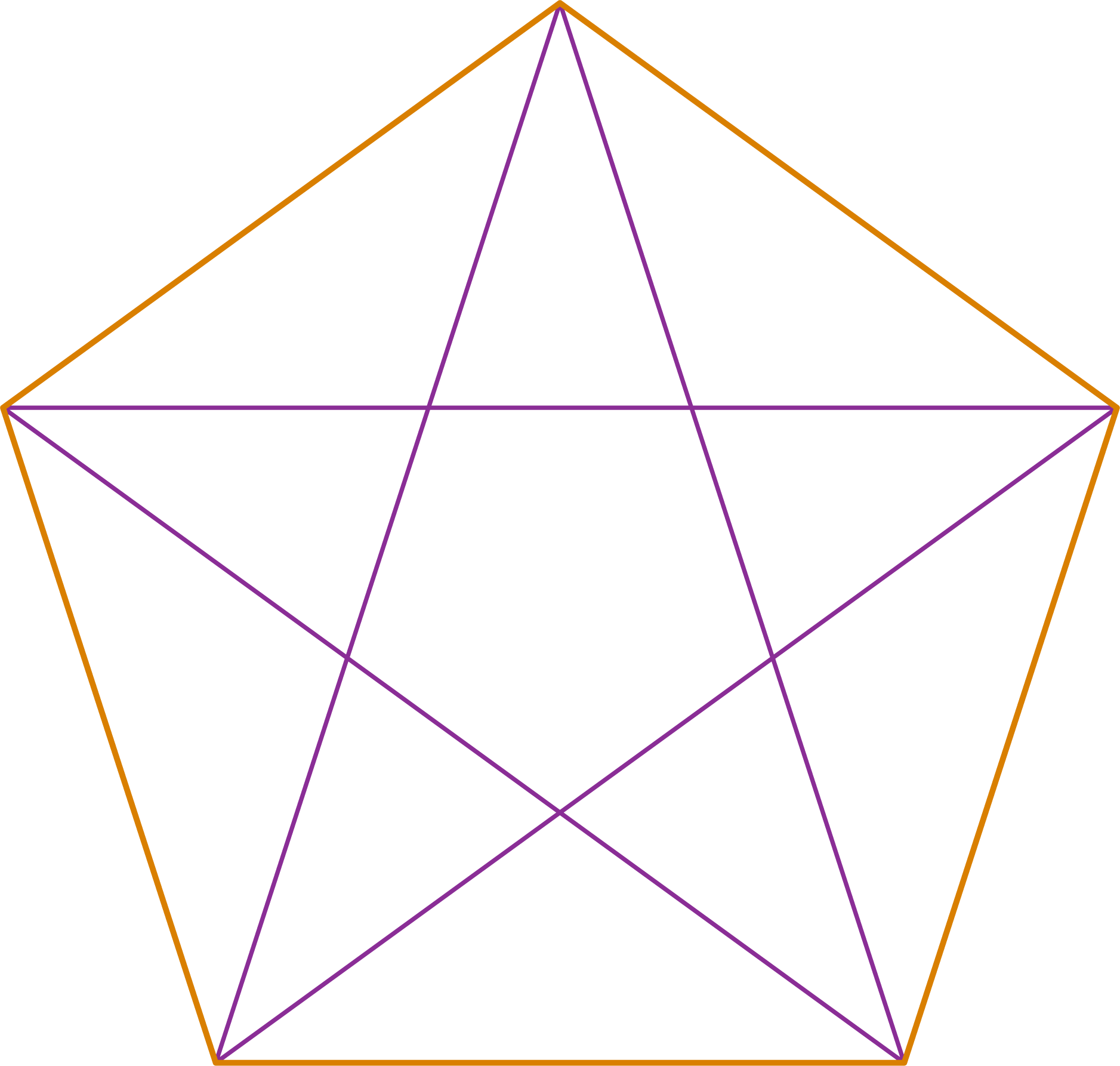
Do you find any difference between diagonals of the concave polygon and the diagonals of the convex polygons?
You can observe that no diagonal of the convex polygons has its portion lying in the exterior of the polygon.
What about the diagonals of the concave polygon?
You can observe in the concave polygon that few diagonals have their portion lying in the exterior of the polygon.

Now, consider two points A and B in the interior of the concave polygon as shown below.
Join the points with a line segment.
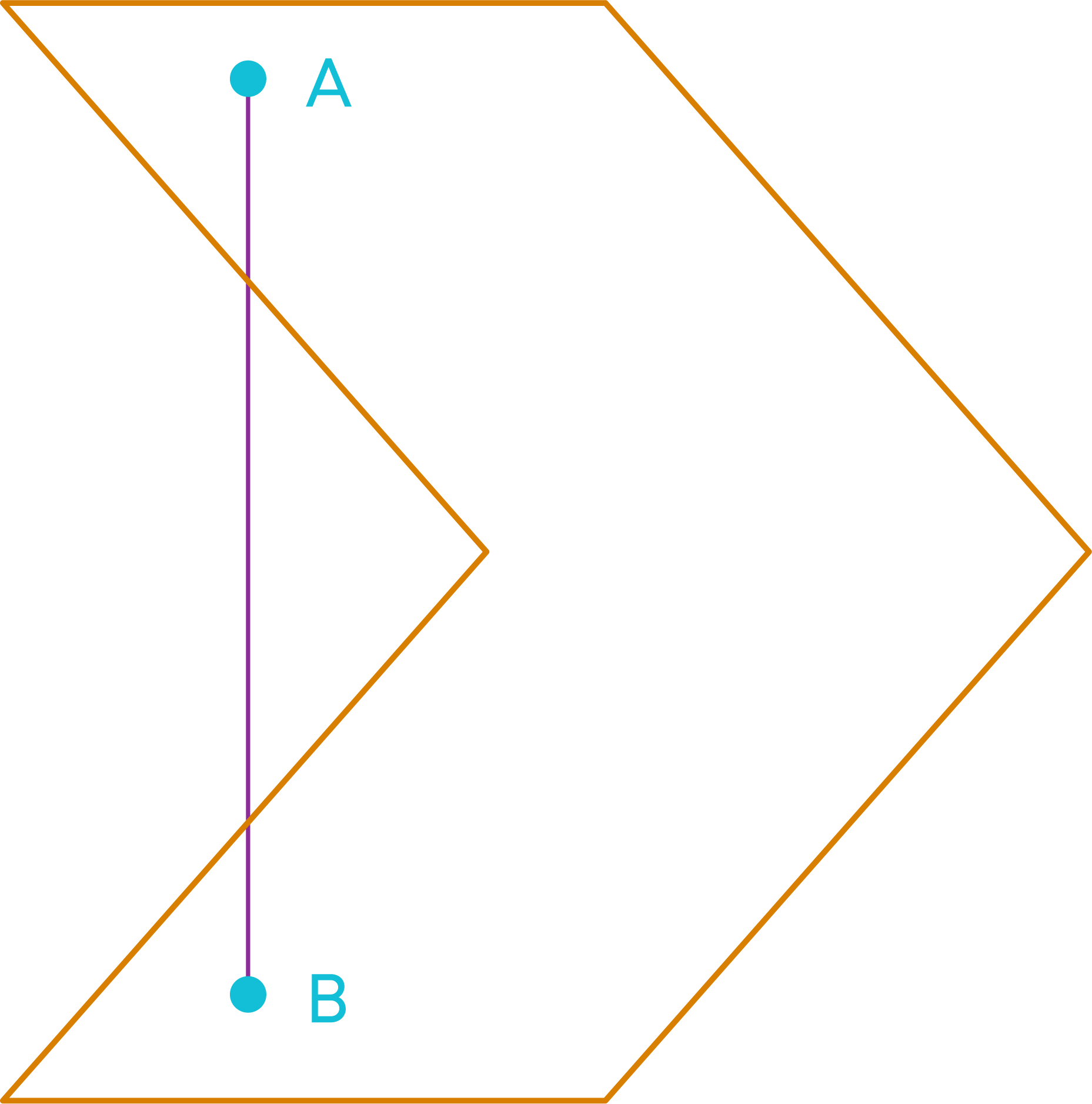
So:
- A polygon with at least one interior reflex angle is called a concave polygon.
- A polygon in which all the interior angles are non-reflex angles is called a convex polygon.
In other words, polygons with no reflex interior angle are convex polygons.
Let us list down the properties of convex and concave polygons.
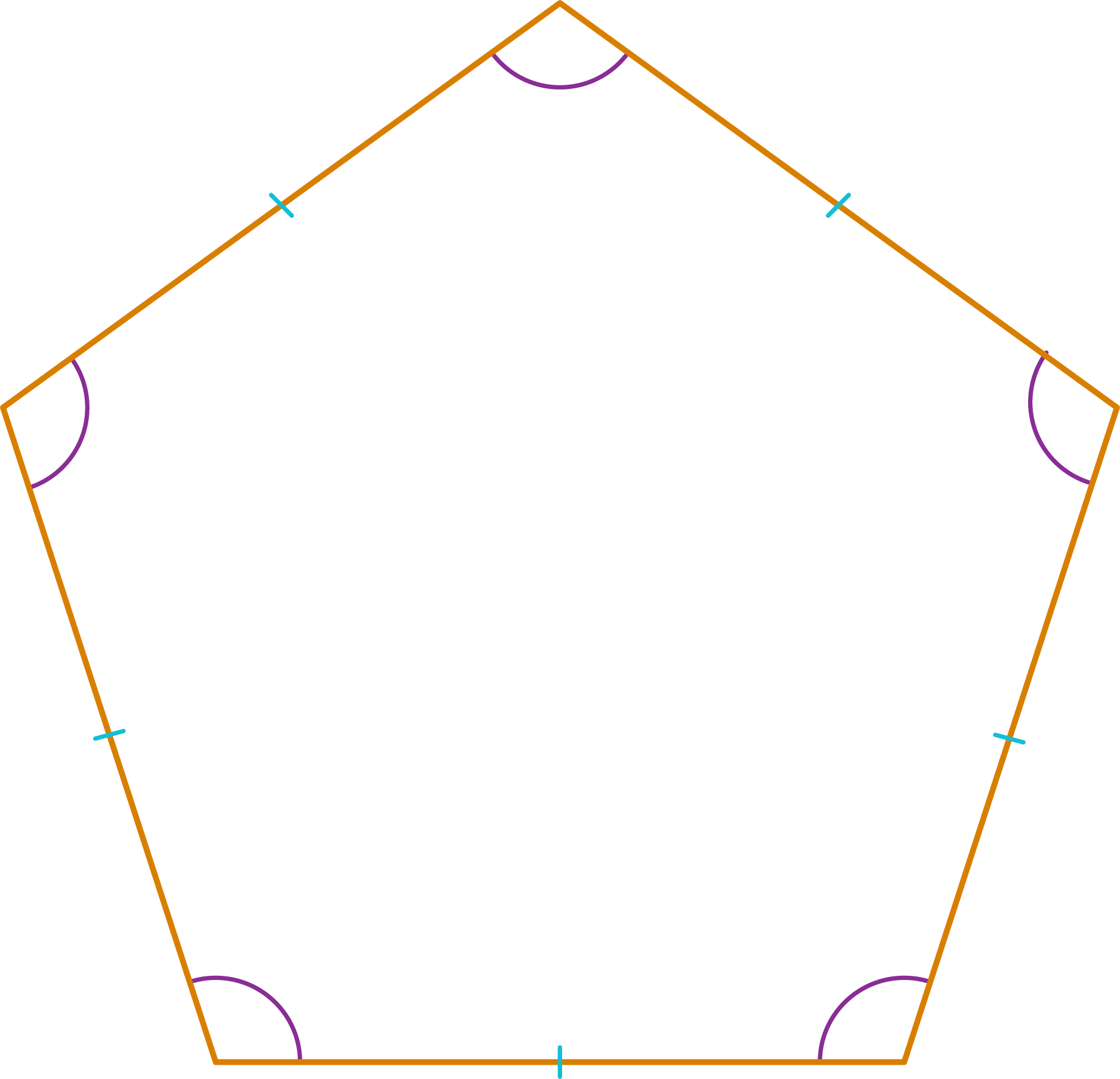
A polygon is said to be regular only if it is equilateral as well as equiangular. In other words, a regular polygon has equal sides as well as equal angles. Two very familiar examples for a regular polygon are an equilateral triangle and a square.
- An equilateral triangle, as its name itself says, it has equal sides.
- Equilateral triangles are also called equiangular triangles as they have equal angles.

- A square is a quadrilateral with equal sides and each interior angle measuring 90°.
- Thus, a square being equilateral and equiangular, is a regular polygon.

We will look at some more regular polygons.
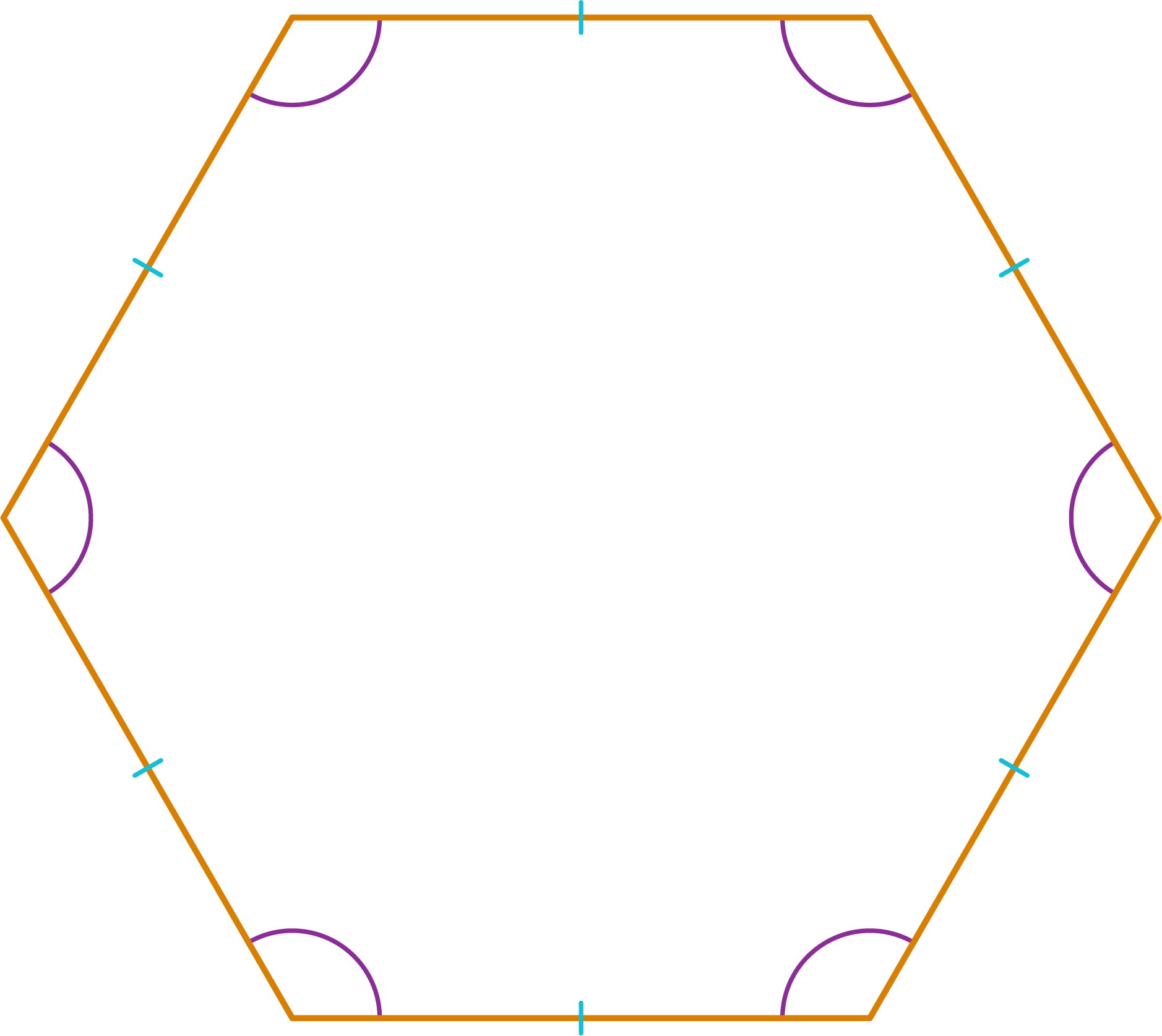
We know that polygons can be classified based on the number of sides as triangle, quadrilateral, pentagon, hexagon, and so on.
If these polygons are regular polygons, we add the prefix ‘regular’ to their respective names. For example, a pentagon with equal sides and equal angles is called a regular pentagon.
The following table gives you the names of regular polygons.

A rectangle has only its opposite sides equal and each interior angle measuring 90°. Thus, a rectangle is equiangular but not equilateral, hence, a rectangle is an irregular polygon.

Consider the following concave polygon with equal sides.

This polygon has equal sides but not equal angles. Thus, the concave polygon is equilateral but not equiangular. So, it is an irregular polygon.
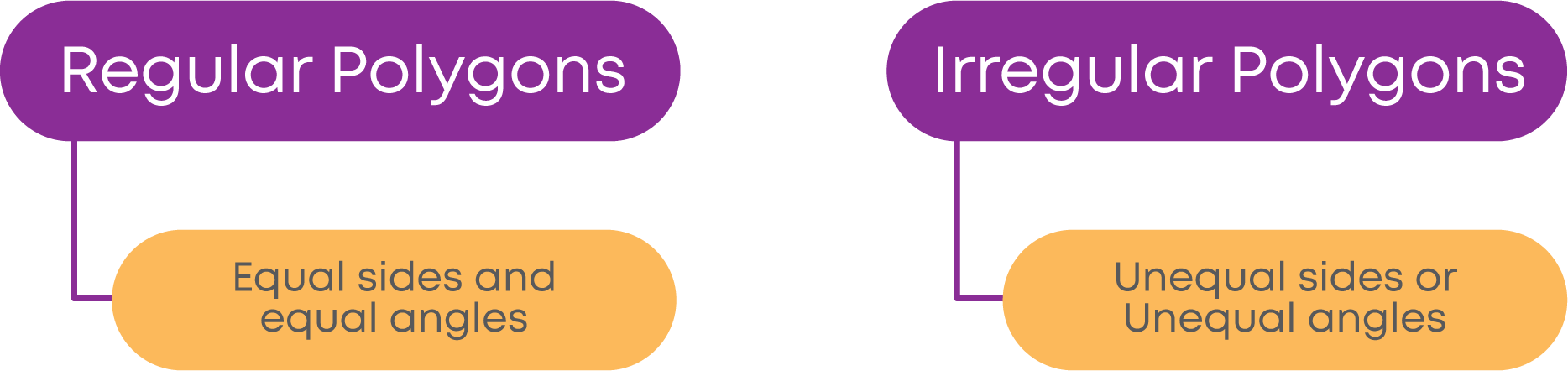
- A regular polygon will have all sides equal and all angles equal.
- An irregular polygon will have different lengths of sides or different measures of angles.
You know that the sum of all the interior angles of a quadrilateral is equal to 360°.
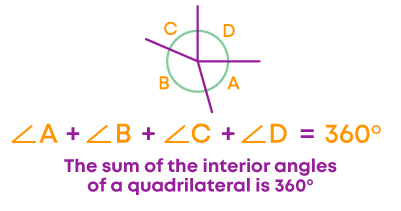
Now, let us consider a pentagon.
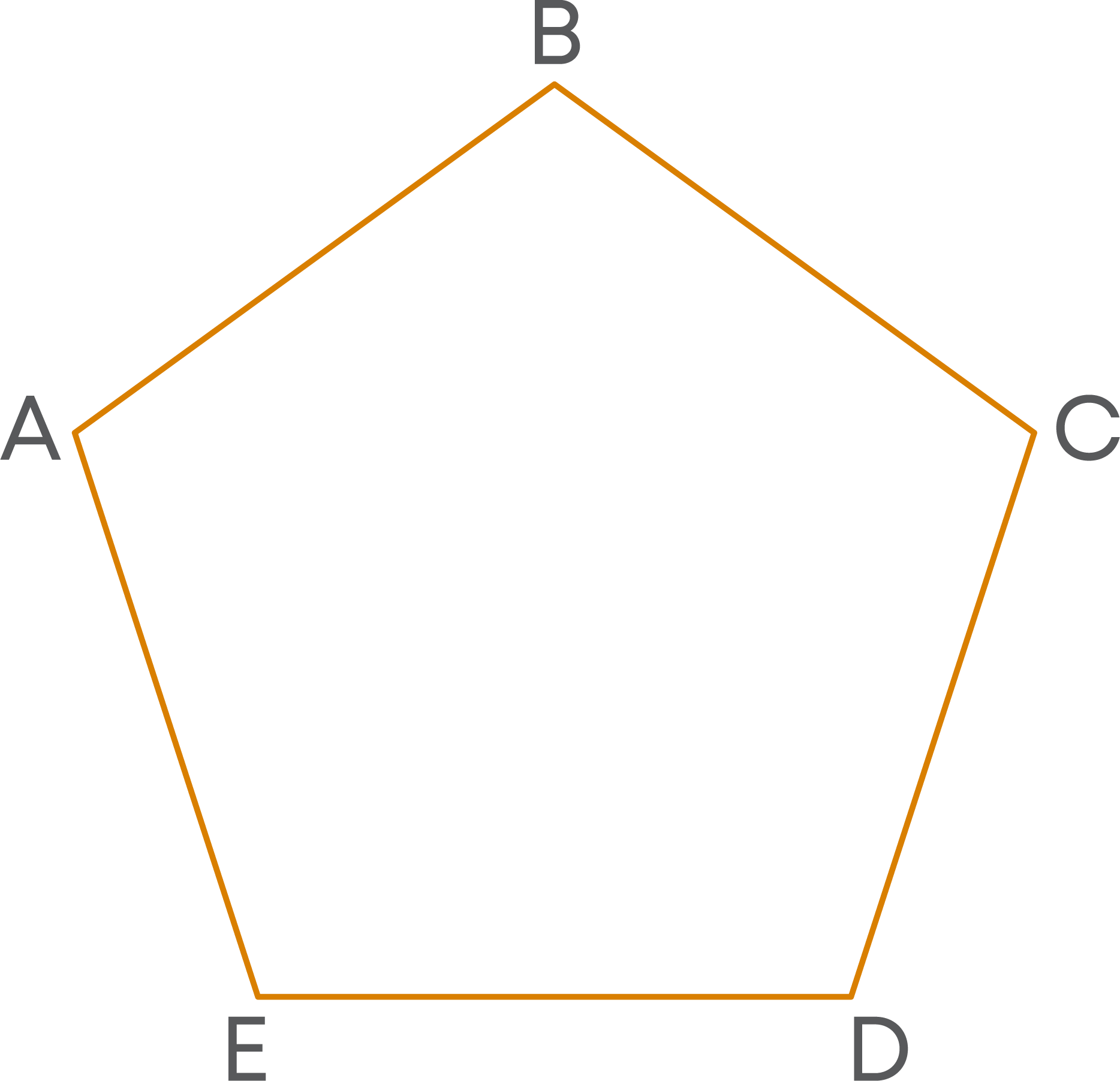
Now, from vertex A draw all the possible diagonals to divide the pentagon into triangles.
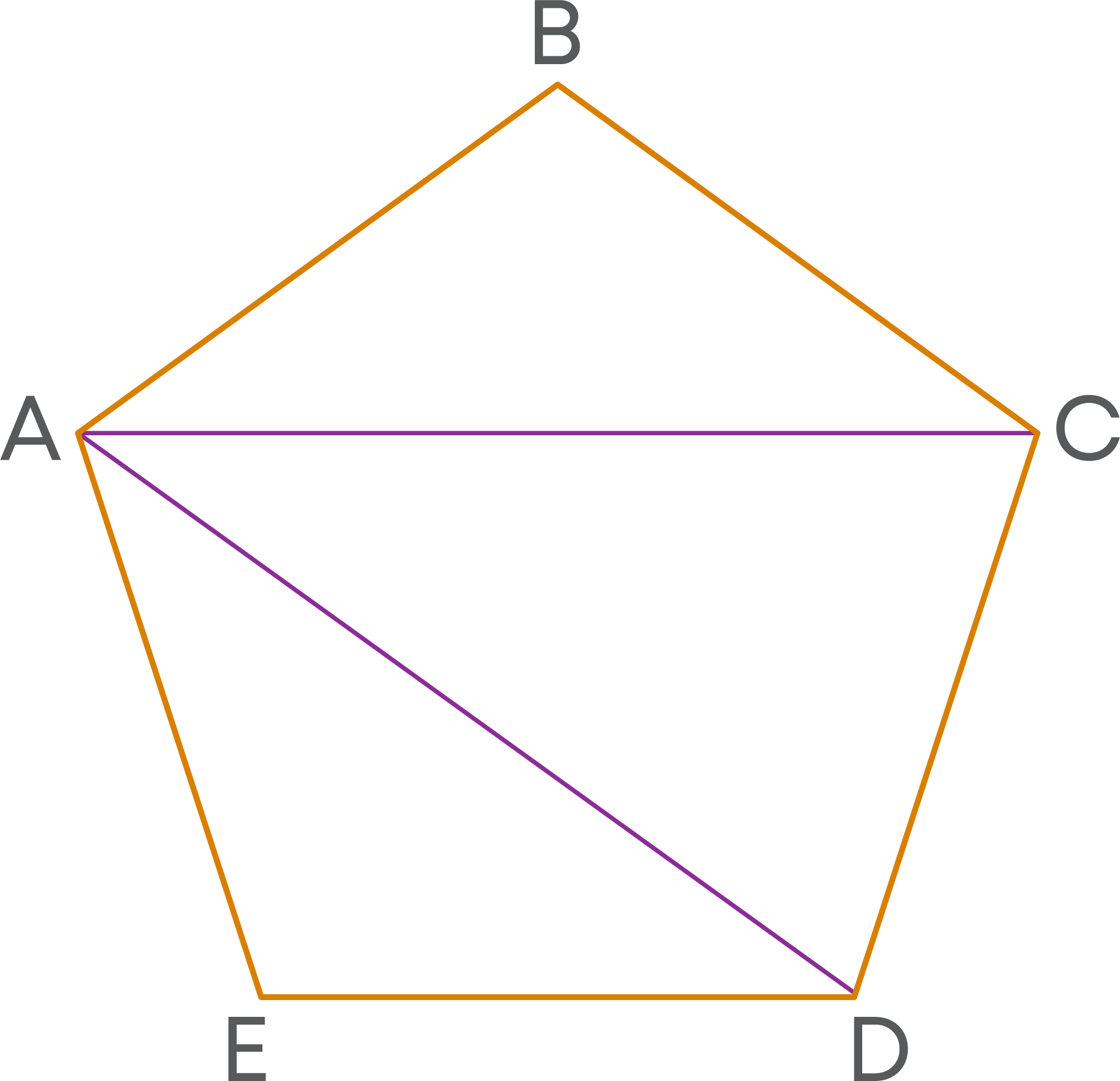
How many triangles did we get? Three.
Now, we can see that the interior angles of the polygon are divided as interior angles of all the triangles as shown in the figure below.

The sum of the interior angles of each triangle is 180°.
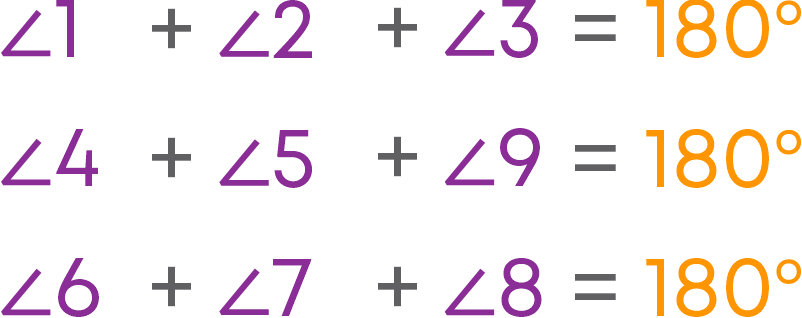
The interior angles of the three triangles sum up to give the sum of interior angles of the pentagon. There are 3 such triangles in the given pentagon.
So, the sum of interior angles of all the triangles = 3 × 180° = 540°
Thus, we get the sum of the interior angles of the pentagon as 540°.

For the two polygons we discussed, let us compare the number of sides/angles and the sum of the interior angles.
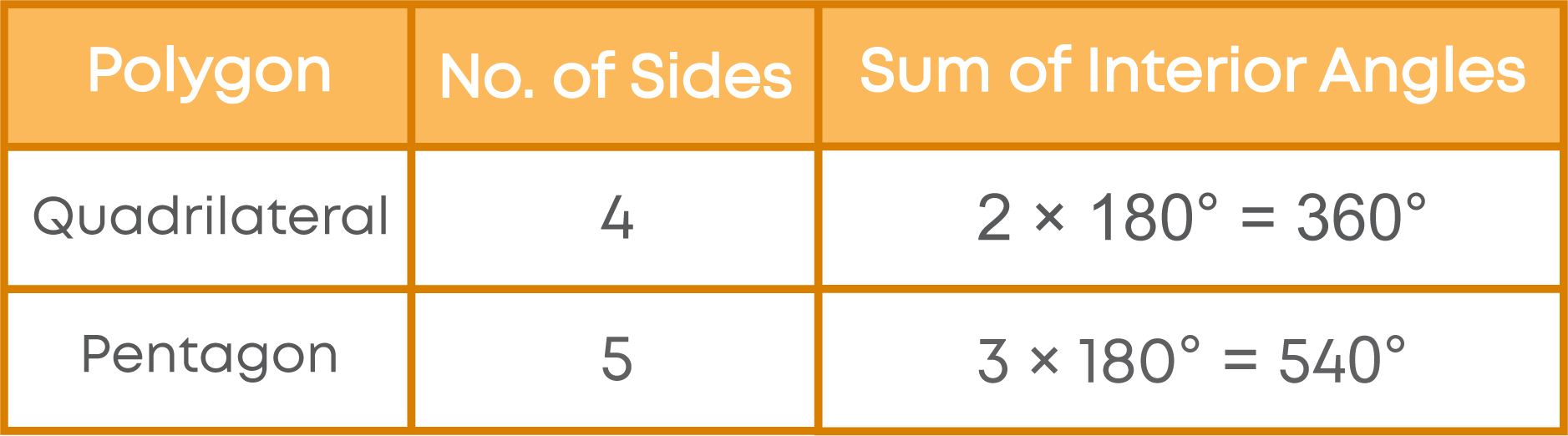
Now, let us have an example of a concave polygon. Consider:

Now, let us divide the polygon into triangles.
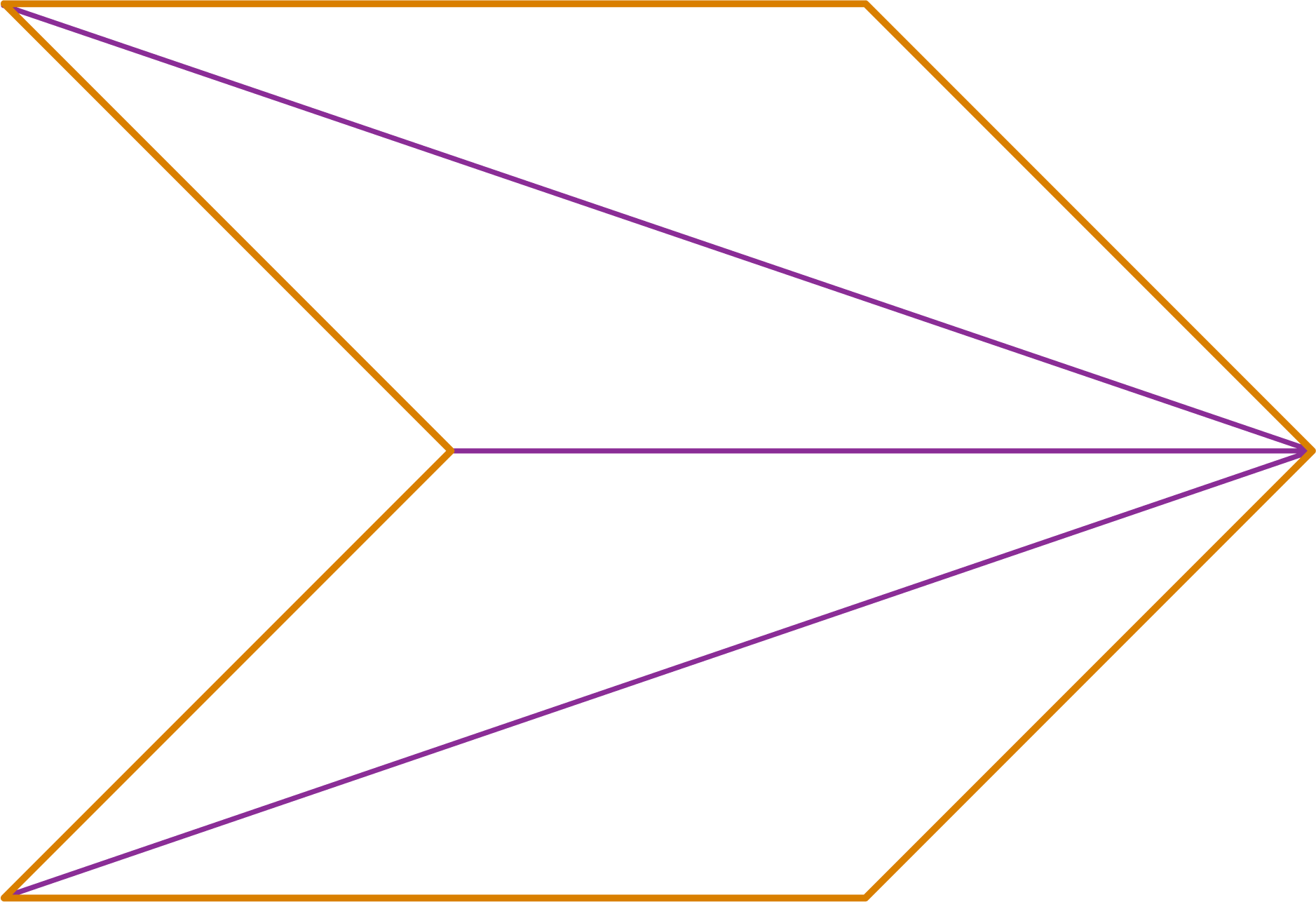
Here too, we observe that the interior angles of the polygon are divided as interior angles of triangles. The polygon has 6 sides, and it is divided into 4 triangles.
Hence, the sum of interior angles
= 4 × 180° = 720°
i.e., the sum of the interior angles
= (6 – 2) × 180°
The sum of the interior angles of a polygon with ‘n’ sides = (n – 2) × 180°
Also, (n – 2) = sum of the interior angles 180°
n = sum of the interior angles 180° + 2
So, we can rearrange the formula to find the number of sides of a polygon.
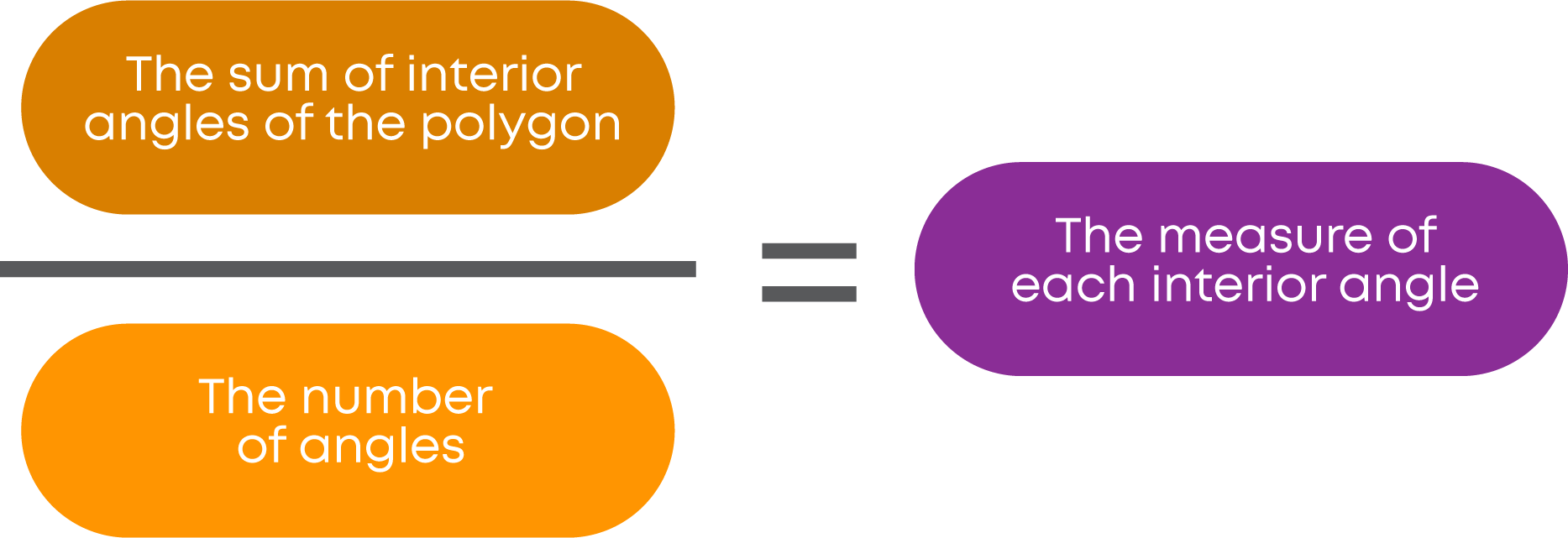
To find the measure of each interior angle of a polygon, divide the sum of the interior angles by the number of angles of the polygon:
Each interior angle = sum of the interior angles number of angles
To find the measure of the missing angle of a polygon with ‘n’ sides, when the sum of (n – 1) angles are given:
- Find the sum of the interior angles for a polygon with ‘n’ sides
- Missing angle = Sum of the interior angles – Sum of the remaining (n – 1) angles.
We know that when a side of a triangle is extended, an angle formed in the exterior of the triangle is called its exterior angle. Consider the polygon ABCD. Side BC of the polygon is extended to the point E.
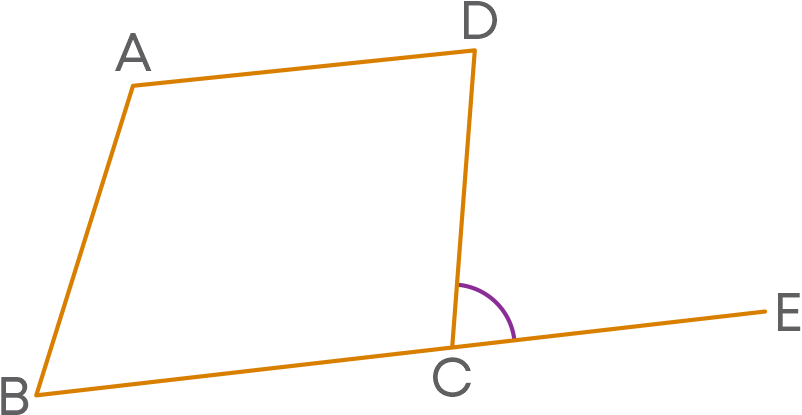
Now, ∠DCE is formed in the exterior of the polygon by extending a side of the polygon. So, it is an exterior angle of the polygon ABCD.
Now let us consider a pentagon.
Now, let us extend the sides of the pentagon as shown below to get exterior angles.
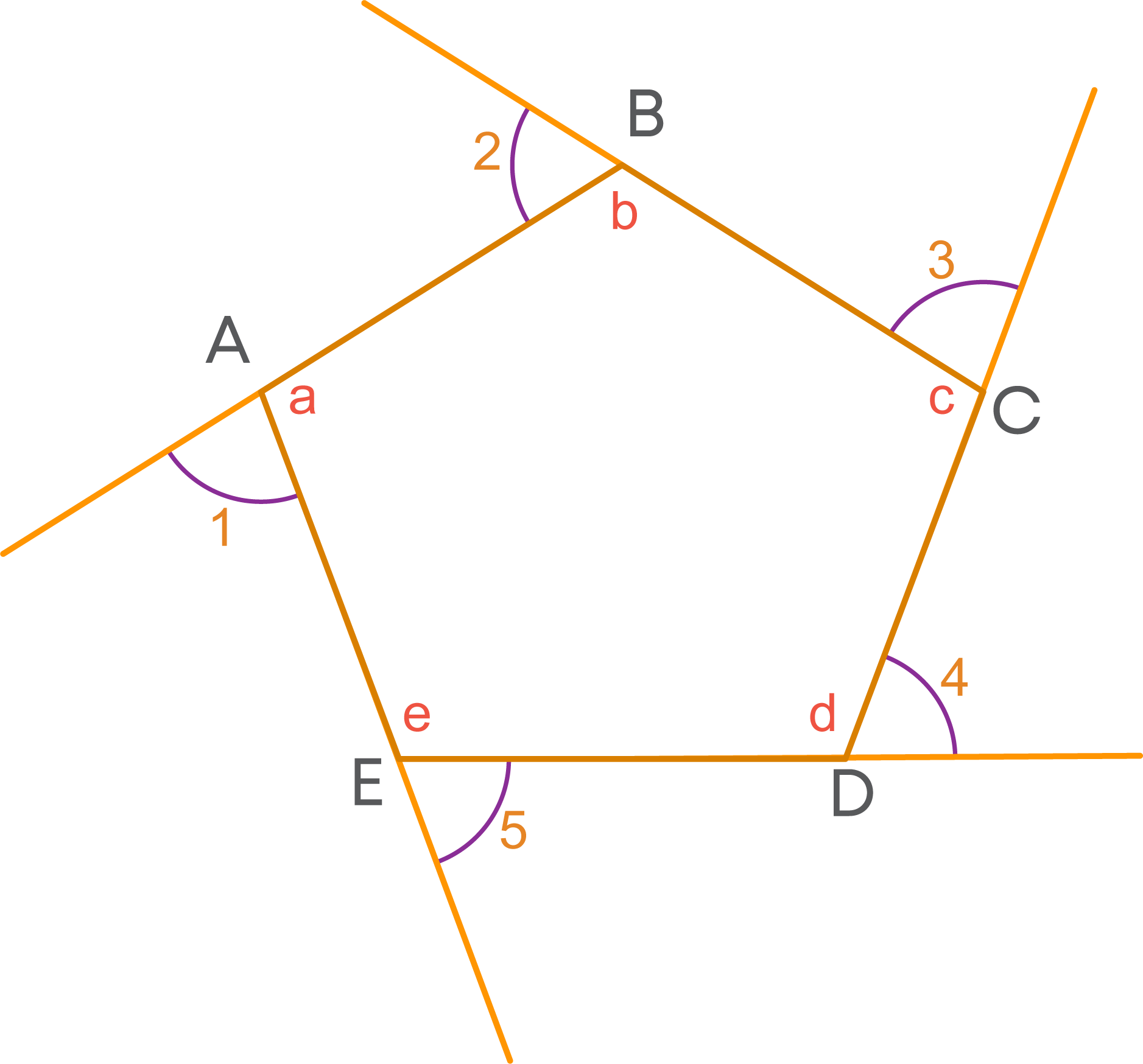
If we place all exterior angles adjacent to one another, we get a complete angle.
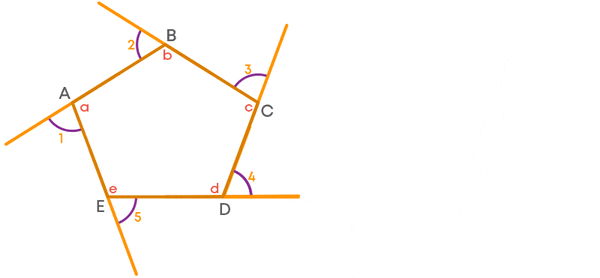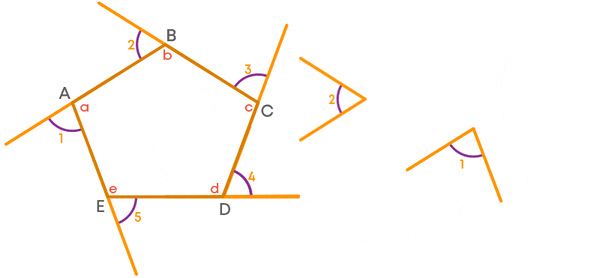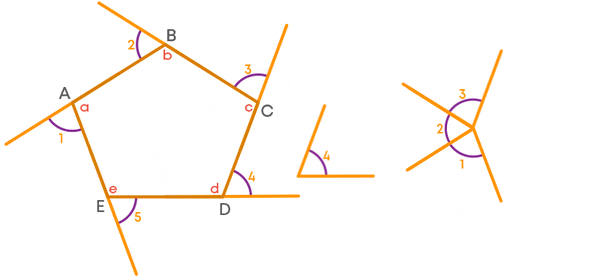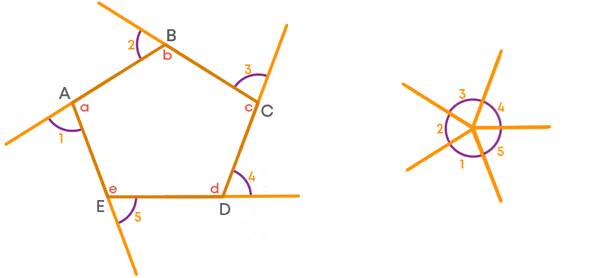
∠1, ∠2, ∠3, ∠4 and ∠5 sum up to give a complete angle.
i.e., the sum of ∠1, ∠2, ∠3, ∠4 and ∠5 is 360°.
(You can try to prove it logically, using the formula of the sum of the interior angles of a polygon.)
Similarly, for any other polygon, the sum of the exterior angles is 360°.
To find the measure of one exterior angle of a polygon, when the measures of the other angles are given, follow these steps:
First, find the sum of the exterior angles whose measures are given.
Then, subtract the sum from 360⁰ to get the measure of the missing angle.
In a polygon, the number of sides, the number of interior angles and the number of exterior angles are equal. Thus, for a regular polygon having ‘n’ number of sides, the number of exterior angles is also ‘n’.
The sum of measures of external angles of any polygon is 360°.
Hence, we get,
n × measure of each exterior angle
= the sum of all exterior angles

Hence, we get
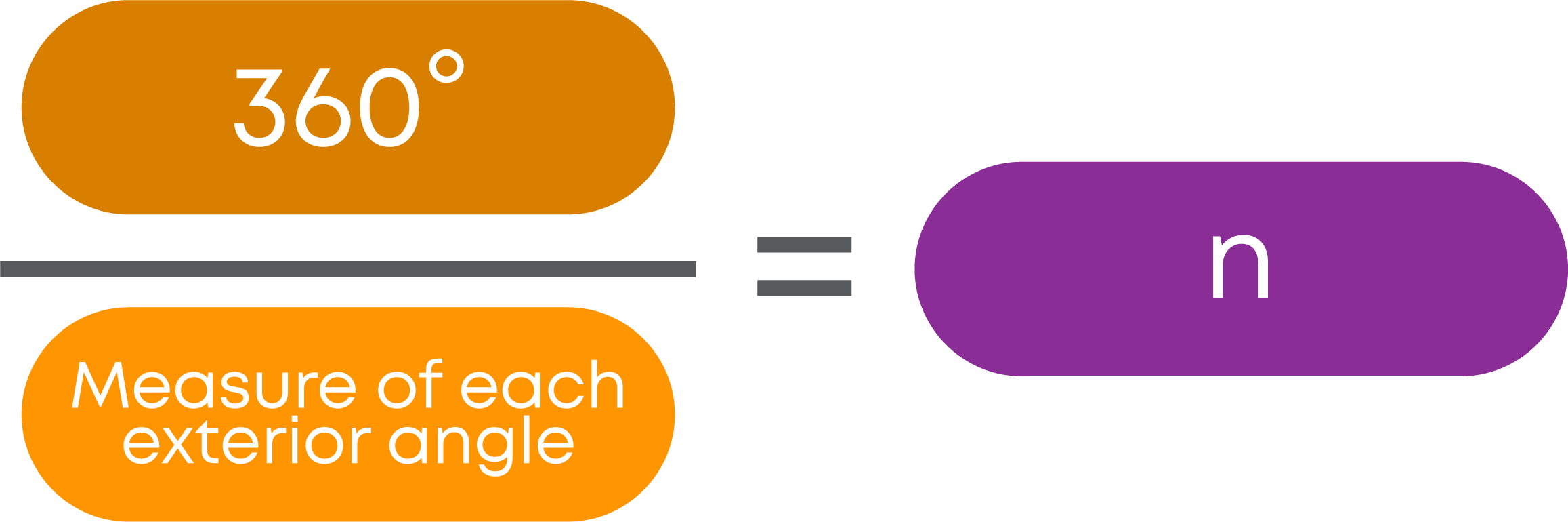
The number of sides of a regular polygon is obtained by dividing 360° by the measure of each exterior angle.
Now,

Hence, we have,

Now, you know how to find the number of sides of a regular polygon when an exterior angle is given.
We know that an interior angle and corresponding exterior angle of a polygon form a linear pair.
Thus, we have the following relation between them.
Interior angle + Exterior angle = 180°
Using this relation between an interior angle and corresponding exterior angle, we can find the number of sides of a regular polygon when the measure of an interior angle of the polygon is given by following these steps:
Calculate the measure of the corresponding exterior angle.

Use the result “The sum of exterior angles of a polygon = 360°”.

Calculate the value of 'n'
- Exterior angles of a regular polygon are equal.
- The number of interior angles is the same as the number of sides.
Use the relation

Kinds of Quadrilaterals
Trapezium
- A trapezium is a quadrilateral with one pair of opposite sides parallel.
- The other pair of sides will be non-parallel.
- The sum of the angles on the same side joining the parallel sides will be 180°.
- Since it is a quadrilateral, the sum of all the angles of a trapezium will be 360°.
The following are a few real-life examples of trapezium.


ABCD and PQRS are two trapeziums. What is the difference between the two?
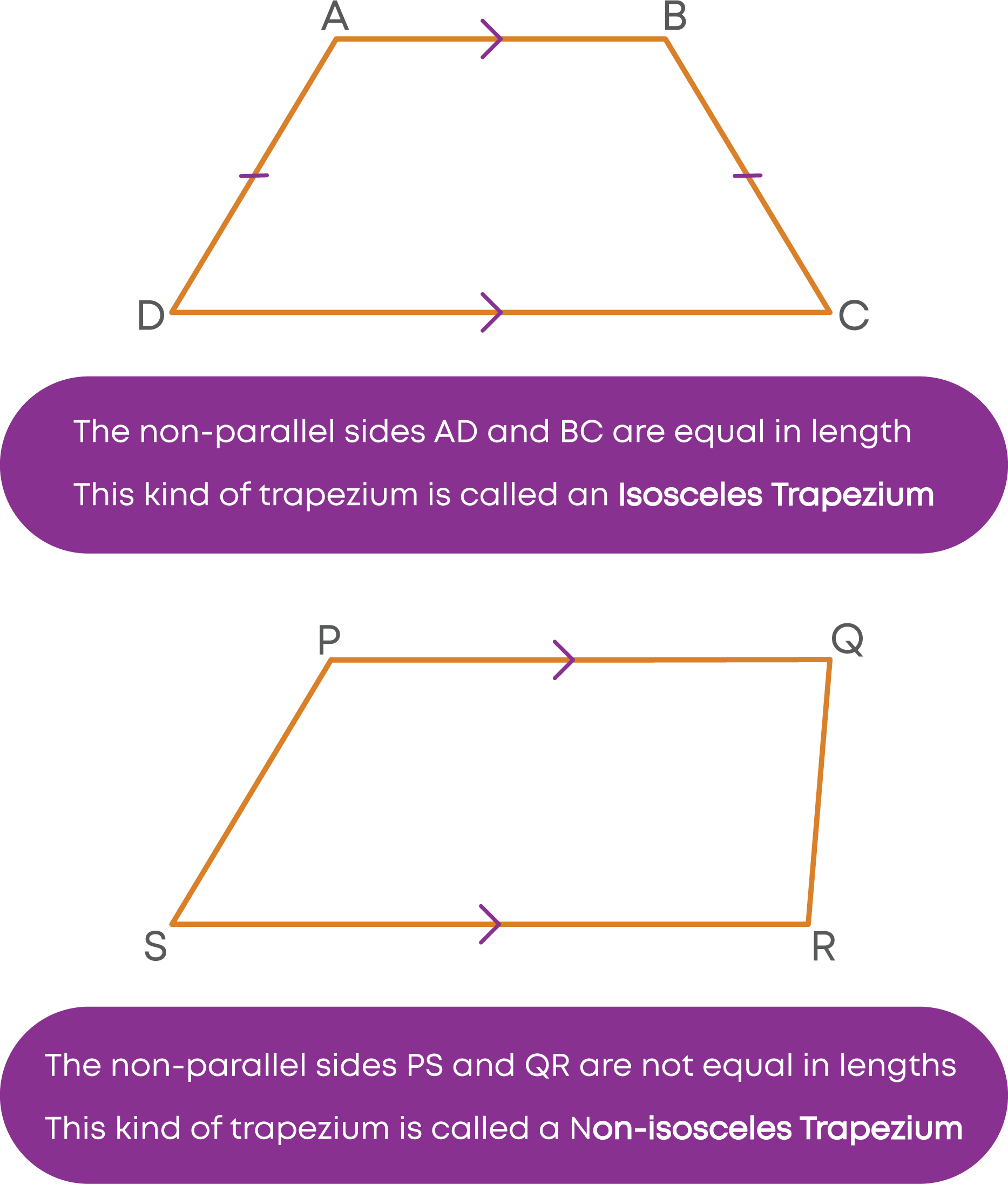
What about the angles of an isosceles trapezium?
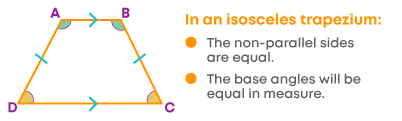
We can summarise the properties of a trapezium as follows:

Since it is a quadrilateral, the sum of all the angles of a trapezium will be 360°.
How do we know that a quadrilateral is a trapezium?

How do we know that a quadrilateral is an isosceles trapezium?

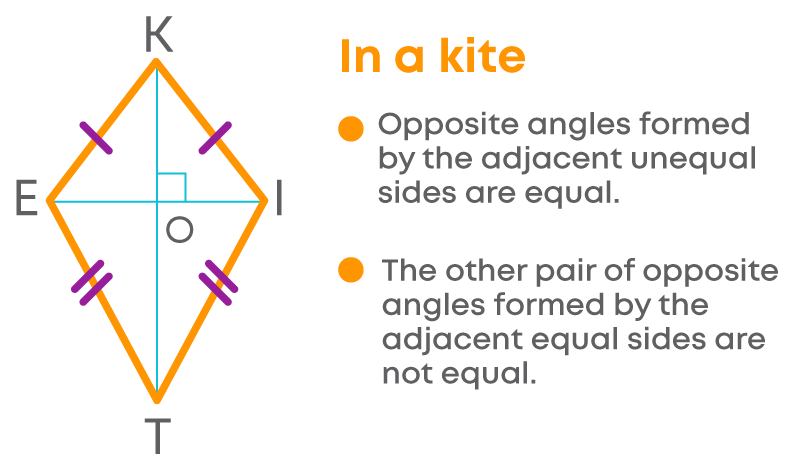
Kite
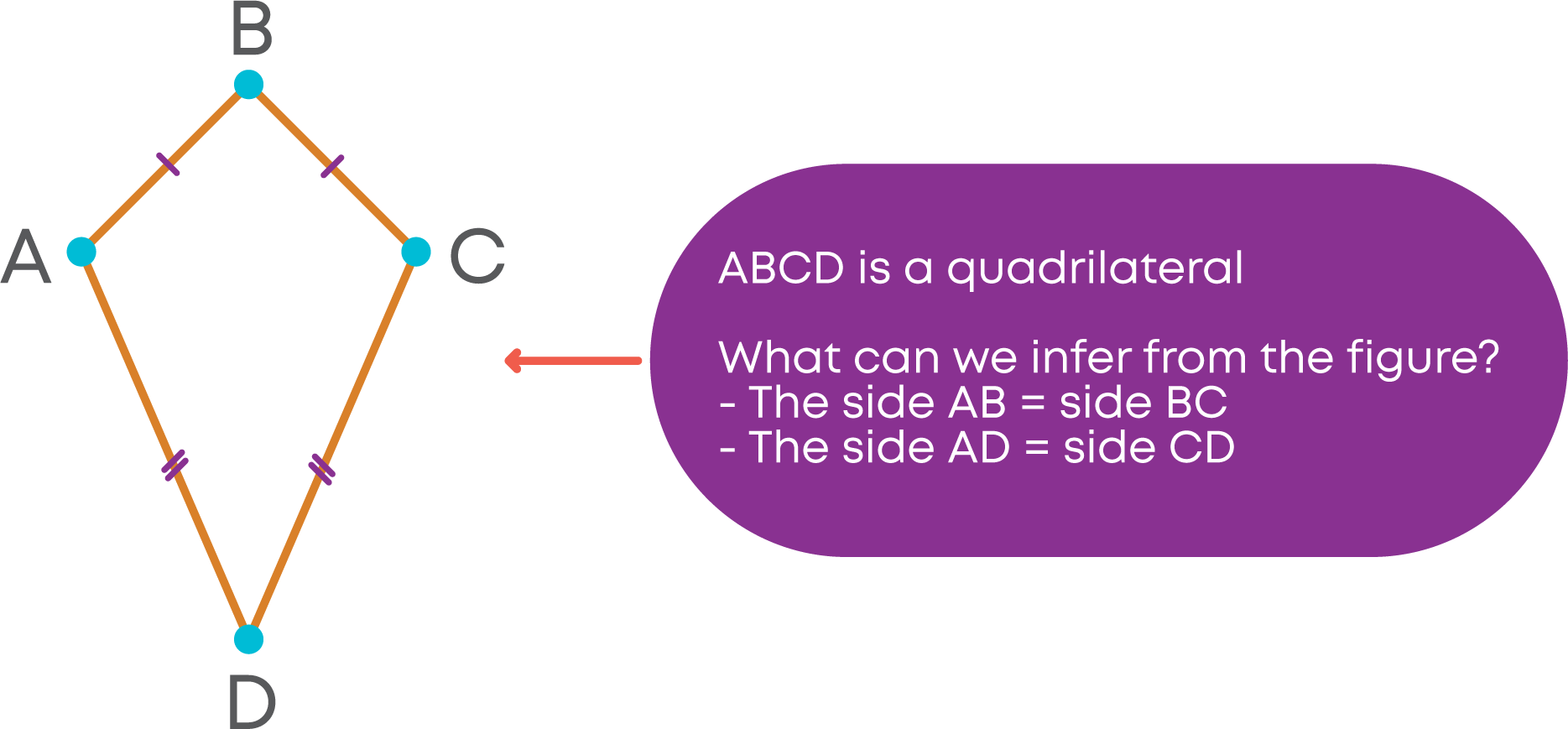
The sides AB and BC are adjacent sides. Similarly, sides AD and CD are adjacent sides.
This type of quadrilateral is called a kite.
In a kite, the longest diagonal divides the kite into two triangles which are congruent.
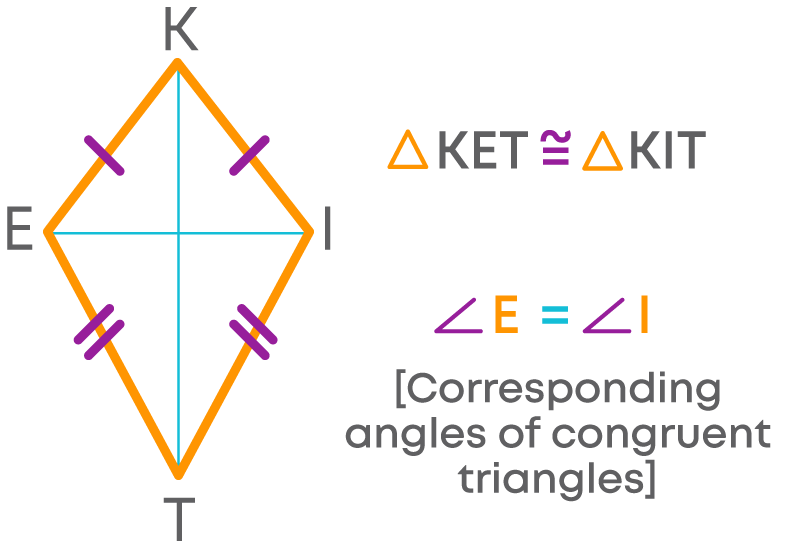
- The angles formed by each pair of unequal adjacent sides will be the corresponding angles and will be equal.
- The shorter diagonal does not divide the kite into congruent triangles.
This means that the other pair of opposite angles are not equal.
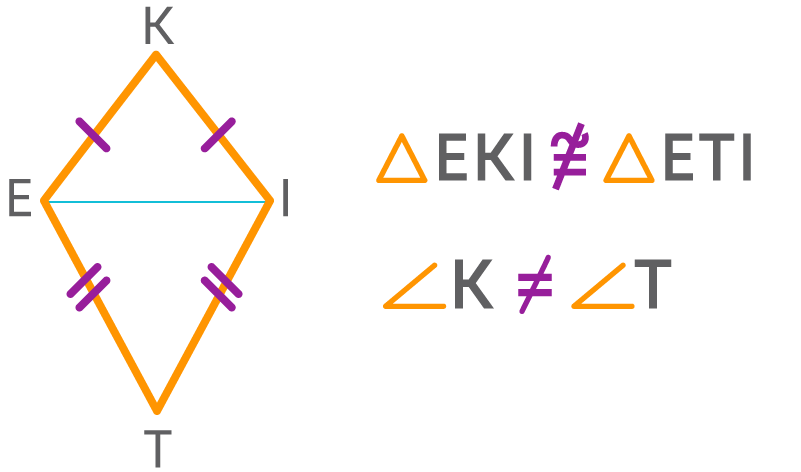
By this, we can say that a kite has one pair of opposite angles equal.



How can we say this? A square or a rhombus has each pair of adjacent sides equal. Hence, we can say that square and a rhombus can be a kite also.

The adjacent sides of a rectangle are not equal. Hence, it cannot be a kite.
So, a kite is a quadrilateral with the following properties
- Two distinct pairs of adjacent sides are equal.
- One pair of opposite angles are equal (Angles formed by the unequal adjacent sides).
- The diagonals meet each other at 90°.
How can we say that a quadrilateral is a kite? A quadrilateral is a kite if:

Parallelogram
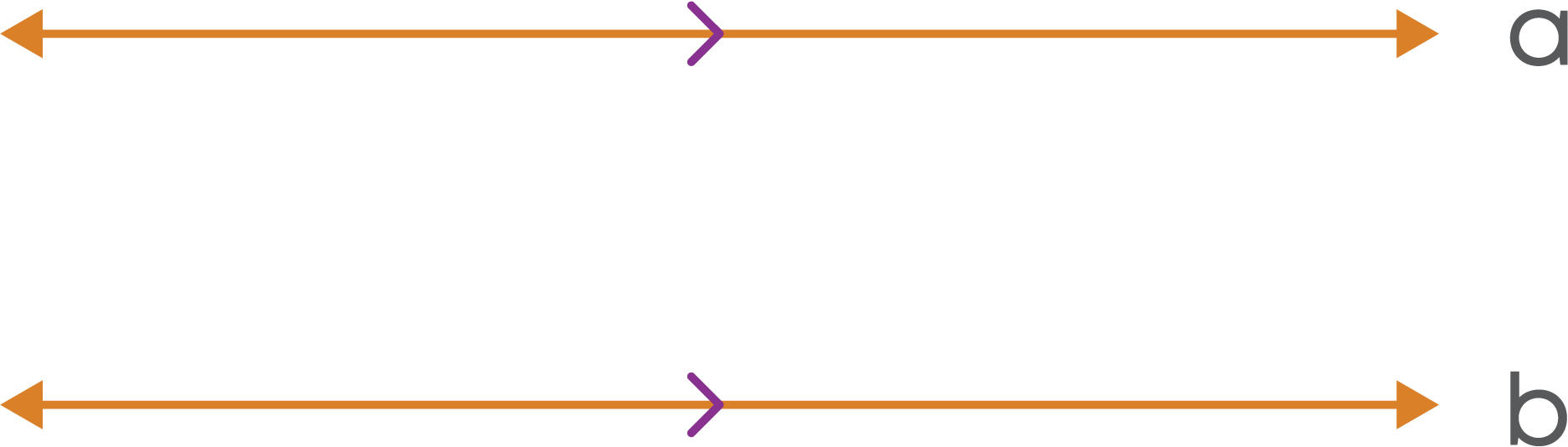
Let us consider two parallel lines ‘a’ and ‘b’.
Two lines ‘x’ and ‘y’ are drawn intersecting these parallel lines.
‘x’ and ‘y’ are also parallel to each other.
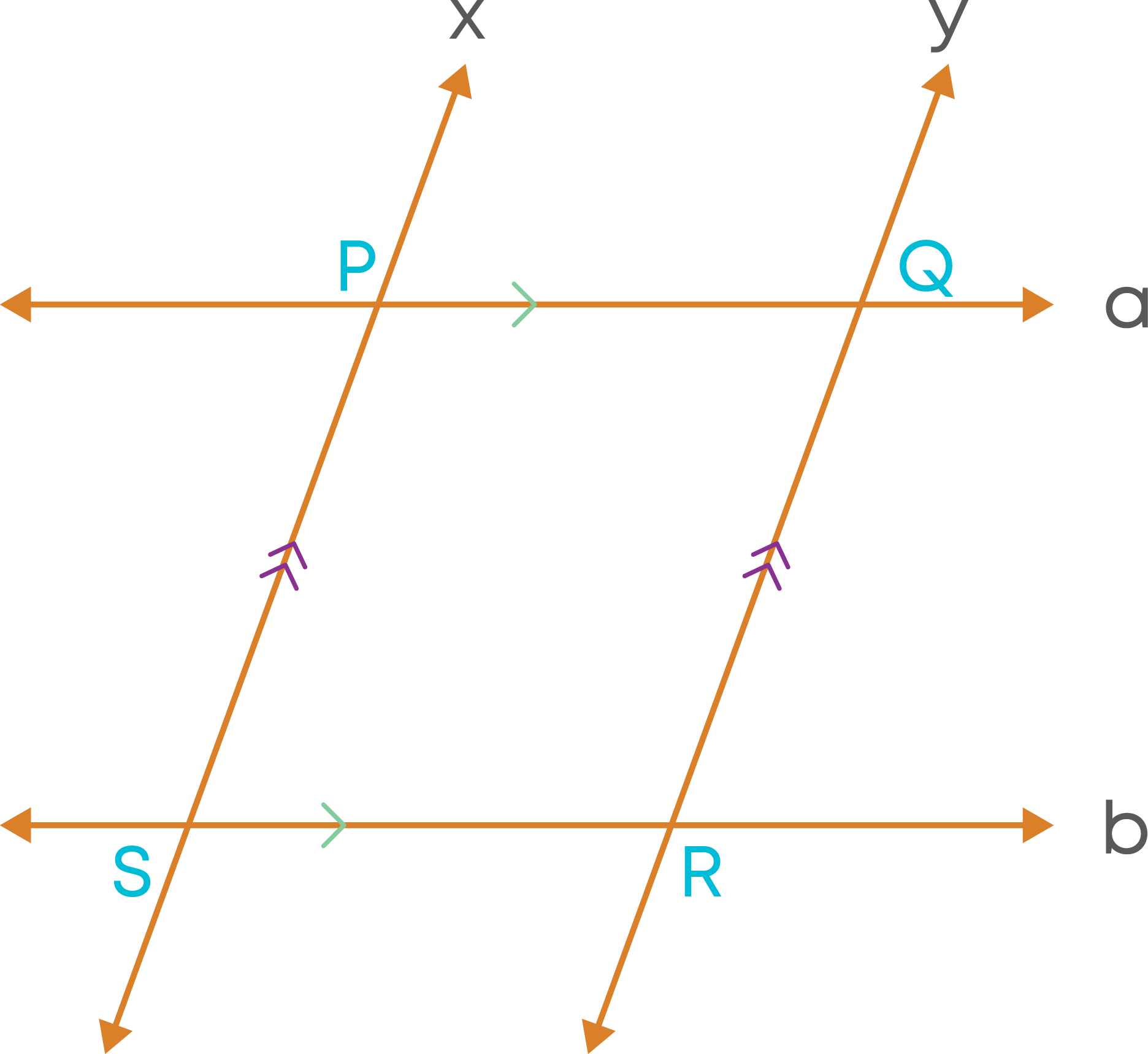
The shape PQRS is a quadrilateral in which,
- The pair of opposite sides are parallel.
- The pair of opposite sides are equal.
Such a quadrilateral is called a parallelogram.
Here are a few examples of parallelograms we see in our daily life.

A parallelogram is a quadrilateral with:
- Pair of opposite sides parallel and equal.
- Pair of opposite angles equal.
- Pair of adjacent angles supplementary.
- Diagonals bisecting each other.
A quadrilateral is a parallelogram,

When we must find the lengths of the sides of a parallelogram given the lengths of adjacent sides, we apply the following property:
- The opposite sides of a parallelogram are equal.
Example:
In a parallelogram ABCD, AB = 6 cm and AD = 4.5 cm. We can find the lengths of the other two sides BC and CD as given below:
Opposite sides of a parallelogram are equal.
Hence, AB = CD = 6 cm
AD = BC = 4.5 cm
To find the lengths of the diagonals of a parallelogram, we apply the following property:
- The diagonals of a parallelogram bisect each other.
Example:
In the parallelogram PARL, the diagonals PR and AL bisect at O.
PO = 5.2 cm and OL = 4 cm
What will be the lengths of the diagonals? It is given that the diagonals PR and AL bisect each other at O.
This means, PO = OR
and AO = OL.
From this, we have
PO = OR = 5.2 cm
PR = PO + OR
= 5.2 + 5.2
= 5.2 + 5.2
Similarly, AO = OL = 4 cm
AL = AO + OL
= 4 + 4
= 8 cm
To find the unknown angles of a parallelogram, we must apply the following properties of the angles:
- Pair of opposite angles of a parallelogram are equal.
- Pair of adjacent angles are supplementary.
To find the length of the sides of a parallelogram when perimeter and relation between the sides is given, we follow these steps:

To find the length of the sides when perimeter of the parallelogram and the ratio of the sides is given, we follow these steps:

To find the angle when measurement of the adjacent angles are given in algebraic form, we follow these steps:

To find the angle when ratio of the adjacent angles are given, we follow these steps:

What is the meaning of ‘opposite angles?’
Opposite angles are
- Angles that are opposite to each other when two lines intersect.
- Formed at each of the opposite vertices.
Adjacent angles are angles adjacent to another angle which shares the same arm of the other angle.
Rhombus
Do you know what the red shape on the card is known as?

It is usually called a ‘diamond’ while playing cards. But it represents the geometrical shape ‘Rhombus’.
Rhombus is a special parallelogram with all sides equal. A rhombus also has equal opposite angles.
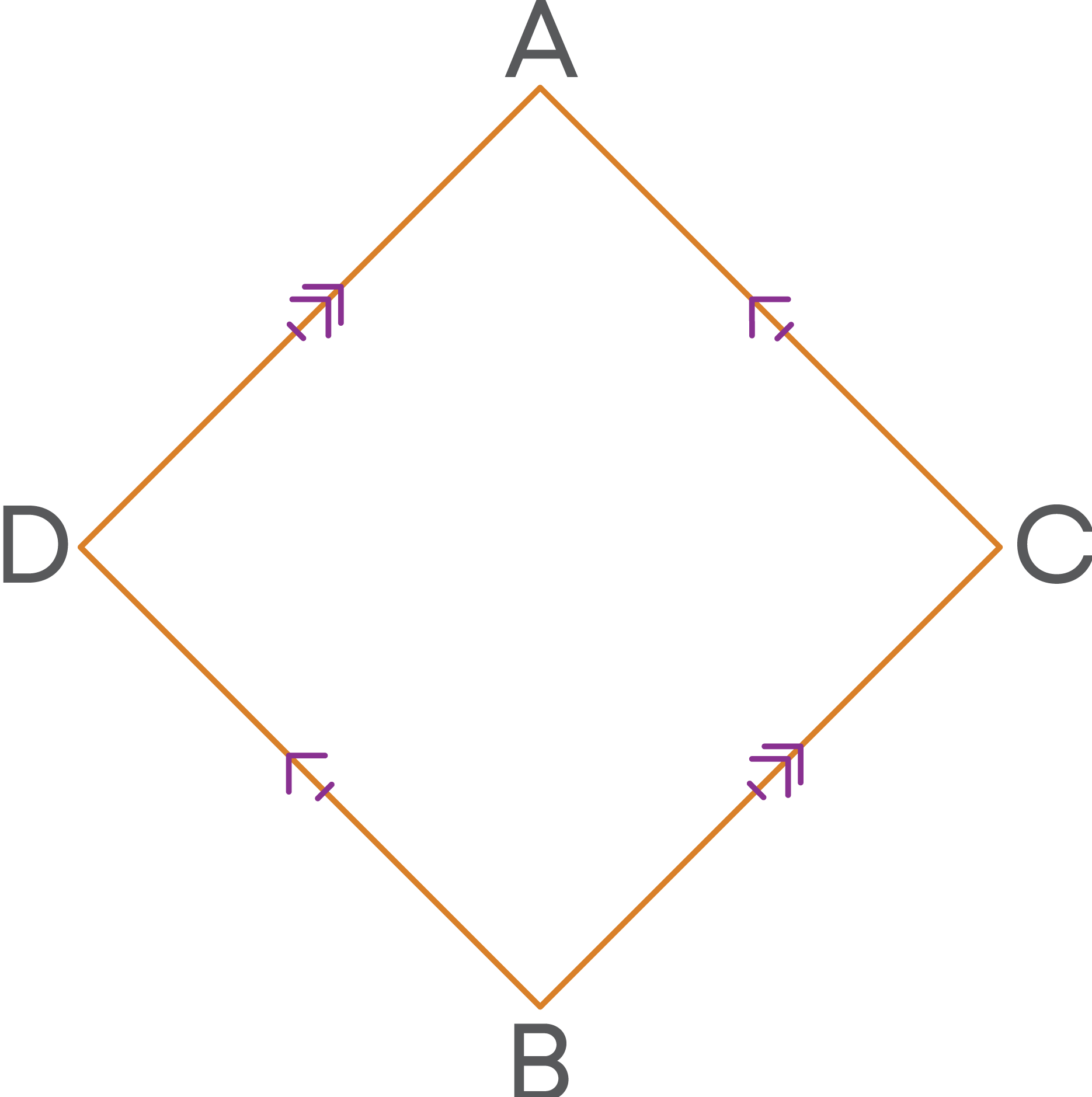
This means that a rhombus has opposite sides parallel. Remember, the diagonals of a rhombus bisect at right angles (90° angle) at their point of intersection.

The diagonals of a rhombus bisect each other perpendicularly.
How can we tell if a quadrilateral is a rhombus?

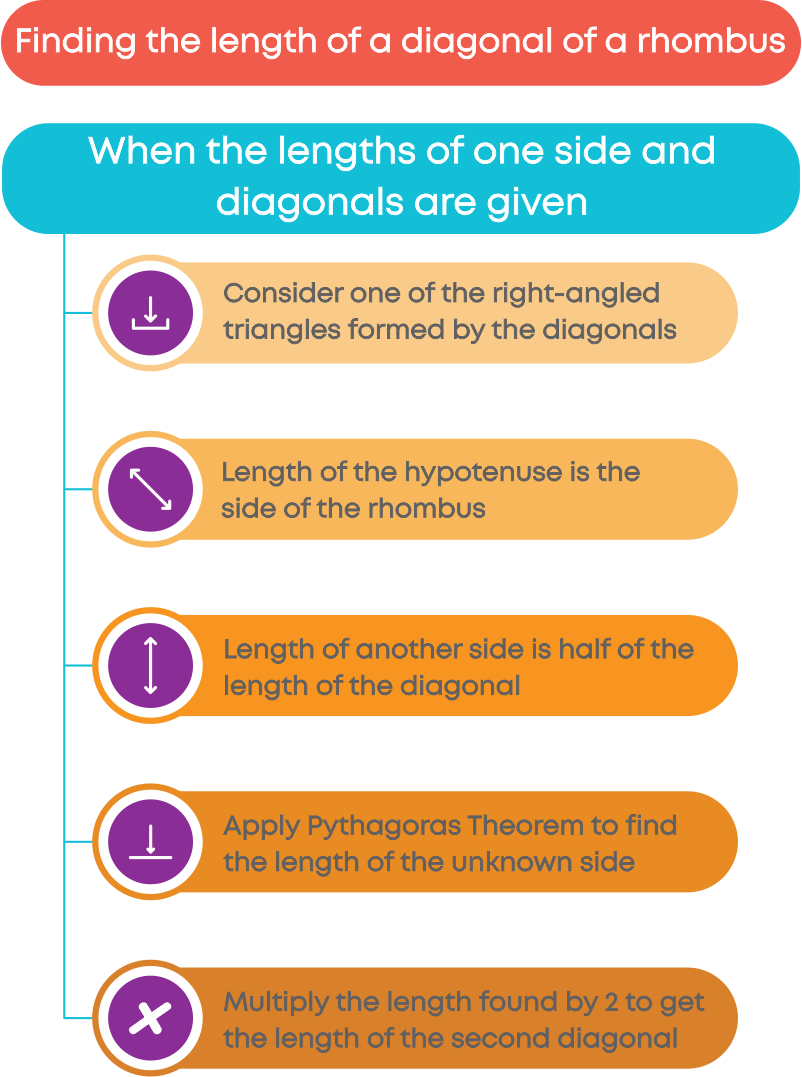
To find the lengths of the sides or diagonals of a rhombus, we apply the following properties:
- All sides of a rhombus are equal.
- The diagonals bisect each other.
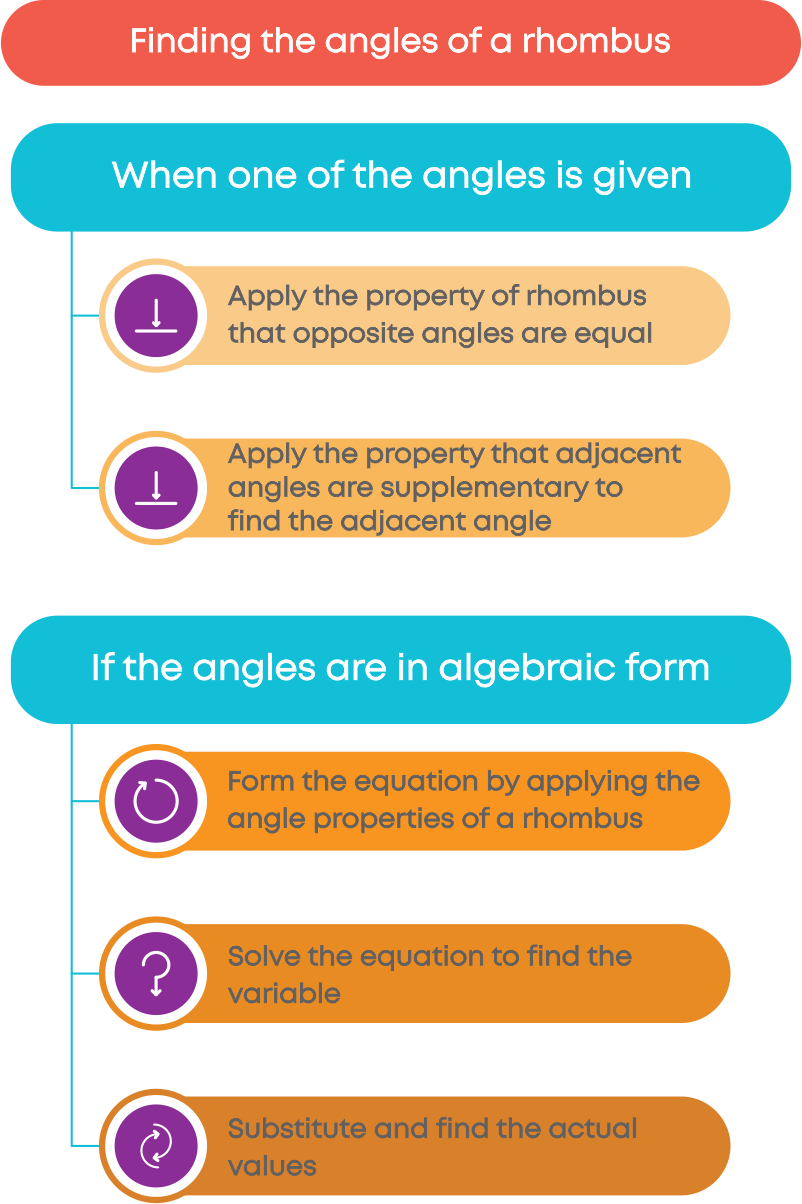
To find the measures of the angles of a rhombus, we apply the following properties:
- Pair of opposite angles are equal.
- Pair of adjacent angles are supplementary.
To find the length of the side of a rhombus when perimeter is given, we follow these steps:

To find the length of the side of a rhombus when length of the diagonal is given, we follow these steps:

Remember:
Rectangle
Consider the set of parallel lines ‘a’ and ‘b’.
Let us draw another set of parallel lines which will be perpendicular to the lines ‘a’ and ‘b’.

- The shape ABCD formed represents a parallelogram.
- The four angles ∠A, ∠B, ∠C and ∠D are all 90°.
The shape ABCD is a rectangle. A rectangle is a parallelogram with the following properties:

A rectangle is a special parallelogram as its diagonals are equal in length.
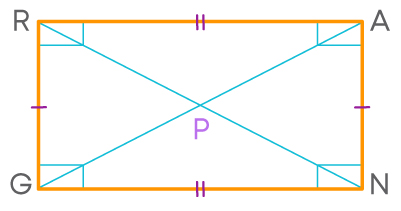
In the rectangle RANG, we can say that
diagonal RN = diagonal AG
To find the lengths of the sides of a rectangle, we apply the following property:
- Pair of opposite sides are equal.
To find the lengths of the diagonals, we apply the following property:
- Diagonals of a rectangle are equal and bisect each other.
Square
A square is a parallelogram with all sides equal and all angles right angles.
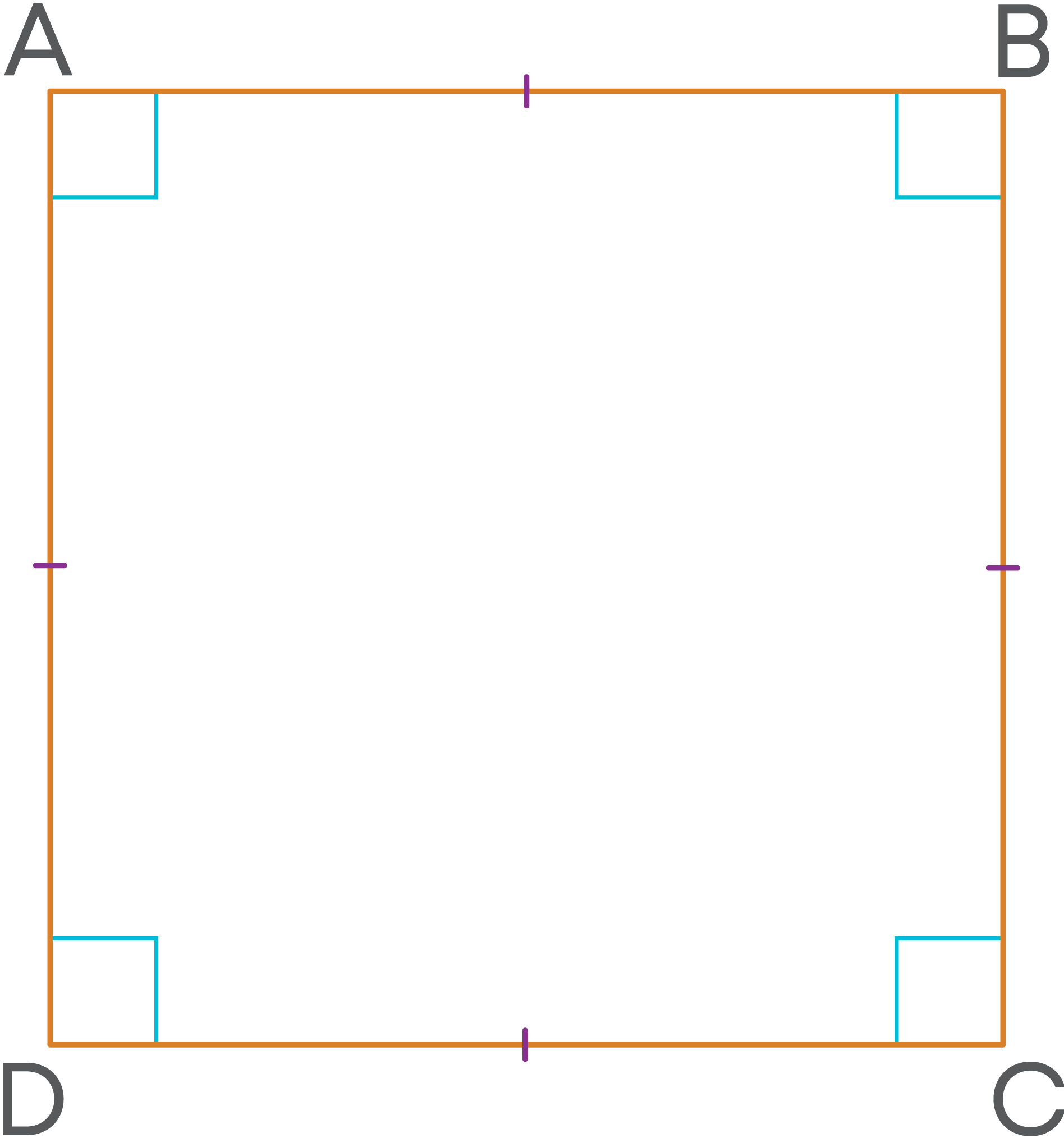
- A square is a special type of parallelogram with all sides equal in length, all angles equal in measure, and all angles as right angles.
- All angles of a square are right angles.
- The diagonals of a square are equal in length.
- The diagonals of a square bisect each other making right angles.
The diagonals of a square:
- Are equal.
- They bisect each other perpendicularly.
In a square:
- When the perimeter is given, we can find the length of the sides by dividing the perimeter by 4.
- We can find the length of the diagonals when the sides are given by applying Pythagoras theorem.
- When the length of a diagonal is given, we can find the lengths of the sides by applying Pythagoras theorem.
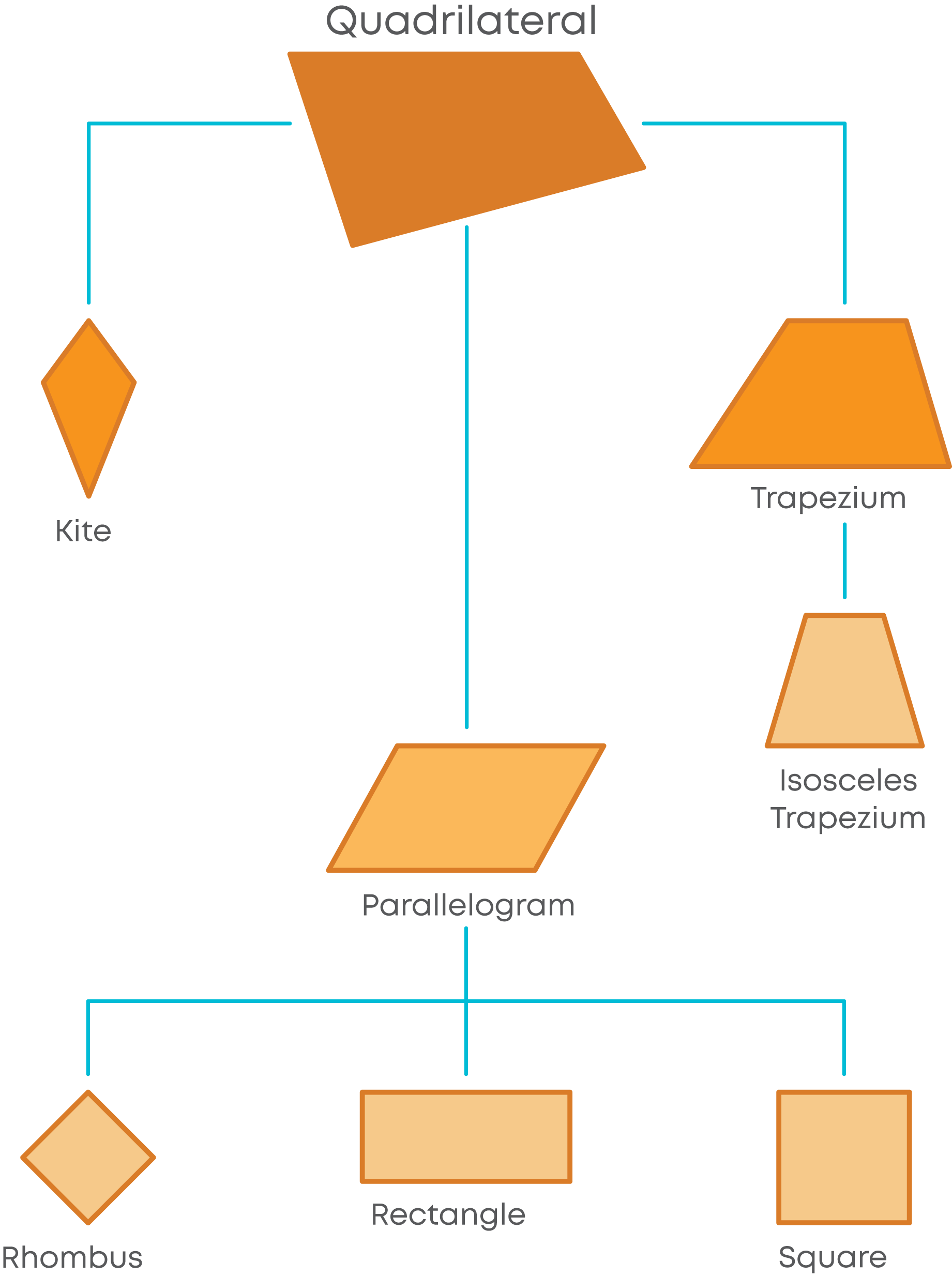
The figure below shows the classification of quadrilaterals.
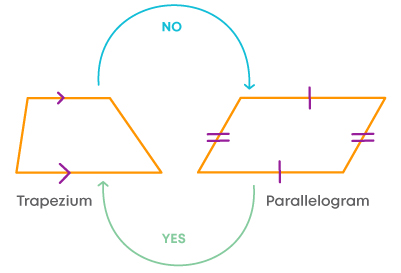
Are the quadrilaterals inter-related? Let us first explore the relation between a trapezium and a parallelogram:
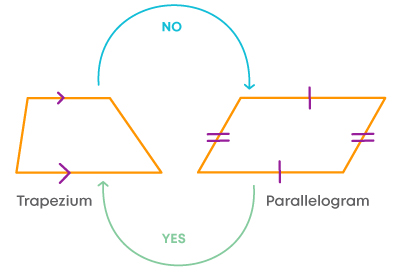
- All parallelograms are trapeziums, as they have at least one pair of opposite sides parallel.
- But a trapezium cannot be a parallelogram as it does not have two pairs of opposite sides parallel and equal.
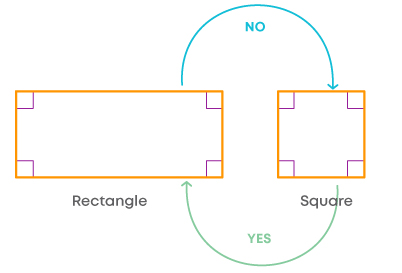
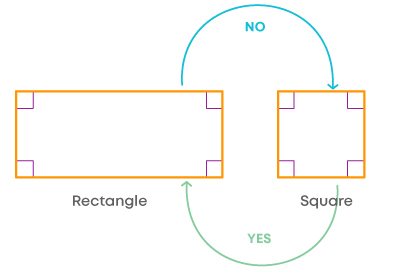
Now, let us see the relation between a rectangle and a square:
- We can consider a square to have a pair of opposite sides parallel and equal.
- All angles of a square are 90°.
- A square can also be a rectangle.
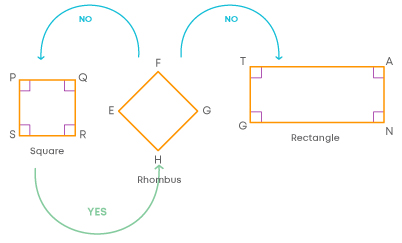
- A rectangle cannot be a square as it does not have all sides equal.
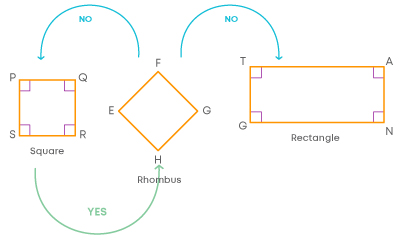
What is the relation between a rhombus and other parallelograms?
- A square can be a rhombus as all its sides are equal and diagonals bisect each other at 90°.
- A rhombus cannot be a square as its angles are not right angles.
- A rhombus cannot be a rectangle and a rectangle cannot be a rhombus.
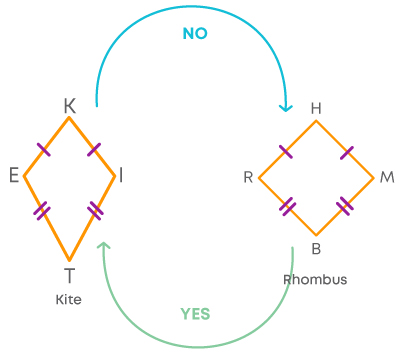
- A rhombus can be a kite as we can consider its adjacent sides to be equal.
Remember:
- If only one pair of opposite sides are parallel, then it is a trapezium.
- If only two pairs of adjacent sides are equal, then it is a kite.
- If opposite sides and angles are equal and the diagonals bisect each other, then it is a parallelogram.
- If all the sides are equal, all angles are 90⁰, diagonals are equal and bisect each other perpendicularly, then it is a square.
- If opposite sides are equal and all angles are 90⁰, then it is a rectangle.
- If all sides are equal and opposite angles are equal, then it is a rhombus.
Common Errors
The following are topics in which students make common mistakes when dealing with polygons and quadrilaterals:
- 1. Finding the exterior angle of a polygon
- 2. Finding the interior angles of a regular polygon
- 3. Finding missing angles in a parallelogram
- 4. Inter-relationship between quadrilaterals
Finding The Exterior Angle Of A Polygon
Remember! The sum of all the exterior angles of a polygon is always 360⁰. To find any missing exterior angle, we must subtract the sum of the remaining angles from 360⁰.
Example:
In the given polygon, we must find two angles, 3x and 4x.
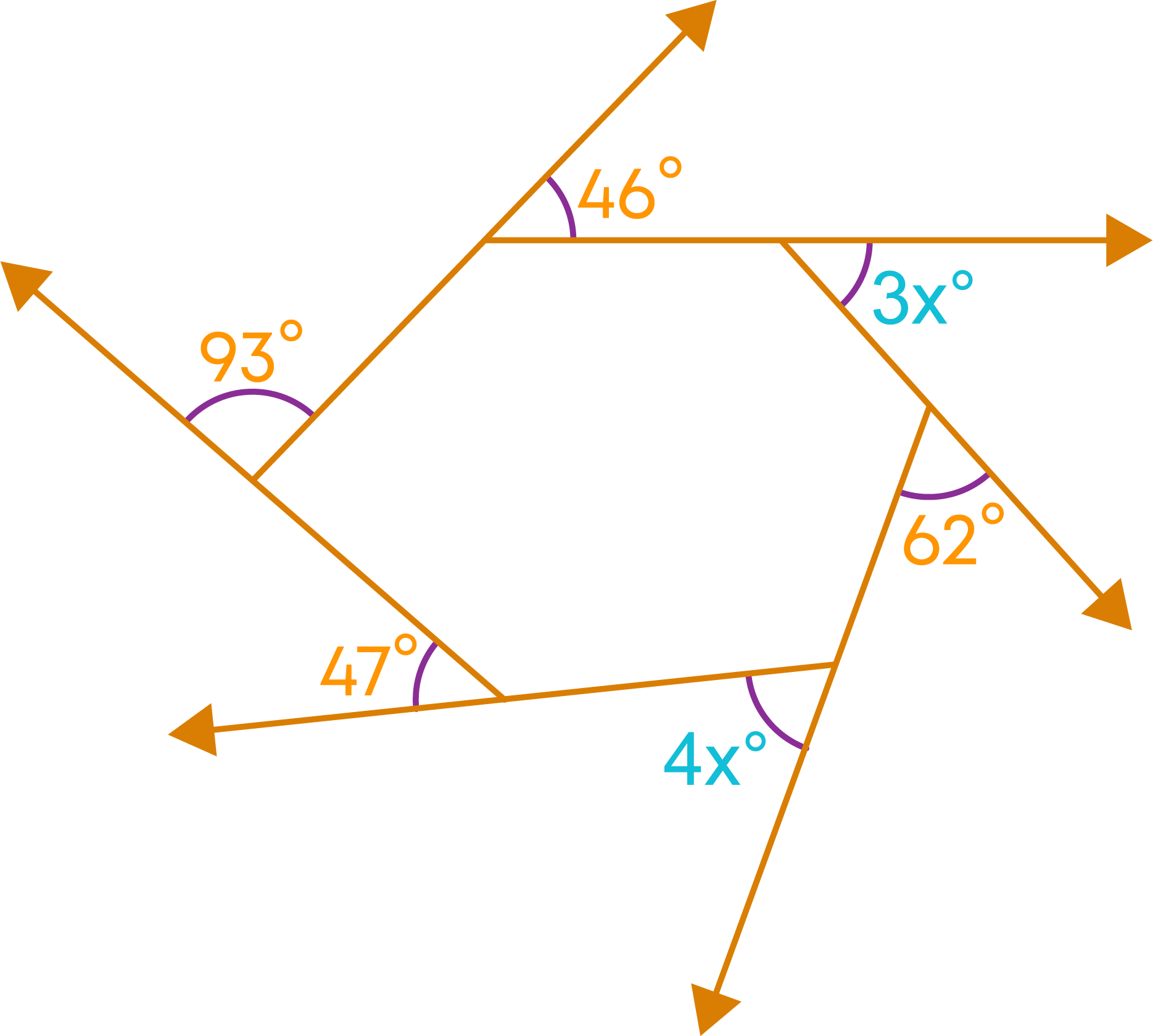
Apply the property:
Sum of the exterior angles of a polygon = 360⁰
4x⁰ + 47⁰ + 93⁰ + 46⁰ + 3x⁰ + 62⁰ = 360⁰
7x⁰ + 248⁰ = 360⁰
7x⁰ = 360 – 248 = 112⁰
x = 112 ÷ 7 = 16⁰
Substitute the value of ‘x’ to find the unknown angles:
3x⁰ = 3 × 16 = 48⁰
4x⁰ = 6 × 16 = 64⁰
Finding The Interior Angles Of A Regular Polygon
To find the sum of the interior angles of a polygon, we use the formula:
(n – 2) × 180⁰ where ‘n’ is the number of sides of the polygon.
Remember to multiply the difference (n – 2) by 180.
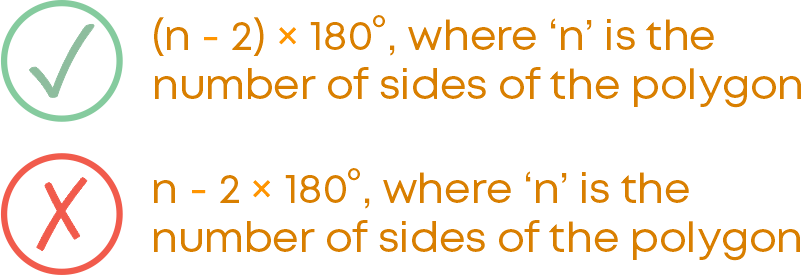
Finding Missing Angles In A Parallelogram
In a parallelogram and rhombus:
- Pair of opposite angles are equal.
- Pair of adjacent sides are supplementary.
Use the properties above to find the measure of unknown angles in a parallelogram or rhombus. In a square or rectangle, all the angles are right angles.
Inter-Relationship Between Quadrilaterals
Different quadrilaterals can have some properties in common. Based on the common properties, we can identify the inter-relation between them. Example:
A parallelogram is also a trapezium. But a trapezium is not a parallelogram.
A rectangle and square, both have opposite sides equal and all angles 90⁰. Hence, a square can also be a rectangle, but a rectangle cannot be a square as all its sides are not equal.
A square can also be a rhombus as all its sides are equal and opposite angles are equal. But a rhombus cannot be a square as its angles are not 90⁰. A rectangle cannot be a rhombus as all its sides are not equal.
Conclusion
Now, can you solve this riddle?
Which of the following polygons will look the same as their mirror image?
a.

b.

c.

d.





















































