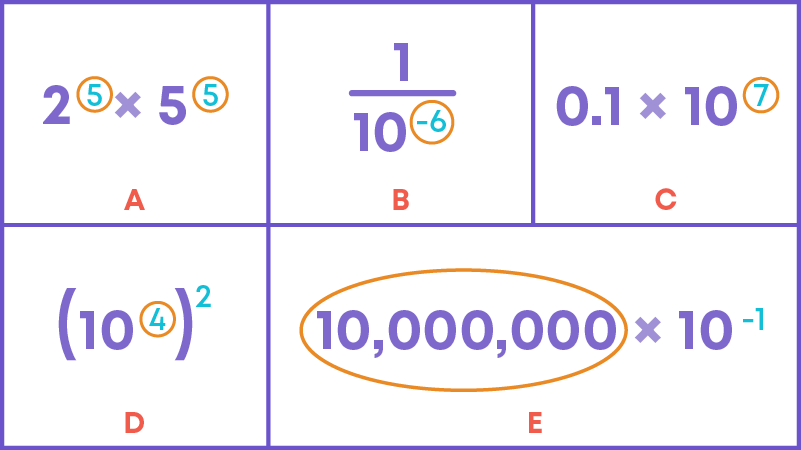Introduction
We work with numbers every day in different fields of life. Some numbers are small, some are large. But there are different applications especially in science where there is a need to work with very small and very large numbers.
For example,
- The diameter of the Milky Way is 200000000000000000000 metre.
- The diameter of a proton is 0.000000000000002 metre.
How do we handle such numbers? Watch the video to know more.
From the video, we understood that we use exponents to write very large and very small numbers. With the use of exponents, very small and very large numbers can be expressed in a manner which is convenient to read, write, compare, and perform a mathematical operation.
We explored distances around us. We found that distances vary in magnitude. Some are very large numbers like the distance between the Earth and the Sun. Some are very small numbers like the radius of the hydrogen atom.
Look at the table below.

Different branches of science study these distances and perform operations with very large and very small numbers. We use exponents to simplify writing and performing operations with such numbers.
We can write 256 as a product of its prime factors. This is nothing but 2 multiplied by itself 8 times. The same can be expressed in exponential form as 28.

- The base is the number that gets multiplied.
- The exponent is the number of times the base is getting multiplied to itself.
A mathematical notation of expressing a quantity as a number raised to the power of another number is called the exponential form or the exponential notation.

Concepts
The chapter ‘Exponents and Powers’ covers the following concepts:
Powers with Negative Exponents
You have learnt in your earlier classes that am means:
- ‘a’ to the power ‘m’
- ‘ a ‘ multiplied by itself ‘m’ times.
Here ‘a’ is called the base and ‘m’ is called the exponent. am is called the exponential form.
Remember:
- Odd powers of negative numbers give a negative result.
- Even powers of negative numbers give a positive result.
Example,
(-2)3 = -8, which is negative
(-2)4 = 16, which is positive
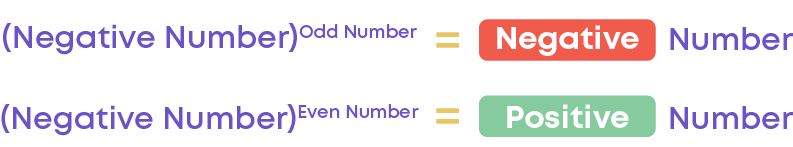
You know how to prime factorise a number. We use the method of prime factorisation to write the given number as a product of its prime factors in exponential form.
Consider the number 432. Let us prime factorise 432.

432 = 2 × 2 × 2 × 2 × 3 × 3 × 3 = 24 × 33
Now, observe the following:
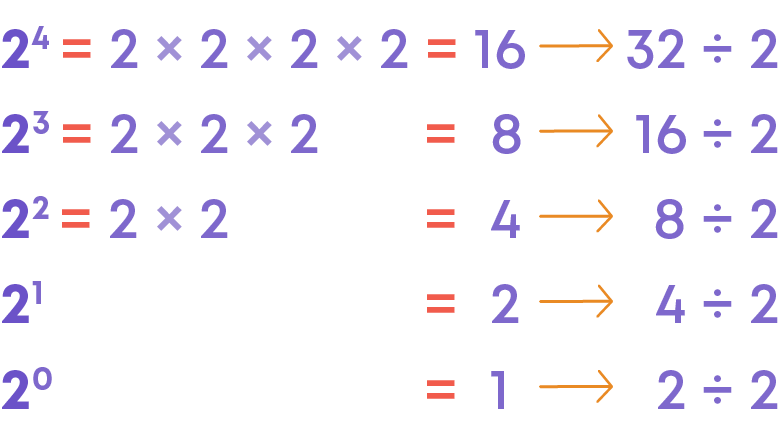
Let us continue the pattern above.
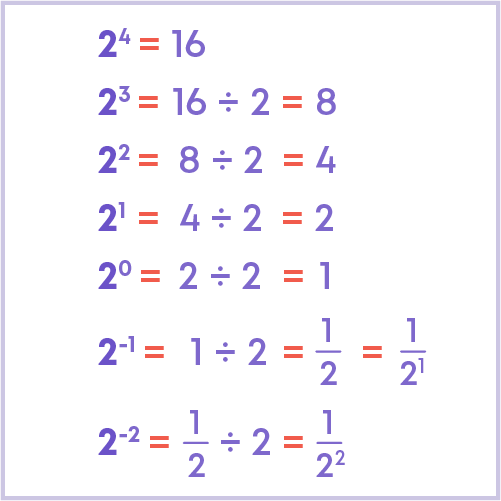
So,
x-m = 1 xm
where x is any non-zero integer and m is a positive integer.
We can also say that,
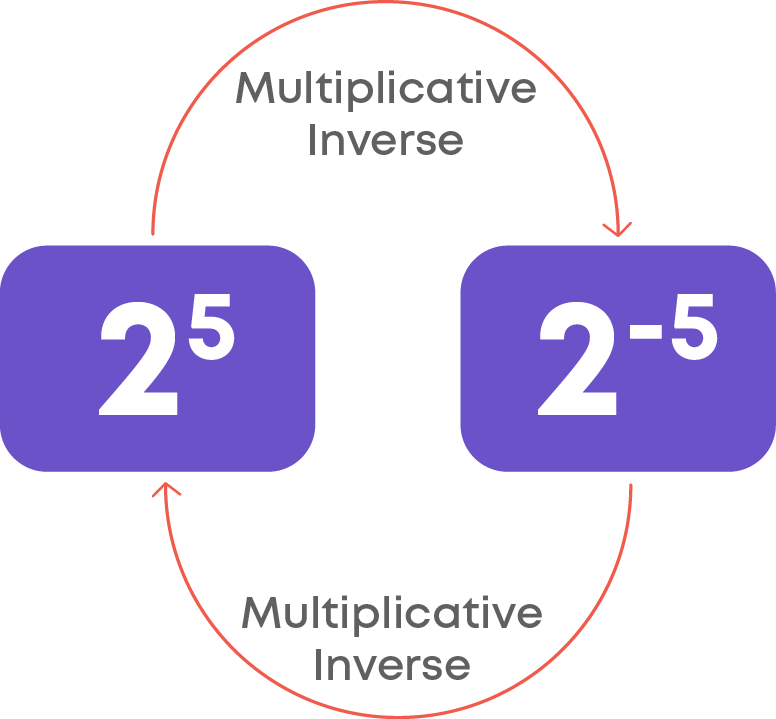
- x-m is the reciprocal or multiplicative inverse of xm
- xm is the reciprocal or multiplicative inverse of x-m
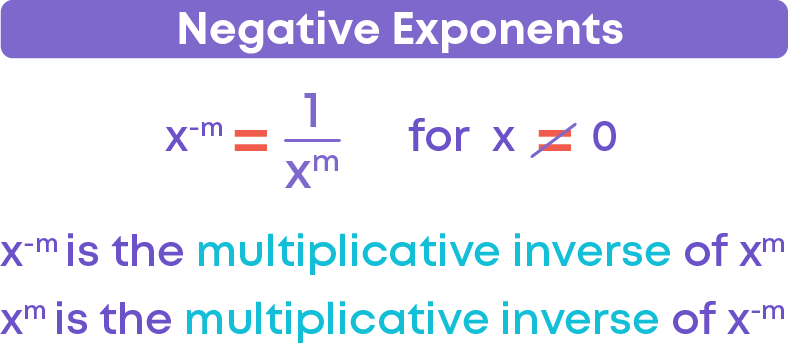
For example,
In science, we deal with very large and very small numbers. For example,
- One gram of hydrogen contains 602,000,000,000,000,000,000,000 atoms.
- Radius of a hydrogen atom is 0.000000000025 metre.

We use positive exponents to write very large numbers. In the same manner, we use negative exponents to write very small numbers.
You know how to evaluate powers with positive exponents. For example, to find (-2)5 we multiply (-2) by itself 5 times.
Let us evaluate 2-5
Step 1 : Convert the negative exponent to positive exponent.
We know that x-m = 1 xm
So, 2-5 = 1 25
Step 2 : Evaluate the expression by repeated multiplication.

Hence, 2-5 = 1 32
Now, consider the decimal number 123.456. Its expanded form is:
123.456 = 1 × 100 + 2 × 10 + 3 × 1 + 4 × 1 10 + 5 × 1 100 + 6 × 1 1000
= 1 × 102 + 2 × 101 + 3 × 100 + 4 × 1 101 + 5 × 1 102 + 6 × 1 103
Since x-m = 1 xm

Laws of Exponents
Laws of exponents hold good even if exponents are negative.

Now, let us simplify (64 ÷ 6-5)3 × 6-3
Let us observe the expression and identify the laws that are to be used to simplify it.
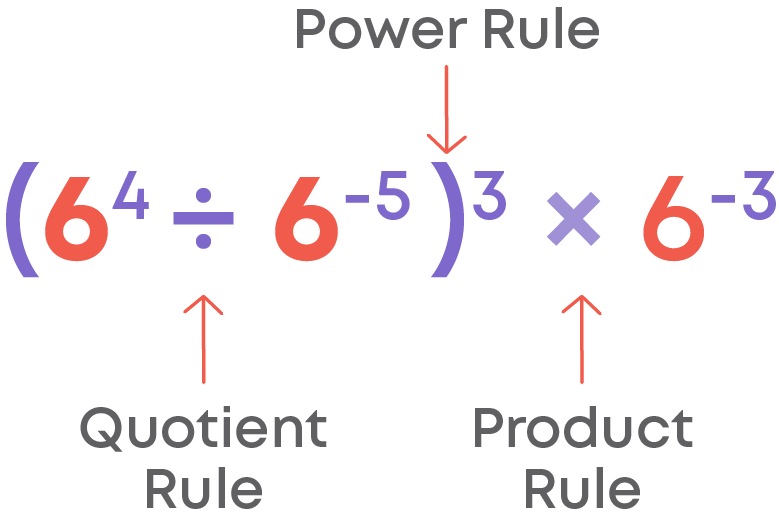
Let us apply these rules.
(64 ÷ 6-5)3 × 6-3
= (64 – (-5))3 × 6-3
= 69 × 3 × 6 -3
= 627 × 6-3
= 627 + (-3)
= 624
Now consider this equation.
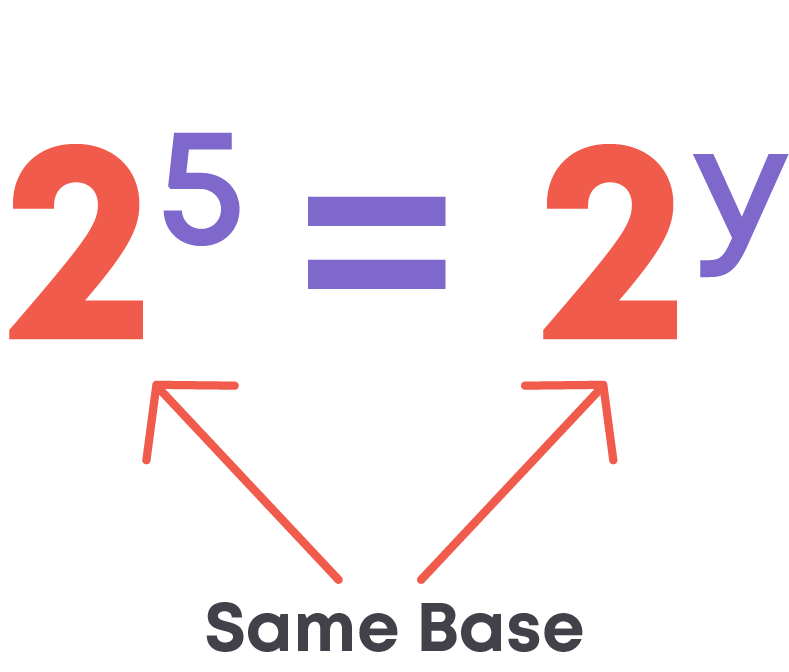
We can see that the LHS and RHS are exponential numbers raised to the same base. So, we can say that y = 5.
When two exponential numbers have the same base, then their exponents are equal.
Expressing Very Small and Very Large Numbers in the Standard Form
You can express very large numbers in the standard form. For example:

It is difficult to work with large numbers. Expressing large numbers in standard form simplifies the operations performed on them like comparing, adding, subtracting, etc.
Can we write small numbers in the standard form? We use negative exponents to write very small numbers in the standard form. For example,
Pollen grains cause allergies in many people, but they usually are too small to see. A pollen grain is approximately, only 0.00002 meters in diameter. How is this number written in the standard notation?
0.00002 = 2 100000 = 2 105 = 2 × 10-5
The diameter of a pollen grain written in the standard form is 2 × 10-5m.
Let us now understand how to write the number in the standard form back to its usual form.
The size of a plant cell is 1.275 × 10-5 metres. Let us write in the numerical (usual) form.
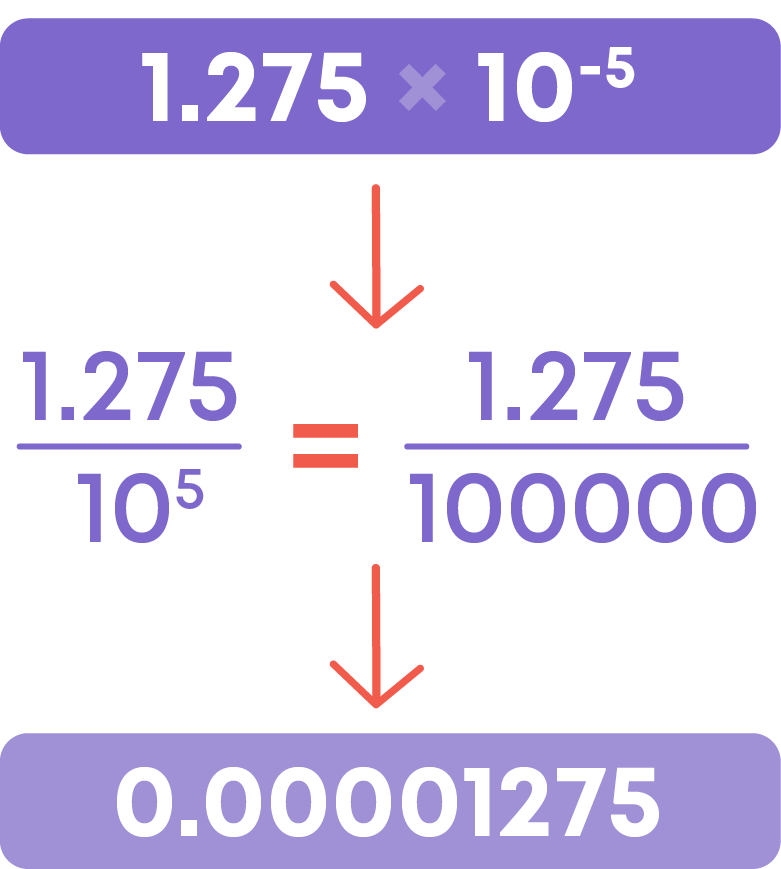
Hence, the size of a plant cell is 0.00001275 metre.
You know how to compare two numbers. Let us now understand how to compare numbers written in the standard form.
Compare 7.5 × 105 and 2.5 × 107

The number with the smaller exponent is smaller. Hence, 7.5 × 105 < 2.5 × 107
Compare 7.5 × 10-5 and 2.5 × 10-7
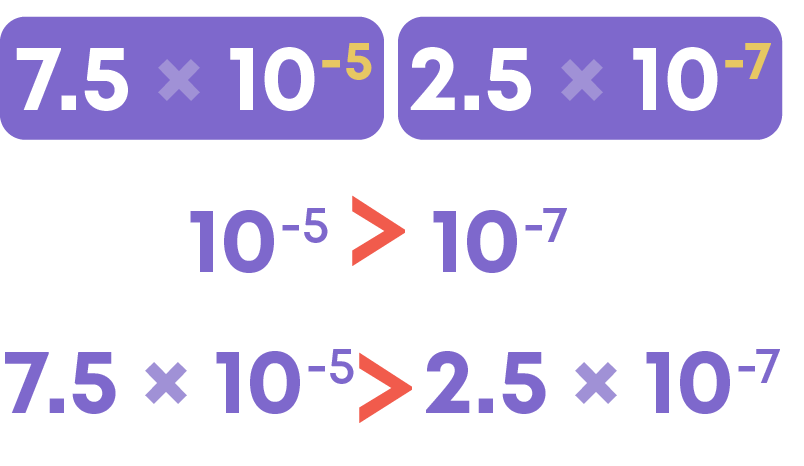
The number with the greater exponent is the greater.
Compare 7.5 × 10-5 and 2.5 × 10-5
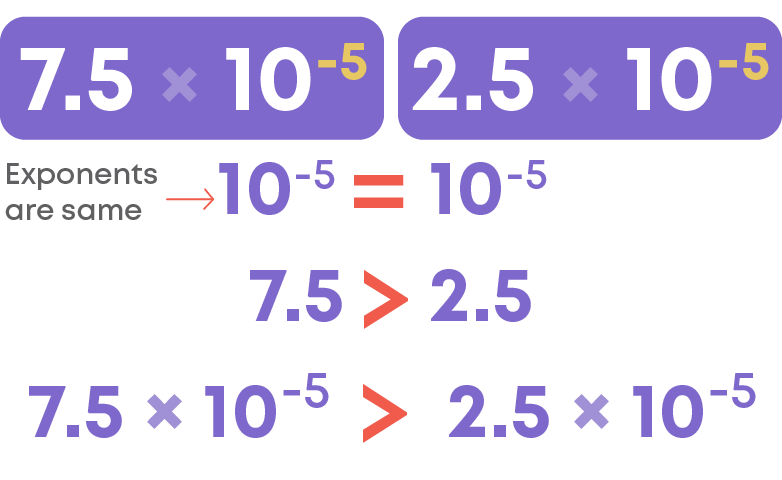
Both the numbers have the same exponent, observe the decimal number part. We can see that 7.5 > 2.5
Common Errors
The following are topics in which students make common mistakes when dealing with exponents and powers:
- 1. -32 is not the same as (-3)2
- 2. 5-2 is not the same as -52
- 3. The standard form of small numbers
- 4. 2 × 10-5 + 3 × 10-7 is not 5 × 10-12
-32 Is Not The Same As (-3)2
The expression -32 means to multiply two 3's together first (by order of operations), and then take the negative of that answer.
-32 = -(32) = -(3 × 3) = -(9) = -9
The expression (-3)2 means to multiply two (-3)'s together.
(-3)2 = (-3) × (-3) = 9
5-2 Is Not The Same As -52
52 means multiplication by 5 two times.
52 = 5 × 5 = 25
In the same manner, 5-2 means division by 5 two times.
5-2 = ( 1 5 )2
The Standard Form Of Small Numbers
How will you express 8000000000 in the standard form? The given number is 8 followed by 9 zeroes.
Hence, the standard form is 8 × 109.
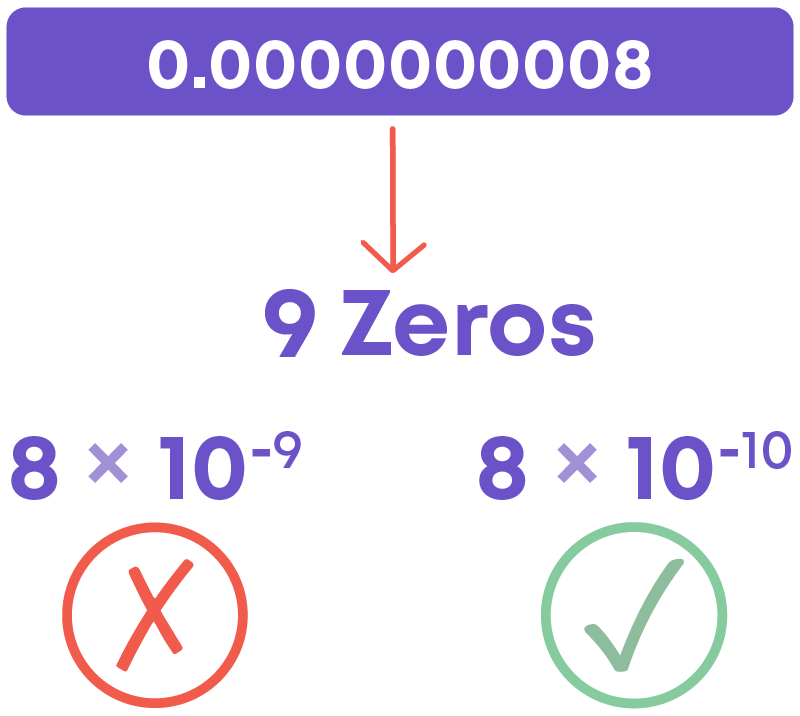
Consider 0.0000000008. What is its standard form?
8 is preceded by 9 zeroes. But its standard form is not 8 × 10-9.
The standard form of 0.0000000008 is 8 × 10-10.
2 × 10-5 + 3 × 10-7 Is Not 5 × 10-12
How do you add two numbers expressed in the standard form? To add or subtract two numbers in the standard form, make sure that they are written with the same power of 10.
2 × 10-5 + 3 × 10-7
= 2 × 10-5 + 0.03 × 102 × 10-7
= 2 × 10-5 + 0.03 × 10-5
= 2.03 × 10-5
Conclusion
Exponents and powers are useful in our daily lives. Can you solve this riddle based on exponents and powers?
Which of the following options show 1 million?