Introduction
We have been learning about different concepts of geometry. But do you know the history behind geometry? Let us watch this video to learn the history of geometry. Also, in this video, we will learn what Euclidean geometry is.
Euclid introduced the method of proving mathematical results by using deductive logical reasoning and the previously proved results. His famous book “The Elements” contains wonderful results on geometry.
- Euclidean geometry is also known as the geometry of plane figures.
- Euclid described different terms of geometry such as point, line, surface etc., in his book “The Elements”.
- Also, Euclidean geometry is the basis for most of the geometry studied in schools.
Hence, it is important and interesting to learn Euclidean geometry.
Concepts
The chapter ‘Introduction to Euclid's Geometry’ covers the following concepts:
Euclidean Definitions of Geometrical Terms
Can you mark a dot on a paper using a sharp pencil? Does it have length and breadth? Examine the dot marked on a paper through a magnifying lens.

How does it look? It looks like a circular disc.
How do the stars appear in a dark sky at night? The stars appear like small, brilliant points of light.

Though the sun is also a star, it looks much bigger than the other stars. Why is it so? This is because the sun is much closer to us than the other stars.
The above experiment and observation lead us to think about the concept of a point.
A point can only be imagined to be a dot on a flat surface known as a plane. For our visualisation, we put a dot and name it using a capital letter. So, in geometry, we say a point has a position but no magnitude, which means that a point has no breadth or length.
Euclid described a point based on this idea. A point is that which has no part.
Now, we know that a point has no length and no breadth, i.e., a point is dimensionless. Note that a ‘dimension’ is the measure of the size in one direction. In other words, it is the measurement of length, breadth, and height. What happens when a point moves?

When a point moves freely as shown above, if we trace its path, we get a curved line. Now, we will see what will happen if a point moves without changing the direction.

The path traced is a straight line. Thus, a line is generated when a point moves. A line has length but no breadth, i.e., a line has one dimension.
If the tip of a pencil is moved over a sheet of paper, the path traced represents a line. But, such a trace, however finely drawn, has some breadth. So, a line can only be imagined to be a path traced by a moving point.
A line is named using two capital letters. Sometimes, lines are also named using single small letters, like ‘m’, ‘l’, ‘n’ etc. A line extends endlessly in both directions. Thus, it does not have an endpoint. The line ‘l’ is shown below.

A line is a breadthless length.
The word ‘segment’ refers to a part. So, a line segment means a part of a line.

The highlighted part of the line ‘l’ is a line segment.
- We can see that it has two fixed endpoints, A and B.
- This can be named as the line segment AB.
- The distance between the points A and B gives the length of the line segment AB. So, a line segment has a definite length.
If a part of a line has only one endpoint, is it called a line segment? No. Consider the example below:

- P is a point on the line XY.
- The highlighted part of the line XY has the point P as its endpoint as it does not go beyond the point P. Also, it extends endlessly on the other side.
Such a part of the line is called a ray.
- Here, we can name the part of the line as the ray PY.
- This can be visualised as starting from the point P and extending endlessly. So, P can be called its initial point. Thus, a ray has one endpoint which can be called its initial point.
- Since a ray extends endlessly in one direction, it does not have a definite length.
A ray is a part of a line which has one endpoint and extends endlessly on the other side.
We know that when a point moves, we get a line. Now, what do we get when a line moves?

We get a plane surface. A plane surface is a surface which lies evenly with the straight lines on itself.
We know that a line has one dimension. By moving, it generates another dimension. So, a plane surface has two dimensions, length, and breadth.
A surface is that which has length and breadth only.

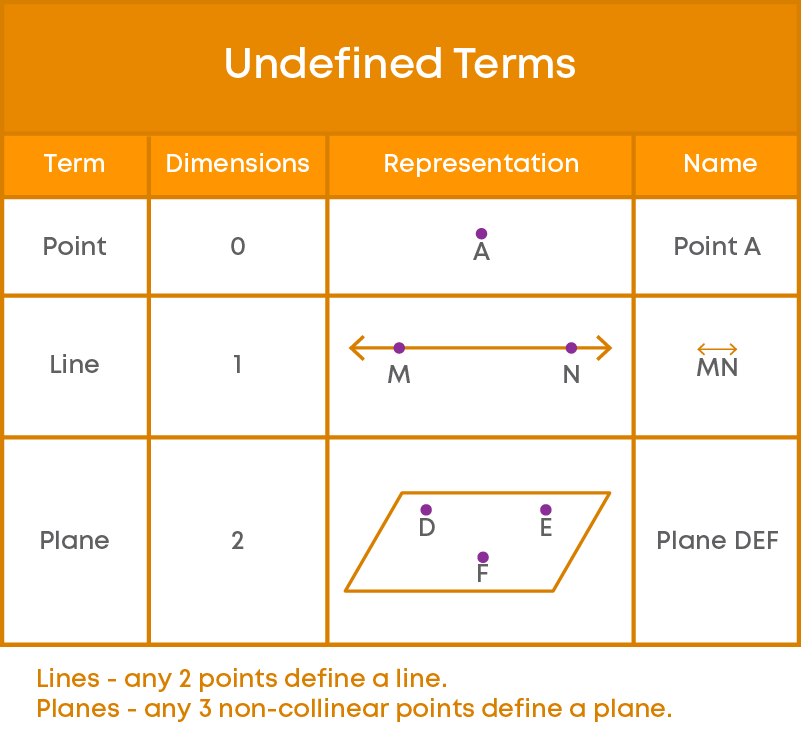
Euclid had defined points, lines, surfaces, and many other things. But, to define one thing, you need to define many other things. E.g., Euclid has defined a point as that which has no part. Here, what is ‘part’?
It needs to be defined. If we define it as that which occupies some area, then ‘area’ must be defined. Thus, you may get a long chain of definitions without an end. For such reasons, mathematicians leave some geometrical terms undefined. That is why, even though Euclid has described a point, a line, a surface, etc, they are considered to be undefined terms in mathematics.
Euclid’s Axioms
We have already seen how Euclid described points, lines, and surfaces. These definitions or ideas may be made into a systematic science. Euclid sorted out the structure of Euclidean geometry as shown below:

The reasons which we use will, in some cases, depend on the facts which have been proved already, in some cases on the definitions and in some other cases on self-evident truths.
These self-evident truths cannot have a reason further. For example,

This statement is a self-evident truth. We accept it to be true without any proof. These self-evident truths are called axioms.

e.g., while solving some equations or creating an equation having a given solution, we use balancing method. To solve the equation x – 5 = 7, we add 5 on both sides of the equation.
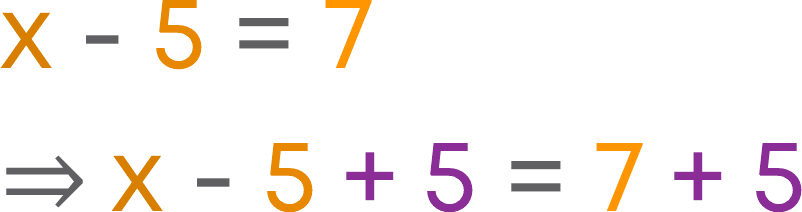
Here, the equation says ‘x – 5’ and ‘7’ are equal. In the first step of solving, we add 5 to ‘x – 5’ and ‘7’.
Also, we say that they are equal. To achieve this step, we are accepting the fact that when equals are added to equals, the results are also equal. We do not find any reason or proof for this fact. This is a self-evident truth.
Euclid used axioms while proving results in geometry. Let us discuss these axioms now.
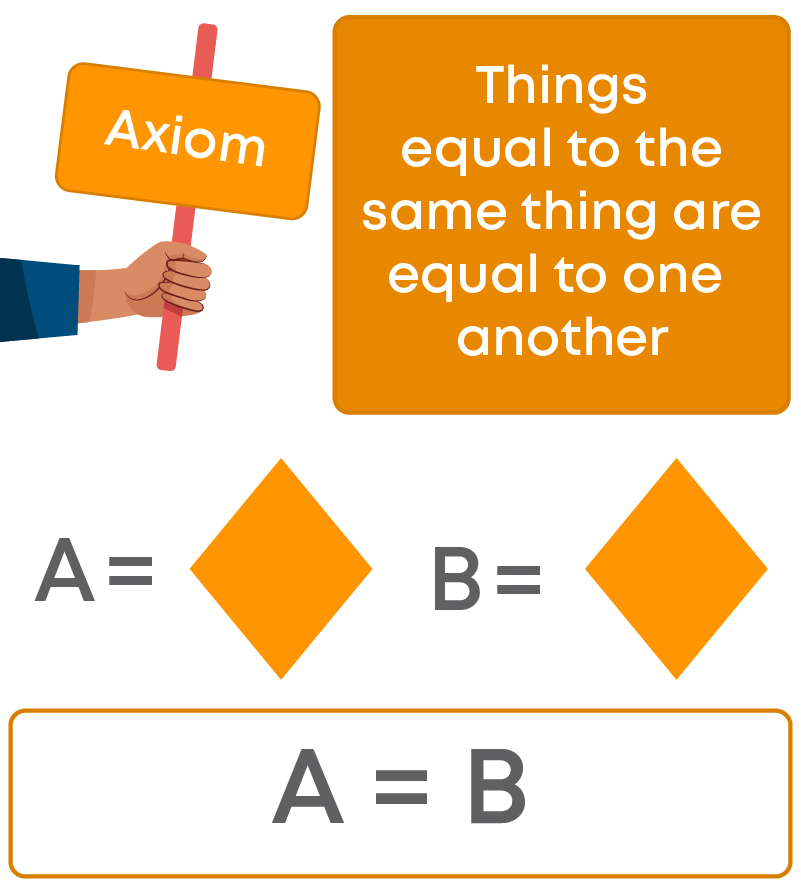
Things Equal To The Same Thing Are Equal To One Another
Suppose bars of chocolates of two brands cost ₹10 each.

Can we say that the cost of the chocolate of one brand is equal to the cost of the chocolate of the other brand? Yes, both the chocolates cost the same amount, i.e., the cost of the chocolate of one brand is equal to the cost of the chocolate of the other brand.

Thus, here two quantities equal to ₹10 are equal. In general, we can say that the quantities equal to the same quantity are equal.
Euclid stated this fact in the form of an axiom as “Things equal to the same thing are equal”.
This axiom is used to prove many results in geometry as well as in other branches of mathematics.
If Equals Are Added To Equals, The Wholes Are Equal
If equal quantities are added to equal quantities, the resulting quantities are also equal.

This axiom is used to prove many results in geometry as well as in other branches of mathematics.
If Equals Are Subtracted From Equals, The Remainders Are Equal
Mathematically, this axiom can be represented as:
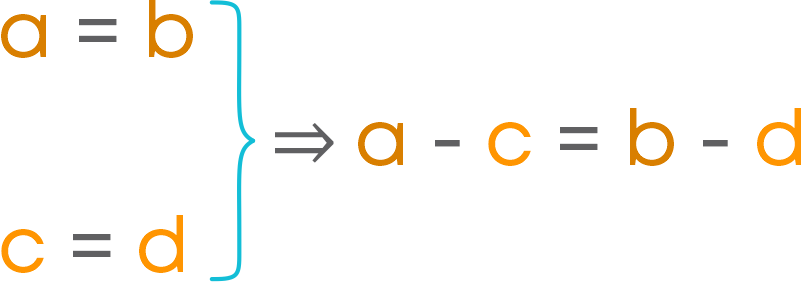
Let us learn how the axiom “If equals are subtracted from equals, the remainders are equal” is used in algebra. Consider the equation 2x + 7 = 12.
Let us use the axiom to show 2x = 5.
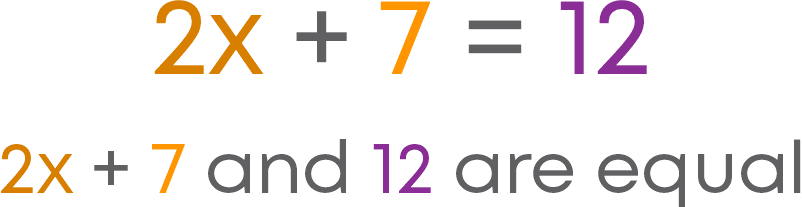
To get 2x on the LHS, we subtract 7 from 2x + 7. Here, 2x + 7 and 12 are equal. So, we subtract 7 from both, which means we subtract equals from equals. We use the axiom “If equals are subtracted from equals, the remainders are equal”.
So, the results are also equal. Thus, we get,
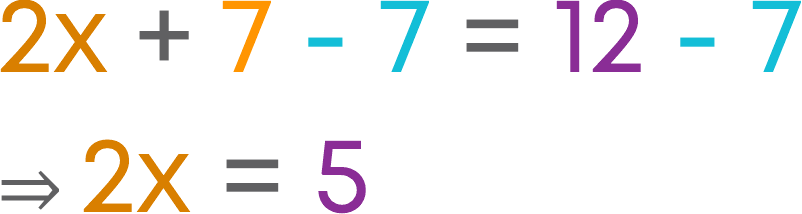
Thus, we can obtain 2x = 5, from the equation 2x + 7 = 12 using the axiom “If equals are subtracted from equals, the remainders are equal”.

Things Which Coincide With One Another Are Equal
Corresponding parts of congruent triangles coincide when triangles are superimposed.
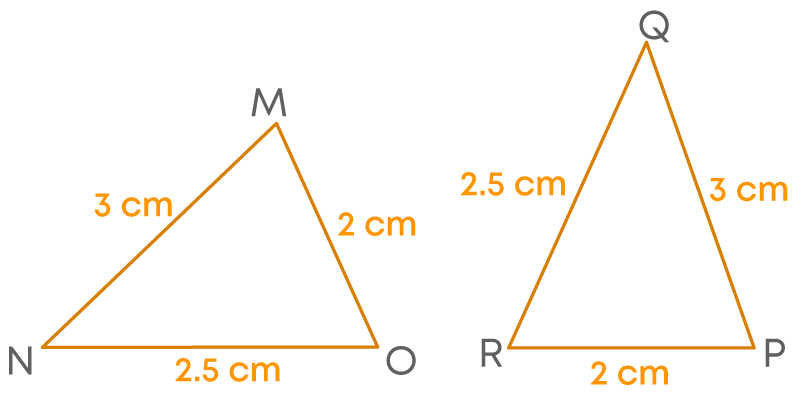
What do you mean by coinciding? When a figure is superimposed on the other, if they look like one figure, we say they are coinciding. Triangles MNO and PQR are congruent. Let us superimpose them.
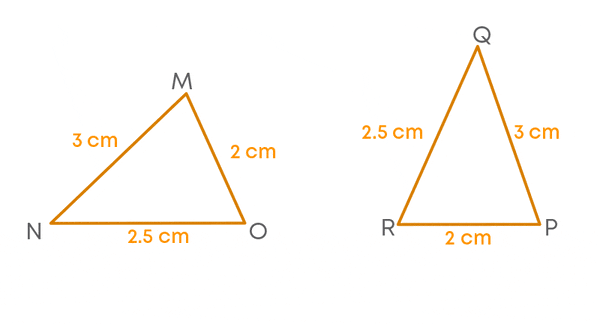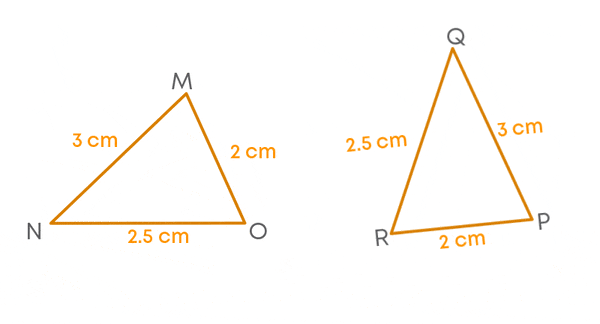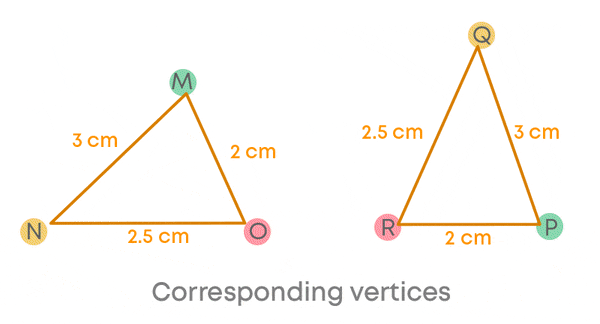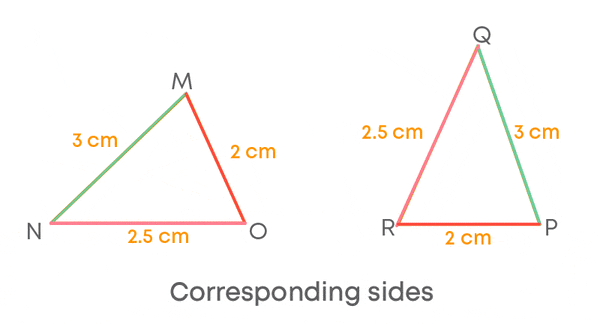
We can see that when triangles are superimposed, ∠M coincides with ∠P, ∠N with ∠Q, and ∠O with ∠R.
We know that the corresponding parts of congruent triangles are equal. So, here
- ∠M = ∠P
- ∠N = ∠Q
- ∠O = ∠R
i.e., the angles which coincide are equal.
In general, we can say that if two things coincide, they are equal. Euclid stated this fact in the form of an axiom as “Things which coincide with one another are equal”. Also, we can say two things are coinciding, when one thing can be substituted with the other.
Though this axiom sounds more related to geometry, it is mainly used while solving equations (in algebra as well as geometry) in the form of substitution.

The Whole Is Greater Than The Part
Consider a cake. It is cut and a piece is taken out.

Now, there are two parts of the cake. Are these two parts smaller than the whole cake? Definitely! This is obvious. Parts of a cake are always smaller than the whole cake. In other words, the whole cake is bigger than its cut parts.
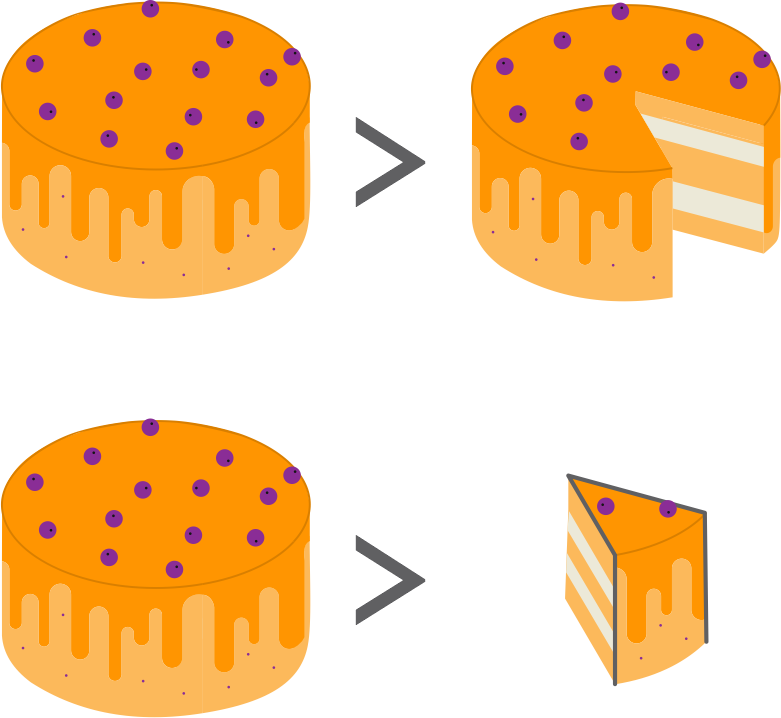
In general, we can say that a whole thing is always bigger (greater) than its parts. Euclid stated this obvious fact in the form of an axiom as “Whole is greater than the part”. This axiom is used in many mathematical proofs, especially in geometry.

Things Which Are Double Of The Same Thing Are Equal To One Another
Consider a quarter of a circle.

What will the double of a quarter of a circle give?

It is a semi-circle. A semi-circle is a half of the circle. All semi-circles of the same circle are equal. Thus, the doubles of a quarter of a circle are equal.
In general, we can say that the doubles of the same thing are equal to one another.
Euclid stated this obvious fact in the form of an axiom as “Things which are double of the same thing are equal to one another”. This axiom is mainly used while solving mathematical equations.
For example, consider the equation x 2 = 5
To solve this, let us take the double of the terms on the LHS and the RHS.
2 × x 2 = 2 × 5
We get x = 10 by using the axiom ‘things which are double of the same thing are equal to one another.’

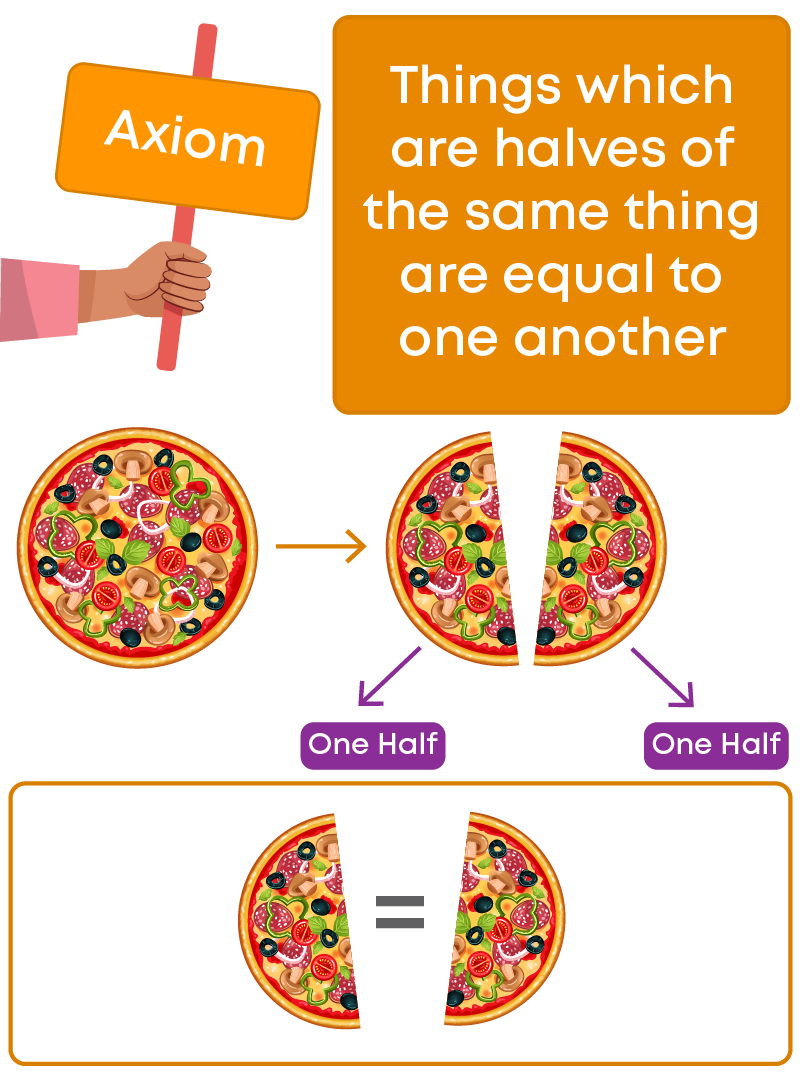
Things Which Are Halves Of The Same Thing Are Equal
Take a square sheet of paper. Fold it in half.

We can see that the two halves of the square sheet coincide. We have already discussed the axiom “Things which coincide with one another are equal”. So, the two halves are equal.
Here, the two halves are of the same square and they are equal. Let us look at one more example.
Consider a rectangle of the dimensions 4 cm and 6 cm.

What is the area of the rectangle? Area = 4 cm × 6 cm = 24 cm2
Now, let us cut it into half. How do you cut a rectangle into halves? You can try different ways using a rectangular sheet. There are 4 ways to cut it into half, as shown below.
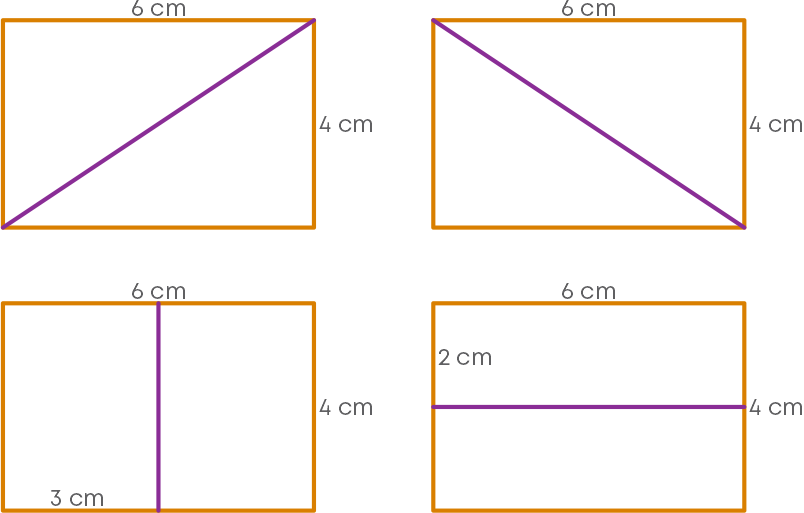
Let us calculate the area of each half of the rectangle.
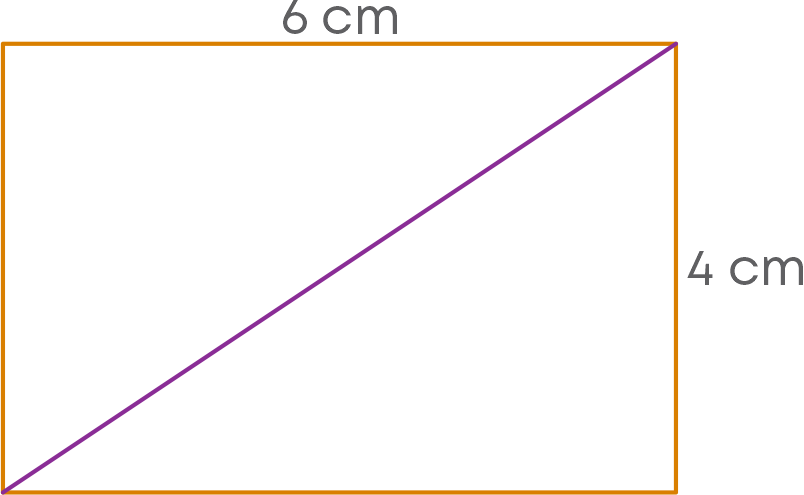
Area A1 = 1 2 × 4 cm × 6 cm = 12 cm2
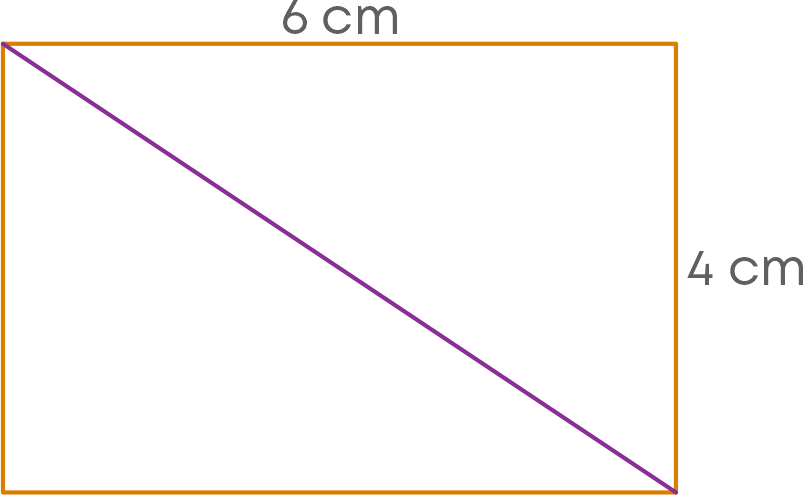
Area A2 = 1 2 × 4 cm × 6 cm = 12 cm2

Area A3 = 3 cm × 4 cm = 12 cm2
What do you observe? All the areas are equal. So, here we can say that the halves of the same rectangle are equal.
In general, we can say that the halves of the same thing are equal to one another.
Euclid stated this obvious fact in the form of an axiom as “Things which are halves of the same thing are equal to one another”.
Mathematically, we can express it as shown below:
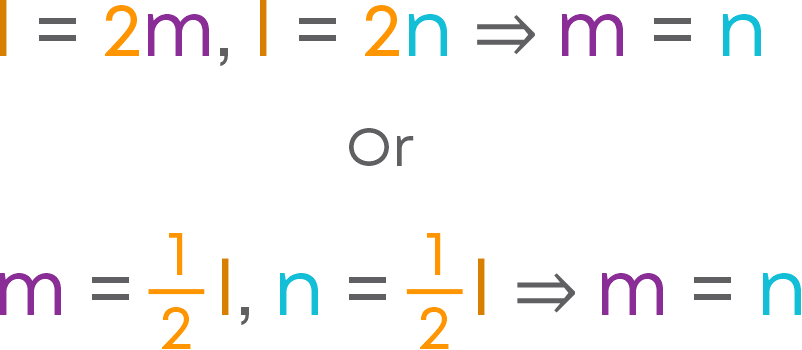
This axiom is mainly used while solving mathematical equations.
Euclid’s Five Postulates
We have already learnt about axioms. Also, we have gone through some of the axioms and their applications.
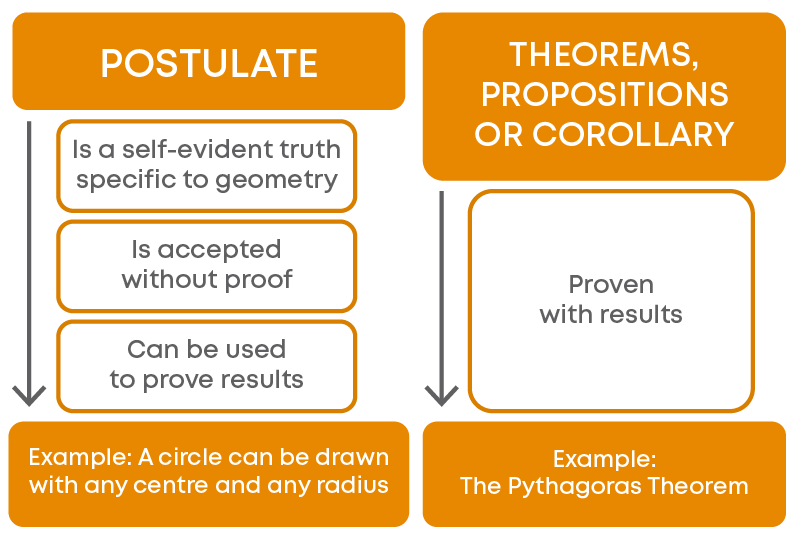
Euclid assumed certain properties, which were not to be proved. These assumptions are actually ‘obvious universal truths’.
- He divided them into two types: axioms and postulates.
- He used the term ‘postulate’ for the assumptions that were specific to geometry.
- Axioms, on the other hand, were assumptions used throughout mathematics and not specifically linked to geometry.
So, a postulate is a self-evident truth specific to geometry. As we use axioms to prove results, postulates are also used to prove some results in geometry.
Proven results are called theorems, propositions, or corollary.

Postulate 1
Euclid’s postulate 1 states that a straight line may be drawn from any point to any other point. Infinitely many lines can be drawn through a point. Only one line can be drawn through two given points.

In Euclidean geometry, we know that a line segment is the shortest curve joining two points (which are endpoints of the line segment).
In spherical geometry, the lines of minimum length joining two points on a spherical surface are called geodesics.
In Euclidean geometry, parallel lines never meet. Is it the same in spherical geometry too?

On a sphere, two parallel lines eventually meet. This means that since the Earth is spherical, Euclidean geometry is insufficient for studying it. We cannot create a perfect map representation of the Earth, on a flat surface. To represent the entire surface of the earth without any kind of distortion, we use a spherical map which is known as a globe.

Since a globe is not a practical map for showing a great amount of detail for a small region, flat maps are created and used.
The models that may be selected in preparing a flat map of the earth are known as projections. A flat map does not show a true shape for all regions and has cumulative measurement errors.
The spherical coordinates of a globe use a measurement grid composed of meridians of longitude and parallels of latitude.
Postulate 2
What we now call a line segment, Euclid had called a terminated line. We know that a line segment is a part of a line.

Line segment AB is a part of the line ‘l’. In the words of Euclid, AB is a terminated line.
You can observe here, if the line segment AB is extended endlessly beyond its endpoints, we get the line ‘l’.

Euclid has stated this as postulate 2: a terminated line can be produced indefinitely. In other words, a line segment can be extended on both sides to form a line.
Postulate 3
Euclid's Postulate 3 states that a circle can be drawn with any centre and any radius. Two or more circles with the same centre and different radii can be drawn.
If you wish to travel from one place to another in a private vehicle like a cab or your own car, what do you use to find the route? Maps on phone which use GPS.
What is GPS?
The Global Positioning System (GPS) utilizes latitude and longitude to tell its user where they are on the earth. GPS does not calculate its coordinates in a spherical coordinate system but calculates in a Cartesian coordinate system with the origin found at the centre of the earth.
GPS is a satellite-based navigation system. It provides positioning, velocity, and time information.
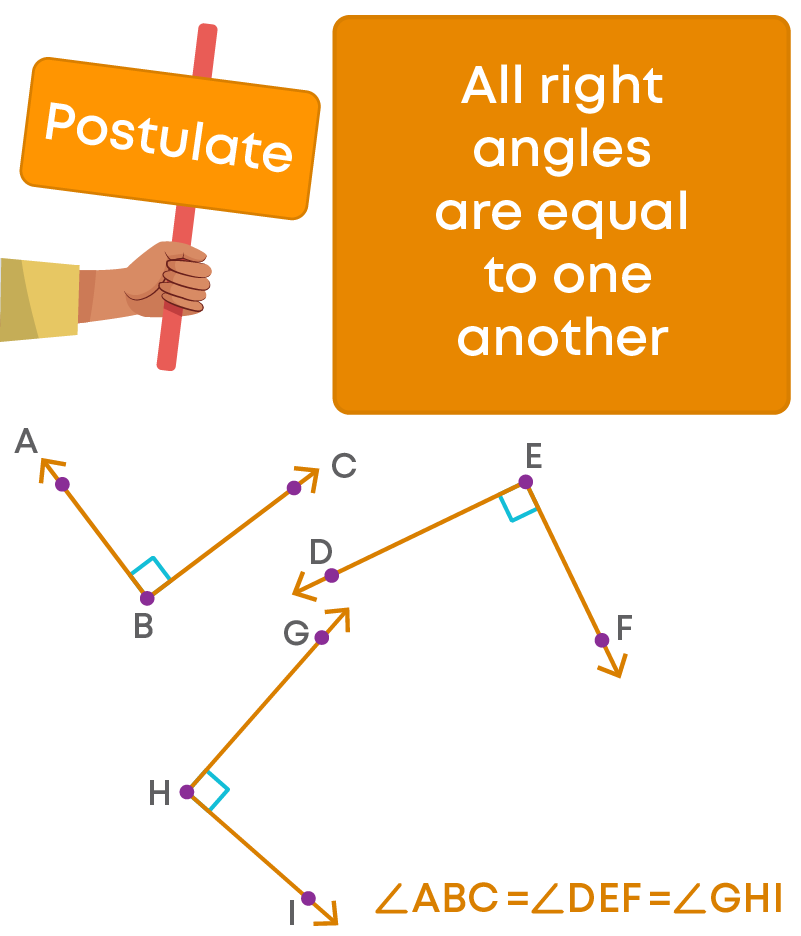
Postulate 4
Consider the two right angles given below.

Let us try to superimpose them.
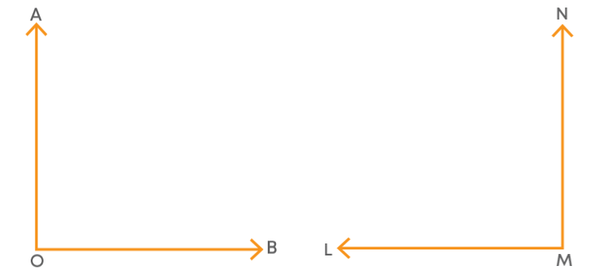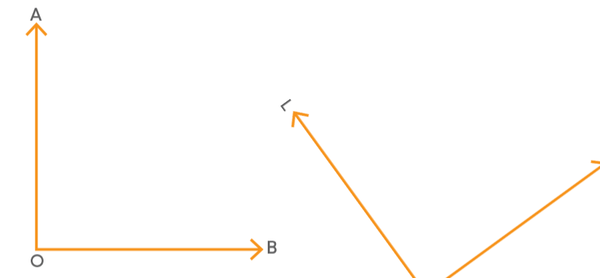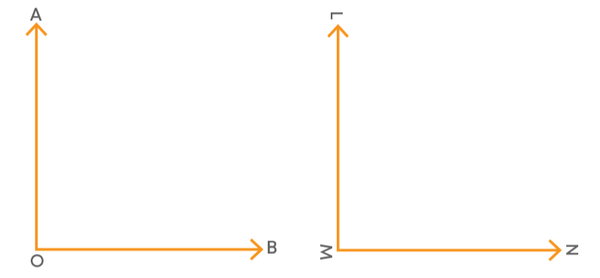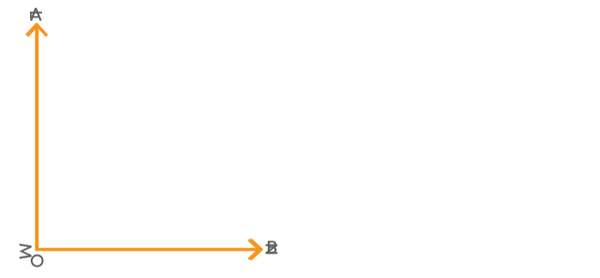
We can see that the two angles coincide when they are superimposed. Earlier in this chapter, we discussed the axiom “Things which coincide are equal to one another”. So, since here the two angles coincide, we can say that they are equal.
i.e., right angles are equal.
Euclid stated this in the form of a postulate as “All right angles are equal to one another”.
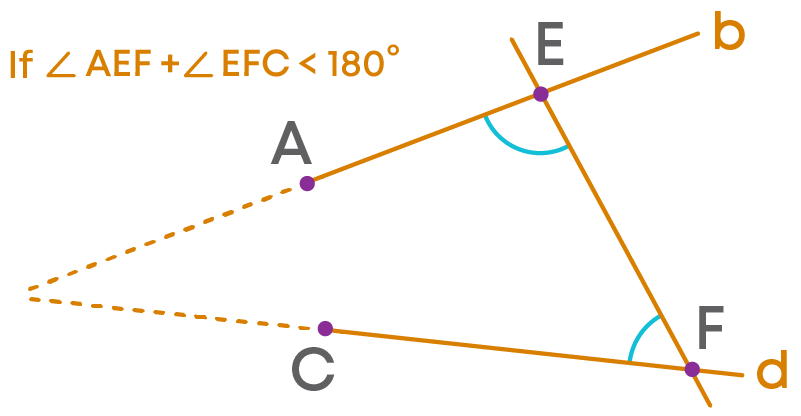
Postulate 5
We know that if the pair of lines are parallel, the sum of the interior angles on the same side of the transversal sum up to 180⁰.
What if the lines are not parallel? Let us consider an example.

Consider the lines AB and CD which are not parallel. Since they are not parallel, they will meet at a point. But we do not know where they meet. By extending the lines we can find where they meet.
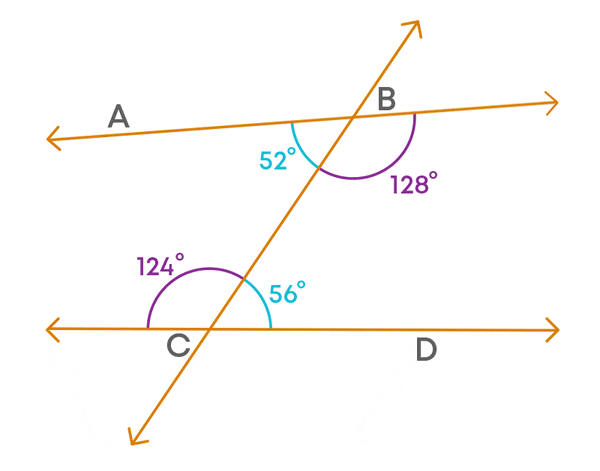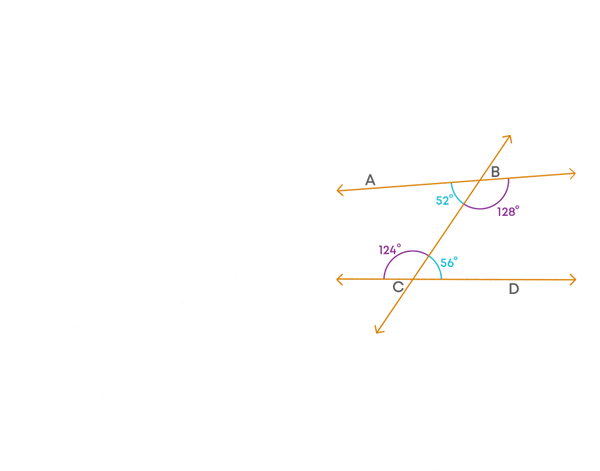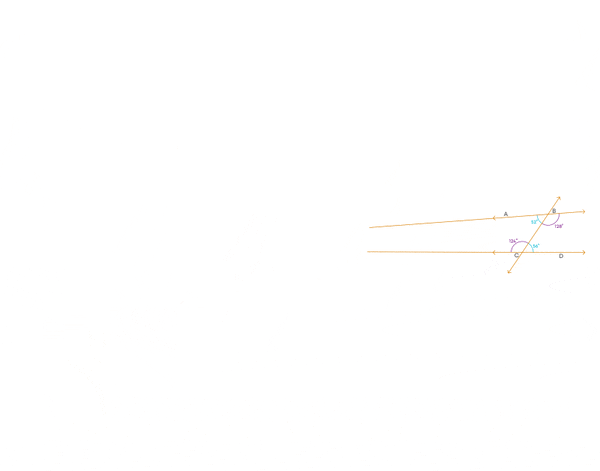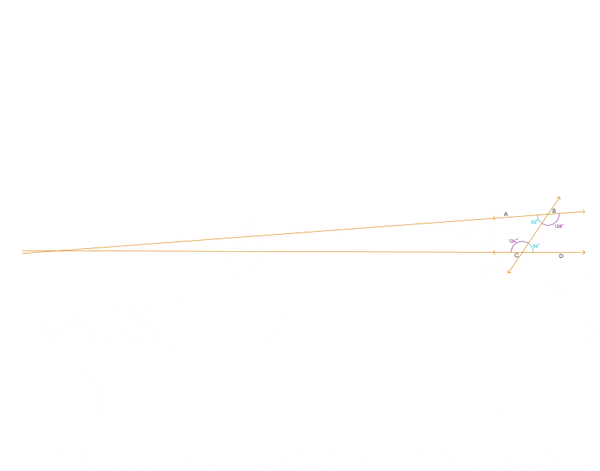
We can find that the two lines meet by extending on the left side of the transversal. Now, we will check the sum of the interior angles formed on the left side of the transversal. The angles are 52⁰ and 124⁰.
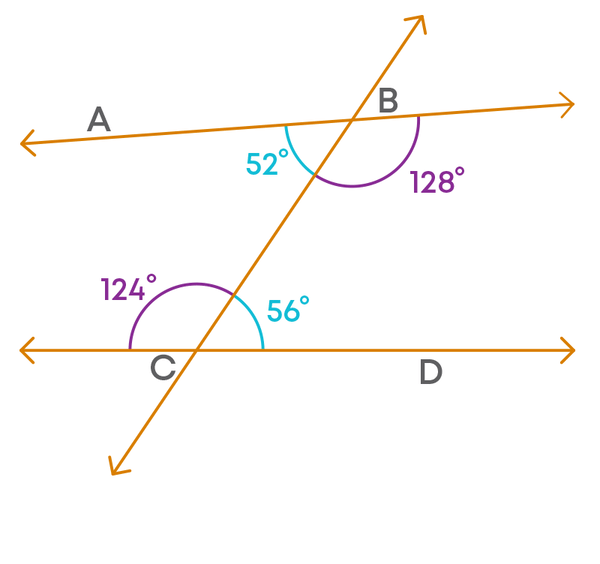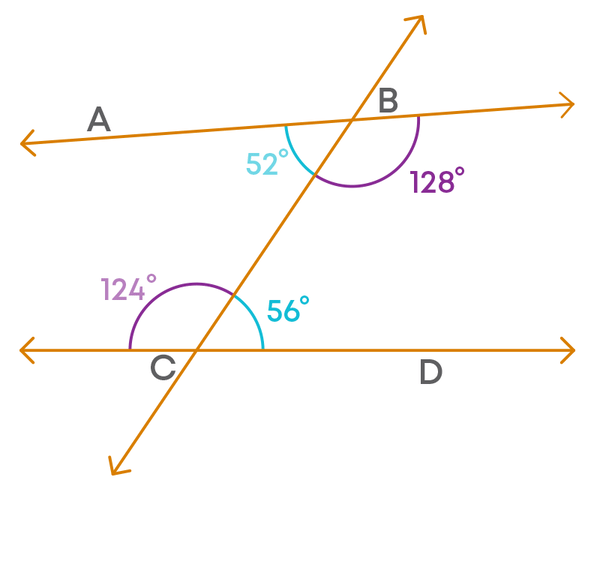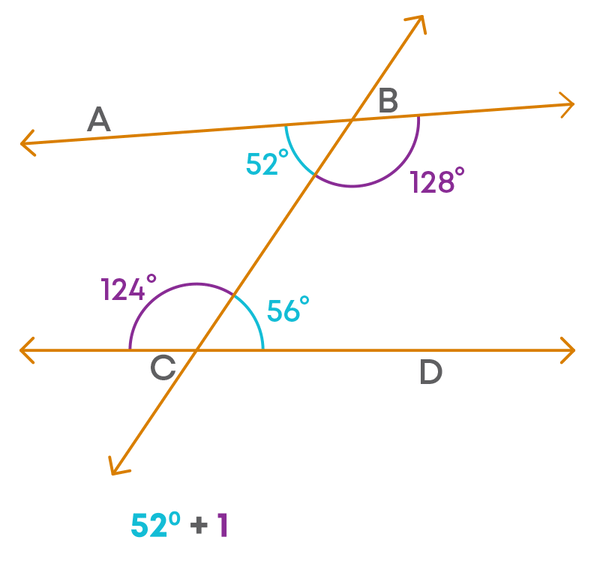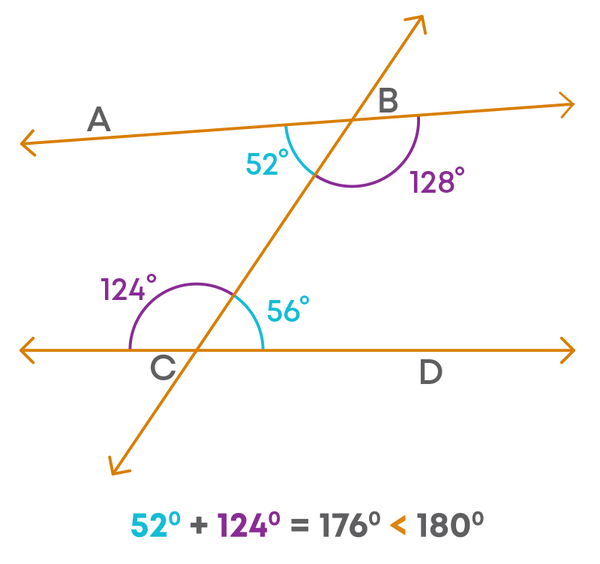
The sum of the interior angles on the left side of the transversal is less than 180⁰.
What about the sum of the interior angles on the right side of the transversal?
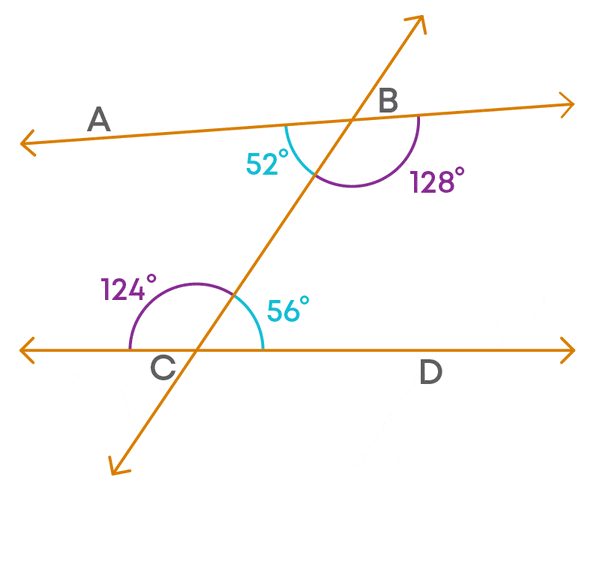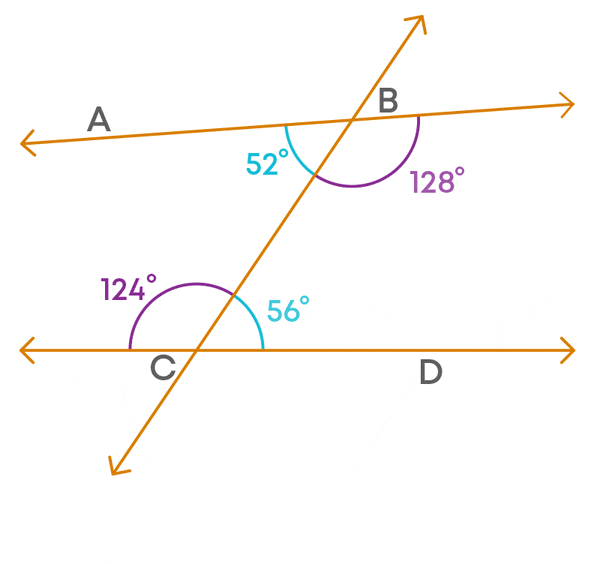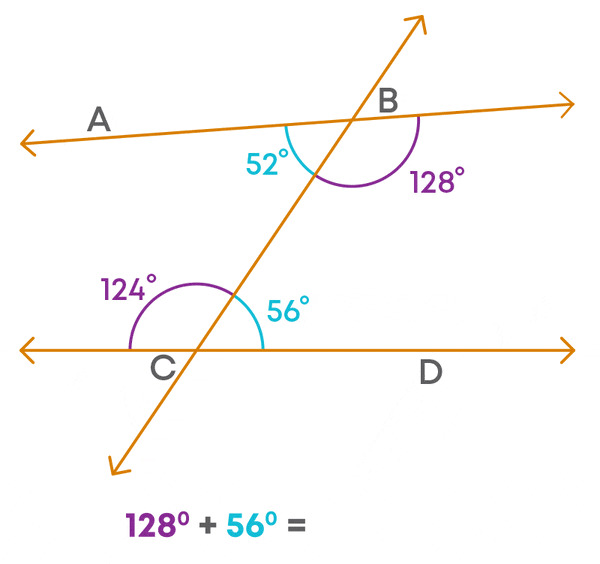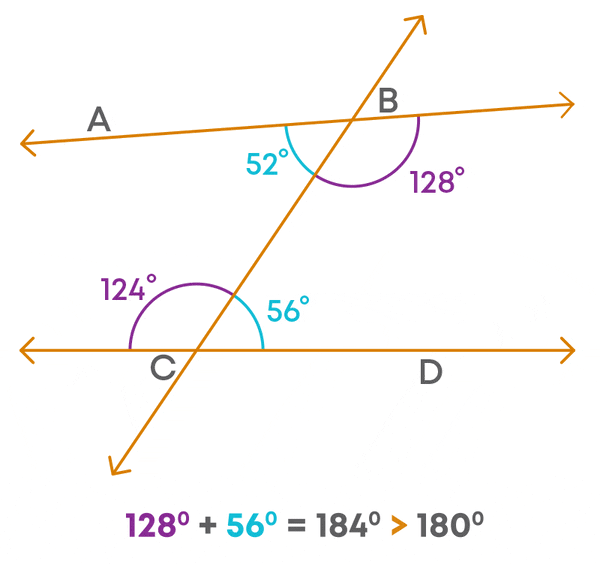
The sum of the interior angles on the right side of the transversal is greater than 180⁰.
We should note here that the lines meet on the left side of the transversal and the sum of the interior angles on the left side of the transversal is less than 180⁰.
So, we can say in general that two lines meet on that side on which the sum of the interior angles formed by a transversal with the two lines is less than 180⁰ (or two right angles).
Euclid stated this in the form of a postulate as
“If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles”.
Nowadays, ‘postulates’ and ‘axioms’ are terms that are used interchangeably and in the same sense. ‘Postulate’ is actually a verb. When we say, “let us postulate”, we mean, “let us make some statement based on the observed phenomenon in the Universe”. Its truth/validity is checked afterwards. If it is true, then it is accepted as a ‘Postulate’.
A system of axioms is called consistent, if it is impossible to deduce from these axioms a statement that contradicts an axiom or previously proved statement.
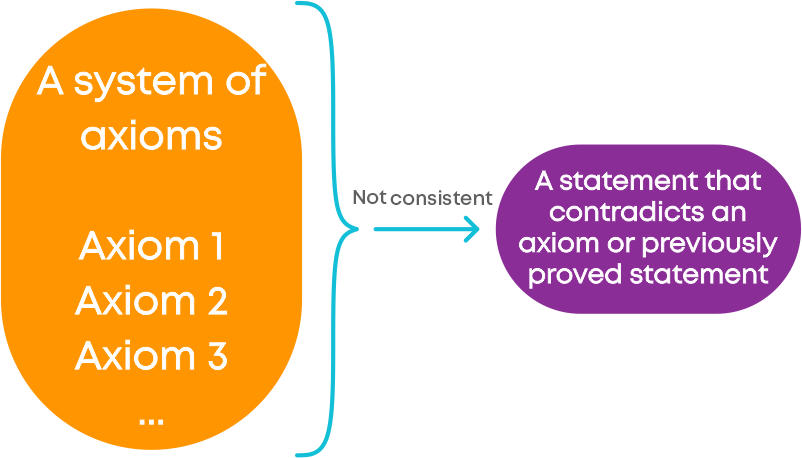
So, when any system of axioms is given, it needs to be ensured that the system is consistent. After Euclid stated his postulates and axioms, he used them to prove other results.
Then using these results, he proved some more results by applying deductive reasoning.
- A sentence which can be judged to be true or false is called a statement.
E.g.,

- The statements that were proved are called propositions or theorems. Establishing the truth of a theorem is called proving the theorem.
- A statement whose truth can be easily deduced from a theorem is called its corollary.
Euclid deduced 465 propositions in a logical chain using his axioms, postulates, definitions, and theorems proved earlier in the chain.
Equivalent Versions of Euclid’s Fifth Postulate
There are several equivalent versions of Euclid’s fifth postulate. One of them is ‘Playfair’s Axiom’.
It states, “For every line ‘l’ and for every point P not lying on ‘l’, there exists a unique line ‘m’ passing through P and parallel to l”.

This can also be stated as the following:
Two distinct intersecting lines cannot be parallel to the same line.
Hyperbolic Geometry
The hyperbolic plane is a plane where every point is a saddle point.
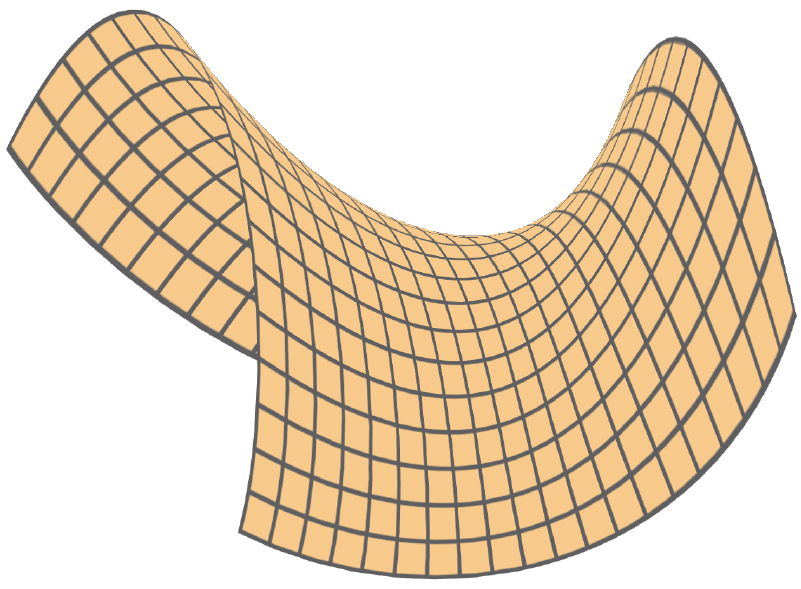
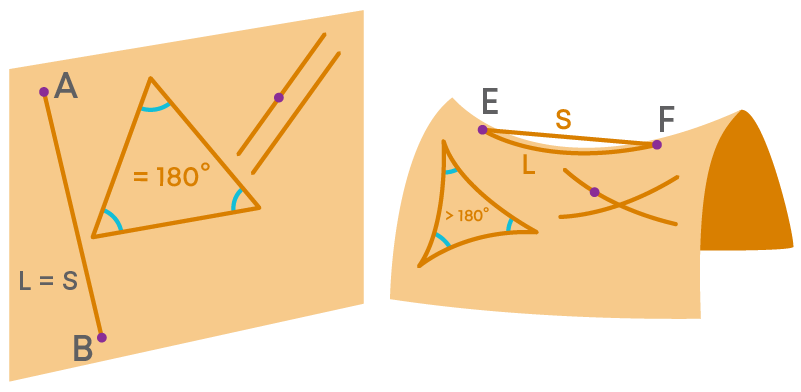
Hyperbolic geometry is more closely related to Euclidean geometry. Hyperbolic geometry is a geometry for which we accept Euclid’s first four postulates but not the fifth postulate.
- Properties of lines in hyperbolic geometry are the same as those of single straight lines in Euclidean geometry.
- Properties of two intersecting lines are the same as those of two intersecting lines in Euclidean geometry. For example, two distinct intersecting lines can have only one point in common.
- When we talk about more than two intersecting lines, then there can be properties of intersecting lines in Hyperbolic geometry that differ from intersecting lines in Euclidean geometry.
- Parallel lines also have properties that differ from parallel lines in Euclidean geometry.
Common Errors
The following are topics in which students make common mistakes when dealing with Euclid’s geometry:
- 1. A point
- 2. When equals are subtracted from equals, the remainders are equal
- 3. A terminated line can be produced indefinitely
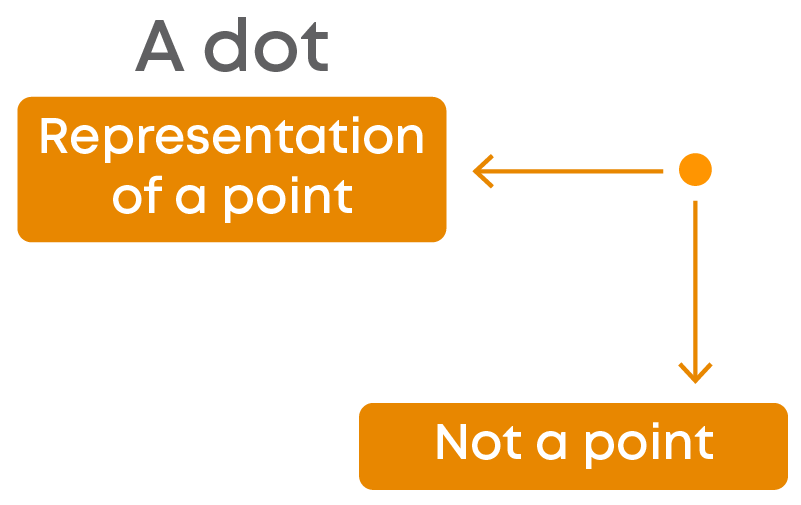
A Point
A dot marked on a sheet of paper is not exactly a point. It is just the representation of a point. In fact, a point does not have a dimension. But a dot marked on paper has some dimension.

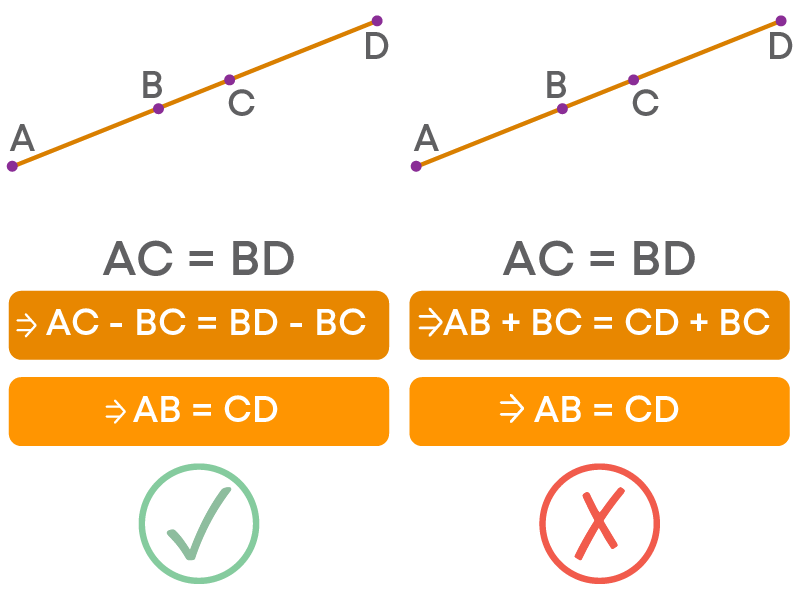
When Equals Are Subtracted From Equals, The Remainders Are Equal
If AC = BD, to prove AB = CD, we use the axiom “If equals are subtracted from equals, the remainders are equal”.
A Terminated Line Can Be Produced Indefinitely
A terminated line can be produced indefinitely. This is a postulate, but not a definition.
Conclusion
Now that you have learnt about Euclid’s geometry, can you solve this puzzle?
Choose words related to Euclid’s geometry which appear in the grid below:





















































